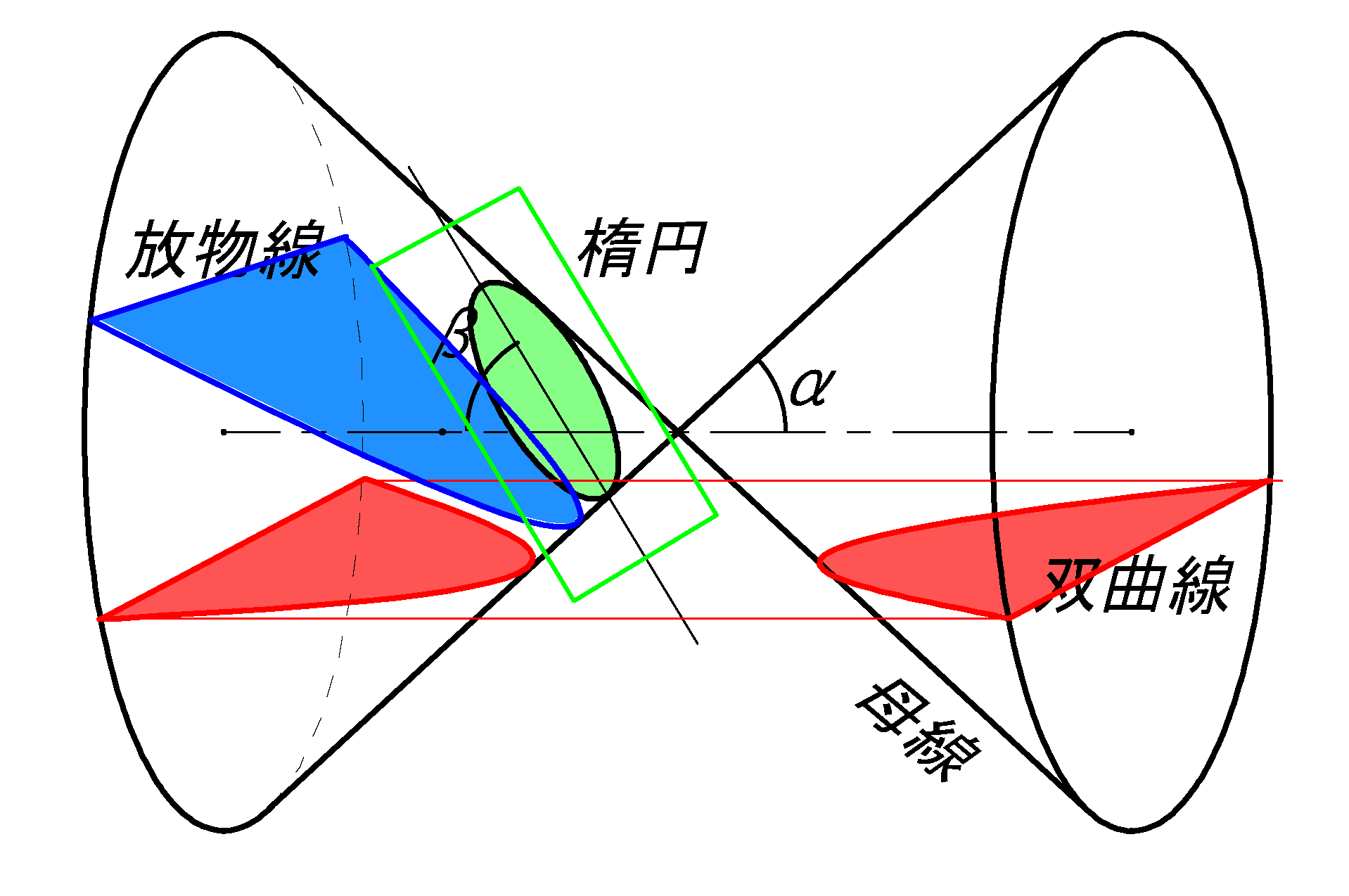
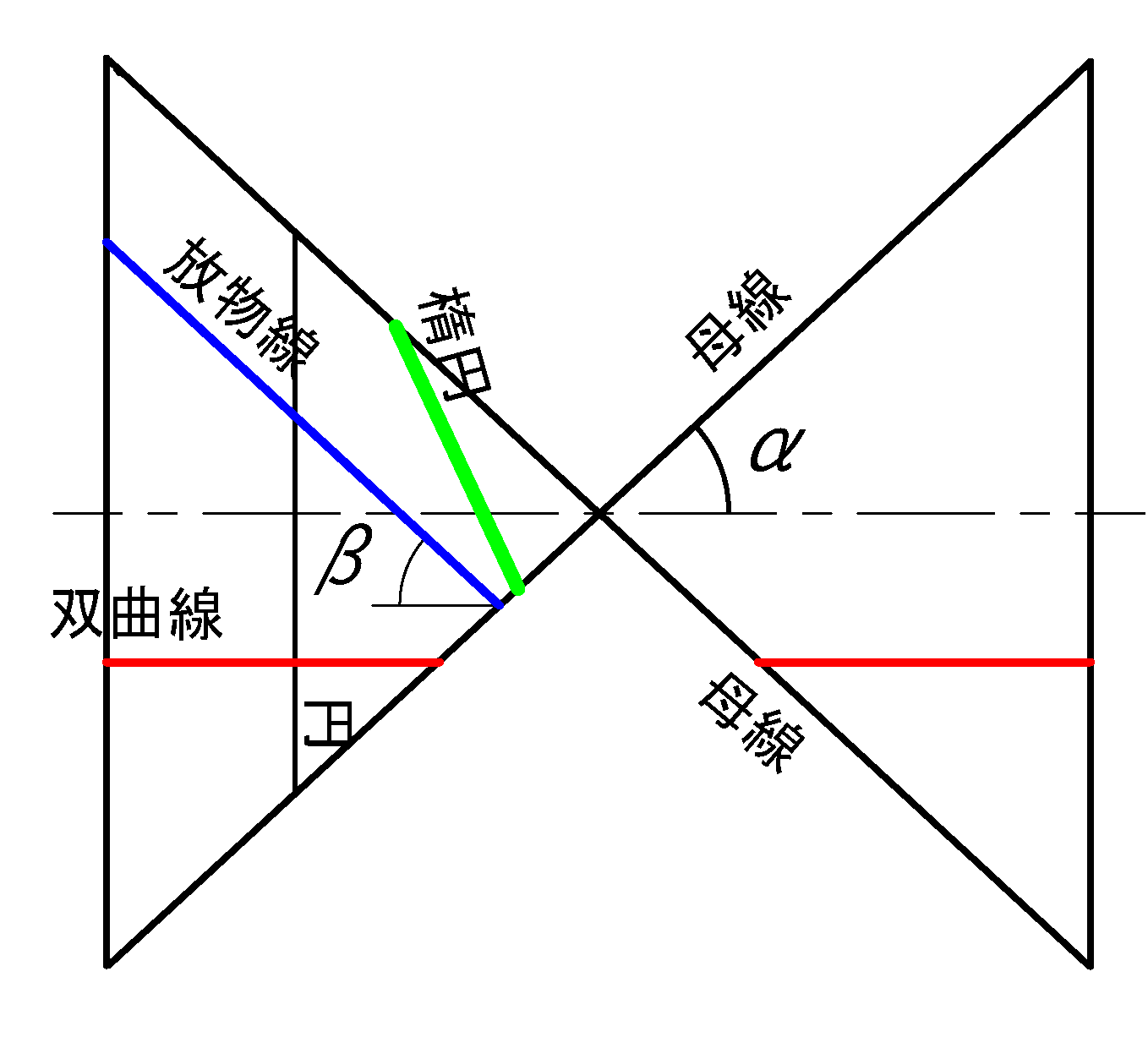
媒介変数表示(パラメータ)のメリットは 一つの変数\(θ\) により2つの変数x とy 個別に決まることです。
円の場合と比較して考えてみる。
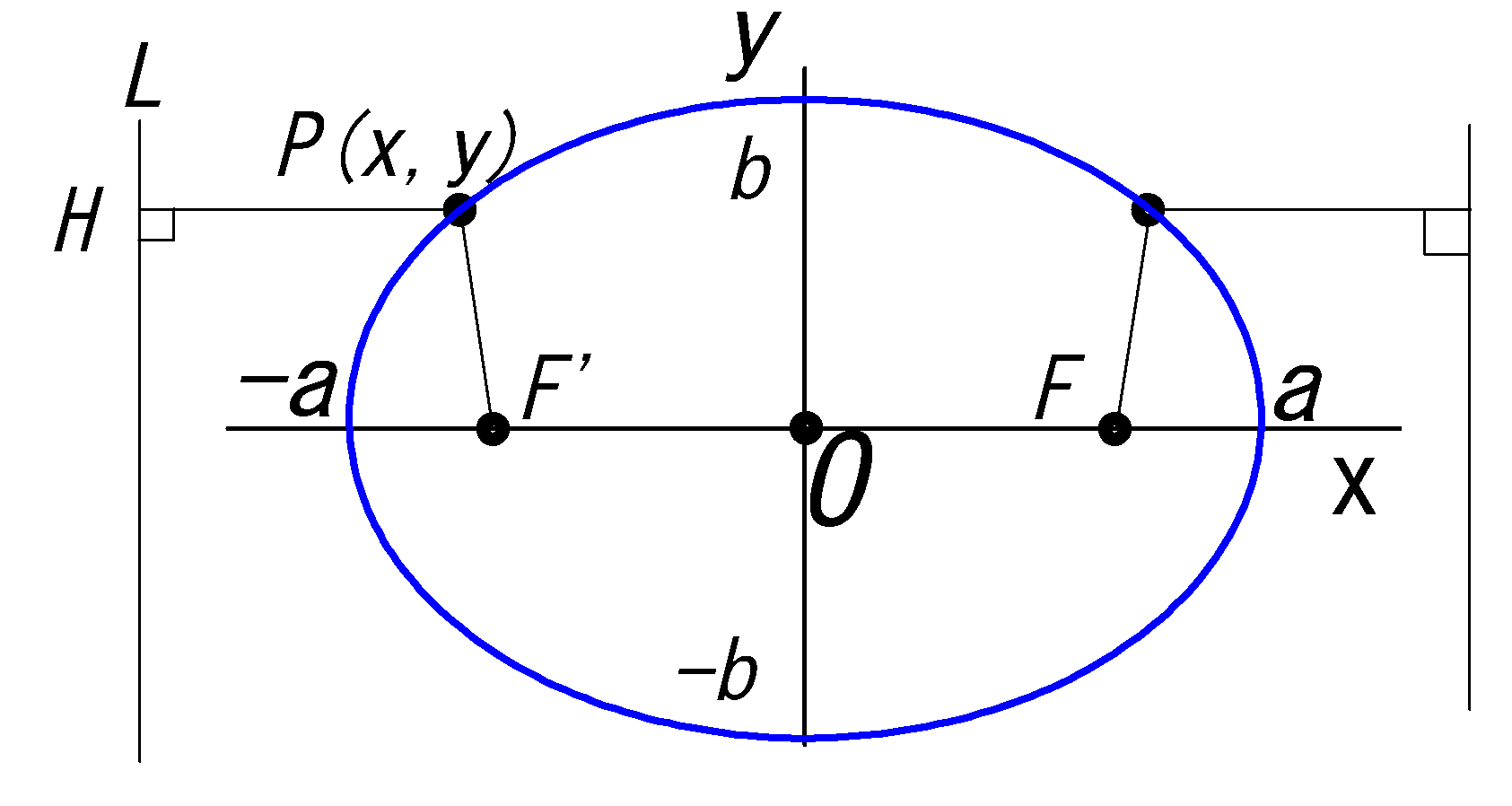
円 \(x^2+y^2=r^2\)の媒介変数表示は:
\(x=rcosθ\) \(\ , \ \) \(y=rsinθ\)である。
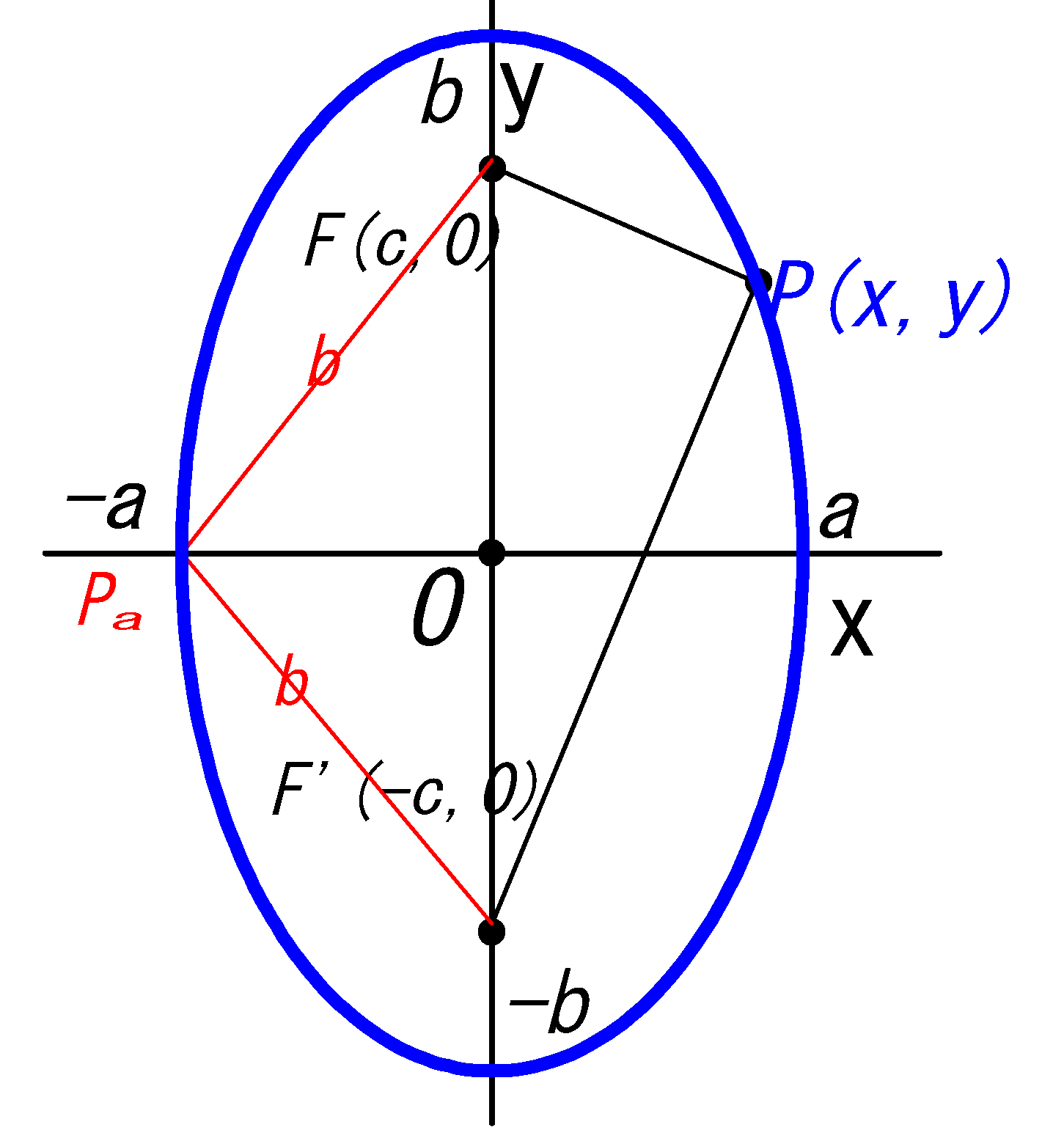
•楕円\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) の媒介変数表示は:
x成分は円と同じ、y成分は円に対して\(\frac{b}{a}\)倍 (縮む) となる。すなわち
\(\color{blue}{x=acosθ}\)\(\ , \ \)\(\color{blue}{y}=\frac{b}{a}(a sinθ)\) \(\color{blue}{=bsinθ}\)
\(\ :❺\)
•\(\frac{(x-d)^2}{a^2}+\frac{(y-e)^2}{b^2}=1\) の媒介変数表示は:
\(\color{blue}{x=acosθ+d}\) \(\ , \ \) \(\color{blue}{y=bsinθ+e}\) \(\ :❺'\)
\(t=tan \frac{θ}{2}\) \( (-\pi \lt \frac{θ}{2}\lt \pi)\)とすると、 次のcosθ, sinθ が得られる。
(少し大変ですが、興味ある方のリンク先⇒
【参照先】です。)
\(cosθ=\frac{1-t^2}{1+t^2}\) \(\ , \ \) \(sinθ=\frac{2t}{1+t^2}\)
これより
\(\color{blue}{x=acosθ=\dsfr{a(1-t^2)}{1+t^2}}\) \(\ , \ \) \(\color{blue}{y=bsinθ=\dsfr{2bt}{1+t^2}}\)
グラフを描くときの注意:
・t は\(t=tan \frac{θ}{2}\)から求める。
・θ は\( (-\pi \lt \frac{θ}{2}\lt \pi)\) (\(\frac{\pi}{2}\)を除く領域)
平方完成
【参照先】を使い楕円の標準形の式に変形する。
\(4(x^2-4x)+9(y^2-2y)-11=0\)
\(4(x-2)^2-16+9(y-1)^2-9-11=0\)
\(4(x-2)^2+9(y-1)^2-36=0\)
\(4(x-2)^2+9(y-1)^2=36\)
\(\frac{(x-d)^2}{a^2}+\frac{(y-e)^2}{b^2}=1\)の形にする
\(\frac{4(x-2)^2}{36}+\frac{9(y-1)^2}{36}=1\)
\(\frac{(x-2)^2}{9}+\frac{(y-1)^2}{4}=1\)
\(\therefore \dsfr{(x-2)^2}{3^2}+\dsfr{(y-1)^2}{2^2}=1\)
•中心:\((2,1)\) •長軸長:\(2a=2\cdot 3=6\) •短軸長:\(2b=2\cdot 2=4\)
式❸より\(c=\sqrt{a^2-b^2}=\sqrt{3^2-2^2}=\sqrt{5}\)
•焦点:\( (\pm\sqrt{5},\ 0)\)\(≒(\pm 2.23,\ 0)\)
上記で求めた中心、長軸、短軸からフリーハンドでおおよそなグラフは描ける。
今回は媒介変数を使い\((x,y)\)座標を求めて、各点をプロットしました。
式❺'より
\( \color{blue}{x=acosθ+d}\)\(=3cosθ+2\)
\( \color{blue}{y=bsinθ+e}\)\(=2sinθ+1\)
この式をエクセルに入れて、グラフにしたのが下図です。
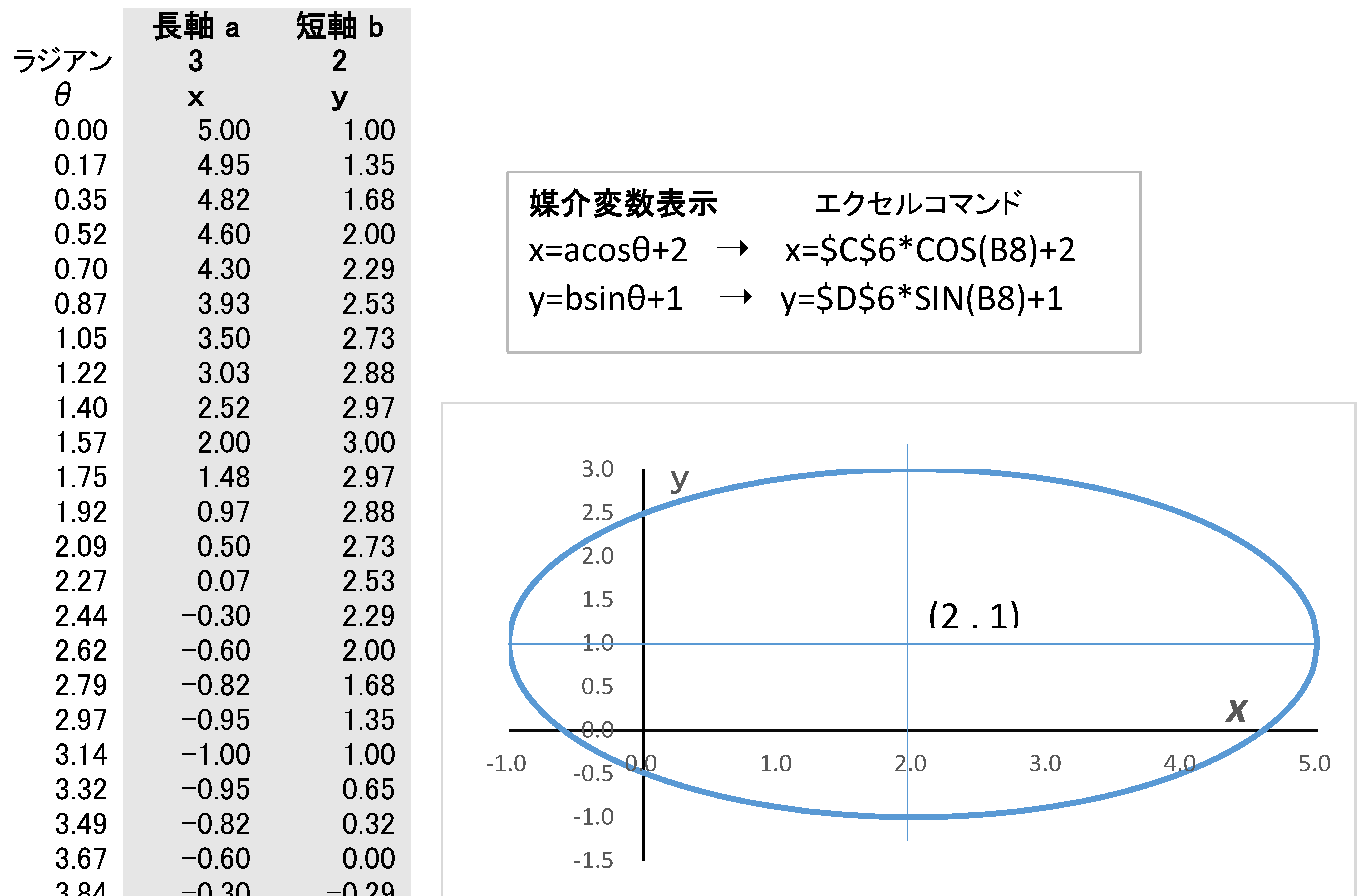
fig7 \(\frac{(x-2)^2}{3^2}+\frac{(y-1)^2}{2^2}=1\)
長軸、短軸の長さを\(a,\ b\)とし、楕円の面積\(S\) は:
\(S=ab\pi\) \(\ :❻\)
単位円(半径=1)の面積\(\pi\) の\(ab\) 倍とすると覚えやすい。
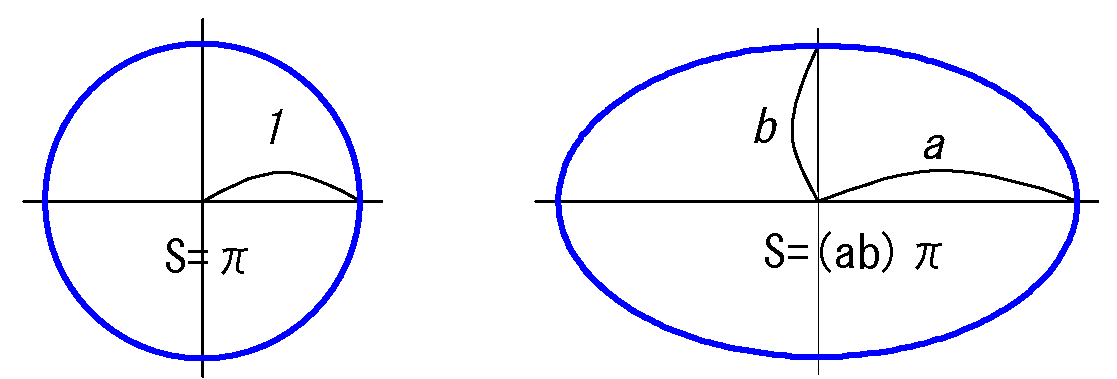
fig8 面積のイメージ
公式❻ の導出は積分により求めるのがよい。
これを大まかに言うと:
\( \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\)から
\( y=b\sqrt{1-\frac{x^2}{a^2}}\)を得る。
この式の第1象限の面積(積分区間\([0,a]\)) を積分により求め、その4倍が楕円の面積である。
ここではこの程度にしますが、興味のある方のリンク先⇒
【参照先】です。
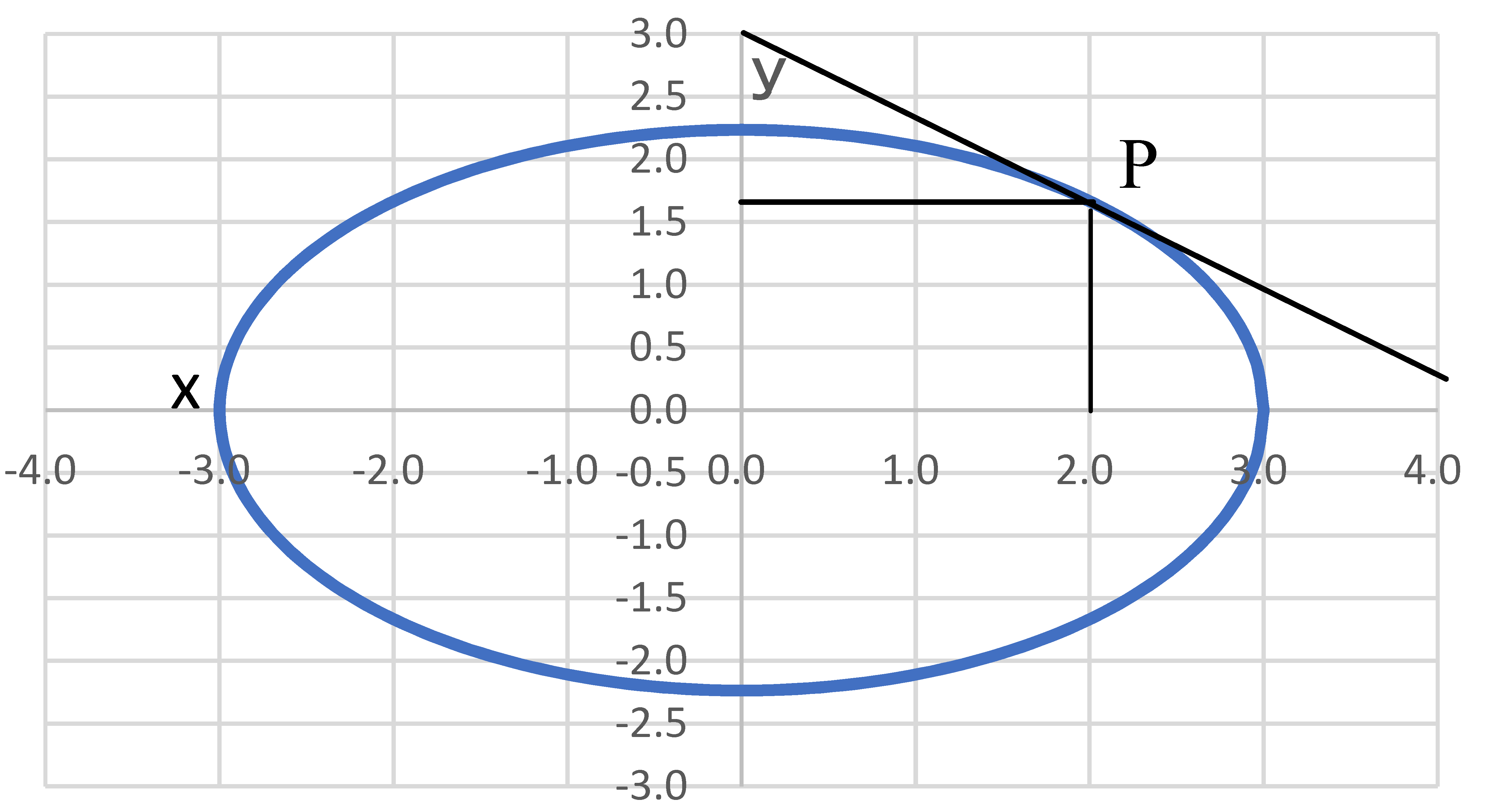
次式は楕円上の点\((x_1,y_1)\) における接線の方程式である。
\(\underline{\dsfr{x_1 x}{a^2}+\dsfr{y_1 y}{b^2}=1}\) \(\ :❼\)
この式の導出方法の中で、ここでは簡潔な方法として微分を使い説明していきます。
次式は曲線の\((x_1,y_1)\)における接線の方程式です:
【参照先】
\(y=m(x-x_1)+y_1\) \(\ \iff \ \) \(\color{blue}{y=f'(x_1)(x-x_1)+y_1}\) \(\ :ⓑ\)
\(\color{blue}{m=f'(x_1)=\der{y}{x}(x_1)}\)
・\(m\) は\(x_1\)における接線の傾きであり、この\(m\)は次の微分係数に等しい。
・\(f'(x_1)\)はy の微分に\(x_1\) を代入しもの…これを\(x_1\)における微分係数という
与式ⓐ の両辺をx で微分する:
以下の朱記の微分は合成関数の微分です:
\( \der{}{x}(\frac{y^2}{b^2})\)\(=\der{y}{x}\der{}{y}(\frac{y^2}{b^2})\) \(=\frac{2y}{b^2}\der{y}{x}\)
楕円の方程式は陰関数、少し特殊です、難解であれば、傾きの結果をそのまま受け入れて先に進みましょう。
・先に進む:【前 進】
・「合成関数の微分」:【参照先】
・「陰関数の微分」:【参照先】
\(\der{}{x}(\frac{x^2}{a^2}+\frac{y^2}{b^2})=\der{}{x}(1)\) \(\ \Rightarrow\)
\(\der{}{x}(\frac{x^2}{a^2})+\color{red}{ \der{}{x}(\frac{y^2}{b^2}) }=0\)\(\ \Rightarrow\)
\(\frac{2x}{a^2}+ \color{red}{\der{y}{x}\der{}{y}(\frac{y^2}{b^2})}=0\)\(\ \Rightarrow\)
\(\frac{2x}{a^2}+\color{red}{\frac{2y}{b^2}\der{y}{x} }=0\)\(\ \Rightarrow\)
\(\der{y}{x}=\frac{b^2}{2y}(-\frac{2x}{a^2})=\frac{-b^2x}{a^2y}\)
\((x_1,y_1)\)における傾きは:
\(\color{blue}{ m=f'(x_1)=\der{y}{x}(x_1)=\frac{-b^2x_1}{a^2y_1} }\)\(\ :ⓑ\)
これを式ⓑに代入
\(\color{blue}{ y=\dsfr{-b^2x_1}{a^2y_1}(x-x_1)+y_1 }\)
両辺 \(a^2 y_1\) をかけると
\(a^2 y_1 y=-b^2 x_1(x-x_1)+y_1 a^2 y_1\)\(\ \Rightarrow\)
\(a^2 y_1 y=-b^2 x_1 x + b^2 x_1^2 + a^2 y_1^2\)
\( b^2 x_1 x + a^2 y_1 y = \underline{ b^2 x_1^2 + a^2 y_1^2}\)\(\ :©\)
ところで,楕円の方程式に\(a^2 b^2\) 倍すると:
\(a^2 b^2 (\frac{{x_1}^2}{a^2}+\frac{{y_1}^1}{b^2})=a^2 b^2\)\(\ \Rightarrow\)
\(\color{black}{\underline{b^2 {x_1}^2 + a^2 {y_1}^2=a^2 b^2} }\)
だから式©は:
\(b^2 x_1x + a^2 y_1 y = \underline{a^2 b^2}\)
両辺に \(\frac{1}{a^2 b^2}\) を掛けると
\(\dsfr{x_1x}{a^2} + \dsfr{y_1 y}{b^2}=1\)
導出終わり
\(\frac{x^2}{3^2}+\frac{y^2}{(\sqrt{5})^5}=1\) \( \quad\) \(P(2, \frac{5}{3})\)