微分・導関数・微分可能性

∗微分の基本
 ∗微分係数の定義式
 ∗接線と法線の式
 ∗導関数の定義式
∗導関数の導出
 ∗\(x^n\)
 ∗\(sin\ x\)
 ∗\(cos\ x\)
 ∗\(tan\ x\)
∗微分可能性
∗なぜ開区間で微分可能なのか

上図においてx が a から a+h まで変化したときの f(x) の変化の度合い/程度、 すなわち、変化率を下式で表す。

\( \frac{f(a+h)-f(a)}{(a+h)-a}\)　\(=\frac{f(a+h)-f(a)}{h}\) \(= \frac{Δy}{Δx}\) \(\quad (1)\)

これを f(x) の平均変化率といい、直線 A－B1 の傾きを表している。

 次に図 fig2 を 参照をしながら、微分係数（※1）について説明を進めます。
今、点 a を固定して点 B1 を B2 に さらに B3 へ…と限りなく a に近付ける、このようにして h(= Δx)を 0 に近付けて極限をとる。
このことは平均変化率が f(x) の 点 A での接線の傾きに収束することです。

\( f'(a)=\displaystyle \lim_{ h \to 0} \frac{f(a+h)-f(a)}{h}\) \(\quad (2)\)
\( f'(a)=\displaystyle \lim_{ x \to a} \frac{f(x)-f(a)}{x-a}\) \(\quad (2)'\)

次のようにも表す

\( f'(a)=\frac{df}{dx}(a)=\frac{d}{dx}f(a)\)

注1:（※1）
微分係数に対応する関数を導関数という。また導関数を求めることを微分するという。
微分係数を求める手順の多くは「➀関数の導関数を求め　②求めた導関数から微分係数を求める」です。

接線と法線の方程式
微分係数から曲線に接線、法線が求まる
曲線の点 \((a,b)\) における接線の式：

\(y-f(a)=f'(a)(x-a)\)
\(y=f'(a)(x-a)+b\) \( \quad (b=f(a))\)

曲線の点 \((a,b)\) における法線の式：

\(y-f(a)=-\frac{1}{f'(a)}(x-a)\)
\(y=-\frac{1}{f'(a)}(x-a)+b\)

接線と法線の傾きの積

\(f'(a) \x (-\frac{1}{f'(a)})=-1\)

 微分係数に対応する関数であり、微分係数の定数 a を変数 x に置き換えた式です。
導関数の変数 x に定数を入力すれば微分係数が出力される。

\( f'(x)=\displaystyle \lim_{ h \to 0} \frac{f(x+h)-f(x)}{h}\) \(\quad (3)\)

\( (x+h)^n \) の展開なので 2項定理を使う。
（2項定理は 2 つ項の n 乗の式を展開する式）

\( f'(x)=\displaystyle \lim_{ h \to 0} \frac{f(a+h)-f(a)}{h}\) \( = \displaystyle \lim_{ h \to 0} \frac{1}{h} ((x+h)^n -x^2 \)

\( = \displaystyle \lim_{ h \to 0} \frac{1}{h} \) \( \left[ ( \displaystyle \sum_{ r = 0 }^{ n } {}_n \mathrm{ C }_r \ x^{n-r} \ h^r ) - x^2 \right] \)

\( = \displaystyle \lim_{ h \to 0} \frac{1}{h} \) \( [ \) \( ( \) \({}_n \mathrm{ C }_0 x^{n} + \underline{ {}_n \mathrm{ C }_1 x^{n-1} h } \) \(\cdots + {}_n \mathrm{ C }_r x^{n-r} h^r\) \(\cdots+ {}_n \mathrm{ C }_{n-1} x h^{n-1}+{}_n \mathrm{ C }_n h^n \) \( )- x^2\) \( ] \)

\( = \displaystyle \lim_{ h \to 0} \frac{1}{h} \) \( [ \) \( ( \) \( \cancel{ x^{n} } + \underline{n\ x^{n-1} h } \) \(\cdots + \frac{n!}{r!(n-r)!}x^{n-r} h^r\) \(\cdots+ x h^{n-1}+ h^n \) \( )- \cancel{ x^2 }\) \( ] \)

\( = \displaystyle \lim_{ h \to 0} \) \( [ \) \( \underline{n\ x^{n-1} } \) \(\cdots + \frac{n!}{r!(n-r)!}x^{n-r} h^{r-1} \) \(\cdots+ x h^{n-2}+ h^{n-1} \) \( ] \)

\( \therefore f'(x) =\underline{ n\ x^{n-1} }\)

\(x^n\) の項はキャンセルされ「0」、下線以外の項は「0」となり、頻繁に使う微分公式が導出できました。

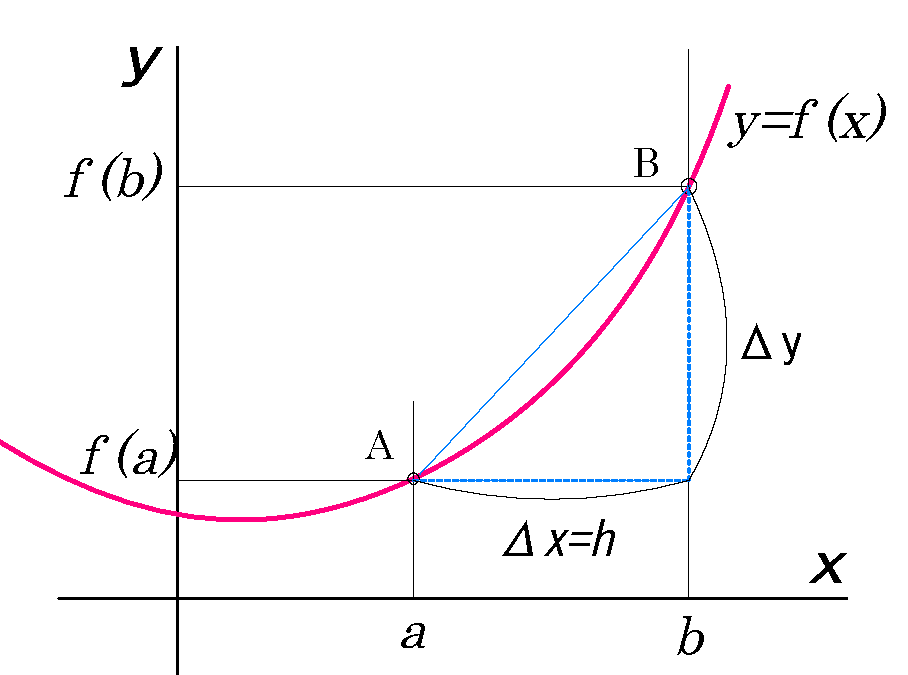
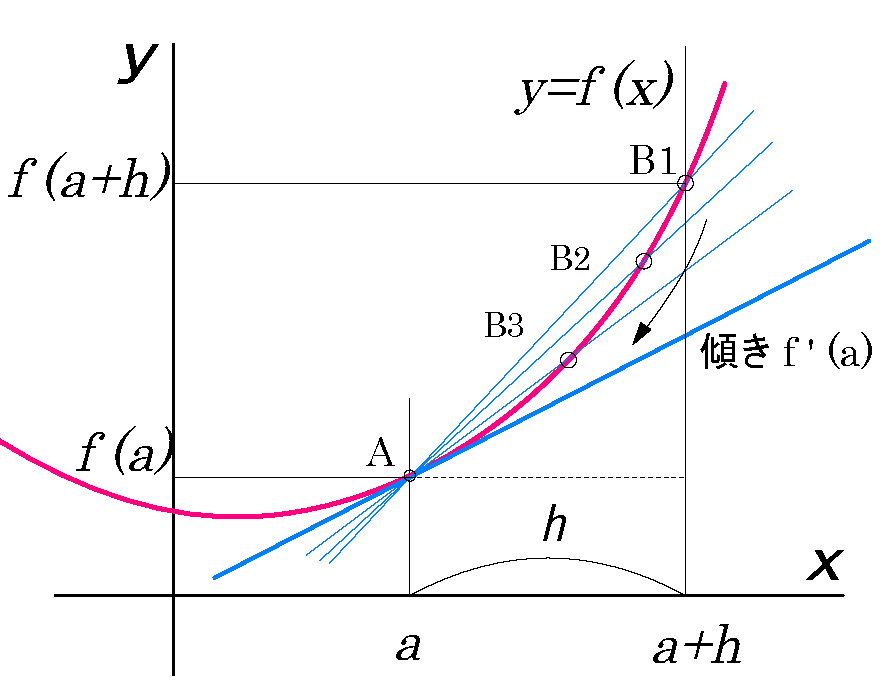
導出には次の式を使う。

➀ \( sinα-sinβ=2cos \frac{α+β}{2} sin\frac{α-β}{2} \) 【参考先】

➀\( \displaystyle \lim_{ x \to 0} \frac{sin\ x}{x}=1 \)
証明なしで認めて下さい。

\( f'(x)=(sin x)'=\displaystyle \lim_{h \to 0} \frac{sin(x+h)-sin x}{h}\)

与式の導関数を求めます。
\( f'(x)=(sin x )'=\displaystyle \lim_{ h \to 0} \frac{sin(x+h)-sin x}{h}\)

\( = \displaystyle \lim_{ h \to 0}\ [ \frac{1}{h} (sin\ α - sin\ β)\ ]\)　

\( = \displaystyle \lim_{ h \to 0}\ [ \frac{1}{h}\ \{ 2cos (\frac{α+β}{2})\ sin (\frac{α-β}{2})\ \}\ ]\)　

\( = \displaystyle \lim_{ h \to 0}\ [ \frac{1}{h}\ \{ 2cos\ (x+ \frac{h}{2} ) \ sin　( \frac{h}{2})\ \}\ ]\)

\( = \displaystyle \lim_{ h \to 0}\ [ \ \{ cos\ (x+\frac{h}{2} )\} \ \{2\frac{1}{h} sin( \frac{h}{2})\ \} \ ]\)

\( = \displaystyle \lim_{ h \to 0}\ [ \ \{ cos\ (x+\frac{h}{2} ) \} \) \( \{ \frac{1}{\frac{h}{2}} sin( \frac{h}{2})\ \} \ ] \)

 \( \frac{h}{2}=t \)　とおくと
\( = \displaystyle \lim_{ t \to 0}\ [ \ \{ cos\ (x+t) \} \) \( \{ \frac{sin(t)}{t} \} ] \)

\( =\underline{ cos\ x \cdot 1= cos\ x } \)

導出には次の式を使います。

③ \( cosα-cosβ=- 2sin \frac{α+β}{2} sin\frac{α-β}{2} \) 【参考先】

\( f'(x)=(cos\ x )'\) \(= \displaystyle \lim_{ h \to 0} \frac{cos\ (x+h) - cos\ x}{h} \)　

\( = \displaystyle \lim_{ h \to 0}\ \frac{1}{h} [cos\ (x+h) - cos\ x ]\)

\( = \displaystyle \lim_{ h \to 0}\ -2\frac{1}{h} [sin\ (\frac{α+β}{2}) sin\ (\frac{α-β}{2}) ]\)

 以下、上記の(2)項と同様に式を展開していきます。
\( = \displaystyle \lim_{ h \to 0}\ -2\frac{1}{h} [sin\ (x+\frac{h}{2}) sin\ (\frac{h}{2}) ]\)

\( = \displaystyle \lim_{ h \to 0}\ -\frac{1}{h} [sin\ (x+\frac{h}{2}) \frac{2}{h} sin\ (\frac{h}{2}) ]\)

 \( \frac{h}{2}=t \)　とおくと
\( = \displaystyle \lim_{ t \to 0}\ -\frac{1}{h} [sin\ (x+t) \ \frac {sin\ (t)}{t} ]\)

\( =\underline{ -sin\ x \cdot 1= -sin\ x }\)

\( f'(x)=(tan\ x )'\) \(= \displaystyle \lim_{ h \to 0} \frac{tan\ (x+h) - tan\ x}{h} \)　

\(= \displaystyle \lim_{ h \to 0}\ [ \frac{1}{h} \{ tan(A - B) (1 + tan A tan B) \} ]\)

\(= \displaystyle \lim_{ h \to 0}\ [ \frac{tan(A - B)}{h} \ (1 + tan A tan B) \} ] \)

\(= \displaystyle \lim_{ h \to 0}\ [ \frac{tan(A - B)}{h} \ (1 + tan A tan B) ] \)

\(= \displaystyle \lim_{ h \to 0}\ [ \frac{tan(h)}{h} \ (1 + tan (x+h)\ tan x) ] \)

\(= 1 \cdot (1 + tan x tan x ) \) \(= (1 + tan^2x ) \)

\( = \frac{1}{cos^2x}\)

関数 f(x) が x=a で微分可能あるために、 右側微分係数 \( f'_+ (a)\) と　 左側微分係数 \( f'_- (a)\)　 が存在して、かつ 同じであることです。

右側微分係数：
\(f'_+ (a)= \displaystyle \lim_{ h \to +0} \frac{f(a+h)-f(a)}{h}\)　 \(= \displaystyle \lim_{ x \to a+0} \frac{f(x)-f(a)}{x-a}\)　

左側微分係数：
\(f'_- (a)= \displaystyle \lim_{ h \to -0} \frac{f(a+h)-f(a)}{h}\)　 \(= \displaystyle \lim_{ x \to a-0} \frac{f(x)-f(a)}{x-a}\)　

上の２式が成り立ち、２つの微分係数が同じであることが、微分可能の条件です。

\(f'_+ (a)\) \(= f'_- (a)\)

| x |の絶対値を外すと次の2通りなので x=0 で微分係数が異るので、直感的に微分不可能と想定するが、上の定義を使って微分可能性を調べます。
\( \begin{eqnarray} | x | = \begin{cases} x & ( x \geqq 0 ) \\ -x & ( x \lt 0 ) \end{cases} \end{eqnarray} \)

\(f'_+ (a)=f'_+ (0)\) \(= \displaystyle \lim_{ h \to +0} \frac{f(0+h)-f(0)}{h}\)　 \(= \displaystyle \lim_{ h \to +0} \frac{f(h)-f(0)}{h}\)　 \(= \displaystyle \lim_{ h \to +0} \frac{|h|-|0|}{h}\)　 \(= \displaystyle \lim_{ h \to +0} \frac{|1|-|0|}{h}\)　 \(= \displaystyle \lim_{ h \to +0} \frac{1}{1}\) \(=1\)　

\(f'_- (a)=f'_- (0)\) \(= \displaystyle \lim_{ h \to -0} \frac{f(0+h)-f(0)}{h}\)　 \(= \displaystyle \lim_{ h \to -0} \frac{f(h)-f(0)}{h}\)　 \(= \displaystyle \lim_{ h \to -0} \frac{|h|-|0|}{h}\)　 \(= \displaystyle \lim_{ h \to -0} \frac{|1|-|0|}{h}\)　 \(= \displaystyle \lim_{ h \to -0} \frac{-1}{1}\) \(=-1\)　

\( \therefore f'_+ (0) \ne f'_- (0) \)

この関数は x=0　において微分不可能です。

x=0 において微分係数が右側は +1 、左側は -1 です。

以下は微分の様々な定義、定理における定番な表現です。
・関数は閉区間\([a, b ]\)で連続（定義域）…\(a ≤x≤b\)
・また開区間 \((a, b )\)で微分可能ならば…\(a <x<b\)

ここでなぜ開区間 \((a, b )\)なのか
\(a <x\) 領域のある点において右側微分係数と左側微分係数が存在し、お互いに等しい意味する。
\(x<b\) 領域のある点においても同様である。

しかし端点 a では左側微分係数\( f'_- (a)\)の存在が不明である。
端点 b については右側微分係数\( f'_+ (a)\)の存在が不明である。
∴ 閉区間の両端点で微分可能が保証できないので開区間 \((a, b )\) となる。