注:\(y=\pm \sqrt{1-x^2}\)を「+」と「-」の領域の2つの関数に分けると、これを陰関数の「枝」という。
またfig2 での上下の分割は、曲線の一部の「分枝」ともいう。
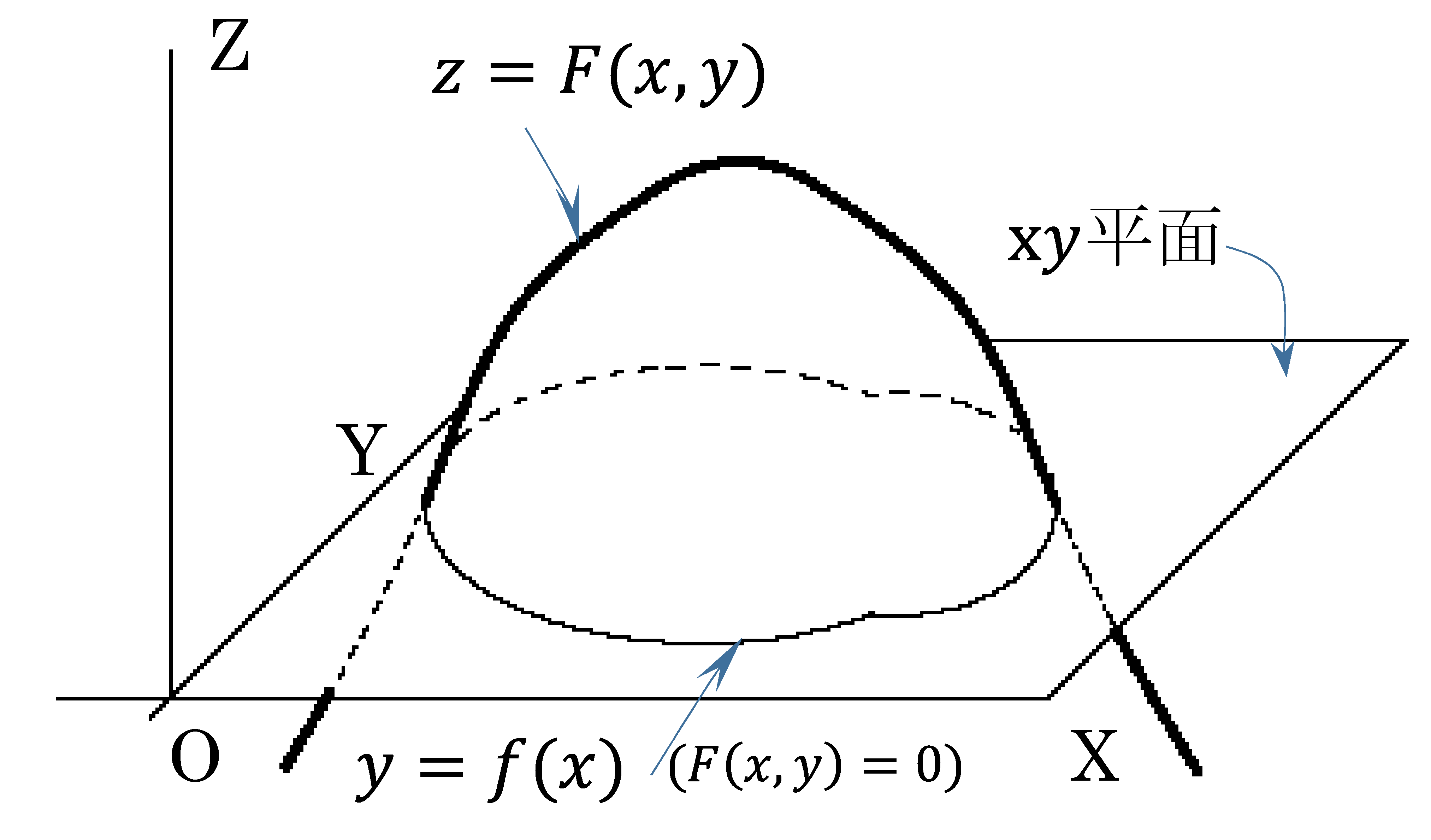
・陰関数\(y=f(x)\) は\(F(x,y)=0\) を満す、1変数関数である。
・陰関数\(y=f(x)\) は\(z=F(x,y)\)とx y平面との交わり(交線)である。(このことをfig1 で表した)
・すなわち\(F(x,y)=0\)の解の集まりが陰関数\(y=f(x)\) が描く曲線である。
区間 \(I=-1 \lt x \lt 1 \) で定義した関数 \(f(x)= \sqrt{1-x^2} \) が
\(F(x,y)=0\) を満たすとき、\(f(x)=\sqrt{1-x^2} \) を \(F(x,y)=x^2+y^2-1=0\) の陰関数という。
区間 \(I=-1 \lt x \lt 1 \) で定義した関数 \(f(x)=-\sqrt{1-x^2} \) が
\(F(x,y)=0\) を満たすとき、\(f(x)=-\sqrt{1-x^2} \) を \(F(x,y)=x^2+y^2-1=0\) の陰関数という。
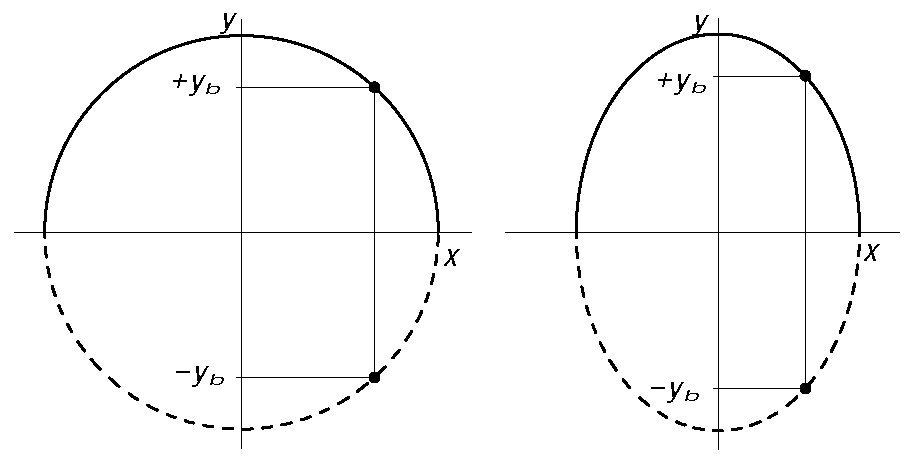
注1:(ⅲ)は陰関数\(f(x)\) が求めなくてもその導関数が求まること意味している。
注2:上記のような、陰関数\(f(x)\) が唯一存在する。
注3:例題の後で証明を行う。
\(\frac{dF}{dx}=2x +2y \cdot \frac{dy}{dx}=0\)
\(2y \frac{dy}{dx}=-2x\)
\(\frac{dy}{dx}=f'(x)=- \frac{2x}{2y}=\underline{- \frac{x}{y}}\)
\(F(x,y)=x^2+y^2-1\)として
\(F_x=\pder{F}{x}=2x\) \(\ ,\ F_y=\pder{F}{y}=2y\)
\( f'(x)=- \frac{F_x(x,f(x))}{F_y(x,f(x))}\)
\( =- \frac{2x}{2y}\)
\( =\underline{ -\frac{x}{y} }\)
\( f'(x)=- \frac{F_x(x,f(x))}{F_y(x,f(x))}\)
\( =- \frac{2x}{2y}\) \( =- \frac{x}{y}\)
(上記(1)と同じ)
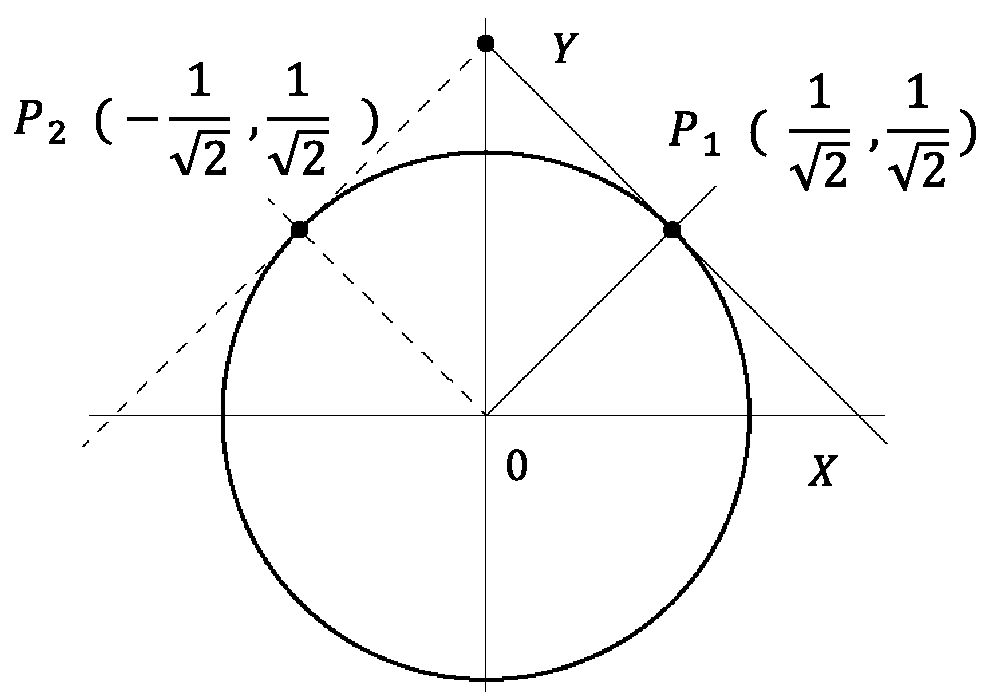
\( f'(\frac{1}{\sqrt{2}})\)\(=- \frac{2\frac{1}{\sqrt{2}}} {2\frac{1}{\sqrt{2}}}=-1\)
\(y-\frac{1}{\sqrt{2}}=-1(x-\frac{1}{\sqrt{2}})\)
\(y=-x+\frac{2}{\sqrt{2}}\)
\( f'(x)=- \frac{F_x(x,f(x))}{F_y(x,f(x))}\)
\( =- \frac{x}{y}\)
\( f'(\frac{1}{\sqrt{2}})\)\(=- \frac{2\frac{1}{\sqrt{2}}} {-2\frac{1}{\sqrt{2}}}=1\)
\(y-\frac{1}{\sqrt{2}}=1(x+\frac{1}{\sqrt{2}})\)
\(y=x+\frac{2}{\sqrt{2}}\)
\(F(x,y)=0\) を満たす陰関数\(y\) を求めることが難しいこと、求まらないこともある。
なぜなら\(y=f(x)\)は方程式\(F(x,y)=0\) の解でもあるから\(F(x,y)=0\) の内容よっては求まらないこともある。
例えば:\(F(x,y)=3xy^3+y^2+7=0\)\(,\ \) \(F(x,y)=3x\ sin(y^2)+ xy^2=0\)
など解を求るのは、難しいですね。
特異点では \(F_(x,y)=0\)で定まる陰関数の存在が不明である。
正則点の近傍では陰関数が得られ、また唯一の接線が存在する。
\(F(a,b)=0\)の導関数\(F_y\)と 陰関数\(y=f(x)\) は定義領域において連続である。
連続であればその値域は単調増加または単調減少である。これを利用して証明する。
【補足】この曲線はデカルトの正葉線(葉状曲線)という。 これを扱っている本もあるのでここでも取り上げました。
\(Fx=3x^2-3ay=0\) \(\rightarrow \) \(x^2=ay\)
\(Fy=3y^2-3ax=0\) \(\rightarrow\) \(y^2=ax\)
\(\underline{x^4}=a^2y^2=a^2(ax)=\underline{a^3x}\)
\(x^4-a^3x=\underline{x(x^3-a^3)}\)(\(=x[(x-a)(x^2+ax-a^3)])=0 \)
\(\therefore x=0\)と\(x=a\)である。
\(x=0\) に対し \(y=\sqrt{ax}=0\) ⇒候補点1=\((0,0)\)
\(x=a\) に対し \(y=\sqrt{ax}=a\) ⇒候補点2=\((a,a)\)
\(F(x,y)=0\) を満たす点は(0,0)であり、\(F_x(0,0)=F_y(0,0)=0\) である。
特異点は原点\((0,0)\)である。
点(\((a,a)\)は特異点ではない。
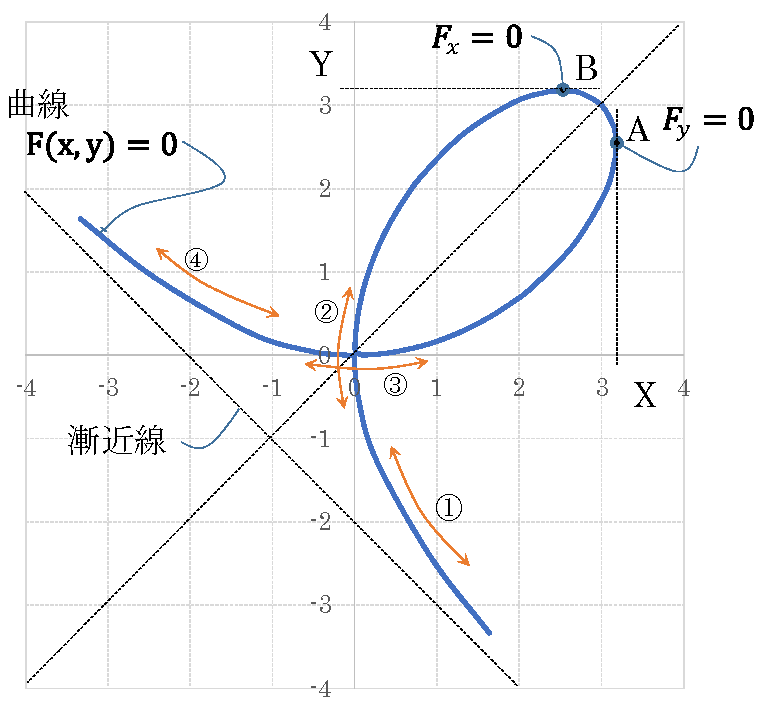
fig4 \(F(x,y)=x^3+y^3-3axy=0\)
正葉線\((a=2)\)
・直線\(y=x\)について対称。
・①↔③または④↔②の順では変化しない。
・➁と③において自分自身で交差している。
・漸近線(ぜんきんせん)※ \(y=-x-2\) が存在する。
※:x を+/ー無限にしたときに接しそうな線
漸近線\(y=-x-a\) だから\(a=2\)である(詳細省略)
\((\frac{y^2}{a})^3+y^3-3ay\frac{y^2}{a}=0\)
\((\frac{y^2}{a})^3-2y^3=0\) 次は両辺に\(a^3\)を掛ける
\(y^6-2y^3a^3=0\)
\(y^3(y^3-2a^3)=0\)
\(y=0\)は除外(対応のx が 0 であるから)
\(y^3=2a^3\) \(\ \rightarrow\) \(\underline{y=\sqrt[3]{2}a}\)
\(\underline{x}=\frac{1}{a}(\sqrt[3]{2}a)^2\) \(=\underline{\sqrt[3]{4}a}\)
\(x^3+(\frac{x^2}{a})^3 -3ax\frac{x^2}{a}=0\)
\((\frac{x^2}{a})^3-2x^3=0\) 次は両辺に\(a^3\)を掛ける
\(x^6-2x^3a^3=0\)
\(x^3(x^3-2a^3)=0\)
\(x=0\)…は除外
\(x^3=2a^3\) \(\ \rightarrow \) \(\underline{x=\sqrt[3]{2}a}\)
\(\underline{x}=\frac{1}{a}(\sqrt[3]{2}a)^2\) \(=\underline{\sqrt[3]{4}a}\)
\(F(x,y)=0\)を満たす x,y を求めてグラフ化します。
この \(F(x,y)=x^3+y^3-3axy=0\) は3次元なので、
3次式をパラメータ表示を使い、x,y を求める。
今回、x と y を求める式を作り、エクセルなどでグラフ化する前提です。
(与式を与えてグラフ化する数学ソフトは使わない)
\(t=\frac{y}{t}\)として
与式に\(y=xt\)を代入して
\(\underline{ x=\frac{3at}{1+t^3} }\)
与式に\(x=\frac{t}{y}\)を代入して
\(\underline{ y=\frac{3at^2}{1+t^3} }\)
注意点は「x が正、y が負」の領域では\(y=-\frac{3at^2}{1+t^3}\)とする。(負をつける)。
