\(f_x(a,b)\) \(= \frac{\partial f(a,b)}{\partial x}\) \(=\dot f_x(a,b)\)
\(f_y(a,b)\) \(= \frac{\partial f(a,b)}{\partial y}\) \(=\dot f_y(a,b)\)
参考に1変数関数の微分係数の定義式は:
\( f'(a)=\displaystyle \lim_{ h \to 0} \frac{f(a+h)-f(a)}{h}\)
でした。
\( f_x(a,b)=\displaystyle \lim_{ h \to 0} \frac{f(a+h,b)-f(a,b)}{h}\) \(:(a)\)
\( f_y(a,b)=\displaystyle \lim_{ k \to 0} \frac{f(a,b+h)-f(a,b)}{k}\) \(:(b)\)
\( f_x(a,b)=\displaystyle \lim_{ x \to a} \frac{f(x,b)-f(a,b)}{x-a}\) \(:(a')\)
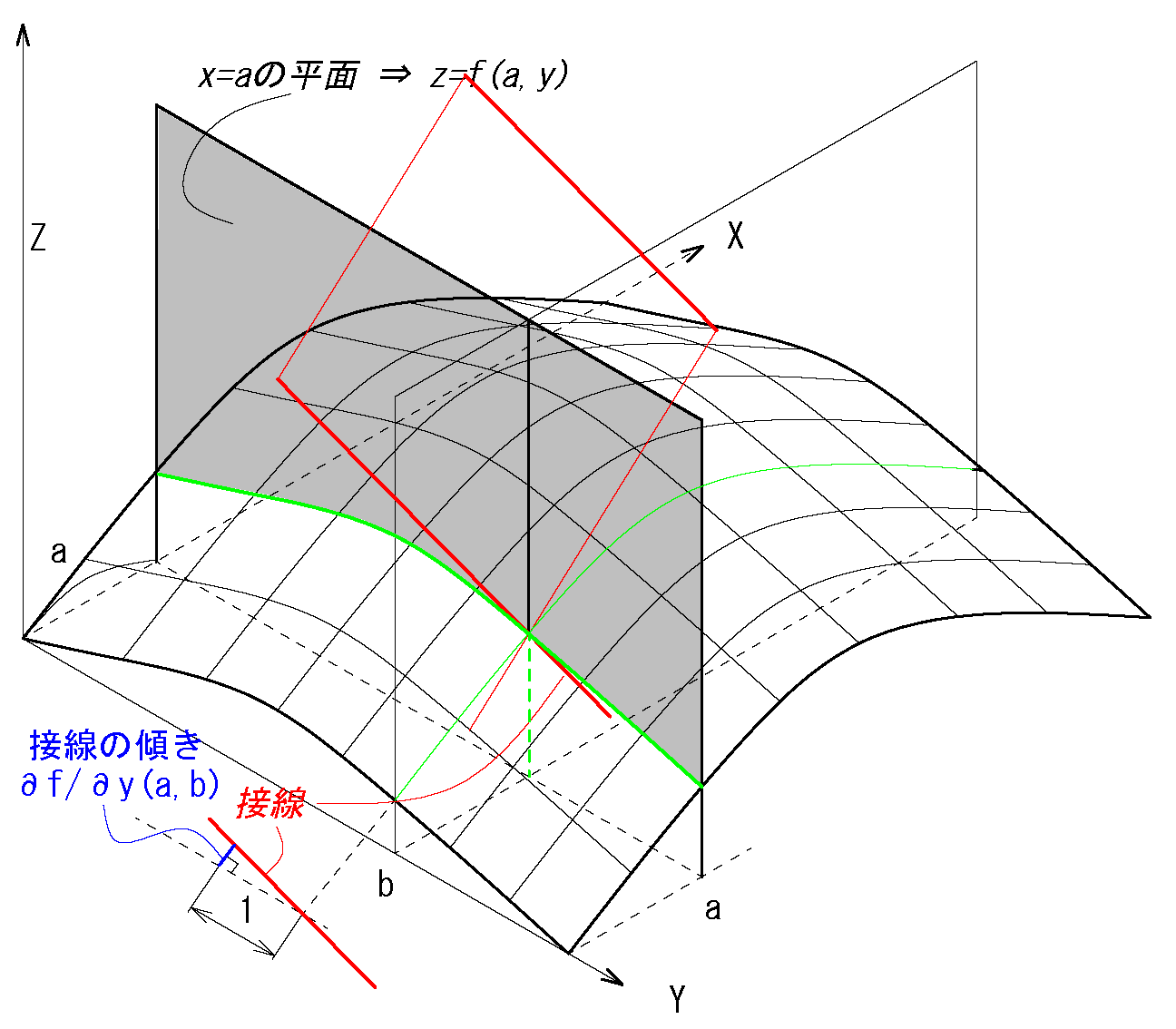
\( f_y(a,b)=\displaystyle \lim_{ y \to b} \frac{f(a,y)-f(a,b)}{y-b}\) \(:(b')\)
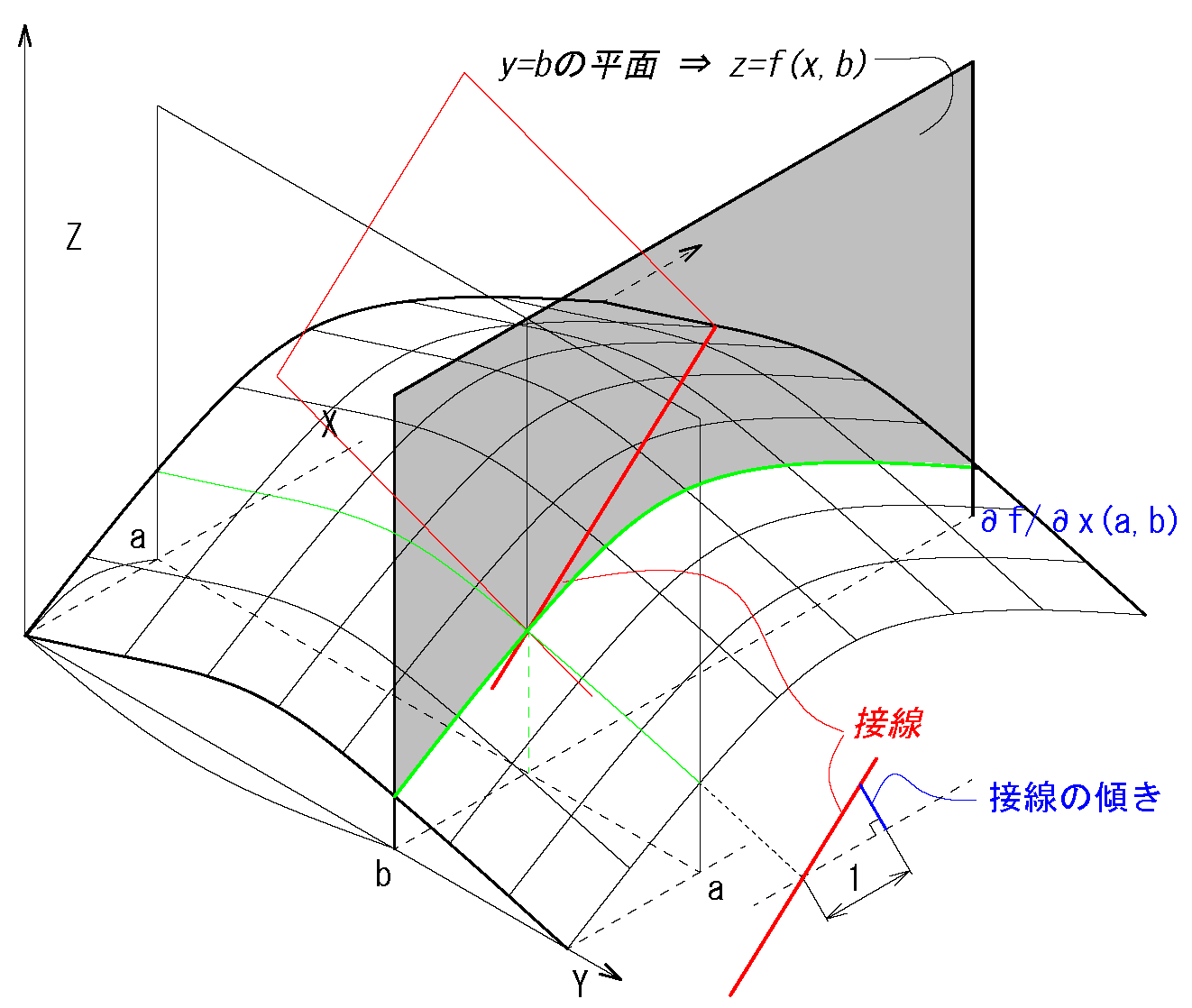
\(f_x=z_x= \left( \frac{\partial f}{\partial x} \right)_y\) \(= \frac{\partial f}{\partial x} =\dot f_x\)
\(f_y=z_y= \left( \frac{\partial f}{\partial y} \right)_x\) \(= \frac{\partial f}{\partial y} =\dot f_y
\)
\( f_x(x,y)=\displaystyle \lim_{ h \to 0} \frac{f(x+h,y)-f(x,y)}{h}\)
:\((a1)\)
(xが変数、yは定数)
\( f_y(x,y)=\displaystyle \lim_{ k \to 0} \frac{f(x,y+k)-f(x,y)}{k}\)
:\((b1)\)
(yが変数、xは定数)
偏微分定義の式(a),(b)を使う。(式の定義より\(f(0,0)=0\))
\( f_x(0,0)=\displaystyle \lim_{ h \to 0} \frac{f(a+h,b)-f(a,b)}{h}\)
\(=\displaystyle \lim_{ h \to 0} \frac{f(h,0)-f(0,0)}{h}\)
\(=\displaystyle \lim_{ h \to 0} \frac{0-0}{h}\)
\(=\displaystyle \lim_{ h \to 0} \frac{0}{h}\) \(=0\)
(極限を取る前に式は「0 」になる。0/0 の不定形にはならない)
従って(x,y)=(0,0) において\(f_x(0,0)\)が存在し、偏微分可能である。しかし関数は連続ではない(*)。
(* )\( \because (x,y)=(0,0)\) での極限がなく、\(f(0,0)\)も存在しないから。
また同様にして \(f_y(0,0)\)についても同様の結果を得る。
\(f(x)=f(a)+m(x-a)+r(x)\) \(,\ \underline{\lim_{x \to a} |\frac{r(x)}{x-a}|=0}\) \(\quad (c)\)
\(r(x)\)を誤差項と呼び、
\(x\rightarrow 0 \) において下線部(誤差項)は「0」となる。
微分可能なら 誤差項部は「0」、上記の m は接線の傾きで微分係数である。式(c)は接線の方程式となる、つまり
\(f(x)=f'(a)(x-a)+f(a)\) である。
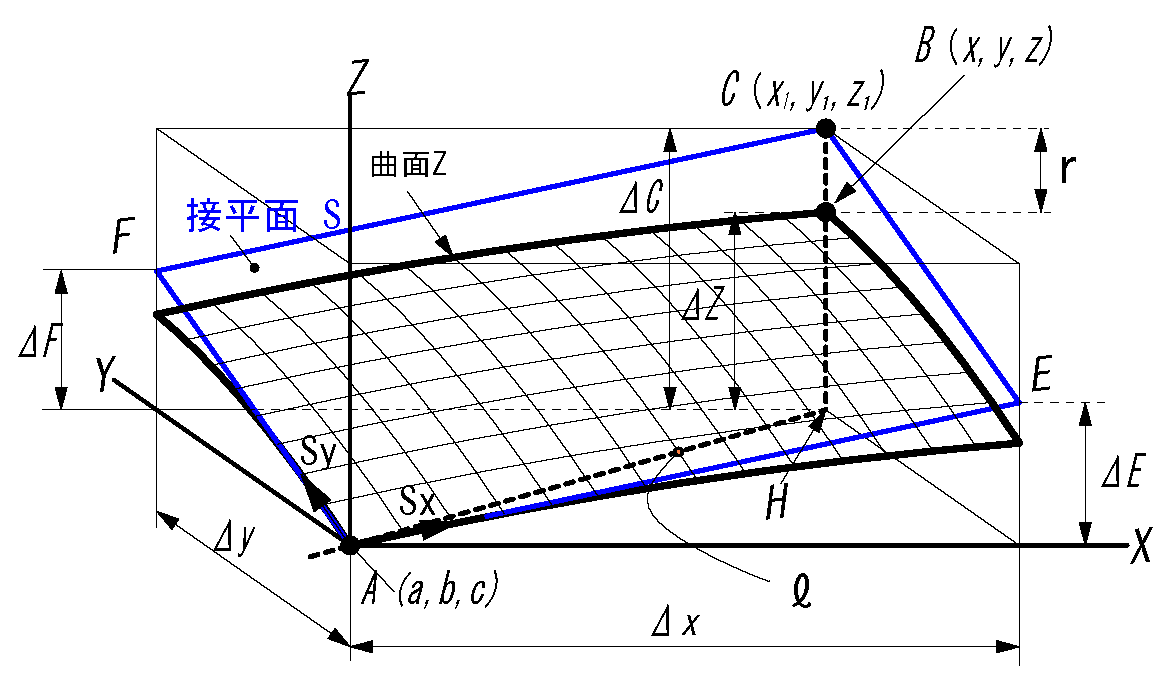
\(f(x,y)-f(a,b) \)
\(=\frac{\partial f(a,b)}{\partial x}(x-a)\) \(+\frac{\partial f(a,b)}{\partial y}(y-b)\) \( \quad (d) \)
\(f(x,y)-f(a,b) \) \( =m_x (x-a) + m_y(y-b) \) \( \quad (d') \)
単位ベクトルの成分: \( s_x=(1,0,m_x), s_y=(0,1,m_y) )\)より
接線の傾きは:
\(m_x=f_x(a,b)=\frac{\partial f(a,b)}{\partial x}\) \(,\)
\(m_y=f_y(a,b)=\frac{\partial f(a,b)}{\partial y}\)
\(\frac{x-a}{f_x(a,b)}=\frac{y-b}{f_y(a,b)}=\frac{z-f(a,b)}{-1}\) \( \quad (e) \)
\( \bv{n}=S_x \x S_y= \begin{pmatrix} 1\\ 0\\ f_x \end{pmatrix} \) \(\x \begin{pmatrix} 0\\ 1\\ f_y \end{pmatrix} \) \(= \begin{pmatrix} -f_x\\ -f_y\\ 1 \end{pmatrix} \)
原点 O(0,0,0)として、\(\bv{n}\)の始点A(a,b,f(a,b))、\(\bv{n}\)の延長上(t倍)の任意の点 P(x,y,z)とする。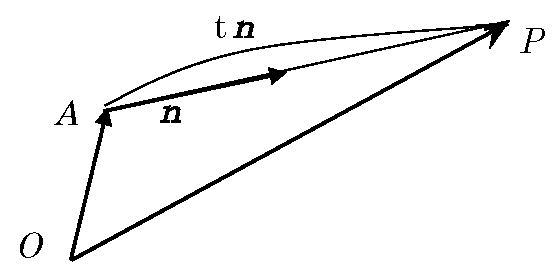
\(\vec{OP}=\vec{OA}+t\ \bv{n}\) をもとに:
\(\vec{OP}=(x,y,z)\)\(\quad\) \(\vec{OA}=(a,b,f(a,b))\)
\(\quad\) \( \bv{n}=(-f_x,-f_y,1)\)
\(
\begin{pmatrix}
x\\
y\\
z
\end{pmatrix}
\)
\(=
\begin{pmatrix}
a\\
b\\
f(a,b)
\end{pmatrix}
\)
\(+ t\
\begin{pmatrix}
-f_x\\
-f_y\\
1
\end{pmatrix}
\)
ベクトルA とB の外積「\(A \times B=C\)」とは⇒A とB が張る平面に垂直なベクトル C である。
【参考先】
ベクトルA とB の内積「\(A \cdot B=0\)」のとき、A とB は平行である。
【参考先】
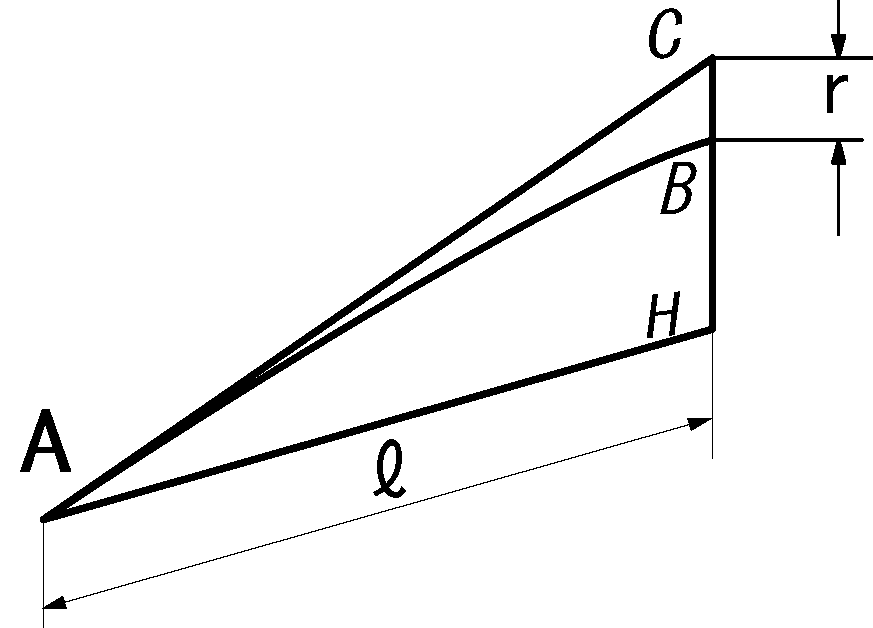
\(x-a=\Delta x=h, \ x-b=\Delta y=k\)\(,\) \(ℓ=\sqrt{h^2+k^2}\)として
\(f(x,y)=f(a,b)+m_x(x-a)\)\(+m_y(y-b)\)\(+\color{red}{o(ℓ(h,k))}\) \(\ :(f)\)
\(f(x,y)=f(a,b)+m_xh+m_yk\) \(+\color{red}{o(ℓ(h,k))}\) \(\ :(f')\)
式(f)が成り立つとは、誤差項は「0」、そして
\(m_x=f_x(a,b), \ m_y=f_y(a,b)\)→これは接線の傾きです。
すなわち下式が成り立つ:
\(f(x,y) = f(a,b)+ f_x(a,b) (x-a)\)\(+ f_y(a,b) (y-b)\)
\(f(x,y)-f(a,b) = m_x (x-a)\)\(+ m_y(y-b)+r(h,k)\) \(\quad (f'')\)
\(r(h,k)\)\(=f(x,y)-f(a,b)\)\(-m_x(x-a)-m_y(y-b)\)
\(o(ℓ(h,k))\)の「\(o(\dots)\)」をランダウ記号という。
rは曲面を接平面で近似したときの誤差です。
\(o(ℓ(h,k))=\displaystyle \lim_{(h,k) \to (a,b)} \frac{r(h,k)}{ℓ(h,k)}=0\) ❶
式❶は「0」に収束する速度が分子のr(h,k)ほうが分母より早いことを意味する。
(分子が早く「0」になるので、この極限「0」に収束する。)
これを\(r(h,k)\)は\(ℓ(h,k)\)より高位の無限小という。
また、
\(\color{fuchsia}{ r(h,k)=o(ℓ(h,k))}\) ❷
と書くと式❶を意味する。
(※1)を参考に式(f)を変形すると:
・\(\displaystyle\lim_{(h,k) \to (a,b)} \frac{\color{red}{r(h,k)}}{ℓ(h,k)}\)
\(=\displaystyle\lim_{(x,y) \to (a,b)} \frac{\color{red}{r(h,k)}}{\sqrt{h^2+k^2}}=0\)
\(\ :(g)\)
\(\sqrt{h^2+k^2}=\sqrt{(x-a)^2+(y-b)^2}\)
(h,k)→(a,b) のとき (x,y)→(a,b) である。
・\( \color{red}{r(h,k)}\)\(=f(x,y)-f(a,b)\)\(-f_x(a,b)h-f_y(a,b)k\)\(=0\)\(\ :(h)\)
となる。
\(df=\)\(f_x(x,y)dx +f_y(x,y)dy\) \(\quad (i)\)
\(f_x= \dd{}{x}(-2x^2-y^2)\) \(=2\cdot (-2)x=-4x\)
\(f_y= \dd{}{x}(-2x^2-y^2)\) \(=2\cdot (-1)2=-2y\)
\(f_x(1,1)=-4 \cdot 1=-4\) \(\quad\)
\(f_y(1,1)=-2 \cdot 1=-2\)
\(f(a,b)=f(1,1)=-3\)
\(f(x,y)=f_x(a,b)(x-a)\)\(+f_y(a,b)(y-b)+f(a,b)\) \(=-4(x-1)-2(y-1)-3\) \(=-4x-2y+3\)
法線は式(e)より
\(\frac{x-a}{f_x(a,b)}=\frac{y-b}{f_y(a,b)}\) \(=\frac{z-f(a,b)}{-1}\)
\(\frac{x-1}{-4}=\frac{y-1}{-2}\)\(=\frac{z+3}{-1}\)
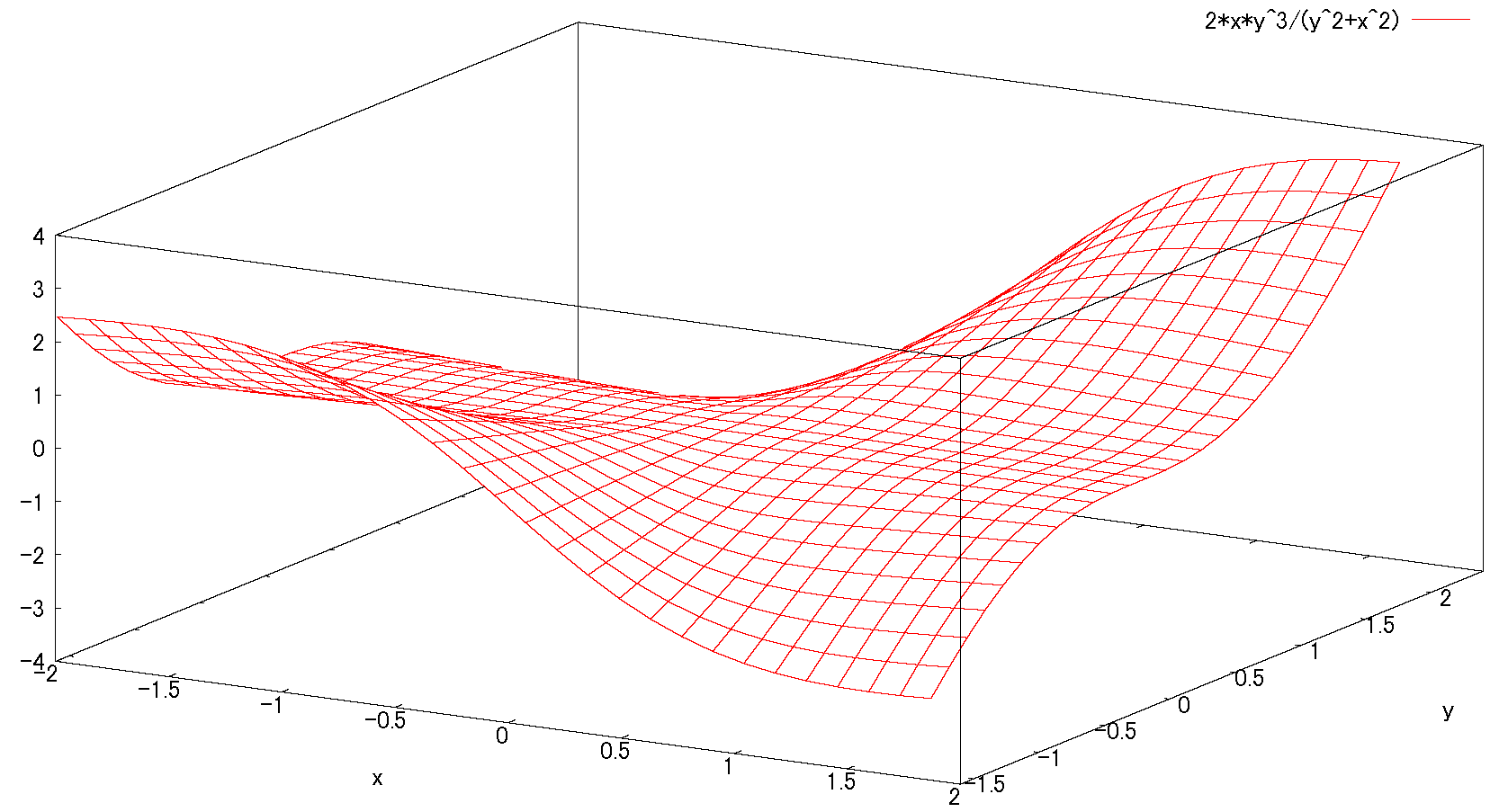
\( \begin{eqnarray} z= \begin{cases} \frac{2xy^3}{x^2+y^2} & (x,y)\ne (0,0) \\ 0 & (x,y)=(0,0) \end{cases} \end{eqnarray} \)
\(\underline{f(0,0)=0}\) (与式より)
\( f_x(a,b)=\displaystyle \lim_{ h \to 0} \frac{f(a+h,b)-f(a,b)}{h}\)\(\quad (a)\)
\(\underline{f_x(0,0)}=\displaystyle \lim_{ h \to 0} \frac{f(h,0)-f(0,0)}{h}\)
\( =\displaystyle \lim_{ h \to 0} \frac{0}{h}\ \underline{=0}\)
\( f_y(a,b)=\displaystyle \lim_{ h \to 0} \frac{f(a,b+h)-f(a,b)}{h}\) \(\quad (b)\)
\(\underline{f_y(0,0)}=\displaystyle \lim_{ h \to 0} \frac{f(0,h)-f(0,0)}{h}\)
\( =\displaystyle \lim_{ h \to 0} \frac{0}{h}\ \underline{=0}\)
\(\displaystyle \lim_{(h,k) \to (0.0)} \frac{r(h,k)}{h^2+k^2}\)\( \quad (g) \)
\( =\displaystyle \lim_{(h,k) \to (0.0)} \frac{2hk^3}{h^2+k^2} \frac{1}{\sqrt{h^2+k^2}}\)
\( =\displaystyle \lim_{(h,k) \to (0.0)} \frac{2hk^3}{(h^2+k^2)^{\frac{3}{2}} }\)
分母に\((h^2+k^2)\)の項があるので極座標変換すると簡単になりそうである。
\(h=r cosθ,\ k=r sinθ\)、また \(r \rightarrow 0\)の極限として上式を変形する。
\( =\displaystyle \lim_{r \to 0} \frac{2rcosθ (r sinθ)^3}{(r^2 cos^2θ+r^2 sin^2θ)^{\frac{3}{2}} }\) \( =\displaystyle \lim_{r \to 0} \frac{2 r^4 cosθ (sinθ)^3}{r^{ 2{\frac{3}{2}} }(cos^2θ+sin^2θ)^{\frac{3}{2}} }\) \( =\displaystyle \lim_{r \to 0} \frac{2 r^4 cosθ (sinθ)^3} { r^3 \cdot 1 }\) \( =\displaystyle \lim_{r \to 0} \ 2 r cosθ (sinθ)^3\) \(=0\)
従って与式は全微分可能である。
