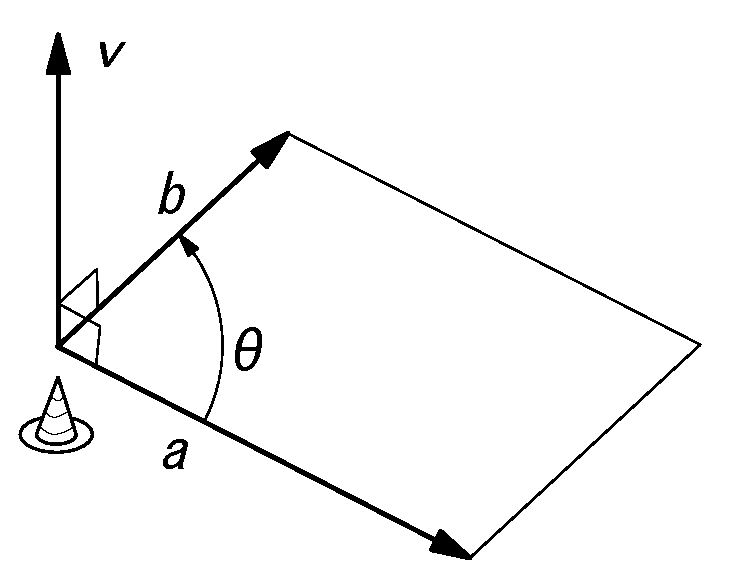
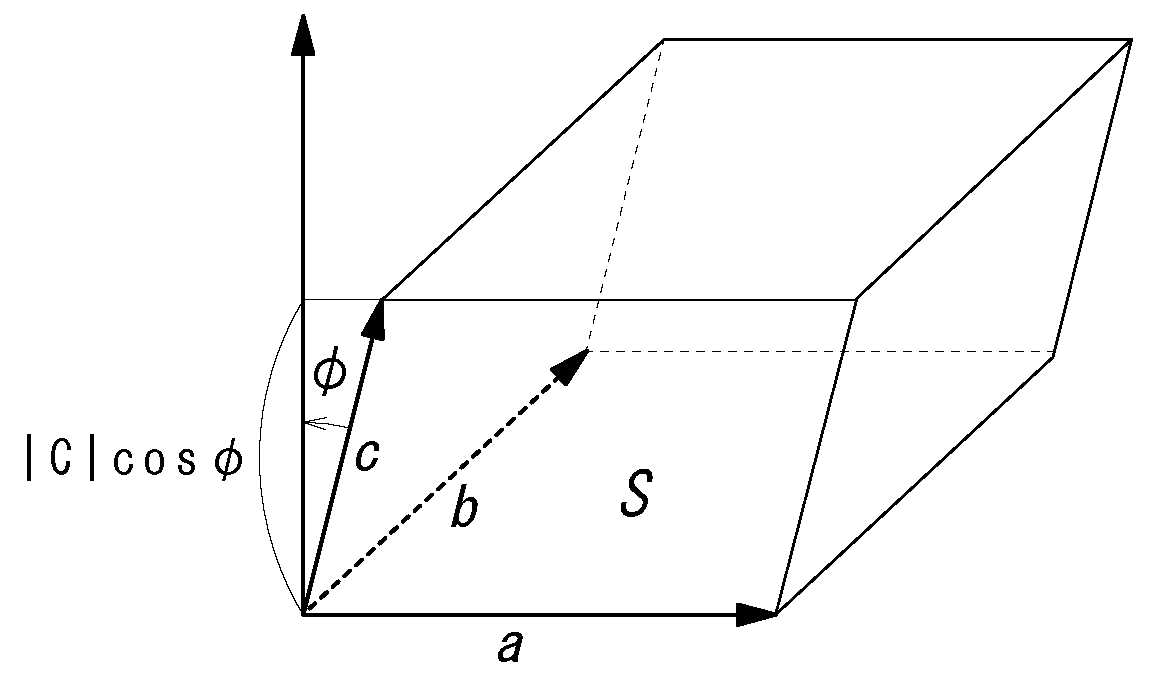
左辺を2乗すると:
\( (|a||b|sin θ)^2=|a|^2 |b|^2 sin^2 θ\)
\(=|a|^2|b|^2(1-cos^2 θ)\)
\(=|a|^2 |b|^2-\underline{|a|^2 |b|^2 cos^2 θ } \)
\(=|a|^2 |b|^2-\underline{(a\cdot b)^2} \) (※1)
注(※1):内積の性質から
\( (a\cdot b)=|a||b| cos\ θ \)
である。
上式が「ベクトルa とb の外積」になるかを証明すればよい。
\(a=(a_1,a_2,a_3), \ b=( b_1,b_2,b_3)\) として右辺を展開すると:
\(S^2=\underline{|a|^2 |b|^2} -(a \cdot b)^2 \)
\(=\underline{(a_1^2+a_2^2 +a_3^2) (b_1^2+b_2^2+b_3^2)} \)
\( -(a_1 b_1+a_2 b_2+a_3 b_3)^2\)
上式の展開に疑問の方は
【ここを参照】
\(=a_1^2 b_1^2+a_1^2 b_2^2+a_1^2 b_3^2\)\(+a_2^2 b_1^2 +a_2^2 b_2^2 +a_2^2 b_3^2\)
\(+a_3^2 b_1^2 +a_3^2 b_2^2 +a_3^2 b_3^2\)
\(- 2 a_1 a_2 b_1 b_2\) \(- 2 a_1 a_3 b_1 b_3\) \(- 2 a_2 a_3 b_2 b_3\)
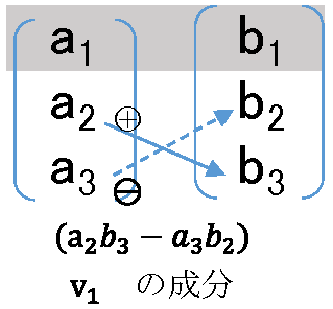
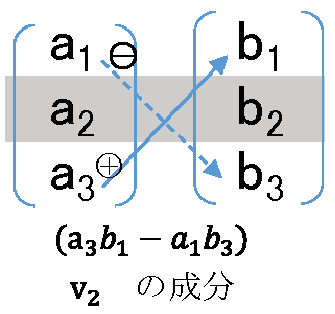
\(=(a_2 b_3-a_3 b_2)^2 + (a_3 b_1-a_1 b_3)^2 \)
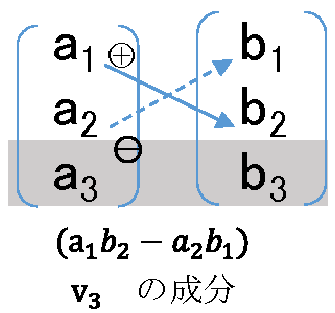
\( + (a_1 b_2-a_2 b_1 )^2\)
上式は以下のベクトル積ですね
【ここを参照】
\(=
\left(
\begin{array}{c}
a_2 & b_2 \\
a_3 & b_3
\end{array}
\right)^2
\)
+
\(\left(
\begin{array}{c}
a_3 & b_3 \\
a_1 & b_1
\end{array}
\right)^2
\)
\( \quad
+
\left(
\begin{array}{c}
a_1 & b_1 \\
a_2 & b_2
\end{array}
\right)^2
\)
\(=(a \times b)^2\)
\( \therefore \ S=\sqrt{(a \times b)^2}=a \times b \ \) 証明終わり