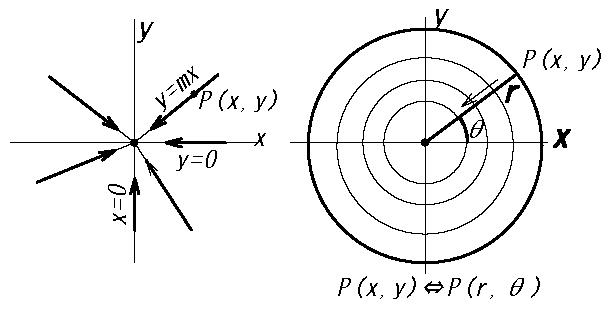楽しく学ぶ…微分積分
多変数関数の連続性
(continuity of multivariable function)
--目 次--
多変数関数とグラフ
本文に入る前に以下に注意!
\(\bv{R}^2\) は2次元、\(\bv{R}^3\) は3次元のユークリッド空間のことで高校数学で考えた普通の空間のこと。詳しくは【参照先】
\(\bv{R}^n\) の\(\bv{R}\) は実数、\( n\) は次元を示す。
ここでは、多変数の微分(偏微分)に進むまえの準備として、3次元空間における
2変数の関数の極限と連続性について学びます。
2変数の微分は1変数と比べ、配慮すべきことが増えます、また3変数以上の関数は2変数の拡張と考えます。
一般的に多変数といっても扱くのは2変数が多く、グラフにより可視化できるのは2変数の3次元空間までです。
数学では何次元でも書けるが、一般にグラフで図示できる3次元までである。
また特殊相対論などでは時間 \(t\) を含め4 次元を扱っている。
2次元空間\(\bv{R}^2\) の定義域の\(D\)は1変数 \(x\) が動く範囲のこと、また
関数 f は定義域の変数に対しただ1つ定まる実数である。
(変数x はx 軸座標上(数直線 )を動く
数列である)
3次元空間\(\bv{R}^3\) の定義域の\(D\)は 2変数が \(x y\)平面上を動く範囲のこと、また
関数 f は定義域の変数に対しただ1つ定まる実数である。
(変数x, y はxy平面を動く点(x,y)からなる、
点集合である)
4次元以上も同様な考え方だが変数は \((x,y,z \cdots)\) ではなく
\((x_1,x_2,x_3,x_4,\cdots\)) と書くのが一般的である。
(分かりにくいが、使っている本もあるので簡単に説明を付記しておく)
関数\(f\)の定義:
定義域 D は実数\((D\subset \bm{R})\) として
・\(\underline{ f:D \rightarrow \bv{R} }\)
関数 f の 変数の定義域 D から 実数 \(\bv{R}\) への写像(関数は写像である)
【参照先】
関数\(f\)の値域とは:
(定義域\(D\)における関数のとりうる値):
(集合記号で表わす【参照先】)
\(\bv{R}^2\)のとき:\(f(D)=\{f(x)\) \(\ | x \in D \}\)
\(\bv{R}^3\)のとき:\(f(D)=\{f(x,y)\) \(\ | (x,y) \in D\} \)
\(\bv{R}^{n+1}\)のとき: \(f(D)=\{f(x_1,x_2,\cdots x_n)\) \(\| (x_1,x_2,\cdots x_n) \in D\} \)
関数\(f\)のグラフとは:
\(\bv{R}^3\)のとき
定義域 \(D\)(平面)の\((x,y)\) に対応する点\((x,y,f(x,y))\) の集合である。
上記を集合の式で表すと:
\(\bv{R}^2\)のとき: \(\{(x,f(x))\in R^2 \)\(\ | x \in D\} \)
\(\bv{R}^3\)のとき:\(\{ (x,y,f(x,y))\in R^3 \)\(\ |(x,y) \in D \} \)
\(\bv{R}^{n+1}\)のとき: \(\{(x_1,\cdots x_n,f(x_1,\cdots x_n) \in R^{n+1}\) \(\| (x_1,\cdots x_n) \in D \} \)
グラフは次元により、\(\bv{R}^2\)では
曲線、\(\bv{R}^3\)では
曲面である。
一般に2変数の式から3次元グラフの形状をイメージするのは難しい。
3次元ソフトを使わず3次元グラフの形状を可視化する方法は等高線などの切り口の曲線を使うのが一般的である。(後で例題で扱う)
多変数関数の極限
2変数の場合、下図のように xy平面上の点 A(a,b) へ近づける方法(直線、曲線、回転)は様々ある。
xy平面上の点 \(A(a,b)\),それに対応する曲面の Z 上の点を \( B(a,b,f(a,b))\)とする。
このとき \( \displaystyle \lim_{(x,y) \to (a,b)} f(x,y)=α\) と仮定すると
この仮定は点B における Z の値が α であり、α は極限値を示す。(\(z=f(a,b) \rightarrow α\))
( D は 定義域(x-y平面)、\(z=f(x,y)\) は値域)
2変数のときの極限は点 A (a,b)への近づき方によらず 定点 \(z=α\) となることである。
また、点A へに近くづくとは「点A との距離が短くなる」ことである。
1変数の場合、変数が x軸(数直線)上を 点 a に 左の(-)から、右の(+)から 2通り で近づき、a に対応するf(a) の極限を調たが、
2変数の場合、定義域内の xy平面上の点 が 様々な方向から点 A(a,b) に近づくので、その近づき具合を点 A(a,b)と点d(x,y)の距離で表わす。
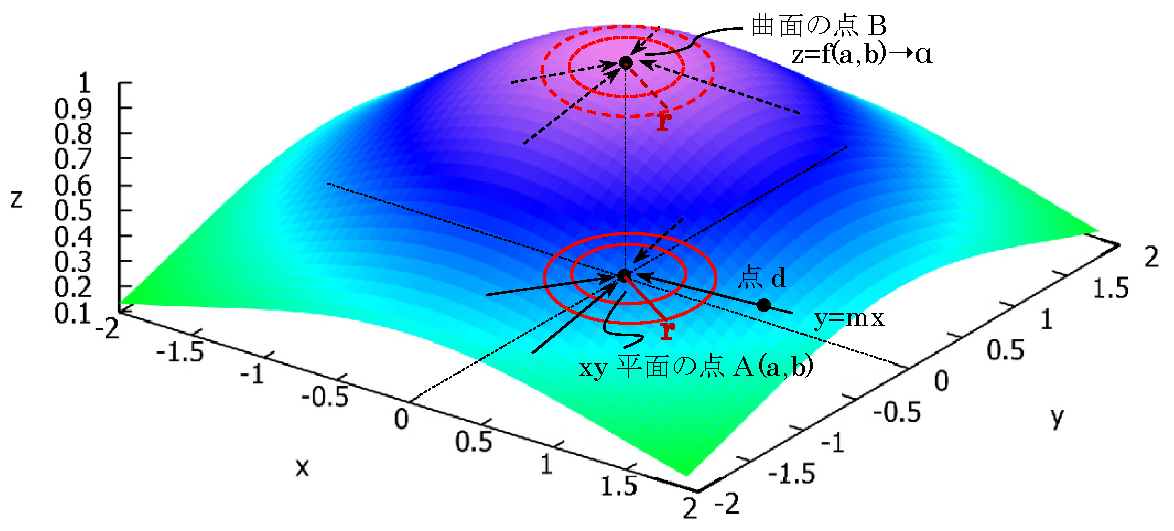
fig1 \(z=e^{-(x+y)}\)
fig1の補足:
・ある点\((x,y)\)と点\(A(a,b)\)の2点間の距離は \(ℓ=\sqrt{(x-a)^2 + (y-b)^2}\)である。
・\(xy\)平面上を動点d が 距離ℓ を縮めて 定点\(A(a,b)\) に近づていくイメージ。
今までの説明をもとに\(ε-\delta\)論法で「2変数関数の極限」を定義する。
(慣れていないと 分かりにくいですね!)
2変数関数の極限
(\(ε-\delta\) 論法)【参照先】
\(f\) は \(x-y\)平面の\(D\)上で定義された2変数関数、\((a,b)\)は\(D\)上の点とする。
\((f:D \rightarrow \bv{R})\)
以下は\((x,y)\) の点 \((a,b)\)への近づき方によらず成り立つこと。
任意の \(ε\gt 0 \) に対して、
\((x,y) \in D\) かつ \(0 \lt \sqrt{(x-a)^2 + (y-b)^2}(=ℓ) \lt \delta\) ならば
\(|f(x,y)-α| \lt ε \) となる \(\delta \gt 0\) が存在するとき、
\(f(x,y)\) は \(α\) に収束し、
\( \displaystyle \lim_{(x,y) \to (a,b)} f(x,y)=α\) である。
\(((x,y)\rightarrow(a,b)\) のとき \(f(x,y)\rightarrow α)\)
|
上記を論理記号で書く(多変数関数の極限)
•\(\ \forall ε \):「すべてのε (all)」または「任意のε (any)」
•\(\ \exists δ \):「δが存在する (exist)」
•\(\ s.t.A \):「Aのような (such that)」
•\(\ A \Rightarrow B \):「AならBである」
•以下の括弧()は見やすくするだけのもの。
|
\(ε,\delta \in \bv{R}\) \(\quad \bv{ℓ}=\sqrt{(x-a)^2 + (y-b)^2}\)として
以下は\((x,y)\) の点 \((a,b)\)への近づき方によらず成り立つこと。
\( \forall ε\gt 0 \quad \exists δ \quad s.t.\)
\( (\forall(x,y)\in D)\) \(,\) \( (0 \lt \bv{ℓ} \lt \delta) \)
\(\Rightarrow |f(x,y)-α|\lt ε\)
どんなに小さな正の実数ε に対し、ある正の実数δ が存在し、
f(x,y) の定義域D 内の かつ \(0\lt \bv{ℓ} \lt \delta\) ならば
\(|f(x,y)-α|\lt ε\)である。
|
2変数関数の極限の調べる方法
(x,y)平面上において、その原点(0,0) に近づく具体的な方法はある直線で近づく方法と回転しながら近づく方法がある。
・直線では、\(y=mx\) とか x軸(\(y=0\))、 y軸(\(x=0\)) などに沿って近づける。
・回転では、極座標に変換して動径\(r\) を小さくして近づける。
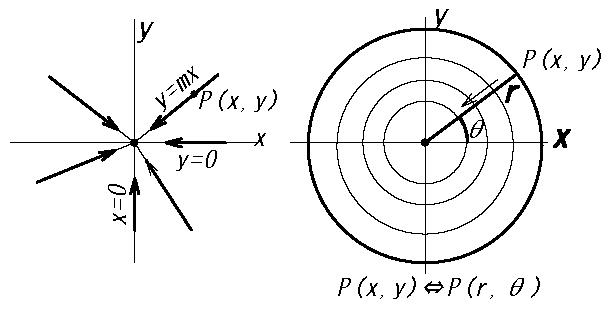
fig2 極限に近づく方法
では2つの代表的な2変数関数の極限を調べみよう。
例題1:
次の関数の原点(0,0)での極限値を求めよ
\(
\begin{eqnarray}
f(x,y)=
\begin{cases}
\frac{2xy}{x^2+y^2} & (x,y)\ne (0,0) \\
0 & (x,y)=(0,0)
\end{cases}
\end{eqnarray}
\)
次の2通りで解答する。
ⓐ直線に沿って近づける(直線:
\(y=mx\))
与式にy にmx を代入
\(f(x,mx)=\frac{2xmx}{x^2+(mx)^2}\)\(=\frac{2mx^2}{x^2(1+m^2)}\)\(=\frac{2m}{1+m^2}\)
\(\displaystyle \lim_{(x,y) \to (0,0)} f(x,mx)\)\(=\frac{2m}{1+m^2}\)
極限は \(m\) に依存し、\(m=1\)のときは\(\frac{2}{2}=1\)、 \(m=0\)(※1)のとき\(0\)となる。
このことは原点(0,0) への
近づき方により 極限値が異なる。
\(\therefore\)
極限はない。
注1(※1):\(m=0\) のときは\(y=0\) だから \(x\)軸に沿って近づくことを意味する。
注2:極限がない結果がでれば、ここで終了する。次のⓑは参考です。
ⓑ原点のまわりを回転して近づける。
すなわち
極座標に変換し、原点に近づける極限を調べる。
\((x,y)=\color{red}{(rcosθ,r sinθ)}\)
\(f(x,y)= \frac{2xy}{x^2+y^2}\) \(=2\frac{(rcosθ) (rsinθ)}{(rcosθ)^2+(rcosθ)^2}\)
\(=\frac{r^2(cosθ) (sinθ)}{r^2((cosθ)^2+(sinθ)^2)}\)\(=2cosθ\ sinθ \)
\(\therefore \)
\(\displaystyle \lim_{r \to 0} f(rcosθ,r sinθ)\) \(=\displaystyle \lim_{r \to 0} 2 cosθ\ sinθ\)
このことは原点(0,0) への
近づき方の角\(θ\) により 極限値が異なる。
\(\therefore\)
極限はない。 (fig3 参照➝
原点周辺に穴が開いている)
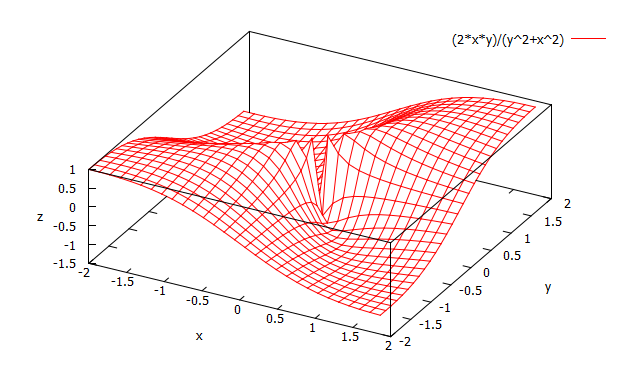
fig3 \(\frac{2xy}{x^2+y^2}\)
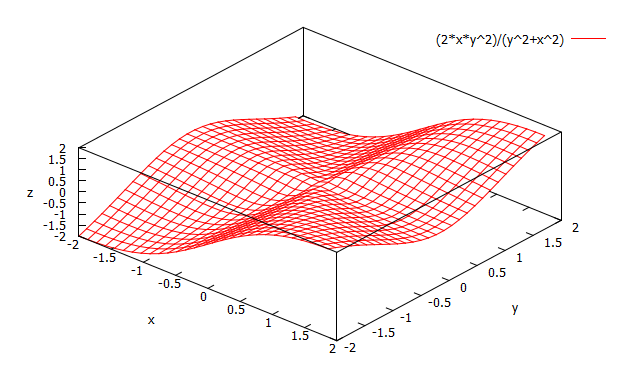
fig4 \(\frac{2xy^2}{x^2+y^2}\)
次の関数の原点(0,0)での極限値を求めよ
\(
\begin{eqnarray}
f(x,y)=
\begin{cases}
\frac{2xy^2}{x^2+y^2} & (x,y)\ne (0,0) \\
0 & (x,y)=(0,0)
\end{cases}
\end{eqnarray}
\)
例題1の式とよく似ているが?
ⓐ直線に沿って近づける(
\(y=mx\))
\(f(x,mx)=\frac{2x(mx)^2}{x^2+(mx)^2}\)\(=\frac{2m^2x^3}{x^2(1+m^2)}\)\(=\frac{2m^2}{1+m^2}x\)
\(\displaystyle \lim_{(x,y) \to (0,0)} f(x,mx)\)
\(=\displaystyle \lim_{\color{blue}{(x,y) \to (0,0)}}\frac{2m^2}{1+m^2}\color{blue}{x}=0\)
極限は \(m\) に依存せず、
\(0\) に収束する。
\(\therefore\)
極限は存在する。(=0)
ⓑ原点のまわりを回転して近づける。
この
すなわち
極座標に変換し、\(r\)原点に近づけて極限を調べる。
\((x,y)=\color{red}{(rcosθ,r sinθ)}\)
\(f(x,y)= \frac{2xy}{x^2+y^2}\) \(=\frac{2(rcosθ) (rsinθ)^2}{(rcosθ)^2+(rcosθ)^2}\)
\(=\frac{2r^3(cosθ) (sinθ)^2}{r^2((cosθ)^2+(sinθ)^2)}\)\(=2\ r cosθ\ (sinθ)^2 \)
\(\therefore \)
\(\displaystyle \lim_{r \to 0} f(rcosθ,r sinθ)\)
\(=\displaystyle \lim_{\color{blue}{r \to 0}} 2\ \color{blue}{r} cosθ\ (sinθ)^2=\color{blue}{0} \)
極限は \(θ\) に依存せず、
\(0\) に収束する。
極座標による方法の結果
「\(θ→\infty\)」と「\(r→0\)」により近づくから、原点にはあらゆる近づき方をしたことになる。
・「\(θ\)」に依存せず,定義域内の「\(r\)」に関して「極限の存在」が確認できたことになる。
・原点への近づき方に依らず成り立ったことになる。
\(\therefore\)
極限(=0)は存在する。 (fig5 参照)
3Dソフトを使わず 曲面をイメージするには曲
面の切り口の
曲線を調べるのが一般的です。
・ Z=定数のxy平面に平行な面での切り口の曲線、すなわち
等高線(fig6)
・ 等高線以外の曲線。例えば y軸に垂直な面での
切り口の曲線(fig7)
曲面の等高線
\(z=\sqrt{\frac{x^2}{4}+\frac{y^2}{1}}\)
の等高線を求める
\(z=1\)のとき、両辺を2乗すると
\(1=\frac{x^2}{2^2}+\frac{y^2}{1^2} \)
これは楕円の方程式である。
\(1=\frac{x^2}{a^2}+\frac{y^2}{b^2} \) \((a\lt b\lt 0) \)
・長軸の長さ\(=2a=2\cdot2=4\) ・短軸の長さ\(=2b=2\cdot1=2\)
(a=b のときは円である)
\(z=2\)のときは(式変形して)
\(1=\frac{x^2}{4^2}+\frac{y^2}{2^2} \)
・長軸の長さ\(=2a=2\cdot4=8\) ・短軸の長さ\(=2b=2\cdot2=4\)
⇒fig6 等高図 を参照
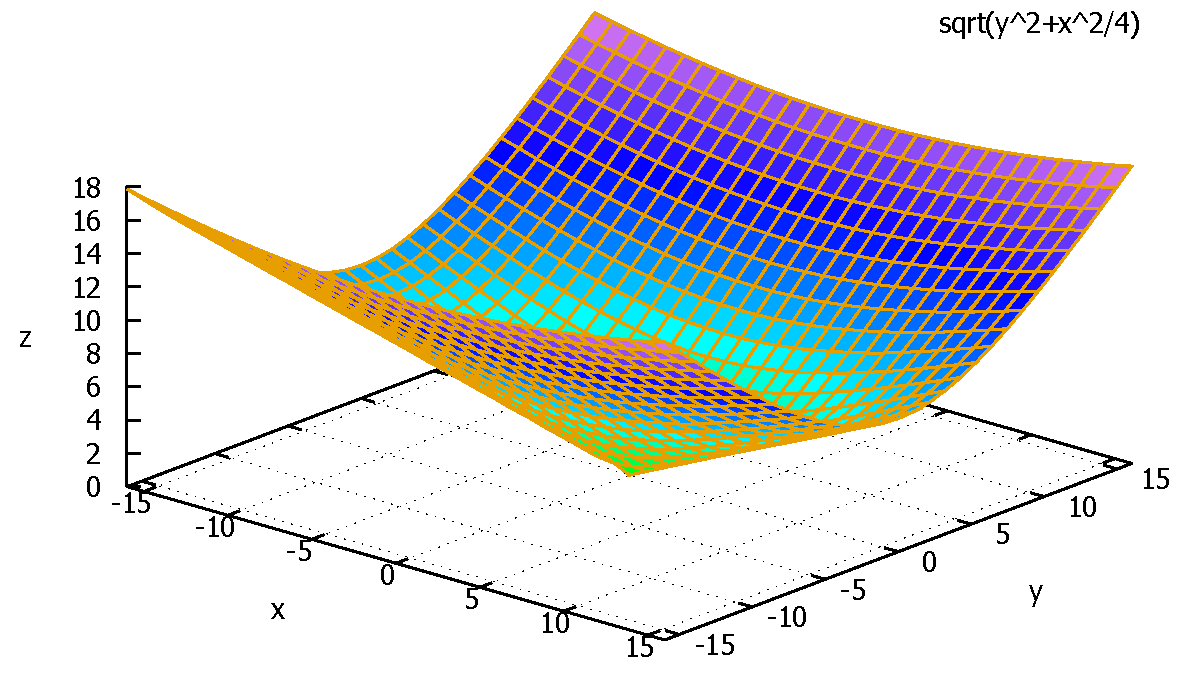
fig5 \(\sqrt{\frac{x^2}{2^2}+\frac{y^2}{1}}\)
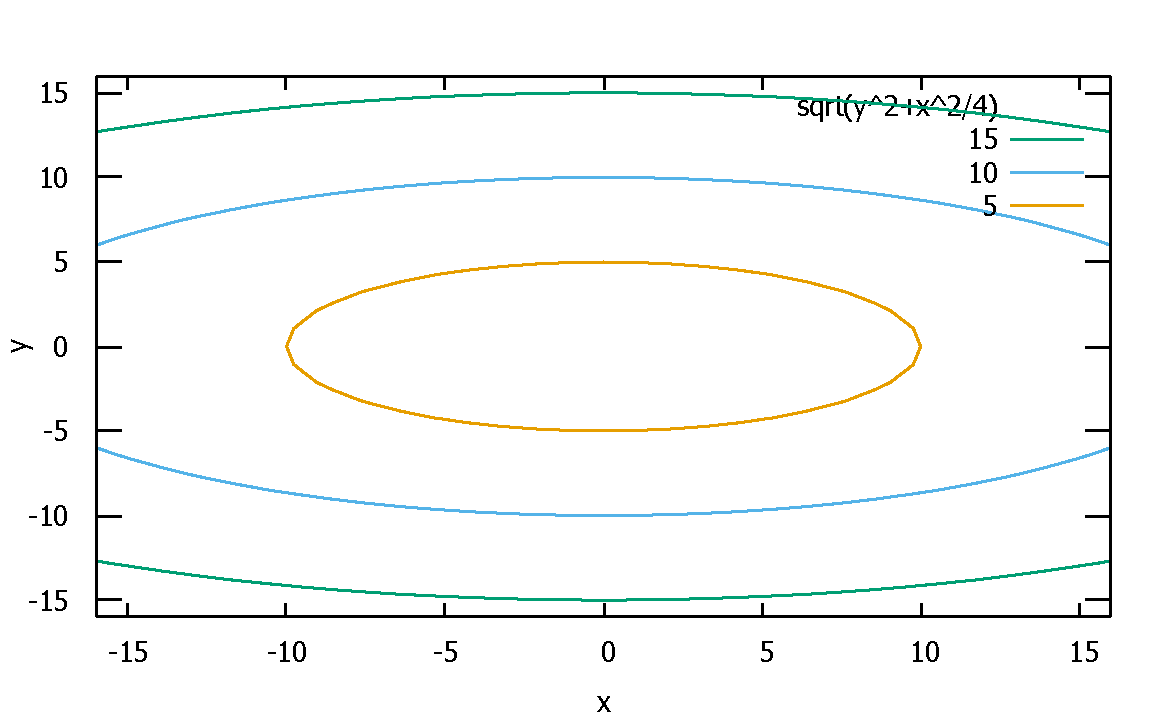
fig6 等高図
\(z=\frac{3}{x^2+y^2+2}\) のy軸に垂直な面の切り口を求める
切り口の曲線は:y=0 を代入し
\(z=\frac{3}{x^2+2}\) である
このグラフの概略は
\(x=0\) で最大、 \(Z_{max}=\frac{3}{2}\)
\(x \rightarrow \pm \infty \) で \(z\rightarrow 0\) に収束。
(fig7 ではx の小さい領域なので確認できない)
正確にはzの1回微分、2回微分から曲線の極値、変曲点、増減を調べる。(ここでは省略する)
x軸に垂直な面の切り口も同様な式が求まるので、等高線は円であると想定できる。
(\(z=\frac{3}{y^2+2}\))
そこで式を変形すると、等高線は円であることが分かる。
\(1=\frac{3}{x^2+y^2+2}\) \(\rightarrow 1=x^2+y^2\)
∴与式は z軸を頂点(最大)にして末広がりに減少していく曲面である。
(末広がりである富士山のイメージです)
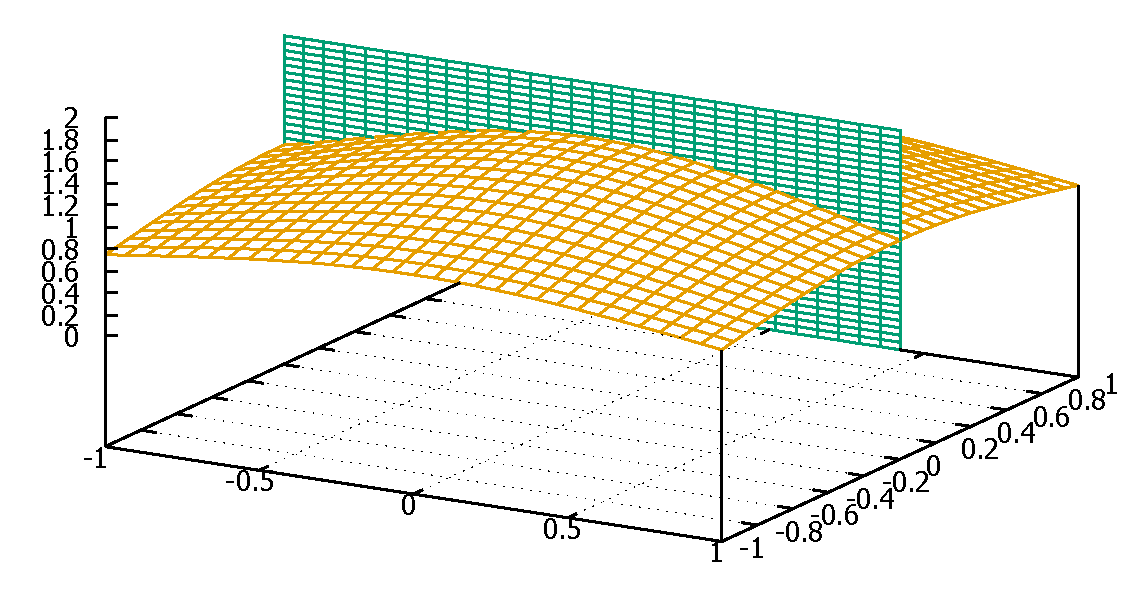
fig7 \(\frac{3}{x^2+y^2+2}\)
2変数関数の連続性については、上記の「2変数関数の極限」の内容とよく似ている。
2変数関数の連続性
\(xy\)平面の\(D\)上で定義された2変数関数、\(f(x,y)\)が\((a,b)\)で連続であるとは
\(\displaystyle \lim_{(x,y) \to (a,b)} f(x,y)=f(a,b) \)
が成り立つことである。
これを\(ε-\delta\)論法でいうと
\(xy\)平面の\(D\)上で定義された2変数関数について
\( \forall ε\gt 0 \quad \exists δ \quad s.t.\)
\( (\forall(x,y)\in D)\) \(,\) \( (0 \lt \sqrt{(x-a)^2 + (y-b)^2} \lt \delta) \)
\(\Rightarrow |f(x,y)-f(a,b)|\lt ε\)
のとき、
\(\displaystyle \lim_{(x,y) \to (a,b)} f(x,y)=f(a,b) \)
がいえる。
|
例題1、2において極限値を求めたが、2変数関数の点(a,b)に極限があれば連続である。
連続性を調べることは極限を調べることである。
次回は偏微分に進みます。