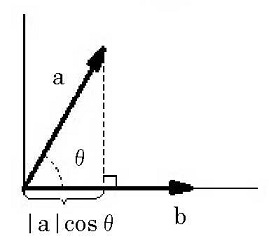
\(|a|cosθ\)はベクトルa のベクトルb 方向への射影ともいいます。
(ベクトルbが地面に、ベクトルaは空中に(地面との射角θ)、a 真上の太陽光によりできる影です)
ベクトルa とb のなす角θは:
\(cosθ=\frac{a・b}{|a|\ |b|} \)
\( |a|\ |b| ≥ a \cdot b \) ( \( \because\) cosθは 1以下 )
\(a,b\)が共に単位ベクトル(長さが1)であるとき:
・a・b = 1 ⇔ θ=0
・
a ・ b = 0 ⇔ aとbが互いに直交(\(a\perp b\))
(このことは頻繁に使う性質です。)
正規直交座標\((e_1,e_2,e_3)\)の基底(単位ベクトル)が互いに直交とは:
➀
\(
\begin{eqnarray}
e_i \cdot e_j
=
\begin{cases}
1 & i=j \\
0 & i≠j
\end{cases}
\end{eqnarray}
\)
ここで次のクロネッカーのデルタを使います。
\(
\begin{eqnarray}
δ_{ij}
=
\begin{cases}
1 & i=j \\
0 & i≠j
\end{cases}
\end{eqnarray}
\)
これより、➀の2式から1式にまとまります。
\(e_i \cdot e_j=δ_{ij}\)
ベクトル\(a(a_1,a_2,a_3)\)の大きさ\(|a|\)は一般的に:
\(| a|=\sqrt{a_1^2+a_2^2+a_3^2} \)
(ベクトルには始点と終点があるから、上式は2点間の距離でもある)
以上が一般的な内積の説明でした。