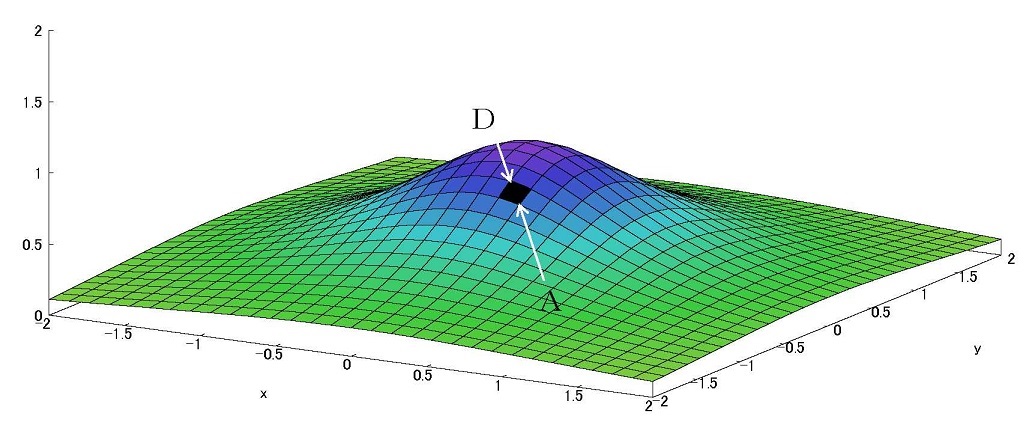
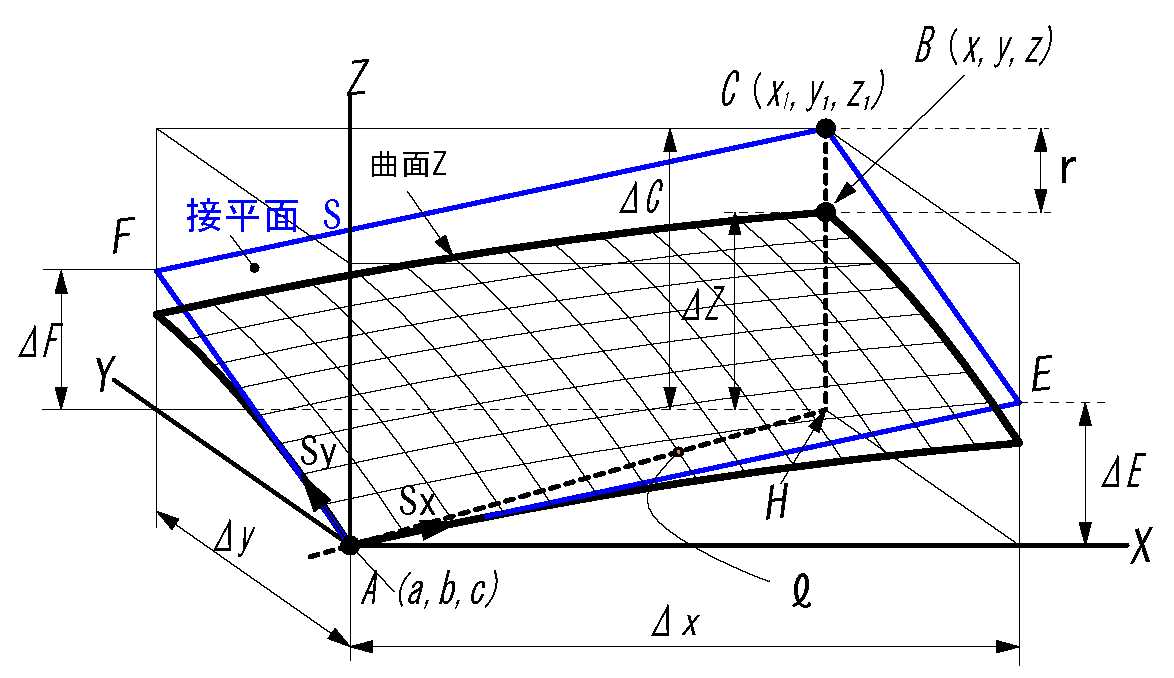
\( s_x ,\ s_y \) は単位接線ベクトル, その成分は\( s_x=(1,0,m_x), s_y=(0,1,m_y) \), また \( m_x, m_y \)は傾きです。
単位接線ベクトル\( s_x\) は 接平面の y を固定し、x 断面の x = 1 のときの Z 方向への進み量 \(m_x\) を表す。
\( s_y\) は 接平面の x を固定し、y 断面の y =1 のときの Z 方向への進み量 \(m_y\) を表す。
\(m_x\)、\(m_y\) は次式の通り、
偏微分係数です。
上式の偏微分係数は関数\(f(x,y)\)を x または y を偏微分して (x,y) に (a,b) を代入することに注意。
1変数(平面)の「曲線の
接線」に対し
2変数(空間)の場合は「曲面の
接平面」が対応します。
次式は\(f(a,b,c)\)を通る接平面の方程式
公式です。
導出は
【(※1)】を参照
\(
f(x,y)-f(a,b) \)
\(
=\frac{\partial f(a,b)}{\partial x}(x-a)\) \(+\frac{\partial f(a,b)}{\partial y}(y-b)\)
\( \dots (1) \)
・この接平面は\( S_x\) と \(S_y\) が張る平面です。
・接平面となる条件は\(f(x,y,z)\)が\((a,b,c)\)で全微分可能であること。
全微分可能とは偏微分\( f_x\) と \(f_y\)が存在し、それらが連続であること。
詳細は下記の
【(※2)】を参照
接平面の方程式
\(
f(x,y)-f(a,b) \)
\(
=f_x(a,b)(x-a) + f_y(a,b)(y-b)
\)
\(= z-c\)
\(= m_x(x-a) + m_y(y-b)\)
\(=\varDelta z\)
\( \dots (2) \)
接平面上の任意の点(\(a,b,c\))とし、任意の点が作るベクトル \( P=(x-a,\ y-b,\ z-c )\)を考える。
\( S_x\) と \(S_y\)の外積が次式の法線ベクトル\(n \ \)を作ります。
(\(n \ \)は\( S_x\) と\(S_y\)に直角)
\( n=S_x \times S_y\)
法線ベクトル\(n \ \)と接平面\(S\ \) は互いに直角です。
(また「直交する2つのベクトルの内積は「0」である」を使う)
法線ベクトル\(n \ \)とベクトル\(P \) の内積は「0」であるから次の式展開が成り立ちます。
【外積の参考先】
【内積の参考先】
( \( s_x=(1,0,m_x), s_y=(0,1,m_y) )\)
[外積計算]
\( n=S_x \times S_y\)
\(=
\left(
\begin{array}{c}
1 \\
0 \\
f_x
\end{array}
\right)
\)
\( \times\)
\(
\left(
\begin{array}{c}
0 \\
1 \\
f_y
\end{array}
\right)
\)
\(=
\left(
\begin{array}{c}
-f_x \\
-f_y \\
1
\end{array}
\right)
\)
[内積計算]
\( P \cdot n\)
\( = (x-a,\ y-b,\ z-c ) \cdot \)
\(
\left(
\begin{array}{c}
-f_x \\
-f_y \\
1
\end{array}
\right)
\)
\( = -(x-a)f_x - (y-b)f_y +(z-c) = 0\)
\(\therefore z-c=(x-a)f_x + (y-b)f_y \) \( \cdots (2)'\)
( 表記は違うけど \((2)=(2)'\) です。)