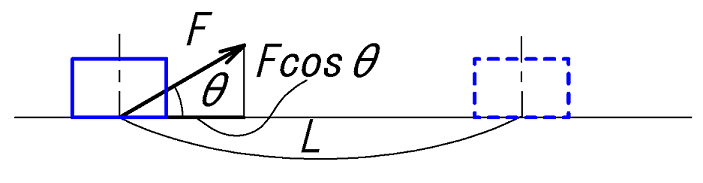
その無駄電流は「抵抗のある電線」に流れ、熱が発生し、外部に放出される、エネルギーの損失を起こします。
超電導電線(電気抵抗がない)が実現されれば熱の発生なくエネルギーの損失を起こしませんね!
(\(θ\) を位相角といい、家庭や工場で使っている電気機器・装置により決まります。 )
\(\displaystyle \int_{C} \ \bv{F} \cdot \bv{u} ds\) \(=\displaystyle \int_{C} \ \bv{F} \cdot d\bv{r}\) \(=\displaystyle \int_{a}^{b} \ \bv{F} \cdot \frac{d\bv{r}}{ds} ds\)
・\(\bv{u}=\frac{d\bv{r}}{ds}\): 単位接線ベクトル
・\(\bv{r}\): 位置ベクトル
・\(s\): 弧長パラメータ
・\(t\): 一般パラメータ
\(F_u\) は \(\bv{F}\)の曲線Cの接線方向の成分とすると:
\(F_u=\bv{F} \cdot \bv{u}\)
上式は次式で表せる。
\(\displaystyle \int_{C} \ \bv{F} \cdot \bv{u} ds\) \(=\displaystyle \int_{c} \ F_u ds\)
被積分項はベクトル場\(\bv{F}\) と単位接線ベクトル\(\bv{u}\) の内積であり、ベクトル場の線積分は 複雑な動きをする 物体の(微小)仕事の総和を示している。
\(f(x)=\color{red}{f'(a)}(x-a)+f(a)\)でした。
\(\color{red}{f'(a)}\)は「x の単位長"1"あたりのy の進み長」すなわち\(f(a)\)における単位接線です。
単位接線ベクトルは1階微分の\(f'(a)\)に相当します。
そして\(\color{red}{f'(a)}\)は次式で表せた。
\(\color{red}{f'(a)}=\displaystyle \lim_{h \to 0}=\frac{f(a+h)-f(a)}{h}\)
\(=\displaystyle \lim_{x \to a}\frac{f(x)-f(a)}{(x-a)}\)
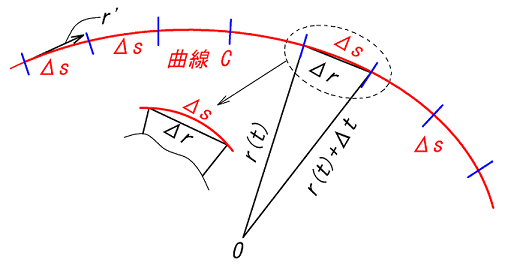
次にベクトル場の線積分の各式を導くために使う式を示します。
本によって用いてしる式が異なります。(参考にして下さい)
ベクトル場の線積分に関連する式
曲線の接線の式❶ より
・\(\bv{u}=\frac{\bv{r}'(t)}{|\bv{r}'(t)|}\) \(\ (b)\)
単位接線ベクトル\(\bv{u}\)は上記のようにベクトル\(\bv{r}'\)を自分自身の大きさで割ったものをいう。
本によっては \(\bv{t}\) を使っているが、ここでは一般パラメータ\(t\) と明確に区別するため\(\bv{u}\) とした。
曲線の長さの公式【参照先】
\(L=\int_a^b \sqrt{ (\frac{dx}{dt})^2 +(\frac{dy}{dt})^2 }\ dt\)
すなわち
\( s=\int_a^b \sqrt{ |x'(t)^2 +y'(t)^2|} \ dt\)
\(=\int_a^b \sqrt{ |r(t)^2| }dt\)
(\(ds=\sqrt{|r(t)^2|}ds\))
これより
\(\frac{ds}{dt}=|\bv{r}'(t)|\)
\(\ (d)\)
∵ここで\(\bv{r}\) を考えて、次のように\(s\)で微分する。
\(\frac{ d\bv{r}}{ds}=\frac{d\bv{r}(t)}{dt}\frac{dt}{ds}\)
\(=\bv{r}'(t) \frac{1}{|\bv{r}'(t)|}\)\(=\bv{u}\)
\(r(s)=(x(s),y(s))\)として、上式の成分表示は明らかである。
・\(d\bv{s}=\bv{u} ds\) \(\ (h)\)
\(\int_{c}\ F_u ds\)
\(=\int_{c}\ \bv{F} \cdot d\bv{r}ds\)
\(=\int_{c} \ \bv{F} \cdot \bv{u} ds\)
\(=\int_{c} \ \bv{F} \cdot d\bv{s}\)
\(\ (i)\)
\(\underline{\int_{c} \ \bv{F}(s) \cdot \bv{u} ds}\)
\(= \int_{c} \ \bv{F}(s) \cdot \frac{d\bv{r}}{ds} ds\)
\(=\int_{c} \ \bv{F}(t) \cdot \frac{d\bv{r}(t)}{dt}\frac{dt}{ds} ds\)
\(=\underline{ \int_{c} \ \bv{F}(t) \cdot \frac{d\bv{r}(t)}{dt} dt }\)
\(\ (j)\)
\(\displaystyle \int_{c} \ \bv{F} \cdot \bv{u} ds\)
\(=\displaystyle \int_{c} \ \bv{F} \cdot \frac{d\bv{r}(t)}{dt} dt\)\(\ ❷\)
\(\displaystyle \int_{c} \ \bv{F} \cdot \bv{u} ds\)
\(=\displaystyle \int_{c} \ \bv{F} \cdot \frac{ d\bv{r'(t)}} {|r'(t)|} ds\) \(\ ❸\)
\(=\displaystyle \int_{c} \ \bv{F} \cdot \frac{ d\bv{r}(s) }{ds} ds \) \(\ ❸’\)
\( \int_{c} \ \bv{F} \cdot \frac{d\bv{r}(s)}{ds} ds\)
\(=\int_{c} \ (F_x,F_y) \cdot (\frac{dx}{ds},\frac{dy}{ds}) ds\)
\(=\int_{c}(F_x(x,y)\frac{dx}{ds} + F_y(x,y)\frac{dy}{ds})ds\)
以上より
\(\displaystyle \int_{c} \ \bv{F} \cdot \bv{u} ds\)
\(=\displaystyle \int_{c} \left( F_x(x,y)dx + F_y(x,y)dy \right) \) \(\ ❹\)
\(\displaystyle \int_{c} \ \bv{F} \cdot \bv{u} ds\) \(=\displaystyle \int_{c} \left( F_x(x,y,z)dx\right.\) \(\left. + F_y(x,y,z)dy + F_z(x,y,z)dz \right) \)\(\ ❹’\)
(e')より\(\displaystyle \int_{c} \ \bv{F} \cdot \bv{u} ds\) \(=\displaystyle \int_{c} \ \bv{F} \cdot d\bv{r}\) \(\ ❺\)
\(\displaystyle \int_{-C} \ f(x,y)\ ds\) \(=-\displaystyle \int_{C} \ f(x,y)\ ds\)
\(\displaystyle \int_{C} \ f(x,y)\ ds\) \(=\displaystyle \int_{C_1} \ f(x,y)\ ds\) \(+\displaystyle \int_{C_2} \ f(x,y)\ ds\) \(+\cdots\) \(+\displaystyle \int_{C_n} \ f(x,y)\ ds\))
\(\int_{c} \ \bv{F} \cdot \bv{u} ds\)
\(=\int_{c} \ \bv{F} \cdot \frac{d\bv{r'}(t)}{|\bv{r}'(t)|} |\bv{r}'(t)|dt\)
\(=\int_{c} \ \bv{F} \cdot \bv{r'}(t)dt\)
\(=\int_{c} \ (2t+1,2t^2) \cdot (1,2) dt\)
\(=\int_c \color{red}{(2t+1 + 4t^2)dt} \)
\(=16+\frac{2}{3}\)
考察:式の展開の結果、式❷による計算結果となりました。
(途中計算でsが登場するだけ、実質はパラメータt を使っています。)
\(F=(2x+1,xy)=(2t+1,\ t^3)\)
\( \int_c (F \cdot \frac{dr}{dt})dt\)
\(=\int_c ((2t+1,\ t^3) \cdot (1,\ 2t))dt\)
\(=\int_c (2t+1 + 2t^4)dt \)
\(=\left[t^2+t+\frac{2}{5}t^5 \right]_0^2 \)
\(=(4+2+\frac{2}{5}32)\)\(=18+\frac{4}{5}\)
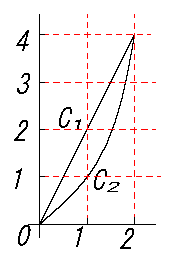
\(F(x,y)=1+y^2,2xy\) \(\quad \)
\(C_1:y=2x\) \(\ (0\le x \le 2)\)
\(C_2:y=x^2\) \(\ (0\le x \le 2)\)
\(\int_{c_1} \bv{F} \cdot \bv{u} ds\)
\(= \int_{c_1} ( (1+y^2)dx + 2xy dy)\)
\(= \int_{c_1} ( (1+(2x)^2)dx + 2x(2x)2dx) \)
\(= \int_{c_1} ( dx +4x^2dx +8x^2dx)\)
\(= \int_{c_1} ( dx +12x^2dx )\)
\(= \left[x + \frac{12}{3}x^3\right]_0^2\)
\(=2+4\cdot8\)\(=34\)
\(\int_{c_2} \bv{F} \cdot \bv{u} ds\) \(= \int_{c_1} ( (1+y^2)dx + 2xy dx)\)
\(= \int_{c_2} ( (1+(x^2)^2)dx + 2x(x^2)2xdx)\)
\(= \int_{c_1} ( dx +x^4dx +4x^4dx)\) \(= \int_{c_1} ( dx + 5x^4dx )\)
\(= \left[x + \frac{5}{5}x^5\right]_0^2\) \(=2+32\)\(=34\)
\(\phi(x,y)=x+xy^2\) とすると
\(F=grad\ \phi= (\pder{\phi}{x},\pder{\phi}{y}) \) \(=(1+y^2, 2xy) \)
山登りはポテンシャルエネルギーである重力に逆らって移動する行動です。
山登りを最大傾斜(最短)で登る経路、くねくね曲がり登る経路のどちらの経路をとっても勾配ベクトル場の線積分の値(仕事量)は変わりません。(後述します)
\(F=grad\ \phi=∇\phi\) のときの線積分:
\(\displaystyle \int_{a}^{b} \bv{F} \cdot \bv{u} ds\)
\(=\displaystyle \int_{a}^{b} ∇\phi \cdot \bv{u} ds\) \(\ ❻\)
下線部は\(\phi\) の全微分\(d\phi\)、 その積分は\(\phi\) ですね。
\(d \phi=\pder{\phi}{x}dx+\pder{\phi}{y}dy+\pder{\phi}{z}dz \)
\(\bv{F}=-∇\phi=-(\pder{\phi}{x},\pder{\phi}{y},\pder{\phi}{z})\)\(=(0,0,-mg)\)
\(d\bv{r}=(dx,dy,dz)\)
\(W=\int_{c} \bv{F} \cdot \bv{u} ds\)\(=\int_{c} \bv{F} \cdot d\bv{r}\)
\(=\int_{a}^{b} ( (0,0,-mg)\)\(\cdot (dx,dy,dz) )\)
\(=-\int_{a}^{b} mgdy\)
\(=- \left[ mgz \right]_{a}^{b}\)\(=-mg( z(b)-z(a))=-mgh\)
(\(h=z(b)-z(a)\))
この線積分は経路によらず、高さにより決まるので万有引力(重力)は保存力です。

スカラーとベクトルの掛け算はベクトルの各成分をスカラー倍。
(スカラーは単なる数(実数)です。)
ベクトル同士の加減算は各成分を単に加減すればよい。