\(\color{red}{grad\ f(\b{r})=∇\ f}\) \(= ( \pder{f(x,y)}{x},\pder{f(x,y)}{y} )\) \(\ : ❶\)
上式を次のように表すことがある。
\(∇\ f=( \pder{f}{x}\mathbb{i}+\pder{f)}{y}\mathbb{j})\)
\(\mathbb{i},\mathbb{j}\)は基底ベクトル(直行座標における)
\(grad\ f(\b{r})=∇\ f\) \(= (\pder{f(x,y,z)}{x},\pder{f(x,y,z)}{y},\pder{f(x,y,z)}{z}) \) \(\ : ❶'\)
上式を次のように表すことがある。
\(∇\ f=( \pder{f)}{x}\mathbb{i}+\pder{f}{y}\mathbb{j}+\pder{f)}{z}\mathbb{k})\)
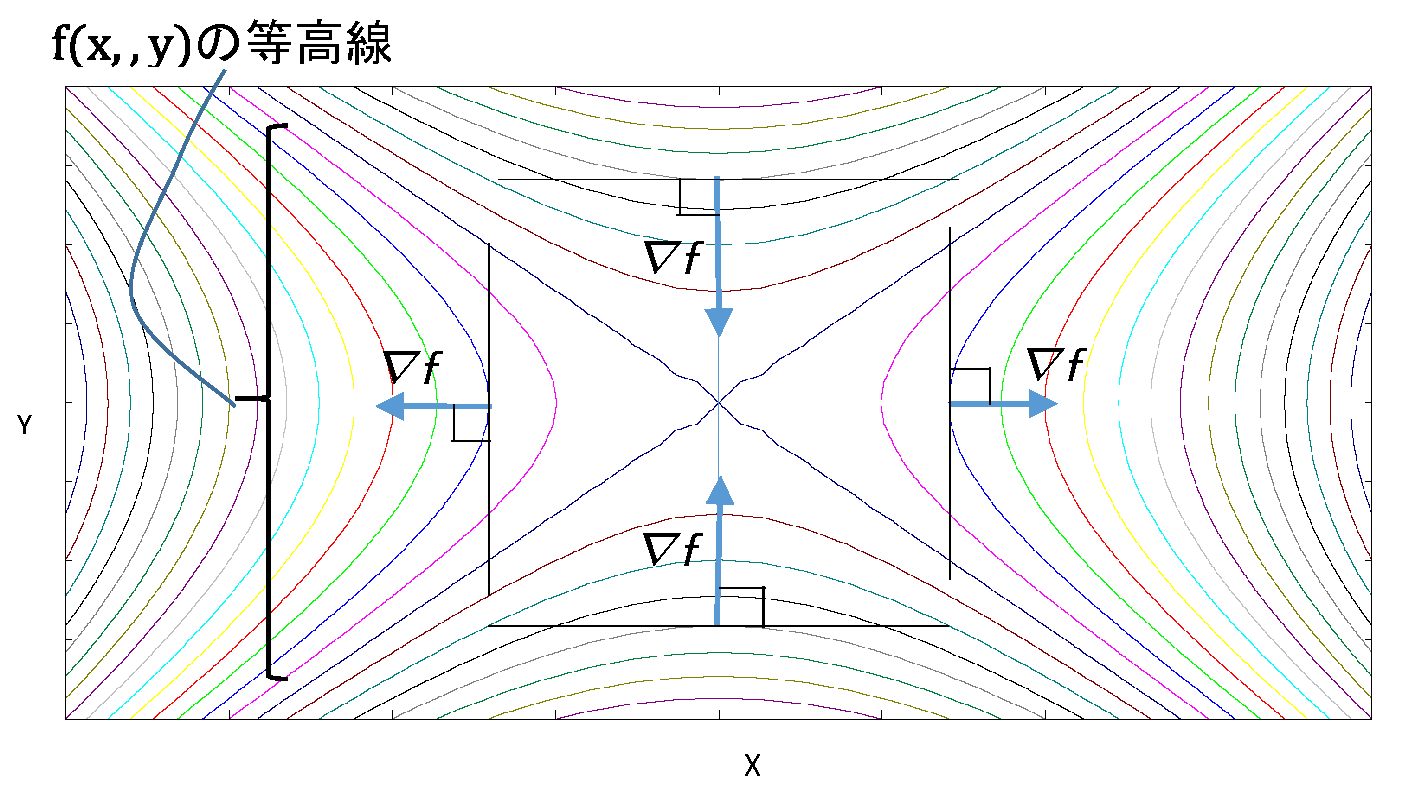
※:等高線に直交するとは、\(∇ f\) は山のような曲面で最大傾斜を向いていることを示している。
注:
スカラー場の「\( f(x,y)\)」 はスカラー(値)関数という。
ベクトル場の「\(∇\ f\)」 はベクトル(値)関数という。
・Cは定数だから以下の微分は0 です。
・媒介変数t による偏微分式です。
\(\der{}{t}[f((x(t),y(t))]\) \(=\pder{f}{x}\cdot \der{x}{t}\)\(+\pder{f}{y}\cdot \der{y}{t}=0\) \(\ : ❷\)
\((\pder{f}{x} ,\pder{f}{y}) \cdot (\der{x}{t} ,\der{y}{t})=0\) \(\ : ❸\)
\( (\pder{f}{x} ,\pder{f}{y} )\)は勾配ベクトル \(∇f\) である。
\( (\der{x}{t} ,\der{y}{t} )=r'(t)\)は等高線の接線である。
(また\(\b{A}\)と\(\b{B}\)が単位ベクトルならば
\(\b{A}\cdot \b{B}=1\)のとき、\(\b{A}\) と \(\b{B}\)は平行である。)
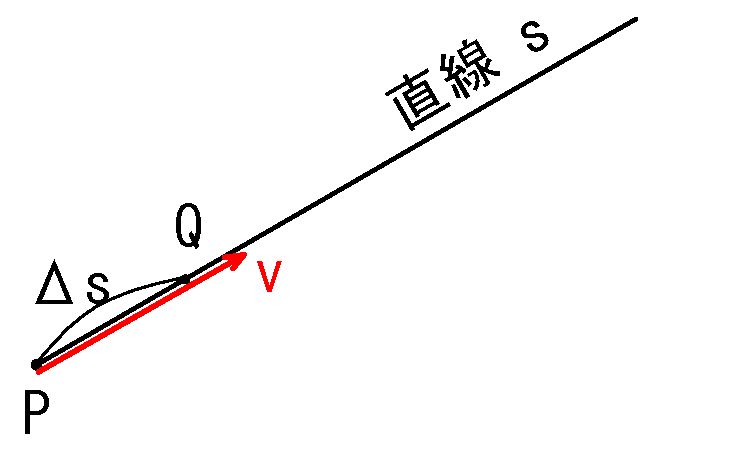
位置\(\ul{P}\)はxy座標の原点から位置ベクトル\(\ul{\b{r}}\)、位置\(\ul{Q}\)は\(\ul{\b{r}+Δs}\)にある。
・\(P=\b{r}=(x,y)\)
・\(Q=\b{r}+Δs=(x+Δs,y+Δs)\)
(参考)一般に偏微分はx についての微分と y につての微分の2つの微分式からなる。
\( f_x(x,y)=\displaystyle \lim_{ h \to a} \frac{f(x+h,y)-f(x,y)}{h}\) :\(❹_1\)
\( f_y(x,y)=\displaystyle \lim_{ k \to a} \frac{f(x,y+k)-f(x,y)}{k}\) :\(❹_2\)
方向微分係数と偏微分係数の相違
・偏微分係数はx軸とy軸についての変化率/偏微分係数です。
・方向微分係数は任意の方向ついての変化率/微分係数です。
(端的な言えば、自由な方向における偏微分のこと)
・点Pから直線\(s\)に沿って進む微小量を\(Δs\)
・\(s\)方向の単位ベクトル を\(\b{v}=(v_x,v_y)\)とする。
通常使う\(\bv{e}=(e_x,e_y)\)と識別している
・下式が方向微分係数の定義式です。
\(\underline{\displaystyle\der{f}{s}}\)\(=\displaystyle \lim_{ Δs \to 0} \frac{ \color{red}{f(x+Δs\ v_x,y+Δs\ v_y)}-f(x,y)}{Δs}\)
\(\ :❺\)
これから下式を導きだせます。
\(\der{f}{s}=\pder{f}{x}\pder{f}{y}・\b{v}\)\(=\nabla f・\b{v}\) \(\ :❻\)
\(f(x+Δs\ v_x, y+Δs\ v_y)\)\(\simeq f(x,y)+\pder{f}{x}Δs\ v_x+ +\pder{f}{y}Δs\ v_y\)
\(=f(x,y)+f_x(x,y) Δs\ v_x +f_y(x,y) Δs\ v_y \)
\(=f+f_x Δs\ v_x +f_y Δs\ v_y \)
\(\displaystyle \der{f}{s}\)
\(=\displaystyle \lim_{ Δs \to 0} \frac{f+f_x Δs v_x+f_y Δs v_y -f}{Δs}\)
\(=\displaystyle \lim_{ Δs \to 0} \frac{Δs(f_x v_x+f_y v_y)}{Δs}\)
\(=f_x v_x+f_y v_y\)
\(=(f_x f_y)\cdot (v_x, v_y)\) \(=(f_x f_y)\cdot \b{v}\) \(=(\pder{f}{x}\pder{f}{y})\cdot \b{v}\)
\(\therefore \underline{ \der{f}{s}=∇f\ \cdot \ \b{v} }\) \(\ :❻\)
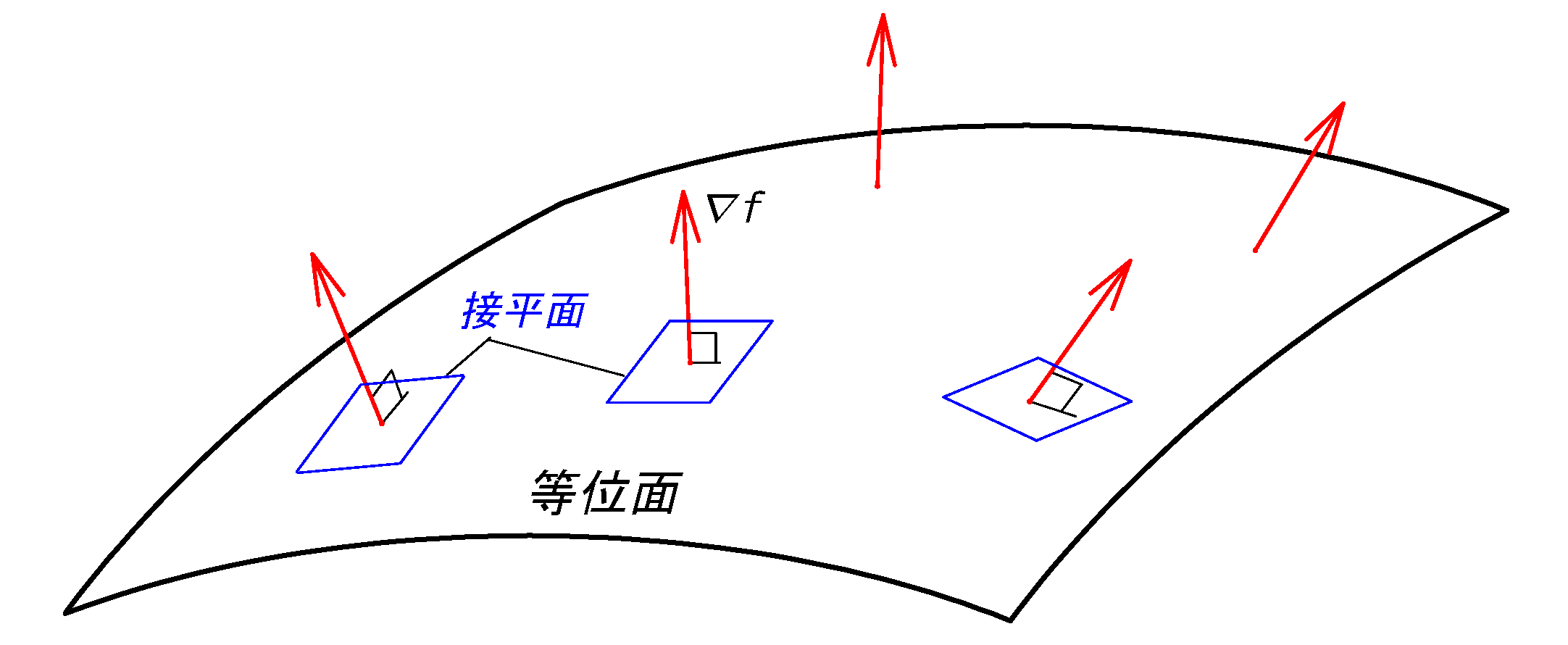
勾配ベクトル\(∇f\)は等高線に垂直。
上式は内積だから次式に展開できる。
・\(|∇f|\)と\(|\b{v}|\)が同一方向のとき\(\der{f}{s}\)が最大。
・\(|∇f|\) は方向微分 \(\der{f}{s}\) が最大となる方向を向いている。
・\(|∇f|\) は\(f\) の変化が一番大きい方向である。
\(\displaystyle \der{f}{s}\)
\(=\displaystyle \lim_{ Δs \to 0} \frac{f+f_x Δs v_x+f_y Δs v_y+f_z Δs v_z -f}{Δs}\)
\(=\displaystyle \lim_{ Δs \to 0} \frac{Δs(f_x v_x+f_y v_y+f_z v_z )}{Δs}\)
\(=f_x v_x+f_y v_y+f_z v_z \)
\(=(f_x, f_y, f_z)\cdot (v_x,v_y,v_z)\)
\(=(f_x, f_y, f_z)\cdot \b{v}\)
\(=(\pder{f}{x}\pder{f}{y} \pder{f}{z})\cdot \b{v}\)
\(=∇f\cdot \b{v}\)
\(\therefore \displaystyle \der{f}{s}\)\(=|∇f||v|cosθ\)
ベクトルの大きさをノルムという。 ノルム\(\b{v}\)を\( \| \b{v} \| \) と書く。
\(\| \b{v} \|= \sqrt{ a^2+b^2 }\)
単位ベクトルでない \(\b{v}=(a,b)\) を単位ベクトルに変換する式は:
\(\der{f}{s}\)\(=\displaystyle \lim_{ Δs \to 0} \frac{ f(a+Δs\ v_x,b+Δs\ v_y)-f(a,b) }{Δs}\):❺
\(a+Δs v_x=1+Δs \frac{\sqrt{3}}{2}\)
\(b+Δs v_y=0+Δs \frac{1}{2}\)
\(\der{f}{v}\)
\(=\displaystyle \lim_{ Δs \to 0} \frac{1}{Δs} [(f(1+Δs \frac{\sqrt{3}}{2},Δs \frac{1}{2})-f(1,0)] \)
上記のx と y 成分を与式に代入
\(=\displaystyle \lim_{ Δs \to 0} \frac{1}{Δs} [(1+\frac{\sqrt{3}}{2})^2 -2(\frac{1}{2}Δs)^2 -1] \)
\(=\displaystyle \lim_{ Δs \to 0} \frac{1}{Δs} [(1+\sqrt{3}Δs+\frac{3}{4}Δs^2)-(\frac{1}{2}Δs^2)-1]\)
\(=\displaystyle \lim_{ Δs \to 0} \frac{1}{Δs} Δs[(\sqrt{3}+\frac{1}{4}Δs)] \)
\(=\displaystyle \lim_{ Δs \to 0} (\sqrt{3}+\frac{1}{4}Δs) \)
\(=\sqrt{3}\)

\(g=-\pder{}{x}\phi(x)\) \(=-∇\phi=-grad\ \phi\)
\(f=mg(x)=-m∇\phi=-m\ grad\ \phi\)
\(E=-\pder{}{x}\phi(r)=-∇\phi=-grad\ \phi \)
\(f=qE(r)=-q∇\phi=-q\ grad\ \phi \)