定積分5/曲線の長さ

 --目　次--
∗媒介変数の関数による
∗関数\(fx)\)による
∗極方程式の関数による
∗例題1：円周
∗例題2：サイクロイド曲線
∗例題3：インボリュート曲線
∗例題4：\(y=\frac{1}{2}x^2\)
∗例題5：\(r=1+sinθ \)

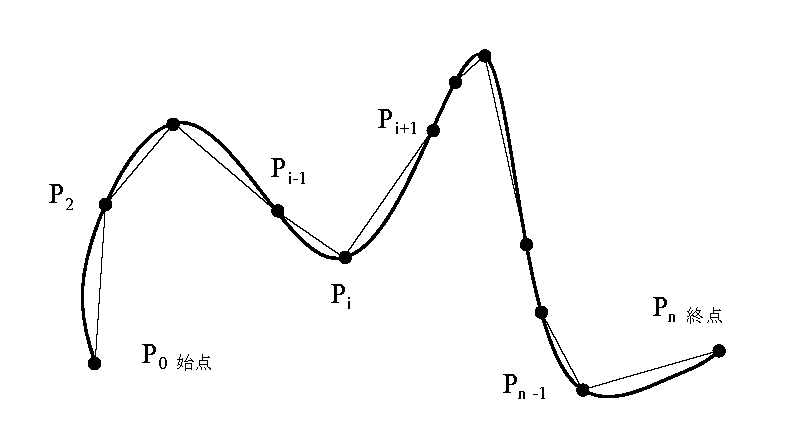
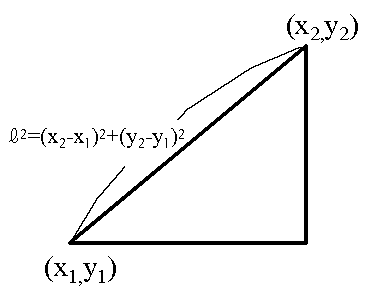 図のように 曲線C を折れ線で近似します。
リーマン積分と同様にt の閉区間[a,b] のΔ分割を考えます。
\(Δ :\ a(P_0)=t_0<t_1<t_2<…t_i<\) \(…t_{n-1}<t_n=b(P_n)\)

\(Δ\) の\(t_i\) に対応し、C上にできる\(n-1\)個の分点 「\(P_0(t_0),P_1(t_1),\cdots ,P_n(t_n)\)」 を結んでできる折れ線が 曲線\(C\) に近似できる。

２点間の距離は次式で求められる。（fig2）
（3平方の定理より）
\(\ell_i=\ell(\Delta_i)\)\(=P_{i-1}P_i\)\(=\sqrt{ [x(t_i)-x(t_{i-1})]^2 + [y(t_i)-y(t_{i-1})]^2 }\) ：❶

閉区間での曲線の長さの近似は：
\(　L(\Delta)\)\(=\displaystyle \sum_{i=1}^{n} \sqrt{ (x(t_i)-x(t_{i-1}))^2 + (y(t_i)-y(t_{i-1}))^2 }\)

上式を変形すると：
\(=\displaystyle \sum_{i=1}^{n} \frac{ \sqrt{ (x(t_i)-x(t_{i-1}))^2 + (y(t_i)-y(t_{i-1}))^2}}{t_i-t_{i-1}} (t_i-t_{i-1}) \)

\(\therefore \) \(L(\Delta)\)\(=\displaystyle \sum_{i=1}^{n} \sqrt{ \left( \frac{x(t_i)-x(t_{i-1})} {t_i-t_{i-1}} \right) ^2 + \left( \frac{y(t_i)-y(t_{i-1})} {t_i-t_{i-1}} \right) ^2 }\)\((t_i-t_{i-1}) \) :❷

根号の中は平均値の定理（ 【参照先】 ）の式と同じ形になりました。すなわち：
\(\frac{dx}{dt}(c_i)=x'(c_i)\)\(=\frac{x(t_i)-x(t_{i-1})} {t_i-t_{i-1}}\)

\(\frac{dy}{dt}(d_i)=y'(d_i)\)\(=\frac{y(t_i)-y(t_{i-1})} {t_i-t_{i-1}}　　　\)　

各分割には2点間との平均値と同じ傾きの微分係数が存在する。
x,y は微分可能なので、その導関数は連続である。
\(c_i, d_i\) は閉区間 \([t_{i-1}, t_i]\)内で任意の代表点。

\(x(t_i)-x(t_{i-1})=x'(c_i)\ (t_i-t_{i-1})\)

\(y(t_i)-y(t_{i-1})=y'(d_i)\ (t_i-t_{i-1})\)

これより、式❶は次式（❶'） に変形：
❶ \(=\sqrt{ [x'(c_i) (t_i-t_{i-1})]^2+ [y'(d_i) (t_i-t_{i-1})]^2} \)

\(\therefore \) \(\ell(\Delta_i)\)\(=\sqrt{ (x'(c_i))^2+(y'(d_i))^2 } (t_i-t_{i-1}) \) ：❶'

\(y'\) は連続だから分割\(\Delta\) を細分していけば \(c_i\) と \(d_i\) の差は小さくなり、 \(y'(c_i)\) と\(y'(dc_i)\) の差も小さくなると想定（直感）します。
これを以下で証明します。

閉区間 \([t_{i-1}, t_i]\)内で \(y'_i(t)\)の最大値、最小値を\(M_i,\ m_i\)とする。
また､\(M_i-m_i\) の差の最大値を\(\delta_{max}\) とする。

ここで分割\(\Delta_i\)における次の式を考え、変形していきます。
（式❶’をイメージに残して）
\(|\sqrt{ (x'(c_i))^2+(y'(d_i))^2 }\)\(-\sqrt{ (x'(c_i))^2+(y'(c_i))^2 }|\)　：❸　

式❸の\(x'\) を消去し、\(y'\)だけの式に変形していきます。

簡略表記のために
\(A=(x'(c_i))^2+(y'(d_i))^2 \quad\) \(B=(x'(c_i))^2+(y'(c_i))^2\) とおく。

❸\(=|\sqrt{A}-\sqrt{B}|\)
\(=|\sqrt{A}-\sqrt{B}|\times\frac{\sqrt{A}+\sqrt{B}}{\sqrt{A}+\sqrt{B}}\) \(=\frac{|A-B|}{\sqrt{A}+\sqrt{B}}\)

\(=\frac{|(x'(c_i))^2+(y'(d_i))^2 -(x'(c_i))^2-(y'(c_i))^2|}{\sqrt{A}+\sqrt{B}}\)

\(=\frac{|(y'(d_i))^2-(y'(c_i))^2|}{\sqrt{A}+\sqrt{B}}\)

\(=\frac{|y'(d_i)|+|y'(c_i)|}{\sqrt{A}+\sqrt{B}}\ |y'(d_i)-y'(c_i)| \)

\(≤\frac{|y'(d_i)|+|y'(c_i)|}{|y'(d_i)|+|y'(c_i)|}\ |y'(d_i)-y'(c_i)| \)

(\(\because \)\(\sqrt{A}+\sqrt{B}>|y'(d_i)|+|y'(c_i)|\))

\(=|y'(d_i)-y'(c_i)|\)

また\(M_i,\ m_i\)の定義より
\(|y'(d_i)-y'(c_i)|\) \(≤M_i-m_i\)\(≤\delta_{max}\)

以上から次の関係が成り立つ
\(\therefore\) \(|\sqrt{A}-\sqrt{B}|\) \(=|\sqrt{(x'(c_i))^2+(y'(d_i))^2}\)\(-\sqrt{(x'(c_i))^2+(y'(c_i))^2}|\) \(≤|y'(d_i)-y'(c_i)|\) \(≤M_i-m_i\)\(≤\delta_{max}\)

上記の結果をさらに展開する。
その前に、次式を確認しておこう。
❶’ \(=\ell(\Delta_i)=\sqrt{ (x'(c_i))^2+(y'(d_i))^2 } (t_i-t_{i-1})\) \(=\sqrt{A}(t_i-t_{i-1})\)

全閉区間\([a,\ b]\)の長さの式に拡張すべき次式を考え変形していく：
　 \(|\displaystyle \sum_i^n \ell(\Delta_i)\) \(-\displaystyle \sum_i^n \sqrt{B}\ (t_i-t_{i-1})|\)

\(=|\displaystyle \sum_i^n \sqrt{A}\ (t_i-t_{i-1}))\)\(-\displaystyle \sum_i^n \sqrt{B}\ (t_i-t_{i-1})|\)

\(≤\displaystyle \sum_i^n | (\sqrt{A}-\sqrt{B}) | \ (t_i-t_{i-1})\)

\(≤\displaystyle \sum_i^n (M_i-m_i) \ (t_i-t_{i-1})\) \(≤\displaystyle \sum_i^n \delta_{max} \ (t_i-t_{i-1})\)

\(=\delta_{max} \displaystyle \sum_i^n \ (t_i-t_{i-1})\) \(=\delta_{max}(b-a)\)

\(\therefore \) \(|\displaystyle \sum_i^n \ell(\Delta_i)\)\(-\underline{\displaystyle \sum_i^n \sqrt{B}\ (t_i-t_{i-1})} | \) \(≤\delta_{max}(b-a)\) :❹

式❹の\(n\rightarrow 0 \)の極限、すなわち分割\(\Delta\)を限りなく小さすると\(\delta_{max}\)は 0 に近づく。

そして式❹の下線部の項の極限は（ \(\sqrt{B}\)を元に戻して）：
\(\underline{\displaystyle　\lim_{n \to \infty} \displaystyle \sum_i^n \sqrt{B} (t_i-t_{i-1})}\) \(=\displaystyle \lim_{n \to \infty} \displaystyle \sum_i^n \sqrt{(x'(c_i))^2+(y'(c_i))^2} (t_i-t_{i-1})\) :❺
となる。

次の積分定義（リーマン和による）【参照先】 を見てください。
\(\int_a^b f(x) dx\)\(=\displaystyle \lim_{ |Δ| \to 0 } \displaystyle \sum_{i=1}^n f(c_i) (x_i-x_{i-1})\) ：(a)

式❺は定積分の式にほかならない。
\(\displaystyle\lim_{n \to \infty} \displaystyle \sum_i^n \sqrt{(x'(c_i))^2+(y'(c_i))^2}\)\( (t_i-t_{i-1})\) \(=\int_a^b \sqrt{(x'(t))^2+(y'(t))^2} dt\)

また、式❹の右辺は「0」、そして式❹の極限は：
\(L=\displaystyle\lim_{n \to \infty}\displaystyle \sum_i^n \ell(\Delta_i)\) \(=\displaystyle\lim_{n \to \infty} \displaystyle \sum_i^n \sqrt{B} (t_i-t_{i-1})\)

\(=\displaystyle\lim_{n \to \infty}\displaystyle \sum_i^n \sqrt{(x'(c_i))^2+(y'(c_i))^2} (t_i-t_{i-1})\)

（式(a)を参照して）
これから求める曲線の長さは：

\(\underline{ L=\int_a^b \sqrt{(x'(t))^2+(y'(t))^2} dt } \)
冒頭の媒体変数表示の曲線の長さの導出ができました。

\(\Delta \ell_i=\sqrt{ (\Delta x_i)^2+(\Delta y_i)^2}\)

\(=\sqrt{ 1+(\frac{\Delta y_i}{\Delta x_i})^2} \Delta x_i\)

今までと同様に分割Δを限りなく 0　に近付ける、すなわち\(n \rightarrow 0\)のとき：
\(\displaystyle　\lim_{n \to \infty} \displaystyle \sum_i^n \sqrt{ 1+(\frac{\Delta y_i}{\Delta x_i})^2} \Delta x_i\) \(=L\)

この式は定積分の式にほかならない。
これより曲線の長さ\(L\):
\(L=\int_a^b \sqrt{ 1+(\frac{dy}{dx})^2} dx\) \(=\int_a^b \sqrt{1+(f'(x))^2} dx\)

\(\Delta\ell \fallingdotseq \sqrt{ (rΔθ)^2+(Δ r)^2 }\) \(= \sqrt{r^2 + (\frac{Δr}{Δθ})^2 Δθ }\)

\(rΔθ\) の根拠の【参照先】

\(L=\displaystyle\lim_{n \to \infty} \displaystyle \sum_i^n \sqrt{r^2 + (\frac{Δr}{Δθ})^2} \Delta θ\)

この式は定積分に式にほかならない。
これより曲線の長さ\(L\):
\(L=\int_a^b \sqrt{ r^2 +(\frac{dr}{dθ})^2} dθ\)

\(r=f(θ)\)より
\(x=rcosθ \ , \)　\(y=rsinθ\)

\(x'=r'cosθ-rsinθ\ ,\ \) \(y'=r'sinθ+rcosθ\)

公式[1]より:
\(L=\int_a^b \sqrt{ (\frac{dx}{dt})^2 +(\frac{dy}{dt})^2 }\ dt\)　:[1]

\(L=\) \(\int_α^β \sqrt{ (r'cosθ-rsinθ)^2+(r'sinθ+rcosθ)^2} dθ\)

\(=\int_α^β \sqrt{ (r')^2 +r^2 }\ dθ\)

\(\therefore\) \(L=\int_α^β \sqrt{r^2+(\frac{dr}{dθ})^2}\ dθ\)

円の方程式： \(x^2+y^2=r^2\)
\(x=r\ cos\ t\)
\(y=r\ sin\ t\)
t の区間\([0,\ 2\pi]\)

公式[1]: \( L=\int_a^b \sqrt{ (\frac{dx}{dt})^2 +(\frac{dy}{dt})^2 }\ dt\)

\(x'(t)=-r sin t\) \(, \quad y'(t)=r cos t\)

\(L=\int_0^{2\pi} \sqrt{ (-r sin t)^2 +(r cos t )^2 }\ dt\) \(=r \int_0^{2\pi} \sqrt{ sin^2 t +cos^2 t }\ dt\)

\(=r \int_0^{2\pi} dt\) \(=r [t]_0^{2\pi}\) \(=2\pi\ r \)

媒介変数表示の関数の公式[1]を使う。

\(x'(t)=(a(t-sin t))'=a(1-cos t)\)

\(y'(t)=(a(1-cos t))'=a sin t\)

\(L=\int_0^{2\pi}\sqrt{(x'(t))^2 +(y'(t))^2 } dt\) \(=\int_0^{2\pi}\sqrt{(a(1-cos t)^2 +(a sin t )^2 }\ dt\) \(=a \int_0^{2\pi}\sqrt{1-2cos t+cos^2 t+sin^2 t }\ dt\)

\(=a \int_0^{2\pi} \sqrt{2(1-2cos t) }\ dt\)

\(=a \int_0^{2\pi}\sqrt{2\cdot 2 sin^2 \frac{t}{2}}\ dt\)

\(=a \int_0^{2\pi} 2 sin \frac{t}{2}dt \) \(=2a \int_0^{2\pi} sin \frac{t}{2}dt \)

\(=2a\cdot2 [- cos \frac{t}{2}]_0^{2\pi}\) \(=4a [1+1]=8a\)

図は\(a=1\)　の場合のサイクロイド曲線です。

\(x'(t)=a(-sin\ t + sin\ t + tcos\ t )\)\(=at cos\ t\)
\(y'(t)=a(cos\ t -cos\ t + tsin\ t )\)\(=at sin\ t\)

\(L=\int_0^{2\pi}\sqrt{(x'(t))^2 +(y'(t))^2 } dt\)
\(=\int_0^{2\pi}\ \sqrt{ (at cos\ t)^2 + (at sin\ t)^2 } dt \)
\(=a\int_0^{2\pi}\ \sqrt{ t^2(cos^2 t+ sin^2 t) } dt\)
\(=a \int_0^{2\pi}\ t dt \)

\(= \frac{1}{2} a [t^2]_0^{2\pi}\) \(=\frac{1}{2} a 4(\pi)^2\)

\(=2 a \pi^2\)

公式[2]:\(L=\int_a^b \sqrt{ 1 +(f'(x))^2 }\ dt\)

\(y'(x)=x\)

\(L=\int_0^1 \sqrt{ 1 +x^2 }\ dt\)

この積分、なかなか大変です。 【ここを参照】：
（以下は積分の結果（部分積分で解きます））
\(= [\frac{1}{2}( x \sqrt{1+x^2}\)\( +log |x+\sqrt{1+x^2}|)]_0^1 \)

\(= [\frac{\sqrt{2}}{2}+\frac{1}{2}(log |1+\sqrt{2}|-log |1|)]\)

\(\therefore\) \(L=\frac{\sqrt{2}}{2}+\frac{1}{2}log |1+\sqrt{2}|\)

公式[3]を使います
[3]:\(L=\int_\alpha^\beta \sqrt{ r^2 +(\frac{dr}{dθ})^2 } \ dθ \)

\(r'(θ)=(1+sinθ))'=cosθ\)

これを公式に代入し、計算するだけだが、計算は長くなります。

\(L=\int_0^{\pi} \sqrt{ (1+sinθ)^2 + (cosθ)^2 } \ dθ \)

\(=\int_0^{\pi} \sqrt{ 1+2sinθ+sin^2θ +cos^2θ} \ dθ \)

\(=\int_0^{\pi} \sqrt{ 2+2sinθ } \ dθ \) \(=\int_0^{\pi} \sqrt{ 2(1+sinθ)} \ dθ \) \(=\sqrt{2} \int_0^{\pi} \sqrt{ 1+sinθ} \ dθ \)

\(=\sqrt{2} \int_0^{\pi} \sqrt{ 1+cos(\frac{\pi}{2}-θ) }\ dθ \)

\(=\sqrt{2} \int_0^{\pi} \sqrt{ 2cos^2(\frac{\frac{\pi}{2}-θ}{2}) }\ dθ \)

\(=\sqrt{2} \int_0^{\pi} \sqrt{2 cos^2(\frac{\pi}{4}-\frac{θ}{2})} dθ \)

\(=2 \int_0^{\pi} \sqrt{ cos^2 (\frac{\pi}{4}-\frac{θ}{2})} dθ \)

\(=2 \int_0^{\pi} cos (\frac{\pi}{4}-\frac{θ}{2}) dθ \)

\(=2 [-2 sin (\frac{\pi}{4}-\frac{θ}{2})]_0^{\pi} \)

\(=2 [-2 sin (-\frac{\pi}{4}) + 2 sin (\frac{\pi}{4})] \)

\(=2 [\sqrt{2} + \sqrt{2}]\) \(=4 \sqrt{2}\)

 例題のサイクロイド曲線とインボリュート曲線は歯車の歯の形状（歯形という）に応用されています。
日常生活の身近なところでは 機械式時計の歯車にはサイクロイド曲線の歯車が使われ、 また自動車などの大きな動力を伝えるようなところにはインボリュート曲線の歯車が使われいます。
その理由は…これは機械工学の分野におまかせします。