エールステッドの「電流の磁気作用」の発見後, ファラデーは, 磁石をコイルに出し入れしたときに, コイルに電流が流れる電磁誘導を発見した。コイルが磁界の影響下にあるとき, コイルは何か特別な緊張した状態(電気的緊張状態:\(Electro\;tonic\;State\))になり, 磁石を動かして, 電気的緊張度を変化させると, 電流が流れると…。が, それ以上の進展はなかった。
これを引き継いだのがマクスウェルである。マックスウェルはアンペールの提唱した「磁石は微小電流の渦」との関係を考えたのであろうか?ファラデーが電磁誘導を発見した1831年に, エディンバラで生まれたマクスウェルは, 1856年, ベクトルポテンシャルこそが電気的緊張度を表す量であると考え, 力学とのアナロジーを頼りに理論を進めた。
マクスウェルの考えた電磁界・エーテル界
改めてビオ・サバールの法則 ベクトルポテンシャルを示唆?
ビオ・サバールの法則を再掲しよう。
導線上の微小な長さ\(~ds~\)を流れる電流素片\(~Ids~\)が, 距離\(~r~\)だけ離れた点に作り出す微小な磁場\(~dB~\)は
\[dB=\frac{\mu_0}{4\pi}\frac{I ds}{r^2}sin\theta\]
である。さらにこの式をベクトル表現すると電流素片\(~Id\bm{s}~\)が, そこから\(~\bm{r}~\)の位置に作る微小磁場\(~d\Vec B~\)は
\[d\Vec B=\frac{\mu_0}{4\pi}\frac{I d\bm{s}\x \bm{r}}{r^3} \]
である。これをビオ・サバールの法則と呼んだ。
この式を用いれば, 任意の形状\(~C~\)に沿って流れる電流\(~\Vec I~\)が作る磁場は
\[\Vec B=\frac{\mu_0 I}{4\pi}\int_C\frac{d\bm{s}\x \bm{r}}{r^3}=-\frac{\mu_0 I}{4\pi}\int_C d\bm{s}\x \nabla\frac{1}{r}=\nabla\x \frac{\mu_0 I}{4\pi}\int_C \frac{d\bm{s}}{r} \]
で求めることが出来る。最後は\(~d\bm{s}~\)と\(~\nabla~\)の順序を入れ替えたので符号が変わっている。また
\[\frac{\bm{r}}{r^3}=-\nabla\frac{1}{r}\]
を用いた。ベクトル表示をするために, 電流素片と磁場の位置関係を\(~\bm{r}/r^3~\)としてあるが, \(x~\)軸だけならば\(~\displaystyle\frac{1}{x^2}~\)であり, \(\displaystyle\frac{1}{x^2}=-\frac{d}{dx}\frac{1}{x} ~\)から容易に分かるだろう。さらに,
\[\Vec A(\bm{r})=\frac{\mu_0 I}{4\pi}\int_C \frac{d\bm{s}}{r}\tag{1}\]
と置くと, (電流素片の位置を\(~\bm{r'}~\)として, \(1/r~\)は\(~1/|\bm{r}-\bm{r'}|~\)とすべきだが, 本記事では分かりやすく\(~1/r~\)とした)
\[\Vec B=\nabla\x \Vec A(\bm{r})\tag{2}\]
と表せる。\(1/r=\bm{r}/r^2~\)が正確な表記だから\(\Vec A(\bm{r})~\)としてある。
史実とは異なると思うが, 以下は筆者の想像である。\(\Vec B=\nabla\x \Vec A(\bm{r})\)。マックスウェルがこの関係に気づかないはずは無い。
アンペールを電磁気学のニュートンと尊敬していたマックスウェルは, この回転が円形電流だと考えたのだろうか?
マックスウェルより以前に気づいていた学者も多い。ガウス, リーマン, ノイマン, キルヒホフなどが論文の中で電流の誘導に関して用いていた。\(W.Thomson~\)(後のケルビン卿)は1847年の論文で磁気誘導\(~\Vec B~\)と\(\Vec B=\nabla\x \Vec A~\)の関係にあるベクトル\(~\Vec A~\)を, エーテルの弾性変位と同一視できる事を指摘した。
マックスウェルの方法論 エーテルの力学
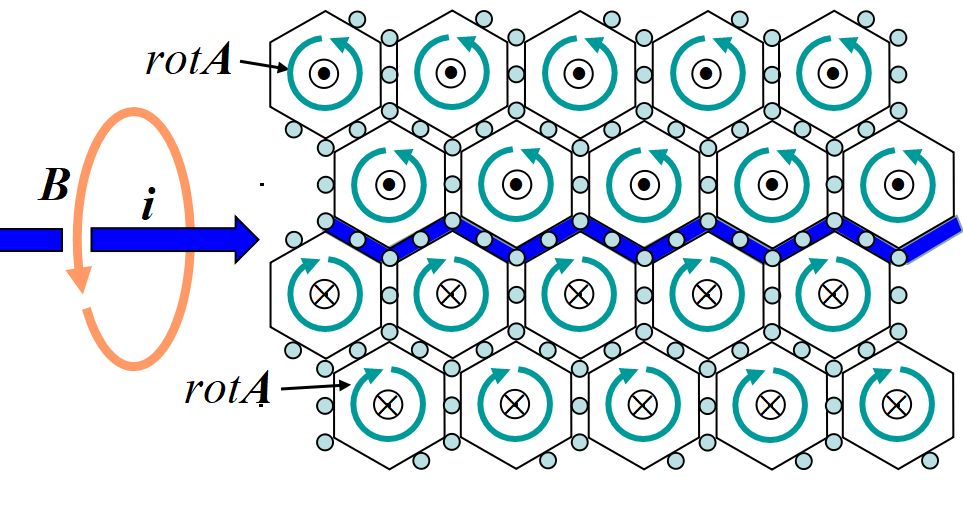
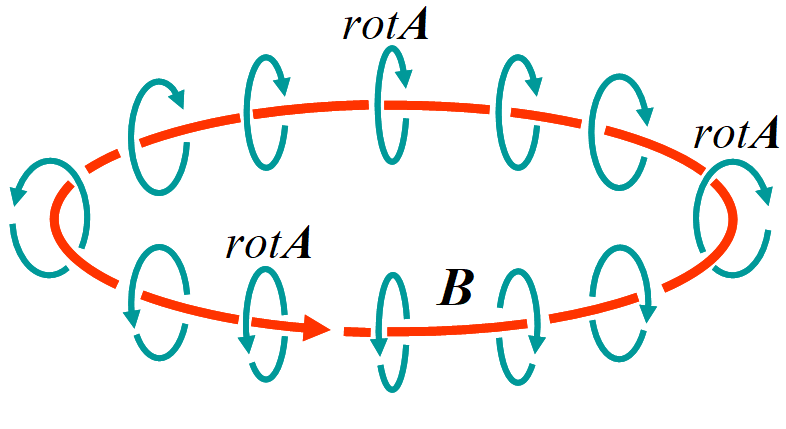
マックスウェルは, 特に初期は力学とのアナロジーを積極的に進め, 電磁気学の基礎方程式に迫って行った。図はマックスウェルのエーテルモデルで, 磁場は6角形の柱の回転(渦)である。磁場が起こると柱が回転し, 間に挟まった小球(電荷)が回転させられ移動を始める。これが電磁誘導による電流である。
逆に図の中央を, 電流が左から右に流れると, 流れに沿って電気的緊張度を表すベクトルポテンシャルが発生し, それが渦を巻いて特定の方向に並ぶ。この並ぶ方向が磁力線の向きとなる。磁力線は, 図の上半分で手前向き, 下半分では向こう向きである。
力学と電磁気学のアナロジー 電気的緊張度\(~Electro\,tonic\,State~\)
以下は, 電磁気学が力学, 特にエーテル力学を拠り所として発展してきたことを示すのが目的で, いささか正確性に欠ける。
詳しくはFNの高校物理, または原著「電磁場の動力学」(1865年マックスウェル)を参照されたい。
ベクトルポテンシャルが導入されている。またマックスウェルが電気力学的運動量 (\(Electrokinetic\;momentum~\))と名付けた理由が良く分かる。
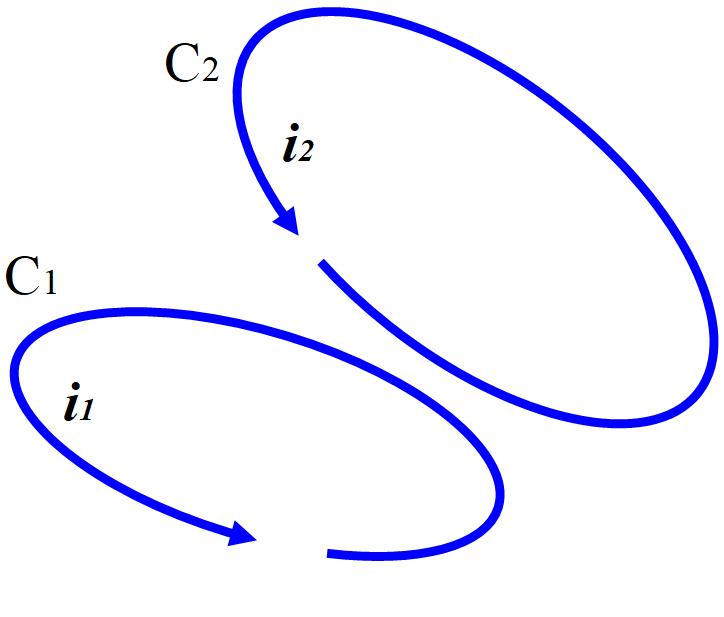
図のような2つの回路に電流\(~\bm{i}_1,\,~\bm{i}_2~\)が流れているとすると, この系のエネルギーは
\[\mathcal{L}=\frac{1}{2}L_1i_1^2+\frac{1}{2}L_2i_2^2+Mi_1i_2\]
と書ける。\(L_k~\)は自己誘導係数, \(M~\)は相互誘導係数である。
マックスウェルは電流を速度になぞらえて\(~\dot{y}~\)と書き
\[\mathcal{L}=\frac{1}{2}L_1\dot{y_1}^2+\frac{1}{2}L_2\dot{y_2}^2 +M\dot{y_1}\dot{y_2} \]
を力学のラグラジアンに見立てて, 運動量を
\[p_k=\dd{\mathcal{L}}{t}\]
と考えた。すなわち
\[p_1=L_1\dot{y_1}+M\dot{y_2},\qquad p_2=L_2\dot{y_2}+M\dot{y_1} \]
である。ただしこれは力学での運動量とは異なるので
電磁的運動量 (\(Electromagnetic\;momentum~\))と呼んだ。
さらに8年後には
電気力学的運動量(\(Electrokinetic\;momentum~\))と名称を変え, 力学的色彩が更に強まった。
電流\(~\dot{y_1}~\)を変化させたとき\(~p_2~\)に働く力は, 運動量の時間微分で
\[X_2=\frac{dp_2}{dt}=\frac{d}{dt}(M\dot{y_1})\]
となる。これも力学で言う力ではないが, 電磁誘導による起電「力」を与えると解釈する。
回路1を回路2に近づけたり, 遠ざけたりしても, あるいは回路1を変形しても\(~M~\)が変化し, やはり\(~p_2~\)に働く起電「力」が生じる。
これを現代風に書けば, 相互誘導係数は
\[M=\frac{\mu}{4\pi}\int_{C_1}\int_{C_2}\frac{d\bm{r}_1\cdot d\bm{r}_2}{|\bm{r_2}-\bm{r_1}|} \]
で与えられる。\(\bm{r}_k~\)は回路\(~C_k~\)上の位置を表し, \(d\bm{r}_k~\)は線素片, 積分は夫々の回路を一周するように行う。これに電流\(~i_1~\)をかければ
\[\Vec A(\bm{r}_2)=\frac{d}{dt}\int_{C_1}\frac{i_1d\bm{r}_1}{|\bm{r_2}-\bm{r_1}|} \]
は回路\(~C_1~\)を流れる電流\(~i_1~\)が回路\(~C_2~\)上に作るベクトルポテンシャルである。これを用いると「力」\(X_2~\)は,
\[X_2=\frac{d}{dt}\int_{C_2}\Vec A(\bm{r}_2)\cdot d\bm{r}_2 \]
となる。この線積分をストークスの定理を用いて面積分にすると
\[X_2=\frac{d}{dt}\int_{S_2}\{rot_2\Vec A(\bm{r}_2)\}\cdot d\Vec S_2 \]
となる。\(rot_2~\)は変数\(~\bm{r}_2~\)に関する\(~rot\)であり, \(d\bm{S}_2~\)は面\(~S_2~\)の面素片の面積を大きさとし, 法線方向を向いたベクトルである。
\(rot_2\Vec A(\bm{r}_2)~\)は位置\(~\bm{r}_2~\)における磁束密度\(~\Vec B(\bm{r}_2)~ \)に等しいから
\[X_2=\frac{d}{dt}\int_{S_2}\Vec B(\bm{r}_2)\cdot d\Vec S_2 \]
となり, 電磁誘導の法則により, これは回路\(~C_2~\)に誘導される起電力\(~V_2~\)に等しい。
このようにして力学とのアナロジーを進め, \(\Vec A~\)を電磁的運動量と呼び, これから力を
\[\Vec E=-\dd{\Vec A }{t}\]
によって定義する。ニュートンの運動方程式「運動量の時間微分が力に等しい」に対応する。さらに
\[\int_C\Vec E(\bm{r})\cdot d\bm{r}=-\frac{d}{dt}\int_C\Vec A(\bm{r})\cdot d\bm{r}\]
と組み合わせて,
\[\Vec E=-\dd{\Vec A}{t}-grad\Psi \]
を導いた。最後の式は, 現代では
電磁ポテンシャルとして, 量子力学で一般的に用いられている手法である。
ベクトルポテンシャル 力学のアナロジーを離れて
現代では, 電気的緊張度\(~Electro\;tonic\;State~\)からではなく, 以下のような方法が一般的である。
ファインマン物理学III, 前野昌弘電磁気学II講義録を主に参照, 改編させて頂いた。
ゲージ変換 都合の良いベクトル\(~\Vec A~\)を選ぶ
(2)式のベクトル\(~\Vec A~\)は何を意味するのだろうか?どうやって求めるのであろうか?こういうときは温故知新である。
スカラーポテンシャルを改めて見直してみよう。スカラーポテンシャル\(~\phi~\)では, 定数を加えた
\[\phi'=\phi+C \]
も同じ電場\(~\Vec E~\)を与えた。つまり\(~\phi~\)と\(~\phi'~\)は同じ物理量である。
\(C~\)は, 例えば無限遠でゼロのように, 都合の良いように決めた。おかげで見通しも良く, 計算も随分と容易になった。
ベクトルポテンシャルも便利な方が良い。異なるベクトルポテンシャル\(~\Vec A'~\)が同じ\(~\Vec B~\)を与えるのは
\[\Vec B=\nabla\x \Vec A=\nabla\x \Vec A'\]
\[\nabla\x \Vec A'-\nabla\x \Vec A=\nabla\x (\Vec A'-\Vec A)=0\]
のときである。あるベクトルの\(~rot~\)が 0 のとき, それは, あるスカラー場\(~\varphi~\)の\(~gradient~\)でなければならない。よって
\[\Vec A'=\Vec A+\nabla\varphi \]
は全ての\(~\varphi~\)に対して, 同様に正しいベクトルポテンシャル, 同じ\(~\Vec B~\)を与える。
更に\(~\Vec A~\)の自由度を減らしておくのが便利である。いくつか方法はあるが, 静磁場では
\[\nabla\cdot \Vec A=0\]
とすると都合が良い。理由はすぐにわかる。この条件を
クーロンゲージと呼ぶ。
自由度を減らす別の方法,
ローレンスゲージ(デンマークの\(~L.V.Lorenz\)。ローレンツ変換はオランダの\(~H.A.Lorenz\))は別の記事で説明する。
方程式が同じならば解も同じ ファインマン物理に度々登場するフレーズです。
(2)式の\(~\Vec B=\nabla\x \Vec A~\)は何かを推測した訳ではなく, 式変形だけで得た。物理的にはどのような意味があるのであろうか?
エネルギー保存則\(\displaystyle\int_C \Vec E\cdot d\bm{s}=0~\)が\(~rot\Vec E=0~\)を導き, \(~rot\Vec E=0~\)は電場を\(~\Vec E=-\nabla\phi~\)と表現することを可能にした。
\(\Vec E~\)を直接求めるより, \(~\phi~\)を微分した方がはるかに容易であることも知った。
\(~rot\Vec B\neq0~\)だから, 磁場\(~\Vec B~\)は何かの\(~gradient~\)としては表せない。静磁場\(~\Vec B~\)の基礎方程式は
\[\nabla\cdot\Vec B=0 \qquad\;\;\nabla\x \Vec B=\mu_0\bm{j}\]
である。\(~rot\Vec B\neq0~\)だが\(~div\Vec B=0~\)だから
\[\Vec B=\nabla\x \Vec A\]
は成り立つ。ベクトル場\(~\Vec A~\)をベクトルポテンシャルと呼ぶ。\(\Vec A~\)にスカラーポテンシャル\(~\phi~\)と同様の役割は期待できるだろうか?
注意:\(div\,rot\Vec A=0~\)について
適当なベクトル場を\(~\Vec A~\)とする。\(\nabla~\)はその定義式から明らかなようにベクトルである。\(\nabla\x \Vec A~\)は\(~\nabla~\)と\(~\Vec A~\)の両方に垂直なベクトルだから, \(\nabla~\)ベクトルと\(\nabla\x \Vec A~\)ベクトルの内積は 0。すなわち\(~\nabla\cdot\nabla\x \Vec A=0~\)である。
さて, 静電場では
\[\nabla^2\phi=-\frac{\rho}{\varepsilon_0}\tag{3} \]
が電位\(~\phi~\)の解を与える。
アンペールの法則\(~\nabla\x \Vec B=\mu_0 \bm{j}~\)を\(~\Vec B=\nabla\x \Vec A~\), および公式\(~\nabla\x (\nabla\x \Vec A)=\nabla(\nabla\cdot\Vec A)-\nabla^2 \Vec A~\)を用いて書き換えると
\[\begin{align}
\nabla\x \Vec B&=\nabla\x (\nabla\x \Vec A)=\nabla(\nabla\cdot\Vec A)-\nabla^2 \Vec
A \\
&=-\nabla^2 \Vec A\quad(\gets\nabla\cdot\Vec A=0) \\
&=\mu_0 \bm{j} \\
\nabla^2 \Vec A&=-\mu_0\bm{j}
\end{align}\]
が得られる。ここでクーロンゲージ, \(\nabla\cdot\Vec A=0~\)を用いた。
成分でみると
\[\nabla^2 A_x=-\mu_0 j_x \tag{4} \]
である (\(y,z~\)成分も同じ)。(3)式で\(~\phi\to A_x,\;\rho/\varepsilon_0\to \mu_0 j_x~\)とすれば数学的には同じだから, \(A_x~\)が求められるはずである。
あとは\(~\Vec A~\)を微分, すなわち\(~\nabla\x \Vec A~\)を実行して\(~\Vec B~\)を求めれば良い。
つまり定常電流の作る磁場は, ベクトルポテンシャルを微分して得られる。静電場と同じ方法で求められるわけである。
今のところベクトルポテンシャルの物理的な意味は不明だが, スカラーポテンシャルのように, 便利な方法として使ってみよう。
ベクトルポテンシャルの例
電流の作るベクトルポテンシャル
改めて書くと, \(\Vec A~\)は
\[\nabla\x \Vec A=\Vec B,\quad \nabla\cdot\Vec A=0\]
である。今一様な磁場\(~\Vec B_0~\)を考え, \(z~\)軸を磁場の方向に取ると, \(~\Vec B_0~\)の成分は\(~z~\)軸のみで,
\[\begin{align}
B_x&=\dd{A_z}{y}-\dd{A_y}{z}=0 \\
B_y&=\dd{A_x}{z}-\dd{A_z}{x}=0 \\
B_z&=\dd{A_y}{x}-\dd{A_x}{y}=B_0
\end{align}\]
可能な解は
\[A_y=xB_0,\;A_x=0,\;A_z=0\]
であり,
\[A_z=-yB_0,\;A_y=0,\;A_z=0\]
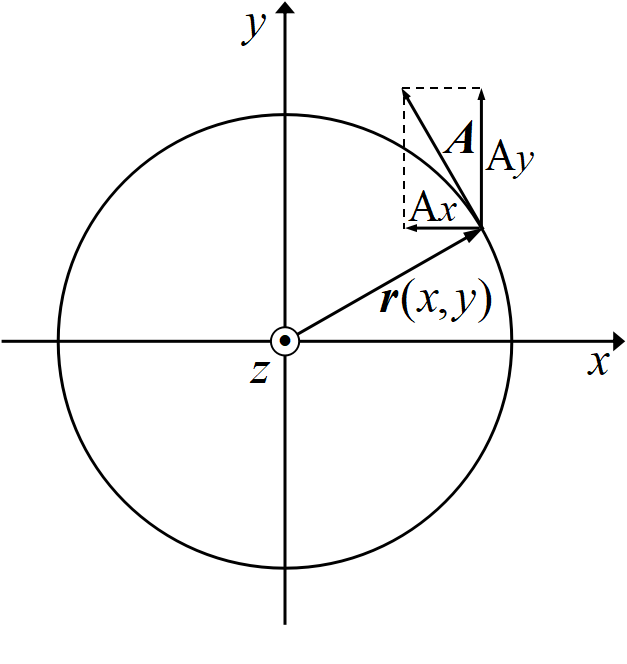
である。またその他の多くの解が存在するのは明らかだろう。上記2つの線形和
\[A_x=-\frac{1}{2}yB_0,\;A_y=\frac{1}{2}xB_0,\;A_z=0\]
も解である。3番目の線形和の解は, \(x~\)成分に\(~-y~\), \(y~\)成分に\(~x~\)を持つ
純粋回転場である。
ベクトルポテンシャル\(~\Vec A~\)は, \(z~\)軸, すなわち磁場\(~\Vec B_0~\)の周りを回っている。例えば\(~\Vec B_0~\)をソレノイド内の軸方向の場とすると, ベクトルポテンシャルはソレノイドの電流と同じ向き(電流と平行)に回る。
無限に長い直線電流の作る磁場
既に
ビオ・サバールの法則で求めたが, \(z~\)軸方向へ流れる直線電流の作る磁場に適用してみよう。
事前準備として
無限に長い帯電した細い円筒の外部の静電位を求める。主旨と異なるが, 円筒外部の静電位は, 電場\(~\to~\)電位の順が簡単である。
円筒外部の電場\(~E~\)は, 電荷の線密度を\(~\lambda~\), 円筒の中心からの距離を\(~r~\)とするとガウスの法則により,
\[E\cdot 2\pi r =\frac{\lambda}{\varepsilon_0} \]
円筒から距離\(~r~\)だけ離れた点の電位は
\[\begin{align}
\phi(r)&=-\int_{r_0}^{r}Edr \\
&=V_0-\frac{\lambda}{2\pi\varepsilon_0}ln\,r \\
&=-\frac{\lambda}{2\pi\varepsilon_0}ln\,r \tag{5}
\end{align}\]
無限長の直線上に電荷があるから無限遠の電位をゼロにできない。
どこかに基準を設ける場合は, 便宜上\(~V_0=0~\)として捨てる。あるいは\(~r=1~\)としても良い。
円筒の半径を\(~a~\), 電荷密度を\(~\rho~\)とすれば, 単位長さあたりの電荷は\(~\lambda=\pi a^2\rho\) だから
\[\begin{align}
\phi(r)&=-\frac{\lambda}{2\pi\varepsilon_0}ln\,r \\
&=-\frac{\pi a^2 \rho}{2\pi\varepsilon_0}ln\,r
\end{align}\]
ここで, \(\phi\to A_z,\;\rho/\varepsilon_0\to \mu_0 j_z~\)とすれば
\[A_z=-\frac{\pi a^2 \mu_0 j_z}{2\pi}ln\,r \]
が求められる。\(\pi a^2 j_z=I~\)であるから,
\[A_z=-\frac{\mu_0 I}{2\pi}ln\,r \tag{6} \]
と求まる。右辺の先頭の-(マイナス)は, \(A_z~\)が\(~z~\)軸の負の方向を向いているということでは無く, 導体からの距離\(~r~\)が大きくなるほど小さくなることを示している。
(5)式の静電位を求める過程で\(~V_0~\)を捨ててしまったことによる。
ベクトルポテンシャルは
電流と同じ向きで, 電流から遠ざかるほど小さくなる。
また, \(\Vec A~\)の大きさの差によって回転(渦)が生じている。
磁場\(~\Vec B~\)は\(~\Vec A~\)を微分して求められる。
\[\begin{align}
\Vec B=\nabla\x \Vec A=
\begin{pmatrix}
\dd{}{x}\\
\dd{}{y}\\
\dd{}{z}
\end{pmatrix}
\x
\begin{pmatrix}
A_x \\
A_y \\
A_z
\end{pmatrix}
=
\begin{pmatrix}
\dd{}{x}\\
\dd{}{y}\\
\dd{}{z}
\end{pmatrix}
\x
\begin{pmatrix}
0 \\
0 \\
A_z
\end{pmatrix}
=
\begin{pmatrix}
\dd{}{y}A_z \\
-\dd{}{x}A_z \\
0
\end{pmatrix}
\end{align}\]
だから, \(\sqrt{x^2+y^2}=r~\)として
\[\begin{align}
B_x&=-\frac{\mu_0 I}{2\pi}\dd{}{y}lnr=-\frac{\mu_0 I}{2\pi}\frac{y}{r^2}\\
B_y&=\frac{\mu_0 I}{2\pi}\dd{}{x}lnr=\frac{\mu_0 I}{2\pi}\frac{x}{r^2}\\
B_z&=0
\end{align}\]
が得られる。\(\Vec B~\)は導線を取り巻き, 大きさは
\[\begin{align}
B&=\sqrt{B_x^2+B_y^2} \\
&=\sqrt{\left(\frac{\mu_0 I}{2\pi}\right)^2 \left(\frac{x^2}{r^4}+\frac{y^2}{r^4}
\right)} \\
&=\sqrt{\left(\frac{\mu_0 I}{2\pi}\right)^2 \frac{1}{r^2}} \\
&=\frac{\mu_0 I}{2\pi r}
\end{align}\]
と以前と同じ結果が得られる。
極性ベクトルと軸性ベクトル \(~\Vec B~\)と\(~\Vec A~\)はどちらが実在か?
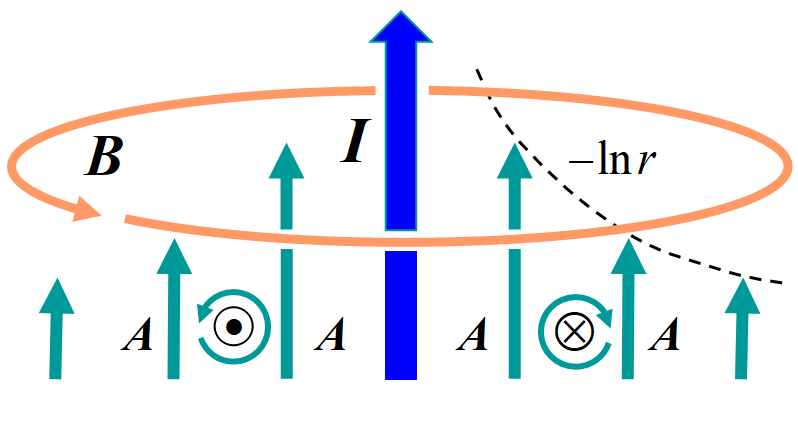
さてここで, 今まで度々出てきた, 直線電流の周りの磁場を考えよう。
ループ状の磁場には図のようなベクトルポテンシャルの渦がまとわりついて回っている。電流は磁場の中央を下から上へと流れている。
ところでベクトルには
極性ベクトルと軸性ベクトルがあった。
前者は物理的実体のあるベクトル, 後者は実体の無い計算の便宜のためのベクトルである。
電流に平行にベクトルポテンシャル\(~\Vec A~\)が発生し, そのベクトルが渦を発生させている。その渦の回転軸の向きを形式的に定めたのが磁場\(\Vec B~\)である。
右手系を左手系にすれば, 磁場の向きは逆向きになる。ただし\(~rot\Vec A~\)の回転の向きは変わらない。
こうしてみると, ベクトルポテンシャル\(~\Vec A~\)こそが実体で, \(\Vec B~\)は数学的便宜のための
偽ベクトルと言うことになる。
角運動量の場合は実体のあるのは, 原点から物体までの位置\(~\bm{r}~\)および物体の運動量\(~m\bm{\upsilon}~\)である。
角運動量ベクトルの向きは, 空間反転(右手系\(~\rightleftarrows~\)左手系)すると変わってしまい, そのために
偽ベクトルと呼ばれるが, 回転の向き\(~m\bm{\upsilon}~\)は変わらない。その意味では
軸性ベクトルと呼ぶ方が良いかもしれない。
微小電流ループの作る磁場・磁気モーメント
微小な電流ループが作り出す磁場は, ビオ・サバールの法則から直接計算, あるいは一旦
\[\Vec A(\bm{r})=\nabla\x \frac{\mu_0 I}{4\pi}\int_C d\bm{s}\frac{1}{r}\tag{7}\]
を計算して, その結果を\(~\Vec B=\nabla\x \Vec A(\bm{r})~\)で微分して求める。
(7)式を求める目的は, 計算を簡易にするためであるとの説明が多く, 殆どの教科書では(7)式で計算しているようである。
筆者が実際に計算して見ると, この記事の程度ではビオ・サバールの式から直接計算するのと大差ない感じがした。
ここではクーロンゲージを使って求めて見よう。
電流ループの話に入る前に,
電気双極子モーメントの電位について, ざっとおさらいする。
2つの電荷\(~-q,\,+q~\)がそれぞれ\(~P~\)点に作るポテンシャルを重ね合わせ, 適当な近似計算をすればよい。
\(P~\)の位置ベクトルを\(~\bm{r}~\)とする。\(P~\)のポテンシャルは
\[\begin{align}
U(\bm{r})
&=\frac{1}{4\pi\varepsilon_0}\frac{q}{r_1}-\frac{1}{4\pi\varepsilon_0}\frac{q}{r_2}\\ &=\frac{q}{4\pi\varepsilon_0}\left(\frac{1}{\sqrt{r^2+\left(\frac{s}{2}\right)^2-
rs\cos\theta}}-\frac{1}{\sqrt{r^2+\left(\frac{s}{2}\right)^2+rs\cos\theta}}\right)\\
&=\frac{\bm{p}\cdot\bm{r}}{4\pi\varepsilon_0 r^3}\tag{8}
\end{align}\]
\(\bm{p}~\)は電気双極子モーメントで, \(-q~\)から\(~+q~\)へ向かうベクトルで, 大きさは2つの電荷\(~-q,\,q~\)の距離を\(~s~\)として
\[\bm{p}=q\bm{s}\]
である。
クーロンゲージでは, \(\phi\to A_i,\;\rho/\varepsilon_0\to \mu_0 j_i~\)とすれば, スカラーポテンシャル\(~\phi~\)からベクトルポテンシャル\(~A_i~\)が得られ, \(~A_i~\)を微分して静磁場\(~\Vec B~\)が得られるのであった。
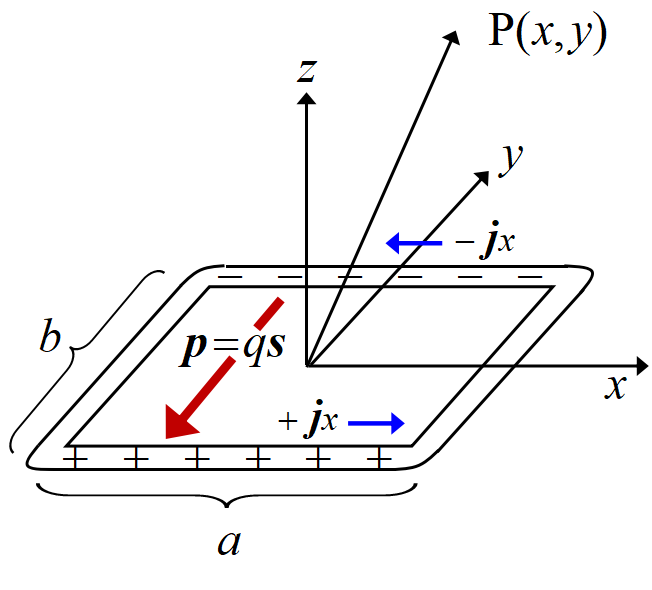
電流ループの電荷の線密度を\(~\lambda~\), 体積密度を\(~\rho~\), 導線の半径を\(d~\)とすると, \(\lambda=\pi d^2 \rho~\)であり, 図の\(~x~\)軸に平行な部分の電荷は\(~q=\lambda a~\)である。
クーロンゲージでは\(~\rho/\varepsilon_0\to \mu_0 j_i~\)という対応を取る。
\(\lambda a=\pi d^2 \rho a=\pi d^2 \varepsilon_0 \mu_0 j_i a ~\)より, 電荷\(~q=\lambda a ~\)の符号は, \(-j_x~\)部分が\(~-q~\), \(+j_x~\)部分が\(~+q~\)の電気双極子モーメントと考えれば良い。
\[\bm{p}=\lambda a\bm{b} \tag{9} \]
である。
双極子モーメントが\(~y~\)軸の負の方向に向くから, (8)式の\(~\bm{p}~\)と\(~\bm{r}~\)の間の角の\(~cos~\)は\(~-y/r~\)である。すると(8)式は
\[
\phi=\frac{\bm{p}\cdot\bm{r}}{4\pi\varepsilon_0 r^3}=-\frac{1}{4\pi\varepsilon_0}\frac{\lambda ab}{r^2}\frac{y}{r}\\
\]
ここで(クーロンゲージでの)対応\(~\lambda ab=\pi d^2 \rho ab \to\varepsilon_0 \mu_0\pi d^2 j_i ab ~\)より
\[A_x=-\frac{1}{4\pi\varepsilon_0} \frac{\varepsilon_0\mu_0(\pi d^2 j_i) ab}{r^2}\frac{y}{r} =-\frac{\mu_0 Iab}{4\pi} \frac{y}{r^3} \]
を得る。同様にして
\[A_y=-\frac{\mu_0 Iab}{4\pi} \frac{x}{r^3} \]を得る。磁場\(~\Vec B~\)は\(~\Vec A~\)を微分して
\[\begin{align}
\Vec B=\nabla\x \Vec A=
\begin{pmatrix}
\dd{}{x}\\
\dd{}{y}\\
\dd{}{z}
\end{pmatrix}
\x
\begin{pmatrix}
A_x \\
A_y \\
A_z
\end{pmatrix}
=
\begin{pmatrix}
\dd{}{x}\\
\dd{}{y}\\
\dd{}{z}
\end{pmatrix}
\x
\begin{pmatrix}
A_x \\
A_y \\
0
\end{pmatrix}
=
\begin{pmatrix}
-\dd{}{z}A_y \\
\dd{}{z}A_x \\
\dd{}{x}A_y-\dd{}{y}A_x
\end{pmatrix}
\end{align}\]
より
\[B_x=-\dd{}{z}\frac{\mu_0 Iab}{4\pi}\frac{x}{r^3}=-\frac{\mu_0 Iab}{4\pi}\frac{3xz}{r^5} \]
\[B_y=\dd{}{z}\frac{\mu_0 Iab}{4\pi}\frac{y}{r^3}=\frac{\mu_0 Iab}{4\pi}\frac{3yz}{r^5} \]
\[B_z=\frac{\mu_0 Iab}{4\pi} \left(\dd{}{x}\frac{y}{r^3}-\dd{}{y}\left(-\frac{y}{r^3} \right) \right)=\frac{\mu_0 Iab}{4\pi}\left(\frac{1}{r^3}-\frac{3z^2}{r^5} \right)\]
を得る。
磁気モーメント
(9)式は\(~x~\)軸に平行な電流密度\(~+j_x,\,-j_x~\)を電荷と見立てて電気双極子の形に書いたものである。
\(~y~\)軸に平行な電流密度\(~+j_y,\,-j_y~\)を用いれば
\[\bm{p}=Ib\bm{a} \tag{10} \]
となる。大きさはいずれも\(~I\x ab~\)すなわち, 電流×面積となっている。ループ面の単位法線ベクトルを\(\bm{n}~\)とすると, (9), (10)式はまとめて
\[\bm{m}=Iab\bm{n} \tag{11}\]
と書け, ベクトルポテンシャルを
\[\Vec A=\frac{\mu_0}{4\pi}\frac{\bm{m}\x \bm{r}}{r^3} \tag{12} \]
と, (8)式と対称性の良い形に書ける。
(11)式を
磁気モーメントと呼ぶ。磁気双極子モーメントと呼ぶこともあるが, 磁気には
極となる磁荷が存在しないので, 歴史的意味合いだけだろう。
ベクトルポテンシャルの物理的な意味 単位電流当たりの位置エネルギー
ベクトルポテンシャルの例をいくつか見てきたが, スカラーポテンシャルほどは便利ではない。数学のお遊びだけならば少々残念である。
磁場\(~\Vec B~\)の中に, 電流\(~\Vec I~\)と同じ向きに電流\(~\Vec i~\)を置く。この電流\(~\Vec i~\)が, 長さ\(~l~\)当たりに受ける力\(~\Vec F_m~\)は, 電流\(~I~\)に引かれる引力なので
\[\Vec F_m=-il\Vec B=-\frac{\mu_0Iil}{2\pi r} \]
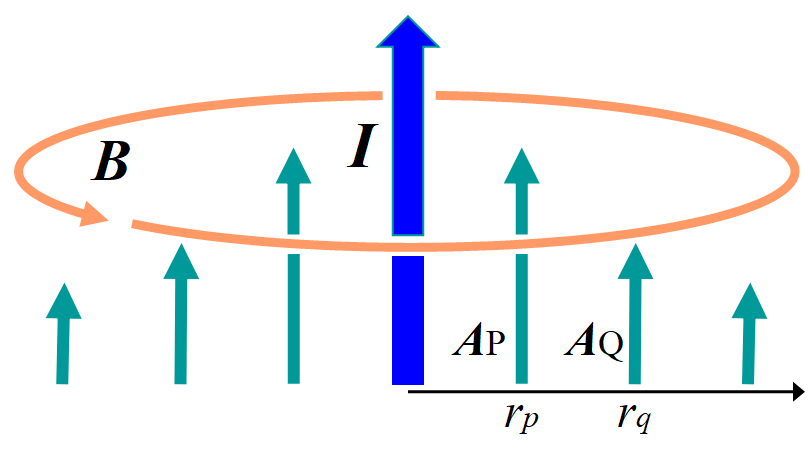
である。この電流棒を磁場\(~\Vec B~\)の中を\(~P~\)から\(~Q~\)へ運ぶには, \(~\displaystyle\Vec A(r)=\frac{\mu_0 I}{4\pi}\int \frac{ds}{r}\)を用いて,
\[\begin{align}
U_m&=\int_{P}^{Q}\Vec F_m\cdot d\bm{r} \\
&=-\frac{\mu_0 I il}{2\pi}\int_{P}^{Q}\frac{dr}{r} \\
&=-2il\x \frac{\mu_0 I}{4\pi}\int_{P}^{Q}\frac{dr}{r} \\
&=-2il(A_Q-A_P)
\end{align} \]
のエネルギーが必要となる。またこれは電界中の電荷の運搬と同様, 経路によらない。
なお上式右辺の\(~2~\)は\(~1~\)として, \(U_m=-il(A_Q-A_P)\)が正しい。
静電場のエネルギーを計算した時と同様, 電流\(~\Vec i~\)自身もベクトルポテンシャルを作り, エネルギーを2倍に数えてしまうからである。電流の向きと磁場の向きが異なるときは内積を取れば良い。
ベクトルポテンシャルは単位長さ当たりの電流\(~\Vec i\x 1\,[A\cdot m]~\)に対して,
\[-\bm{i}\cdot \Vec A\]
のエネルギーを与える。
ベクトルポテンシャルは, 電界中の電荷の運搬と, 磁場中の電流の運搬との違いはあるが, 保存力を意味するポテンシャルである。