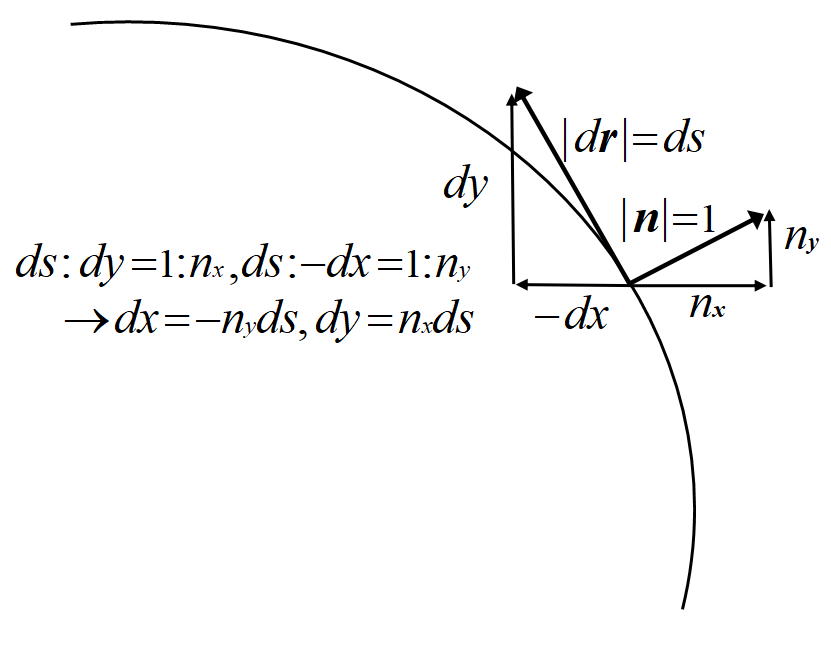ベクトル場の発散と回転
ベクトル場
ベクトル場とは, 空間のすべての点において, その点\((x,y,z)\)を始点とするベクトルが定義されているベクトルの集合。
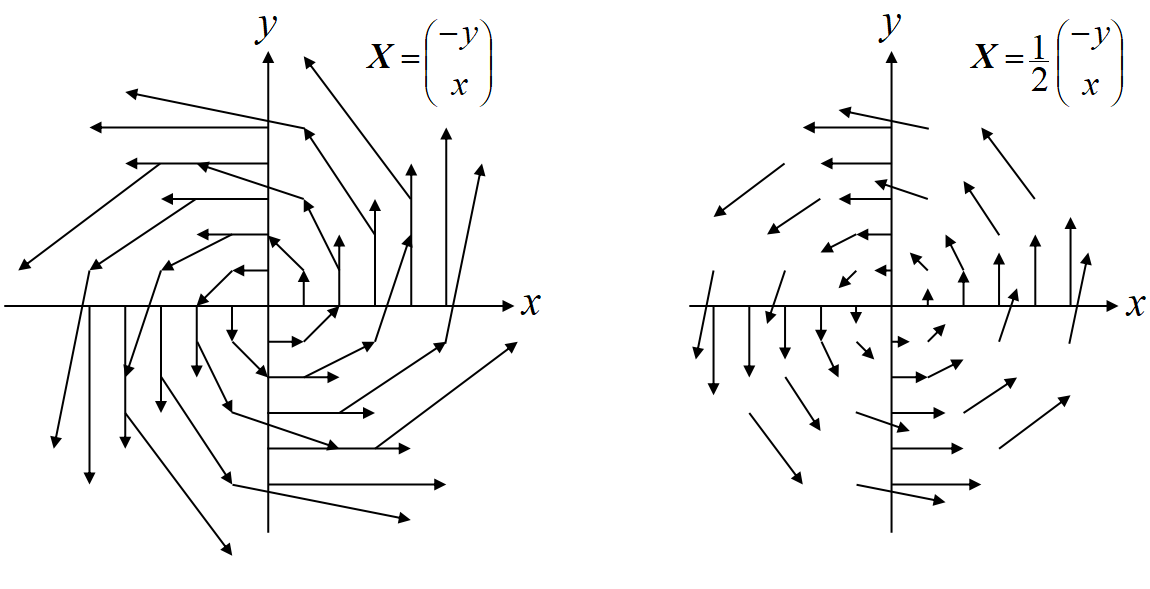
回転ベクトル場として良く引用される\(\Vec X_{x,y,0}=(-y,x,0)\)は, \(\Vec X\)の添え字が始点で, 成分が\((-y,x,0)\)となるようなベクトルである。
\(\Vec X_{1,0,0}=(0,1,0),\ \Vec X_{1,1,0}=(-1,1,0),\ \Vec X_{2,1,0}=(-1,2,0)\)等である。これを図示したものが上の左図であるが, 回転しながら湧き出しているようにも見える。筆者にはそうとしか見えなかった。
\(\Vec X_{x,y,0}=\frac{1}{2}(-y,x,0)\)としたものが右図である。回転ベクトル場であることが分かるだろう。
ベクトル場の発散 先ずは分かり易い発散の方から
スカラー関数\(~\phi(x,y,z)\)の勾配を表すベクトルとして
\[\nabla \phi \equiv \left(\dd{\phi}{x}, \dd{\phi}{y}, \dd{\phi}{z}\right) \]
というものが定義できた。この\(\nabla \phi \)を関数\(~\phi(x,y,z)\)の勾配, またはグラディエントと呼ぶ。ここで使っている記号\(\nabla \)を
ナブラと呼ぶ。
このナブラだけをグラーディエントから切り離して, ベクトル微分演算子,
\[\nabla\equiv \left(\dd{}{x}, \dd{}{y}, \dd{}{z} \right) \tag{1} \]
を導入する。
さてここで, このナブラとベクトル\(\Vec A = (A_x,A_y,A_z)\)との内積
\[div\Vec A= \nabla \cdot \Vec A= \dd{A_x}{x}+\dd{A_y}{y}+\dd{A_z}{x} \tag{2} \]
をベクトル場\(\Vec A = (A_x,A_y,A_z)\)の
発散または
ダイバージェンス
\((divergence)\)と呼ぶ。
内積を用いているが, ベクトルと実数を対応させるとか, 射影演算子としての内積とか, そのような大それた意味は無い。
(2)式の右辺の量の計算に便利なだけであり, 記号としても扱いやすい。
(2)式の右辺を見てみよう。例えば第1項\(~\partial A_x/\partial x\)が正だとすると, \(~A_x\)は徐々に増加する。\(~A_y\), \(~A_z\)も同様とすると, ベクトル\(~\Vec A\)は徐々に大きくなる。ベクトル\(~\Vec A\)が水流とすると, 徐々に流量が増えてゆくようなイメージである。本当にそうなっているか?確かめてみよう。
一般のベクトル場だとイメージが湧かないので, 水流(非圧縮量体)で考えてみよう。
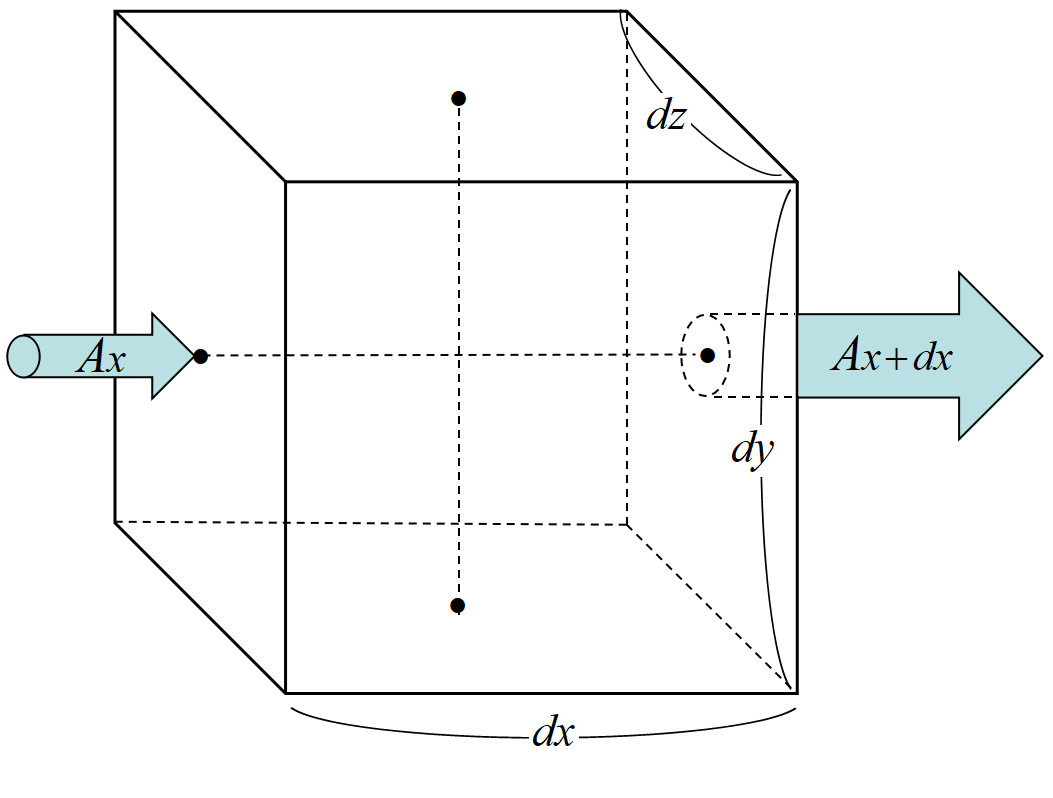
水流中の微小体積部分\(~dxdydz~\)を考える。\(~x~\)の地点で単位面積辺り\(~A_x\)の水流が\(~x~\)方向に流れているとする。\(~dx~\)だけ離れた地点での流量は
\[A_x+\dd{A_x}{x}dx \]
である。\(~x~\)に垂直な面の面積は\(~dydz~\)であるから, 流量の増加は
\[\left(A_x+\dd{A_x}{x}dx-A_x\right)dydz= \dd{A_x}{x}dxdydz \tag{3}\]
となる。一方(2)式の両辺に微小体積\(~dv= dxdydz~\)を掛けると
\[\begin{align}
\nabla \cdot \Vec A dv
&= \left(\dd{A_x}{x}+\dd{A_y}{y}+\dd{A_z}{z}\right)dxdydz \\
&= \dd{A_x}{x}dxdydz+\dd{A_y}{y}dxdydz+\dd{A_z}{x}dxdydz \tag{4}\\
\end{align}\]
(3)式と(4)式右辺第1項は等しい。
つまり(4)式右辺第1項は微小な直方体の\(yz~\)面から\(~x~\)方向に向かって入った水流が, この直方体の中を通り抜ける間の増加量を表している。
\(~y,z~\)方向も同様であるから, 結局(4)式の右辺は全ての方向の増加量の和になっており, 微小体積\(~dv= dxdydz~\)から新たに「湧きだした水量」を表していることになる。
\(~div \Vec A~\)をベクトル場\(~\Vec A~\)の
発散, あるいは
湧きだしとしたのは名訳であろう。
ベクトル場の回転 数式だけだと分からない
ベクトル場\(~\Vec A= (A_x, A_y, A_z)\)に対して, 次のように定義した量を回転と呼ぶ。
\[
\begin{align}
rot\Vec A &= \nabla \x \Vec A \\
&=
\begin{pmatrix}
\dd{}{x} \\
\dd{}{y} \\
\dd{}{z} \\
\end{pmatrix}
\x
\begin{pmatrix}
A_x \\
A_y \\
A_z \\
\end{pmatrix}\\
&=
\begin{pmatrix}
\dd{A_z}{y}-\dd{A_y}{z} \\
\dd{A_x}{z}-\dd{A_z}{x} \\
\dd{A_y}{x}-\dd{A_x}{y} \tag{5}
\end{pmatrix}\\
\end{align}
\]
これで終わりであるが, 式からだけではイメージが全く湧かない。\(~Z~\)軸方向の成分,
\[\dd{A_y}{x}-\dd{A_x}{y} \tag{6}\]
について考えてみよう。
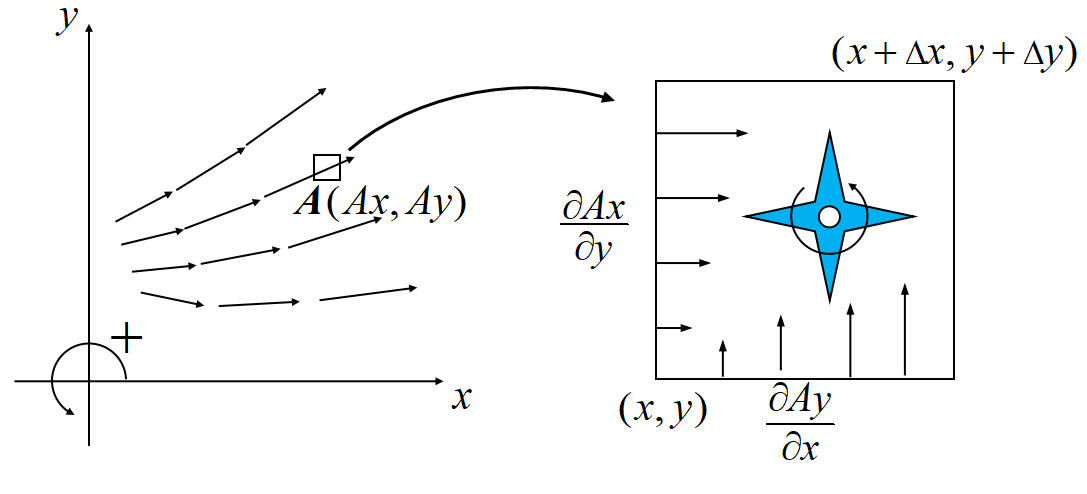
水車が水流\(~\Vec A~\)によって回転しているとする。反時計回りを正の回転とする。
水流の\(~y~\)方向成分\(~A_y\)については, 水車の左側より右側が大きいとき, すなわち
\(~\partial A_y/\partial x~\)が正の時, 水車は正方向に回転する。
\(~x~\)方向成分\(~A_x\)については, 水車を正回転させるのはマイナスがついて\(-\partial A_x/\partial y~\)となるのは理解できるであろう。
(5)式の\(~z~\)成分\(~\partial A_y/\partial x -\partial A_x/\partial y~\)は, \(xy~\)平面で水車を回転させる勢いを表している。\(~rot~\), 回転と呼ばれる所以である。
トルクを使えばもう少し定量的な議論が出来るが, この位で良いであろう。
ガウスの発散定理とストークスの回転定理
ガウスの発散定理 直感的には分かり易いが証明は相当厄介。
ガウスの発散定理は, 体積積分と面積分を変換する定理である。
\[\int_V div \Vec A dv= \int_S \Vec A \cdot \bm{n} dS \]
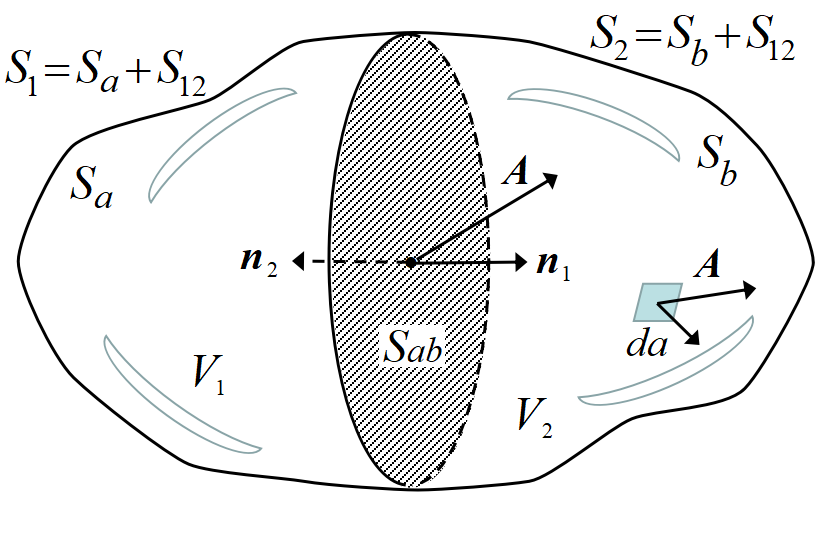
任意の閉曲面\(~S~\)で囲まれた体積を, 平面\(~S_{ab}~\)で区切り, \(~V_1\)と\(~V_2\)に分ける。
曲面\(~S_a\)と\(~S_{ab}\)で囲まれた部分\(~V_1~\)から出てゆくベクトル\(\Vec A~\)の流束は
\[\int_{S_a}\Vec A\cdot \bm{n}da + \int_{S_ab}\Vec A\cdot \bm{n_1}da \]
\(~V_2~\)から出てゆくベクトル\(\Vec A~\)の流束は
\[\int_{S_b}\Vec A\cdot \bm{n}da + \int_{S_ab}\Vec A\cdot \bm{n_2}da \]
ここで明らかに\(~\bm{n}_1=-\bm{n}_2\)だから, \(~S_1\)と\(~S_2\)を通る流束の和は
\[\int_{S_a}\Vec A\cdot \bm{n}da + \int_{S_b}\Vec A\cdot \bm{n}da \]
で, もとの面\(~S= S_1+S_2\)の流束になる。改めて書き直すと,
微小体積\(~V_1\)と\(~V_2\)から湧き出した流束の和は,\(~V_1, V_2\)を含む面\(~S= S_1+S_2\)を通る流束と等しい。これを全表面, 全体積に拡張したものが, ガウスの発散定理である。
ガウスの発散定理は「内部の湧き出しを全部集めたものは, 表面から出てゆく全流束と等しい」という, 感覚的に非常に分かり易いものである。筆者もきちんとした証明は知らずに過ごしてきたが, 何の不自由も感じなかった。
でも, まあ一度はやってみよう。3次元の証明は本当に厄介で紙面の無駄遣いになるので, 2次元版で示す。
改めてガウスの発散定理(2次元版)を書くと
\[\iint_S div\Vec A dS= \int_C \Vec A \cdot \bm{n}ds \]
である。\(\displaystyle div\Vec A = \dd{A_x}{x}+\dd{A_y}{y}\)が2次元版の発散で,
領域\(~S~\)の内部から外部への湧き出し, \(\displaystyle \iint_S div\Vec A ds\)は, 内部から外部への湧き出し量の総和となる。
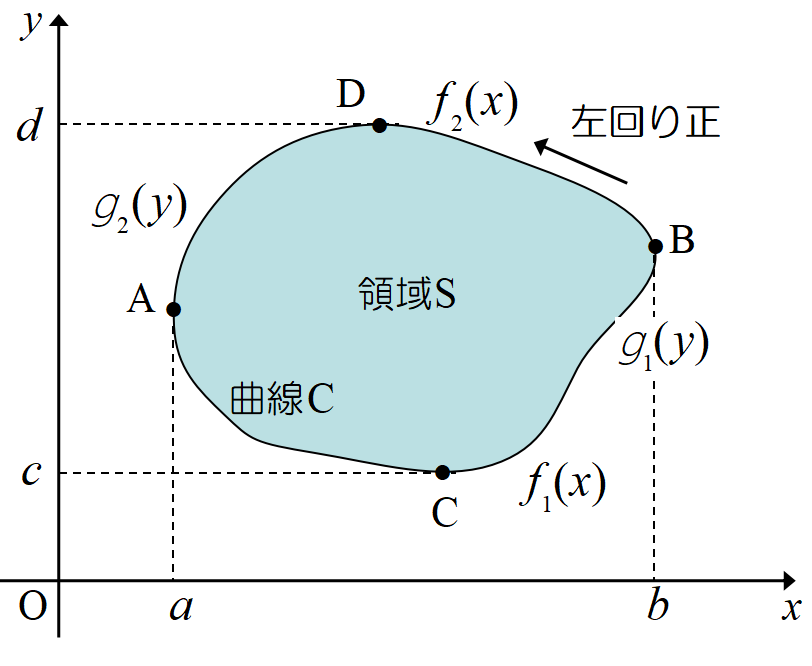
ここで\(~\Vec A= (A_x(x,y),A_y(x,y))\)とする。図の下側の曲線を\(~y= f_1 (x)\), 上側の曲線を\(~y= f_2 (x)\)とする。面積積分は,
\[\begin{align}
\iint_S div\Vec A dS &= \iint_S \left(\dd{A_x}{x}+\dd{A_y}{y} \right)dS \\
&= \iint_S \dd{A_x}{x}dS+ \iint_S \dd{A_y}{y}dS \tag{7} \\
\end{align}\]
かなり技巧的であるが, (7)式右辺の第2項を変形してゆく。
\[\begin{align}
\int_{a}^{b}\int_{f_1(x)}^{f_2(x)}\dd{A_y}{y}dydx
&= \int_{a}^{b}\{A_y(x,f_2(x))-A_y(x,f_1(x))\}dx \tag{8} \\
&= \int_{a}^{b}A_y(x,f_2(x))dx - \int_{a}^{b}A_y(x,f_1(x))dx \tag{9} \\
&=-\left(\int_{a}^{b}A_y(x,f_1(x))dx+\int_{b}^{a}A_y(x,f_2(x))dx
\right)\tag{10}\\
&=-\oint_C A_y(x,y)dx \tag{11} \\
\end{align}\]
を得る。
途中(8)式の左辺から右辺は, \(~\partial y~\)と\(~dy~\)を約分し, 残りは\(~\partial A_y~\)のみなので, \(~A_y~\)で積分して\(A_y(x,f_2(x))-A_y(x,f_1(x))\)。
(9)式第1項の積分順序を\(~b \to a~\)にしてまとめた式が(10)式。
(10)式右辺第1項は\(~f_1(x)\), 第2項は\(~f_2(x)\)となっている。
全体で\(~A \to B \to A~\)と回る, ベクトル\(~\Vec A~\)の\(~y~\)成分\(~A_y(x,y)~\)の周回積分となっている。周回を強調するために\(~\oint~\)を使った。
同様にして, 曲線\(~C~\)を左右に分け, 左側を\(~g_1(y)\), 右側を\(~g_2(y)\)とし, \(C \to D \to C~\)の周回積分を行う。(7)式の第1項は
\[
\int_{c}^{d}\int_{g_1(y)}^{g_2(y)}\dd{A_x}{x}dxdy =\oint_C A_x(x,y)dy \tag{11}
\]
となる。結局(7)式は
\[\begin{align}
\iint_S div\Vec A dS &= \iint_S \left(\dd{A_x}{x}+\dd{A_y}{y} \right)dS \\
&= \oint_C A_x(x,y)dy -\oint_C A_y(x,y)dx \\
&= \oint_C \{A_x(x,y)dy -A_y(x,y)dx\} \tag{12} \\
\end{align}\]
となる。接線ベクトル\(~d\bm{r}(dx,dy)~\)と単位法線ベクトル\(~\bm{n}(n_x,n_y)~\)の関係は
\(dx=-n_yds, dy=n_xds~\)を(12)式に代入すると
\[\begin{align}
&= \oint_C \{A_x(x,y)dy -A_y(x,y)dx\} \tag{12} \\
&= \oint_C \{A_x(x,y)n_x+A_y(x,y)n_y\}ds \\
&= \oint_C \Vec A\cdot\bm{n}ds \\
\end{align}\]
となる。これはベクトル\(~\Vec A~\)と単位法線ベクトル\(~\bm{n}~\)の内積の, 曲線\(~C~\)に沿った線積分である。
\[\iint_S div\Vec A dS= \int_C \Vec A \cdot \bm{n}ds \]
が証明された。ふ~!
3次元版は立体を平面で切断し, \(~xy~\)平面に射影し\(~x, y~\)で積分, \(~yz~\)平面に射影し\(~y, z~\)で積分‥‥。更に技巧的で式もまともに追えない。
ストークスの回転定理 直感的に分かり難いが証明は意外と簡単。
ベクトル場\(~\Vec A~\)の中の閉曲線に沿った線積分,
\[\int_C\Vec A\cdot d\bm{r} \]
を, ベクトル場\(~\Vec A~\)の\(~C~\)に沿った循環という。\(~d\bm{r}~\)は\(~C~\)の線素ベクトルである
ストークスの回転定理は, 閉曲線\(~C~\)に沿った循環(線積分)を面積分に変換する定理である。
\[\int_C \Vec A\cdot d\bm{r}= \int_S rot\Vec A \cdot d\Vec S \tag{13}\]
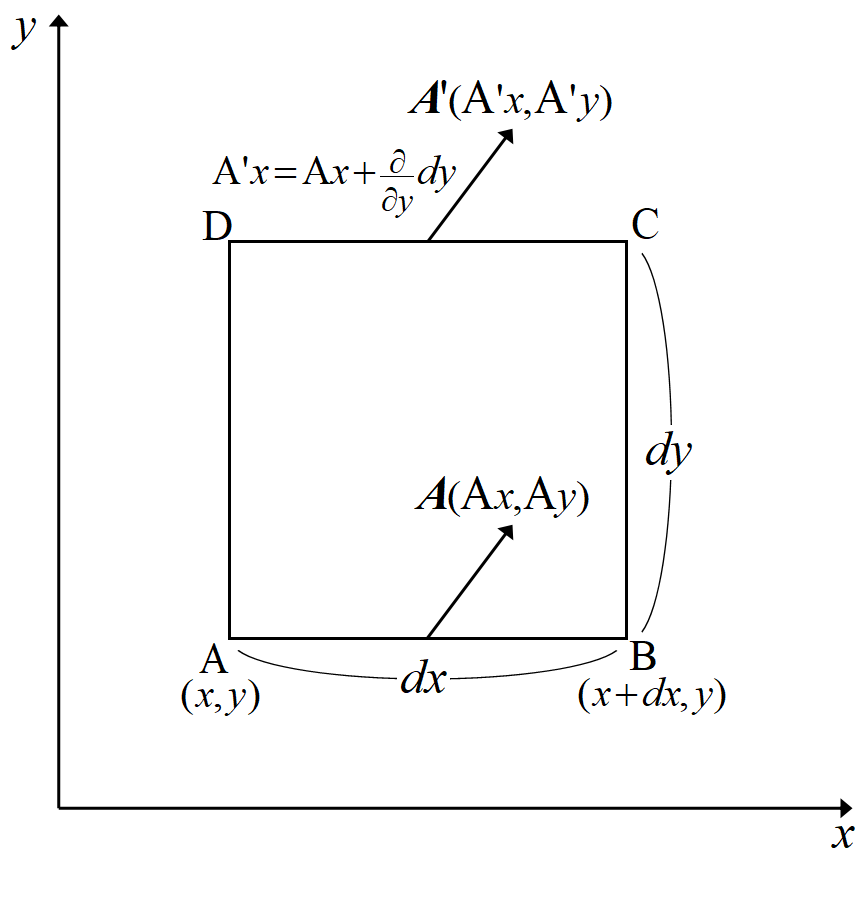
ベクトル\(~\Vec A~\)を図の\(~A \to B \to C \to D\)に沿って線積分する。
先ず\(~x~\)方向\(~A\to B, C \to D~\)を考えると, \(A_x dx-A'_x dx \)。\(A_x \)の変化率を考慮すると,
\[A'_x= A_x+\dd{A_x}{y}dy \]
だろうから,
\[A_x dx-A'_x dx =-\dd{A_x}{y}dxdy \]
となる。\(~y~\)方向\(~B\to C, D \to A~\)も同様にして,
\[A_y dy-A'_y dy = \dd{A_y}{x}dxdy \]
であるから, 四角形\(~ABCD~\)回りの循環(線積分)は,
\[\left(\dd{A_y}{x}- \dd{A_x}{y} \right)dxdy \]
となり, (7)式, すなわち\(~rot \Vec A~\)(の\(~z~\)成分)に微小面積\(~dxdy~\)を掛けたものと同じになる。
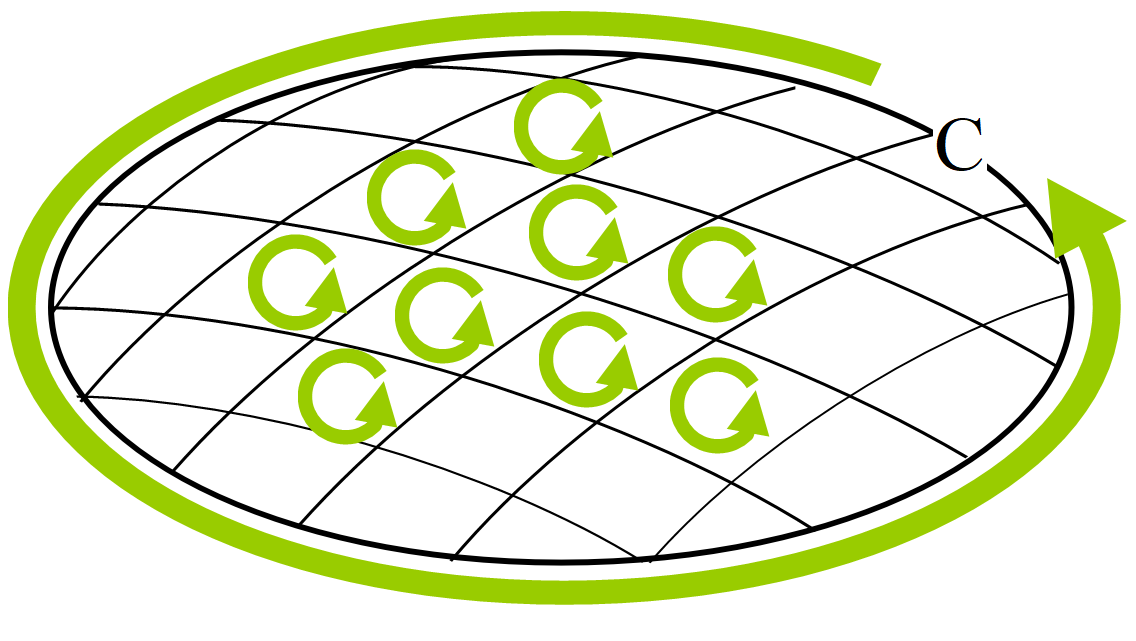
大きな面積では, 微小面積の隣り合った部分は打ち消し合うので, 結局1番外側の曲線に沿った循環のみが残る。
ヘルムホルツの定理 ベクトル解析の基本定理
「全てのベクトル場は純粋発散型と純粋回転型のベクトル場の和で表される」
正しくは, 任意のベクトル場\(\Vec A\)は, スカラーポテンシャル\(~\phi\), ベクトルポテンシャル
\(\Vec X\)を用いて,
\[\Vec A= \nabla \phi + \nabla \x \Vec X \]
と表されるものである。とても大切な定理であるが, 証明にはベクトル解析の他の定理も必要なので, 今は天下りに受け入れよう。
ベクトル場の2階微分 重要なのは2つ
\(\nabla\x (\nabla \phi)=0~\)と\(\nabla\cdot(\nabla\x \Vec A)=0\)
渦無し場の回転 \(\nabla\x (\nabla \phi)=0~\)
\[\begin{align}
\nabla \x \nabla \phi
&= \nabla \x \left(\dd{\phi}{x},\dd{\phi}{y},\dd{\phi}{z}\right) \\
&= \left(
\frac{\partial^2 \phi}{\partial z\partial y}-\frac{\partial^2 \phi}{\partial y \partial z},
\frac{\partial^2 \phi}{\partial x\partial z}-\frac{\partial^2 \phi}{\partial z \partial x},
\frac{\partial^2 \phi}{\partial y\partial x}-\frac{\partial^2 \phi}{\partial x \partial y}
\right) \\
&= (0,0,0)
\end{align}\]
とまあ, 簡単に結果が出てしまった。ゼロベクトルである。物理的にはどんな意味があるのだろう。
ストークスの回転定理(13)によれば, \(~rot \Vec A~\)が\(~0~\)であるようなベクトル場\(~\Vec A~\)の任意のループのまわりの循環は\(~0~\)である。
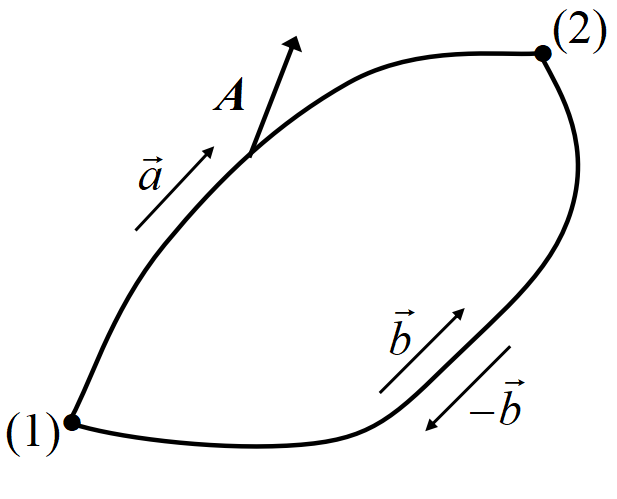
二つの点\((1)\)と\((2)\)とを閉曲線上にとると, 接線成分の\((1)\)から\((2)\)までの積分は二つの可能な道筋\((~\vec a, \vec b ~)\)のどちらをとっても同じである。
すなわち\(\displaystyle \int_{\vec a}\Vec A\cdot d\bm{s} + \int_{-\vec b}\Vec A\cdot d\bm{s}= 0~\)より
\(\displaystyle \int_{\vec a}\Vec A\cdot d\bm{s}= -\int_{-\vec b}\Vec A\cdot d\bm{s}= \int_{\vec b}\Vec A\cdot d\bm{s}\)。
従って\((1)\)から\((2)\)までの積分はこの2点の位置 (\(x,y,z\)) だけ, つまり場所の関数である。
このような関数を
スカラーポテンシャルと呼ぶのであった。
任意の点で\(~\nabla\x \Vec A=0~\)ならば, その\(\Vec A\)はスカラーポテンシャル関数\(~\phi~\)の勾配である。逆も成り立ち,
任意のスカラーポテンシャルの勾配の回転はゼロである。ということになる。
因みに, あるベクトル\(~\Vec B~\)が, \(\Vec B= \nabla\x \Vec A~\)と書けるとき, \(~\Vec A~\)を
ベクトルポテンシャル, スカラーポテンシャルとベクトルポテンシャルを合わせて
電磁ポテンシャルと呼ぶ。
回転場の発散 \(\nabla\cdot(\nabla\x \Vec A)=0\)
\[\begin{align}
\nabla\cdot(\nabla\x \Vec A)
&=div\left(\dd{A_x}{y}-\dd{A_y}{z},\dd{A_x}{z}-\dd{A_z}{x},\dd{A_y}{x}-\dd{A_x}{y} \right) \\
&=\dd{}{x}\left(\dd{A_x}{y}-\dd{A_y}{z}\right)
+\dd{}{y}\left(\dd{A_x}{z}-\dd{A_z}{x}\right)
+\dd{}{z}\left(\dd{A_y}{x}-\dd{A_x}{y}\right) \\
&=\frac{\partial^2 A_x}{\partial y \partial x}-\frac{\partial^2 A_y}{\partial z
\partial x}
+\frac{\partial^2 A_x}{\partial z \partial y}-\frac{\partial^2 A_x}{\partial x
\partial y}
+\frac{\partial^2 A_y}{\partial x \partial z}-\frac{\partial^2 A_x}{\partial y
\partial z} \\
&=0
\end{align}\]
今度はスカラーのゼロである。こちらはどんな意味があるのだろうか?
色々調べてみたが, 様々な見方があるようである。
ぐるぐる巻いている渦は, 循環はしているが, そこからの湧き出しは無い。当然のような気もする。
ただ, \(~rot\Vec A _z= \partial A_y/\partial x - \partial A_x/\partial y~\)は渦そのものではなく, 並行する流れの流速の差を表しているので, 何とも言えない。
その他の2階微分
\(div~\),\(~grad~\),\(~rot~\)の組合せなので沢山あるが, 実用的なものは限られている。
\[div\ grad=\nabla\cdot\nabla=\left(\dd{\ ^2}{x^2}+\dd{\ ^2}{y^2}+\dd{\ ^2}{z^2}\right)\]
はラプラシアンまたはラプラス演算子と呼ばれ, ポアソン方程式, ラプラス方程式で使うので覚えよう。
\(\nabla\cdot\nabla\)は\(~\nabla^2\)、または\(~\triangle~\)と書かれる場合が多い。
\[\triangle\equiv\nabla^2\equiv\nabla\cdot\nabla\]
また
\[rot\ rot\Vec A= grad\ div\Vec A -\Delta \tag{14}\]
は\(~Maxwell~\)方程式から, 電場, 磁場の波動方程式を導くとき用いられるが, 憶える必要は無い。
H22年度の\(~T~\)大学大学院物理博士課程の入試で波動方程式の導出が出題されたが, (14)式は問題文に書かれていた。