エネルギー保存の法則
エネルギー保存則という用語がいささか曖昧に使われている。ここでは以下の2つに分けて考える。
(1) 力学的エネルギー保存則
(2) 全てのエネルギーを含んだエネルギー保存則
(1)の定義は資料によって若干異なるが, 力学的エネルギー\(~=~\)運動エネルギー\(~+~\)位置エネルギー(ポテンシャル)\((Wikipedia)\)が標準的であり, 位置エネルギー\(~=~\)重力位置エネルギー\(~+~\)弾性力位置エネルギーとしているところもある(金沢工大)。
位置エネルギーは何かというと「保存力のする仕事」。「保存力」は何かと言うと「力学的エネルギーを保存する力」あるいは「2点間のエネルギーの差が途中の経路によらない力」との説明が多い。
で, 「保存力」とは一体何なんだ?そこで保存力から説明することにする。
保存力とは?
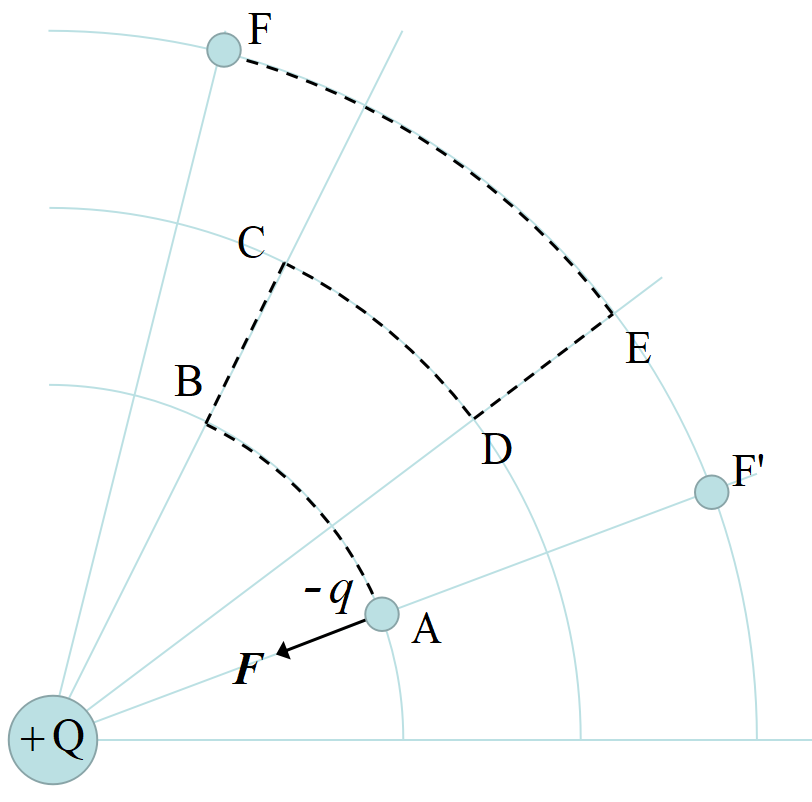
図のようにA地点からF地点まで\(-q~\)の電荷を運ぶとする。電荷は\(+Q~\)の電荷からクーロン力\(\Vec F\)を受けている。AからFに至る経路は多々あるが, 例えばAからBに電荷を移動させるのに力は不要である。すなわちエネルギー(力×距離)は不要であり, エネルギーが必要なのは, B→C,D→Eの区間のみである。従って \(-q~\)の電荷をAからFへ運ぶエネルギーは, 経路によらずA→F’まで運ぶエネルギーと等しい。摩擦力とか速度に比例する抵抗力とかが働けば, 移動させるために必要なエネルギーが経路によって異なるのは明らかであろう。
図のクーロン力のような力が保存力である。また電荷\(+Q~\)を地球の質量\(~M~\)に置き換えて\(6,400Km\)の彼方に配置し, 電荷\(-q~\)を質量\(~m~\)に置き換えればおなじみの\(\ F = mg\)となる。
すなわち重力も保存力である。バネの力は逆2乗則には従わないが, A→B,C→Dの移動にはエネルギーを必要とせず, 同様な保存力であるのは分かるだろうか?
エネルギー保存則(1) 重力位置エネルギー
先ずは高校物理のおさらいから。
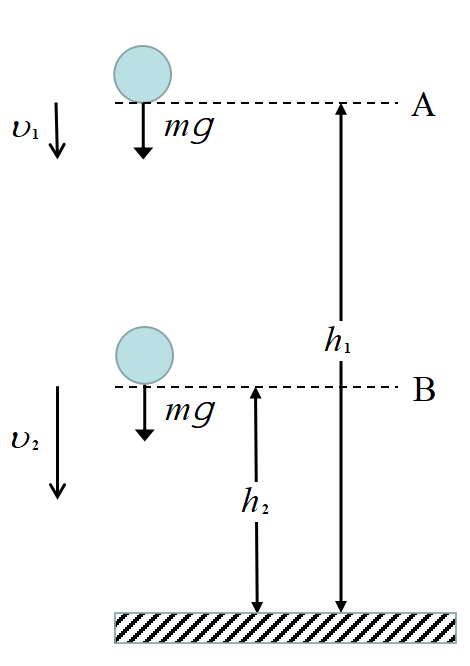
図のような条件で物体がA→Bと落下するとき
\[\upsilon_{2}^{2}-\upsilon_{1}^2=2g(h_{1}-h_{2})\]
である。両辺に\(\frac{1}{2}m\)をかけて
\[\frac{1}{2}m\upsilon_{2}^{2}-\frac{1}{2}m\upsilon_{1}^2=mg(h_{1}-h_{2})\]
を得る。左辺は運動エネルギーの増加, 右辺は重力が物体に与えたエネルギー(力×距離)である。
エネルギーが(力×距離)は
プロローグを参照されたし。
Aの状態, Bの状態に整理し直せば
\[K=\frac{1}{2}m\upsilon_{1}^{2}+mgh_{1}=\frac{1}{2}m\upsilon_{2}^2+mgh_{2}\]
となって, 運動エネルギーと位置エネルギーの和は一定で時間によらない。すなわち「エネルギー保存則」が得られる。\(K~\)を力学的エネルギーという。
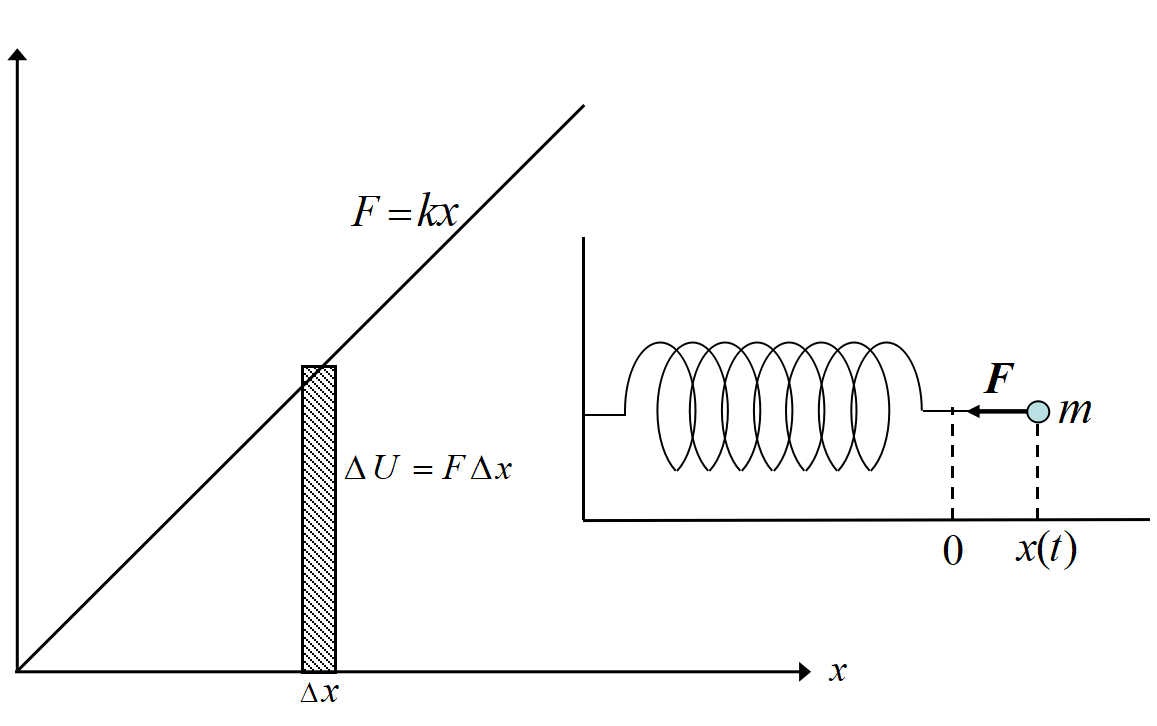
エネルギー保存則(2) バネの弾性力位置エネルギー
フックの法則\(F=-kx\)より, バネを\(\triangle x\)だけ縮めた(あるいは伸ばした)時, バネに蓄えらるエネルギー(力×距離)は
\[\triangle U=F\x \triangle x\]
なので, バネの弾性力位置エネルギーは図の面積積分で
\[U=\frac{1}{2}kx^{2}\]
と表される。バネ定数\(~k~\), 重りの質量を\(~m~\)として, 振動の中心からの変位を\(x(t)\)とすると,
\[x(t)=Asin\omega t\]
\[\omega=\sqrt{\frac{k}{m}}\]
で表される。ここで
\[\upsilon = \frac{dx}{dt}= \omega Acos\omega t\]
であるから,
\[\begin{align}
K &=\frac{1}{2}m\upsilon^{2}+\frac{1}{2}k\ x^{2} \\
&=\frac{1}{2}m \omega^{2}A^{2}cos^{2} \omega t +\frac{1}{2}kA^{2}sin^{2} \omega t \\
&=\frac{1}{2}m \frac{k}{m}A^{2}cos^{2} \omega t +\frac{1}{2}kA^{2}sin^{2} \omega t \\
&=\frac{1}{2}kA^{2}
\end{align}\]
となり, 時間によらず一定である。
ポテンシャルの導く力・勾配・\(\bm{gradient}\)・保存ベクトル場
空間の各点\((x,y,z)\)に対して値を一つ返すスカラー関数\(\phi(x,y,z)\)の勾配(\(gradient\))は
\[grad\phi =\nabla\phi = \dd{\phi}{x}\bm{i} +\dd{\phi}{y}\bm{j} +\dd{\phi}{z}\bm{k} \tag{1} \]
と定義される。空間の各点で向きや大きさを変えるベクトルを表すので
ベクトル場である。
\(\nabla\)をナブラ演算子という。なお\(~grad\phi =\nabla\phi~\)であるが, \(grad\phi =-\nabla\phi~\)とする書き方もある。物理では主に後者を用いるが, 暫くは数学流のー(マイナス)をつけない方法で説明を続ける。
この\(\nabla \phi\)が何を表すか, スカラー関数
\[\phi(x,y,z)=\frac{1}{\sqrt{x^2+y^2+z^2}}=\frac{1}{r}\]
について考えてみよう。なぜこの関数かというと, 重力の位置エネルギー, クーロン力の位置エネルギーがこの形(\(~r~\)に逆比例する)であることが分かっているからである。いきなり\(\frac{1}{r}\)を微分することは難しいので, 先ず
\(r =\sqrt{x^2+y^2+z^2}~\)の勾配, \(\nabla r \)を計算してみる。
\[
\begin{align}
\dd{r}{x}&=\dd{}{x}\sqrt{x^2+y^2+z^2}=\frac{1}{2} \frac{2x}{\sqrt{x^2+y^2+z^2}}
=\frac{x}{r}\\
\dd{r}{y}&=\frac{y}{r}\\
\dd{r}{z}&=\frac{z}{r}
\end{align}
\]
より,
\[\nabla r =\frac{x}{r}\bm{i}+\frac{y}{r}\bm{j}+\frac{z}{r}\bm{k}=\frac{1}{r}(x\bm{i}+y\bm{j}+z\bm{k})=\frac{\bm{r}}{r}
\]
これを使って,
\[
\begin{align}
\dd{}{x}\left(\frac{1}{r}\right)&=\dd{r}{x}\dd{}{r}\left(\frac{1}{r}\right)
=\frac{x}{r}\left(-\frac{1}{r^2}\right)=-\frac{x}{r^3}\\
\dd{}{y}\left(\frac{1}{r}\right)&=-\frac{y}{r^3}\\
\dd{}{z}\left(\frac{1}{r}\right)&=-\frac{z}{r^3}\\
\end{align}
\]
すなわち,
\[
\nabla\left(\frac{1}{r}\right)=-\frac{x}{r^3}\bm{i}-\frac{y}{r^3}\bm{j}-\frac{y}{r^3}\bm{k}=-\frac{\bm{r}}{r^3}=-\frac{1}{r^2}\frac{\bm{r}}{r}
\]
である。スカラー関数\(~\displaystyle \phi(x,y,z)=\frac{1}{\sqrt{x^2+y^2+z^2}}=\frac{1}{r}~\)の勾配は\(~r^2~\)に逆比例し, 中心に向かうベクトル, すなわち万有引力, クーロン力を表すベクトルを与える。\(~\phi~\)をこのベクトル場の
スカラーポテンシャルと呼ぶ。特にベクトル場が保存力を与える時, このベクトル場を
保存ベクトル場と呼ぶ。
では保存力を与える\(~\phi(x,y,z)\)とは何か?「ポテンシャル」という名称をあたえたので, もう気付いていると思うが,
重力の位置エネルギーに相当する物理量である。係数, 符号は後で正確に記述する。
ここで保存ベクトル場\(~\Vec A~\)を, 点\(M_0\)から点\(M_1\)まで, 内積を取って線積分してみる。全微分
\[d\phi=\dd{\phi}{x}dx +\dd{\phi}{y}dy +\dd{\phi}{z}dz \]
の関係を使うと,\(\displaystyle \nabla\phi = \left(\dd{\phi}{x}, \dd{\phi}{y}, \dd{\phi}{z}\right)\), \(d\bm{r}=(dx,dy,dz)~\)だから
\[
\begin{align}
\int_{M_0}^{M_1}\Vec A\cdot d\Vec r&=\int_{M_0}^{M_1}\nabla \phi \cdot d\Vec r \\
&=\int_{M_0}^{M_1} \left(\dd{\phi}{x}dx+\dd{\phi}{y}dy+\dd{\phi}{z}dz\right)\\
&=\int_{M_0}^{M_1}d\phi \\
&=\phi(M_1) - \phi(M_0)
\end{align}
\]
となる。ベクトル場\(\Vec A\)が力\(\Vec F~\)を表すとすれば, 始点と終点の間の
力×
距離の合計は経路によらず, 積分の始点と終点の値だけで決まることになる。
このスカラーポテンシャルが
ポテンシャルエネルギー, 位置エネルギーと呼ばれるものである。
(注:ポテンシャルはあるがそれが位置エネルギーではない場合もある。(原島鮮 力学p82))
勾配ベクトル(\(~grad\phi \))はポテンシャル一定の面(等位面)と直交する
電磁気学で, 電場ベクトル\(\Vec E~\)は等電位面に垂直であるとよく聞いたであろう。等電位面はスカラーポテンシャル\(~\phi (x,y,z)=c~\)(\(c\)は定数)の成す面であり, 電場ベクトル\(\Vec E~\)は\(~\phi (x,y,z)~\)の勾配である。以上を頭に描きながら説明しよう。
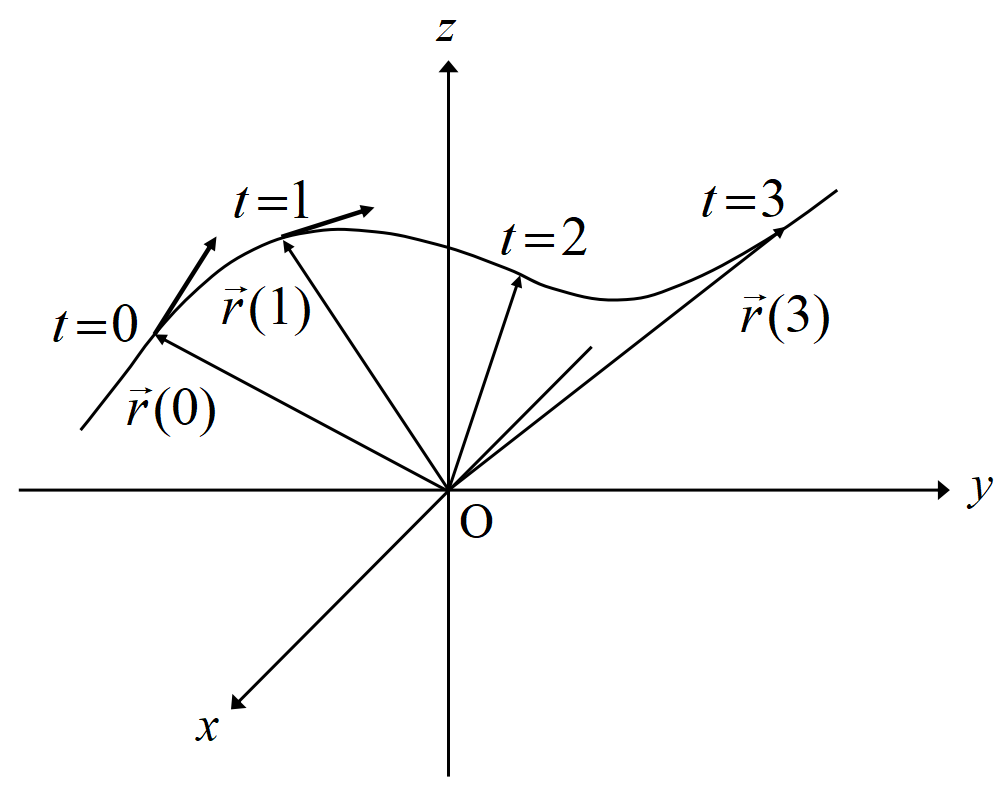
\(~\phi (x,y,z)=c~\)という等位面を考える。この等位面上の任意の曲線を\(~t~\)をパラメーターとして
\[\Vec r=x(t)\bm{i}+y(t)\bm{j}+z(t)\bm{k}\]
と表す。すなわち\(~\Vec r~\)は任意の曲線の上の任意の点の位置ベクトルである。ここで\(~\phi (x,y,z)=c~\)を\(~t~\)で微分すると,
\[\dd{\phi}{x}\dd{x}{t}+\dd{\phi}{y}\dd{y}{t}+\dd{\phi}{z}\dd{z}{t}=0 \]
これを2つのベクトルの内積と見ると,
\[\left(\dd{\phi}{x},\dd{\phi}{y},\dd{\phi}{z}\right) \cdot \left(\dd{x}{t},\dd{y}{t},\dd{z}{t}\right)=0 \tag{2}\]
ここで
\[\left(\dd{\phi}{x},\dd{\phi}{y},\dd{\phi}{z}\right) = \nabla \phi \]
また \(\Vec r=x(t)\bm{i}+y(t)\bm{j}+z(t)\bm{k}~\)を\(~t~\) で微分した成分が
\[\left(\dd{x}{t},\dd{y}{t},\dd{z}{t}\right)=\frac{d\Vec r}{dt} \]
であるから, (2)式は
\[\nabla \phi \cdot \frac{d\Vec r}{dt} =0 \]
である。\(d\Vec r/dt~\)は等位面上の任意の曲線の接線ベクトルである。
すなわち\(~\nabla\phi~\)は等位面上の任意の曲線に垂直であるから, \(~\nabla\phi~\)は等位面に垂直である。あるいは\(~\nabla\phi~\)は\(~(x,y,z)\)が\(~(dx,dy,dz)~\)だけ変化した時, \(~\phi(x,y,z)~\)の値が最も大きく変化する方向を向いている最も急勾配のベクトルである, と言っても良い。
以上からスカラーポテンシャル \(~\phi(x,y,z)\)は
ポテンシャルエネルギー, 位置エネルギーを与え, その勾配 \(~grad \phi = \nabla \phi \)は等ポテンシャル面に直交する
ベクトル場を与える。
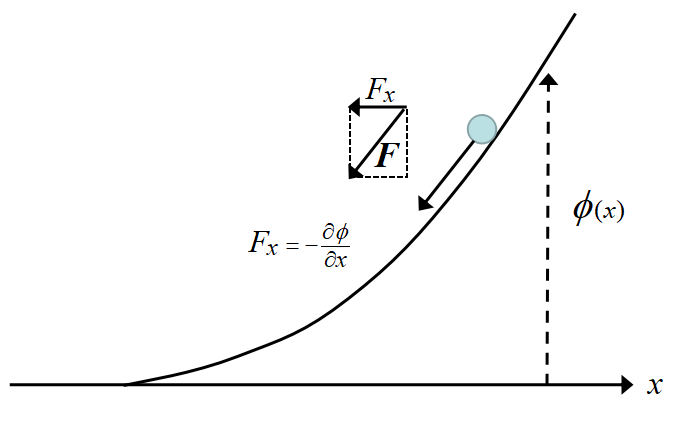
ポテンシャルの導く力
さて今までスカラー関数の勾配を\(~grad\phi =\nabla\phi~\)としてきたが, ここからは物理風に, \(grad\phi =-\nabla\phi~\)としよう。
\[\Vec F= -\nabla \phi \]
を
ポテンシャルの導く力と呼ぶ。
物理で勾配にー(マイナス)をつける理由は以下の通りである。
\(x\)方向に進むと増加するポテンシャルを考えてみよう。最も簡単な例は山登りであろうか。
傾きだけを見れば+であるが, \(\phi(x)\)に置かれた物体に働く「力」はマイナス方向に働くので, ーをつけた方が分かり易いからである。 ーにそれほど深い意味がある分けでは無い。
球面座標のナブラ演算子
(1)式はデカルト座標系のナブラ演算子である。物理で扱う力学系は球対称が多い。保存力も現実には, 万有引力, クーロン力, バネのフックの力で, 全て球対称である。球面座標(極座標も)は基底ベクトル
\(\bm{e}_r,\bm{e}_\theta, \bm{e}_\phi~\)がころころと向きを変えるので, 特に微分操作で複雑になるが, 球対称系での表現にはメリットが多い。球面座標でのナブラ演算子は
\[\nabla=\dd{}{r}\bm{e}_r+ \frac{1}{r}\dd{}{\theta}\bm{e}_{\theta}+ \frac{1}{rsin\theta}\dd{}{\phi}\bm{e}_{\phi} \tag{3}\]
である。3次元での導出は厄介なので, 2次元極座標で求めてみる。ナブラ\(~\nabla\)は(1)より
\[\nabla= \dd{}{x}\bm i + \dd{}{y}\bm j \tag{4} \]
である。
\(f(r, \theta)\)の全微分は,
\[df= \dd{f}{r}dr+ \dd{f}{\theta}d\theta \]
両辺を\(dx\)で割って
\[\frac{df}{dx}= \dd{f}{r}\frac{dr}{dx}+ \dd{f}{\theta}\frac{d\theta}{dx} \]
\(~r~\)も\(~\theta~ \)も\(~x,y~ \)の関数なので\(~dx~\)を\(\partial x~\)にして
\[\dd{f}{x}= \dd{f}{r}\dd{r}{x}+ \dd{f}{\theta}\dd{\theta}{x} \]
\(f~\)に作用する微分演算子なので\(\partial/\partial x\)の位置を移動して
\[\begin{align}
\dd{}{x}&= \dd{r}{x}\dd{}{r}+ \dd{\theta}{x}\dd{}{\theta} \tag{5} \\
\dd{}{y}&= \dd{r}{y}\dd{}{r}+ \dd{\theta}{y}\dd{}{\theta} \tag{6} \\
\end{align}\]
を得る。\(y\)での微分も加えた。2次元極座標は
\[\begin{align}
x&=rcos\theta\\
y&=rsin\theta\\
r&=\sqrt{x^2 + y^2} \\
\theta&=tan^{-1}\frac{y}{x}\\
\end{align}\]
である。\(\dd{r}{x}\)とか\(\dd{r}{x}\)を逆行列を使って求める方法もあるが, 高校数学でも出来る。
\[\begin{align}
\dd{r}{x}&=\dd{}{x}\sqrt{x^2+y^2}=\frac{1}{2}\frac{2x}{\sqrt{x^2+y^2}}=\frac{x}{r}
= cos\theta \tag{7} \\
\dd{r}{y}&= \frac{y}{r}= sin\theta \tag{8} \\
\dd{\theta}{x}&=\frac{1}{1+\frac{y^2}{x^2}} \left(-\frac{y}{x^2}\right)=
-\frac{y}{x^2+y^2}=-\frac{r sin\theta}{r^2}=-\frac{1}{r}sin\theta \tag{9} \\
\dd{\theta}{y}&= \frac{1}{r} cos\theta \tag{10} \\
\end{align}\]
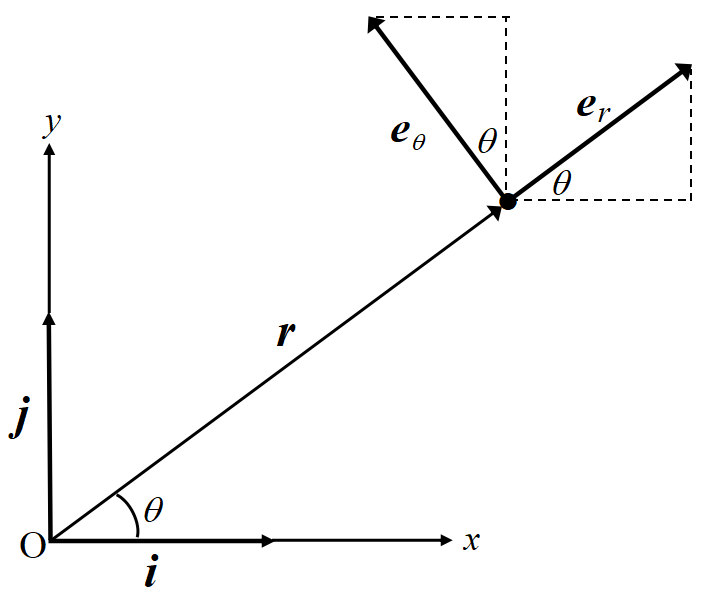
また, 2次元極座標の基底ベクトル \(\bm{e}_r,\bm{e}_\theta\)は,
\[
\begin{align}
\bm{e}_r\ &= cos\theta~\bm i+ sin\theta~\bm j \\
\bm{e}_\theta\ &= -sin\theta~\bm i+ cos\theta~\bm j \\
\end{align}
\]
である。これから逆に\(~\bm i,~\bm j~\)を\(~\bm{e}_r,~\bm{e}_\theta~\)で表し,
\[
\begin{align}
\bm i &= cos\theta \bm{e}_r - sin\theta \bm{e}_\theta \\
\bm j &= sin\theta \bm{e}_r + cos\theta \bm{e}_\theta
\end{align}
\]
を得る。(5)~(10)および, \(\bm{e}_r,\bm{e}_\theta~ \)で表した, \(\bm i,\bm j~ \)を(4)式に代入する。
\[
\begin{align}
\nabla &= \bm i\dd{}{x}+\bm j\dd{}{y} \\
&= (cos\theta\bm{e}_r - sin\theta\bm{e}_\theta)\left(cos \dd{}{r}- \frac{sin\theta}{r}\dd{}{\theta}\right)+ (sin\theta\bm{e}_r + cos\theta\bm{e}_\theta)\left(sin\theta\dd{}{r}+\frac{cos\theta}{r}\dd{}{\theta}\right) \\
&=\bm{e}_r\left(cos^2 \theta\dd{}{r}+\cancel{\frac{sin\theta cos\theta}{r} \dd{}{\theta}}
+ sin^2 \theta\dd{}{r}-\cancel{\frac{sin\theta cos\theta}{r}\dd{}{\theta}} \right)
+ \bm{e}_{\theta}\left(\bcancel{-sin\theta cos\theta\dd{}{r}}+\frac{sin^2 \theta}{r} \dd{}{\theta}
+ \bcancel{sin\theta cos\theta\dd{}{r}} + \frac{cos^2 \theta}{r}\dd{}{\theta} \right) \\
&=\bm{e}_r\dd{}{r}(cos^2\theta+sin^2\theta) + \bm{e}_\theta \frac{1}{r}\dd{}{\theta}(sin^2\theta+cos^2\theta)\\
&=\dd{}{r}\bm{e}_r + \frac{1}{r}\dd{}{\theta}\bm{e}_\theta
\end{align}
\]
ふ~!
逆行列を使ってもっとエレガントにやる方法もあるが, 一回は泥臭くやってみるのも良いかと。
球面座標で\(~r→r, \theta→90°, \phi→\theta~\)とすれば2次元極座標となる。
球面座標ナブラを使ってポテンシャル関数の勾配を求める
上と同様の手続きで球面座標のナブラが求まる。
\[\nabla =\dd{}{r}\bm{e}_r + \frac{1}{r}\dd{}{\theta} \bm{e}_\theta +\frac{1}{r sin \theta}\dd{}{\phi}\bm{e}_\phi \]
このナブラを重力の位置エネルギー
\[U = -G\frac{Mm}{r} \tag{11} \]
に作用させてみよう。
\[\begin{align}
\Vec F &= - \nabla \left(-G \frac{Mm}{r}\right) \\
&= - \left(\dd{}{r}\bm{e}_r + \frac{1}{r}\dd{}{\theta} \bm{e}_\theta +\frac{1}{r sin \theta}\dd{}{\phi}\bm{e}_\phi \right) \left(-G \frac{Mm}{r}\right)\\
&= + \dd{}{r}\bm{e}_r \left(G \frac{Mm}{r}\right)\\
&= - G \frac{Mm}{r^{2}} \bm{e}_r \\
\end {align} \]
となり, よく知られた逆2乗法則の万有引力となる。球面座標のナブラを作用させることで容易に求められる。
また重力の位置(ポテンシャル)エネルギーは
\[U = -G\frac{Mm}{r} \]
とー(マイナス)をつけるのが妥当であることも分かる。