電磁場のエネルギー
静電場のエネルギー 簡易解はコンデンサーでは何度も出てきた。
点電荷対のエネルギーは
\[U=\frac{1}{2}\sum_{i,j}\frac{q_iq_j}{4\pi\varepsilon_0 r_{ij}} \tag{1}\]
であった。先頭の\(~\frac{1}{2}~\)は, 各対について2度づつカウントし, 重複するので必要である。
微小体積\(~dV~\)中に微小電荷\(~\rho\,dV~\)があるとする。すると電荷対のエネルギーは
\[U=\frac{1}{2}\int_{V}\frac{\rho(1)\rho(2)}{4\pi\varepsilon_0 r_{12}}dV_1dV_2 \tag{2} \]
と書かれる。(2)式で\(~dV_2~\)についての積分はちょうど点 "1" の電位になっている。
\[\phi(1)=\int_{V}\frac{\rho(2)}{4\pi\varepsilon_0 r_{12}}dV_2 \]
すると(2)式は
\[U=\frac{1}{2}\int_{V}\rho(1)\phi(1)dV_1\]
点 "2" についてはもう現れてこないので, 1, 2の区別は不要で
\[U=\frac{1}{2}\int_{V}\rho\,\phi\,dV \tag{3}\]
と書ける。電荷\(~\rho\,dV~\)の位置エネルギーはこの電荷とその点の電位とをかけたものである。
\(~\rho\,dV \phi~\)の空間全域にわたっての積分が全エネルギーとなる。
ここでガウスの法則\(~\displaystyle div\Vec E=\frac{\rho}{\varepsilon_0}~\), および公式
\(~f(div \Vec A)=div(f\Vec A)-gradf\cdot\Vec A~\)
を用いると
\[\begin{align}
U&=\frac{1}{2}\varepsilon_0 \int_{V}(div\Vec E)\,\phi\, dV \\
&=\frac{1}{2}\varepsilon_0 \int_{V}div(\phi\Vec E)dV
+\frac{1}{2}\varepsilon_0 \int_{V}(-grad\phi)\cdot\Vec E\,dV \\
&=\frac{1}{2}\varepsilon_0 \int_{S}\phi\Vec E\cdot \bm{n}\,dS
+\frac{1}{2}\varepsilon_0 \int_{V}\Vec E(\bm{r})^2\, dV
\end{align}\]
2番目から3番目に移る時に\(~\Vec E=-gra\phi~\)を用いた。
この第1項は, \(S~\)を球面にとり, 半径\(~R~\)を大きくすると0になる。十分遠方では点電荷のように見えるはずだから, \(\phi\,~1/R, E\,~1/R^2, dS\,~R^2~\)。よって,この積分は\(R\to\infty~\)としてゼロ。従って
\[U=\frac{1}{2}\varepsilon_0\int_{V}\Vec E(\bm{r})^2dV \]
となる。単位体積当たりの静電エネルギー, すなわちエネルギー密度は
\[u_E=\frac{1}{2}\varepsilon_0\Vec E(\bm{r})^2 \tag{4}\]
となる。コンデンサーの簡単な例が一般的に成り立っているのが分かる。
電磁場のエネルギー方程式 電磁気学は(特殊)相対性理論との関わりが深く, "同時刻に成り立つということ"は注意深く取り扱わねばならない。
局所的保存則 電荷保存則\(~\nabla\cdot\bm{j}=-\partial\rho/\partial t~\)の本当の意味。
電荷の保存則は
\[\nabla\cdot\bm{j}=-\dd{\rho}{t} \tag{5} \]
であった。この式には見掛けよりずっと深い意味がある。
物質, エネルギー, 運動量が移動するとき, ある境界面を通して流れ出る, 流入する, という表現を取ることが多い。
特に電磁気学において顕著である。これには理由がある。
電荷\(~Q~\)の一部が\(~A~\)から\(~B~\)へ移動し, やがて全てが\(~B~\)へ移るとする。この時, 電荷の総和は常に一定であると, 当たり前の様に言うが, 厳密には正しくない。
電荷\(~Q~\)が\(~A~\)に存在しないことと, \(~Q~\)が\(~B~\)に存在することが「同時」に起こることが保証できないからである。互いに離れた点の「同時の瞬間」は座標系によって異なる。
電荷\(~Q_1~\)が\(~A~\)から\(~B~\)へ移動するとは言わず, 体積内の電荷が減少し, その変化が電流密度\(~\bm{j}~\)となって境界面を移動し, 別の空間で増加するという形を取る。式で書くと
\[-\frac{dQ_1}{dt}=\int\bm{j}\cdot\bm{n}da=\frac{dQ_2}{dt}\]
境界面に限れば, 相対論に照らしても電荷保存則が成り立っており, これを
局所的保存則と呼ぶ。
(5)式にはそういう意味が含まれているのである。蛇足であるが上式を
\[\frac{dQ_1}{dt}+\frac{dQ_2}{dt}=\frac{d}{dt}(Q_1+Q_2)=0 \]
と書けば, \((Q_1+Q_2)\)=一定, と普通の電荷保存則となる。
局所的保存則は電荷のみならず, エネルギーについても同様で, 電流密度\(~\bm{j}~\)と同様,
エネルギー流れ密度をベクトルで表現する。
重要なことを付け加えよう。局所的保存則は表現だけの問題ではなく, 電荷が一つの場所から他の場所へ移るとき「その間の空間に何かが起こらなければならない」ことである。電磁場のエネルギー, 電磁場の運動量を論ずると, 実際に何かが起こっていることが明らかとなる。最早, 遠隔作用だ近接作用だと言っているレベルの話ではない。ファラデーが心眼で見た世界が現実化してくる。
ポインティング・ベクトル ヘビサイドも独自に発見した。ポインティングは\(~Poynting~\), 人物名である。
前章
コイルに蓄えられる磁気エネルギーでソレノイドコイル内の静磁場のエネルギー密度を求めた。
静電場については
静電場のエネルギーで, より一般的に導いた。静磁場も, より一般的な方法は無いのだろうか?
磁荷\(~m~\)を仮定し
\[U_m=\frac{1}{2}\sum_{i,j}\frac{\mu_0 m_im_j}{4\pi r_{ij}} \]
として, 静電場と全く同じ方法をたどれば良さそうであるが, 磁荷\(~m~\)は発見されていないし, むしろ存在しないとされている。
そこで磁場をも含む「局所的保存則」による
エネルギー方程式から求めることになる。
ある領域\(~V~\)の内部から失われるエネルギーは, この面を通って流出したエネルギーに等しい。
空間\(~V~\)における電磁場エネルギーの収支, すなわち入ってくるエネルギーと出てゆくエネルギーの流れを考えることによって, 電磁場におけるエネルギーを求めてみよう。
以下はファインマン物理IV電磁波と物性 p80~90 を筆者が理解できるよう改編したものである。
なお, 普通の教科書では\(~\Vec E~\)と\(~\Vec B~\)の対称性に注目して, ファラデーの法則, およびマックスウェル・アンペールの法則から一気に
(12)式を導く。
電磁場のエネルギー密度を\(~u~\), エネルギーの流れ, すなわち流れに垂直な単位面積を単位時間に通るエネルギーの流れを\(~\Vec S~\)とする。
電流密度\(~\bm{j}~\)に相当する, このベクトル\(~\Vec S~\)は
ポインティング・ベクトルと呼ばれるものである。
電荷の保存則\(~\displaystyle \nabla\cdot \bm{j}=-\dd{\rho}{t}\)から容易に
\[\dd{u}{t}=-\nabla\cdot\Vec S\tag{6}\]
と類推できる。これが境界面に注目した, 局所的な場のエネルギー保存則である。
体積\(~V~\)の内部の場のエネルギーは
\[\int_Vu\,dV\]
であり, その減少の速さはこの積分の時間微分にー(マイナス)をつけたものである。
一方体積\(~V~\)を出てゆく場のエネルギーの流れは\(~V~\)を囲む面\(~\sum~\)について\(~\Vec S~\)の法線成分を積分したもの, すなわち
\[\int_\sum\Vec S\cdot\bm{n}\,da \tag{7}\]
である。
ここで注意しなければならないことがある。電荷保存だけならば(5)式のみで良い。
しかし, エネルギーを考えるときは, 電荷が電磁場内を移動するときの, 電荷と電磁場との間のエネルギーのやり取りを考えなければならない。
電磁場内での電荷の移動では, 物体の単位体積に対して電磁場が仕事をする。
電磁場内で1個の荷電粒子に働く力は\(~\Vec F=q(\Vec E+\bm{\upsilon}\x \Vec B)\)である。\(~\Vec F~\)をローレンツ力と呼ぶ。
電磁場が粒子に対して仕事をする率(電磁場から失われるエネルギー率)は単位時間当たり,
\[\Vec F\cdot\bm{\upsilon}=q\Vec E\cdot \bm{\upsilon}+q\bm{\upsilon}\cdot\bm{\upsilon}\x \Vec E\]
であるが, 右辺第2項は\(~\bm{\upsilon}\x \Vec E~\)と\(~\bm{\upsilon}~\)が垂直だから 0 。すなわち磁場は仕事をしない。
単位体積に\(~N~\)個の粒子があれば, 電磁場が電荷に対して仕事をする率は, 単位時間当たり\(~Nq\Vec E\cdot\bm{\upsilon}\)となる。
\(Nq\bm{\upsilon}=\bm{j}~\)だから, \(~Nq\Vec E\cdot\bm{\upsilon}=\Vec E\cdot\bm{j}~\)である。\(~\Vec E\cdot\bm{j}~\)は単位時間に, 単位体積につき電磁場から失われるエネルギーに等しい。
ここら辺が分かりにくい人は
ジュール熱参照。
体積\(~V~\)を出てゆく場のエネルギーの流れは(7)式に\(~\Vec E\cdot\bm{j}~\)を加えて
\[\int_\sum\Vec S\cdot\bm{n}\,da+\int_{V}\Vec E\cdot\bm{j}\,dV \]
となる。エネルギー方程式は
\[-\dd{}{t}\int_{V}udV=\int_{S}\Vec S\cdot\bm{n}da+\int_{V}\Vec E\cdot\bm{j}\,dV \tag{8} \]
である。
これが電磁場のエネルギー保存則である。右辺第1項はガウスの発散定理によって体積積分に変えられるから(8)式は
\[-\int_{V}\dd{u}{t}dV=\int_{V}\nabla\cdot\Vec SdV+\int_{V}\Vec E\cdot\bm{j}\,dV \tag{9} \]
(8)→(9)では関係ないが, 一般に\(~u~\)は\(~t~\)と\(~\bm{r}~\)の関数であるから, 微分を積分記号の中に入れる時は偏微分にしなければならない。
この方程式は任意の体積について成り立つから, 積分記号を取り除き, 電磁場のエネルギー方程式として(6)式の代わりに
\[-\dd{u}{t}=\nabla\cdot\Vec S+\Vec E\cdot\bm{j} \tag{10}\]
が得られる。まだ\(~u~\)と\(~\Vec S~\)が残っているので, 全てを\(~\Vec E~\)と\(~\Vec B~\)だけで表せば, 真の電磁場のエネルギー方程式となる。
マックスウェル.アンペールの法則
\[\bm{j}=\frac{1}{\mu_0}\nabla\x \Vec B-\varepsilon_0\dd{\Vec E}{t}\]
より, \(~\Vec E\cdot\bm{j}~\)として
\[\Vec E\cdot\bm{j}=\frac{1}{\mu_0}\Vec E\cdot(\nabla\x \Vec B)-\varepsilon_0\Vec E\cdot \dd{\Vec E}{t} \tag{11}\]
を得, \(~\Vec E~\)と\(~\Vec B~\)だけになった。
ここで技巧的ではあるが, 次の式をそのまま使わせてもらおう。自分で簡単に編み出せるものではない。
ここら辺はファインマンが自慢しているところであるが, A.ゾンマーフェルトが既に使っていたようである。(FNの高校物理)
\[\nabla\cdot(\Vec B\x \Vec E)=\Vec E\cdot(\nabla\x \Vec B)-\Vec B\cdot(\nabla\x \Vec E)\]
または並べ換えて
\[\Vec E\cdot(\nabla\x \Vec B)=\nabla\cdot(\Vec B\x \Vec E)+\Vec B\cdot(\nabla\x \Vec E)\]
すると(11)式は
\[\begin{align}
\Vec E\cdot\bm{j}
&=\frac{1}{\mu_0}\Vec E\cdot(\nabla\x \Vec B)-\varepsilon_0\Vec E\cdot \dd{\Vec E}{t} \\
&=\frac{1}{\mu_0}\nabla\cdot(\Vec B\x\Vec E)+\frac{1}{\mu_0}\Vec B\cdot(\nabla\x \Vec E)-\dd{}{t}\left(\frac{1}{2}\varepsilon_0\Vec E\cdot\Vec E\right) \\
&=\frac{1}{\mu_0}\nabla\cdot(\Vec B\x\Vec E)+\frac{1}{\mu_0}\Vec B\cdot\left(-\dd{\Vec B}{t}\right)-\dd{}{t}\left(\frac{1}{2}\varepsilon_0\Vec E\cdot\Vec E\right) \\
&=\frac{1}{\mu_0}\nabla\cdot(\Vec B\x\Vec E)-\dd{}{t}\left(\frac{1}{\mu_0}\frac{1}{2}\Vec B\cdot\Vec B\right)-\dd{}{t}\left(\frac{1}{2}\varepsilon_0\Vec E\cdot\Vec E\right) \\
&=\frac{1}{\mu_0}\nabla\cdot(\Vec B\x\Vec E)-\dd{}{t}\left(\frac{1}{2}\varepsilon_0\Vec E\cdot\Vec E+\frac{1}{2\mu_0}\Vec B\cdot\Vec B\right)\tag{12}
\end{align}\]
途中2番目の式から3番目の式へ移るとき, ファラデーの法則
\(\displaystyle \nabla\x \Vec E=-\dd{\Vec B}{t}\)
を用いた。上式右辺第1項を\(~\Vec B\x \Vec E=-\Vec E\x \Vec B~\)として
\[
-\dd{}{t}\left(\frac{1}{2}\varepsilon_0\Vec E\cdot\Vec E+\frac{1}{2\mu_0}\Vec B\cdot\Vec B\right)=\frac{1}{\mu_0}\nabla\cdot(\Vec E\x\Vec B)+\Vec E\cdot\bm{j}
\]
これと(10)式(再掲)
\[-\dd{u}{t}=\nabla\cdot\Vec S+\Vec E\cdot\bm{j} \tag{10}\]
を比べて, 静電場のエネルギー密度と静磁場のエネルギー密度の和
\[u=\frac{1}{2}\varepsilon_0\Vec E\cdot\Vec E+\frac{1}{2\mu_0}\Vec B\cdot\Vec B \tag{13}\]
を電磁場のエネルギー密度,
\[\Vec S=\frac{1}{\mu_0}\Vec E\x \Vec B \tag{14}\]
を単位時間に単位面積を通過するエネルギーの流れとすれば, 場のエネルギー方程式(10)式となる。
古典的エネルギー保存則
ここで少し別の角度から見てみよう。\(\Vec E\cdot\bm{j}~\)は
荷電粒子の運動エネルギー\(~K_q~\)の仕事率\(~\Vec E\cdot\bm{j}=dK_q/dt~\)でもあるから, (12)式を
\[\frac{d}{dt}(K_q +u)=\frac{1}{\mu_0}\nabla\cdot(\Vec B\x \Vec E) \]
とし, エネルギーが出入りする境界を宇宙の無限の彼方にすると, エネルギーが流出しないのと同じだから, 右辺は 0 で, \(~K_q +u~\)は一定である。
あるいは一般的に, 完全に孤立した系では\(~K_q +u~\)は一定である, とも言える。これは正にエネルギー保存則である。
この新しいベクトル\(~\displaystyle \Vec S=\frac{1}{\mu_0}\Vec E\x \Vec B~\)を発見者の名に因んで
ポインティング・ベクトルと呼ぶ。
ポインティング・ベクトルは電磁波の進む方向に向き, 単位面積あたりの電磁波が, 単位時間に運ぶエネルギーである。
電磁場のエネルギー方程式別解一般的な教科書の導き方
「若き学徒に窮理の道を歩んでもらいたい」ファインマンの思いは伝わるが, 注意深く読まねばならない。普通の教科書の説明を知りたい読者もいると思うので紹介しておく。
ファラデーの法則, マックスウェル・アンペールの法則を夫々,
\[-\frac{1}{\mu_0}\dd{\Vec B}{t}-\frac{1}{\mu_0}\nabla\x \Vec E=0 \]
\[\bm{j}=-\varepsilon_0\dd{\Vec E}{t}+\frac{1}{\mu_0}\nabla\x \Vec B \]
と書いておく。見た目が少し違うが今までと同じであるのは分かるだろう。
\(\Vec E~\)と\(~\bm{j}~\)(2番目の式)の内積を取り, \(\Vec B~\)と1番目の式\((=0~)\)の内積を加える。
\[\begin{align}
\Vec E\cdot\bm{j}
&=-\varepsilon_0\Vec E\cdot\dd{\Vec E}{t}+\frac{1}{\mu_0}\Vec E\cdot(\nabla\x \Vec B)-\frac{1}{\mu_0}\Vec B\cdot\dd{\Vec B}{t}-\frac{1}{\mu_0}\Vec B\cdot(\nabla\x \Vec E)\\
&=-\dd{}{t}\left(\frac{1}{2}\varepsilon_0\Vec E\cdot\Vec E\right) -\dd{}{t}\left(\frac{1}{2\mu_0}\Vec B\cdot\Vec B\right)-\frac{1}{\mu_0}
\{\Vec B\cdot(\nabla\x \Vec E)-\Vec E\cdot(\nabla\x \Vec B)\} \\
&=-\dd{}{t}\left(\frac{1}{2}\varepsilon_0\Vec E\cdot\Vec E +\frac{1}{2\mu_0}\Vec B\cdot\Vec B\right)-\nabla\cdot\left(\frac{1}{\mu_0}\Vec E\x\Vec B\right)\\
\end{align}\]
で(12)式と同じ結果が得られる。\(\Vec B\x \Vec E=-\Vec E\x \Vec B~\)に注意。最初の式の右辺4項と5項の和は 0 なので加えても何も変わらない。
2番目から3番目の式に移るときは, 公式
\[\nabla\cdot(\Vec B\x \Vec E)=\Vec E\cdot(\nabla\x \Vec B)-\Vec B\cdot(\nabla\x \Vec E)\]
を逆向き(右辺→左辺)に使った。大変エレガントに求められる。
ラグランジュの分解式をいきなり出して3次方程式の解を求めるようなもので, 筆者にはエレガント過ぎて実感が沸かない。
電波と磁波のエネルギーは等しい
電磁波の
電場と磁場の間には
\[|\Vec B|=\frac{1}{c}|\Vec E|\]
の関係があった。これを見ると, 磁場は電場と比べて非常に小さい感じがする。何しろ光速\(~c~\)で割っているのだから。
\[\begin{align}
\frac{1}{2\mu_0}\Vec B^2&=\frac{1}{2\mu_0}\frac{\Vec E^2}{c^2} \\
&=\frac{1}{2\mu_0}\Vec E^2\varepsilon_0\mu_0\\
&=\frac{1}{2}\varepsilon_0\Vec E^2
\end{align}\]
意外なことに電場と磁場のエネルギー密度は等しい。つまり電磁場のエネルギー密度は
\[\frac{1}{2}\varepsilon_0\Vec E^2+\frac{1}{2\mu_0}\Vec B^2 \]
と書く必要はなく, どちらか一方を使って, \(\varepsilon_0\Vec E^2~\)または\(~\displaystyle \frac{1}{\mu_0}\Vec B^2~\)とすれば良い。
ジュール熱・荷電粒子の運動エネルギー
\(R\,[\Omega]\)の抵抗に電圧\(~V\,[V]~\)を加えて, 電流\(~I\,[A]~\)を流すとき, 単位時間当たり
\[W=IV\]
のジュール熱が発生する。中学校(小学校?)で習った電力である。抵抗の長さを\(~l~\), 断面積を\(~\triangle S~\), 抵抗中の電場\(~E~\)は一定とする。
単位体積, 単位時間当たりのジュール熱を\(~w~\), 電流密度を\(~j~\)とすると,
\[W=wl\triangle S \qquad I=j\triangle S \qquad V=El \]
これらを\(~W=IV~\)に代入して
\[wl\triangle S=j\triangle SEl \qquad w=jE \]
電場と電流がベクトルで, \(\Vec E,\,\bm{j}~\)で与えられれば, 仕事を\(~\Vec F\cdot\bm{r}~\)としたように, 単位時間, 単位体積当たりのジュール熱(電磁場が荷電粒子に与えるエネルギー)は
\[w=\Vec E\cdot\bm{j} \]
となる。また電場中の荷電粒子の運動エネルギー\(~K_g~\)は, 電荷を\(~q~\)とすれば
\[K_g=\frac{1}{2}m\upsilon^2=qV=qEl\]
である。単位時間あたり, すなわち仕事率は,
\[\frac{d}{dt}qEl=Eq\frac{dl}{dt}=Eq\upsilon=Ej\]
である。つまり\(\Vec E\cdot\bm{j}~\)は荷電粒子の運動エネルギー\(~K_q~\)の仕事率\(~dK_q/dt~\)でもある。
ジュール熱とは, 荷電粒子が電場で加速されて運動エネルギーを得て, その分だけ電磁場のエネルギーを奪い, そのエネルギーが熱になったということである。
ポインティング・ベクトルの例
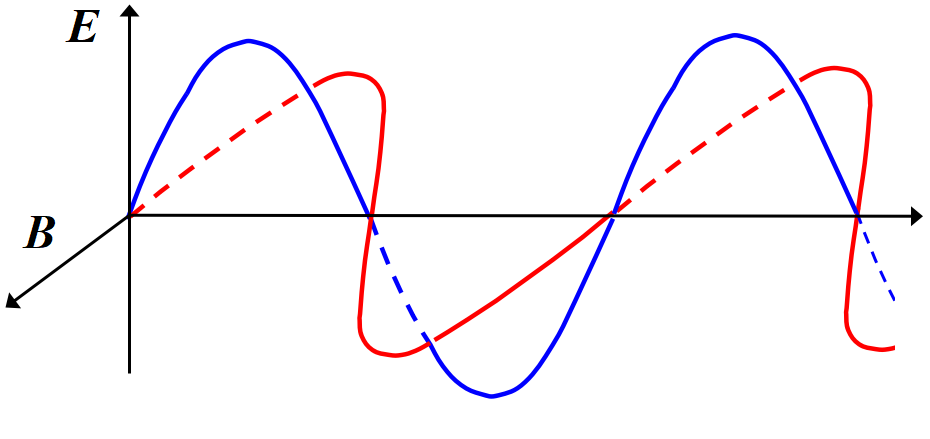
(1) 光の波
光の波では電場\(~\Vec E~\)と磁場\(~\Vec B~\)は互いに垂直で, 進行方向に対しても垂直である。\(~\Vec E~\)と\(~\Vec B~\)は
\(~1/c~\)だけの違いで,
\[|\Vec E\x \Vec B|=\frac{E^2}{c} \]
である。従って単位時間に単位面積を流れるエネルギーは\(~S=\frac{1}{\mu_0}E\x B~\)より
\[S=\varepsilon_0 cE^2 \tag{15}\]
である。電場が\(E=E_0 sin(x-ct)~\)で表されるとき, (15)式の
\(~E^2~\)の平均は
\[\langle E^2 \rangle_{av}=\frac{1}{2}E_0^2\]
単位面積当たりのエネルギーの平均の流れ\(~\langle S\rangle _{av}\)すなわち光の強度は, 電場の2乗平均の\(~\varepsilon_0 c~\)倍である。つまり
\[強度=\langle S\rangle _{av}=\varepsilon_0 c \langle E^2\rangle_{av}=\frac{1}{2}\varepsilon_0 cE^2_0 \tag{16}\]
である。これを今までの方法で求めてみよう。
光では\(~cB=E~\)であるから,
\[u=\frac{\varepsilon_0}{2}E^2+\frac{\varepsilon_0 c^2}{2}
\left(\frac{E^2}{c^2}\right)=\varepsilon_0E^2 \tag{17} \]
となる。\(E~\)は場所によって異なるから平均として
\[\langle u\rangle _{av}=\varepsilon_0\langle E^2\rangle _{av} \tag{18} \]
である。光の波は速さ\(~c~\)で伝わるから, 単位時間に1平方メートルを通るエネルギーは\(~c~\)に1立方メートル内のエネルギーをかけたものに等しい。よって
\[\langle S\rangle _{av}=\varepsilon_0 c\langle E^2\rangle _{av}=\frac{1}{2}\varepsilon_0 cE^2_0 \tag{19} \]
となり, (16)式と同じ結果を得る。
注意点を一つ上げておく。単位時間に単位面積を通るエネルギー量は,
電磁場の密度\(~\varepsilon_0E^2~\)の場合は上述のように, 光速\(~c~\)をかけ, \(\varepsilon_0cE^2~\)とする。
ポインティング・ベクトルの場合は\(~\Vec S~\)そのものが, エネルギー量を表す。\(c~\)をかける必要はない。
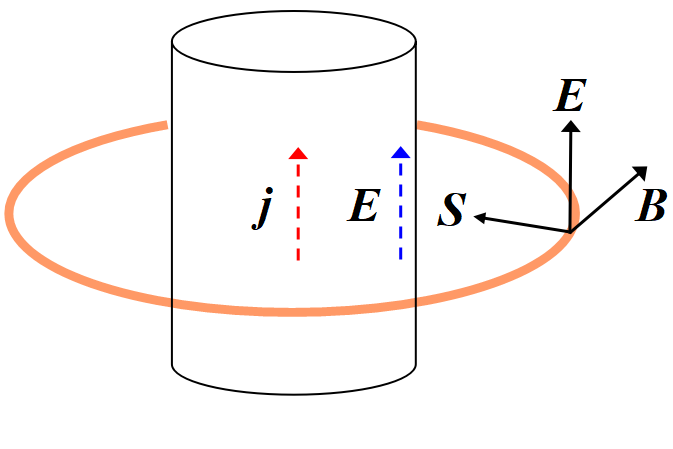
(2)電流の流れている抵抗線
以下を嚙み砕いて分かりやすく説明する力は筆者には無い。ファインマン物理IV.p89の文章をそのまま転記する。著者および訳者にはお詫び申し上げる。
抵抗があるので, 電流を流す電場がその向きに存在する。導線にそって電位差があるので, 導線のすぐ外にも, 表面に平行な電場が存在する。その上電流のために, 導線を取り巻く磁場も存在する。\(\Vec E~\)と\(~\Vec B~\)とは垂直で, そのためポインティング・ベクトルは図のように半径に沿い内側へ向いている。エネルギーは周囲から導線へと入って来る。もちろん, これは導線内で熱という形で失われるエネルギーに等しい。従って, この"奇妙な"理論の意味は, 外の場から入ってくるエネルギーによって電子は熱を作り出すエネルギーを得ているということである。直感的に言えば, 電子は導線に沿って押されることによってエネルギーを得るので, そのためエネルギーは導線に沿って流れると思うかも知れない。しかし理論によれば, 電子は実は電場によって押されるのであって, この電場ははるか遠くのどこかにある電荷に起因するものである。そして熱になるエネルギーは電子がこの電場から得たものである。
とにかく, エネルギーは遠くの電荷から広い空間を通ってきて導線の中へ入って来るのである。
(以下は筆者の追記)抵抗を電流が流れればジュール熱が発生し導体外へ逃げてゆく。この逃げたジュール熱を, 導線の側面から垂直に, ポインティング・ベクトルが補充する, と言うのである。やはり理解出来ないと言うより感覚的について行けない。
ベクトルには
極性ベクトルと軸性ベクトルがある。特に, 角運動量のように, 外積によって定義されベクトルは実体の無い軸性ベクトルが多い。
磁場\(~\Vec E~\)は実体のある極性ベクトルであるが, 磁場\(~\Vec B~\)は実体の無い軸性ベクトルである。果たしてポインティング・ベクトル\(~\Vec S=\frac{1}{\mu_0}\Vec E\x \Vec B~\)には実体はあるのだろうか?
\(\qquad\)(極性ベクトル)×(極性ベクトル) = (軸性ベクトル)
\(\qquad\)(極性ベクトル)×(軸性ベクトル) = (極性ベクトル)
\(\qquad\)(軸性ベクトル)×(軸性ベクトル) = (軸性ベクトル)
という関係がある。ポインティング・ベクトル\(~\Vec S~\)は実在するベクトルである。ファインマンは正しい。ひょっとして新発見かもと考えた自分が浅はかであった。
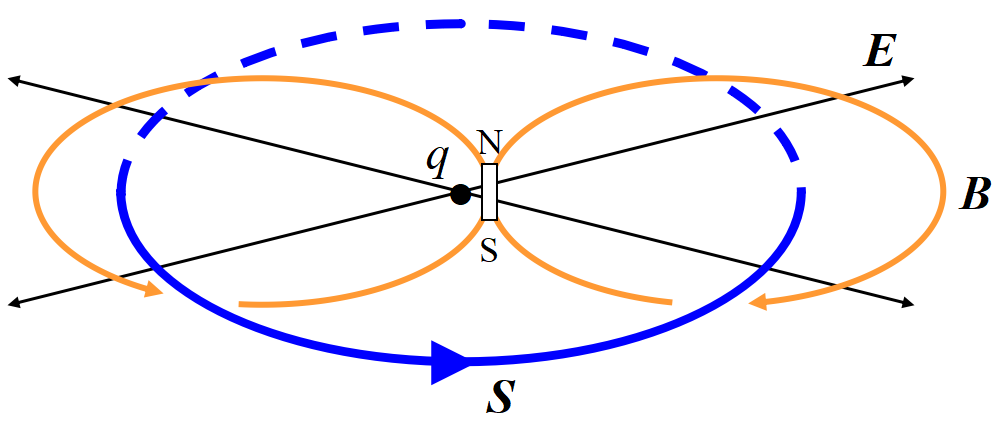
(3) 静止している磁石と電荷
接近した, 全く動かない1つの電荷と1つの磁石がある。電荷は周りに電場\(~\Vec E~\)を産み出し, 磁石は磁場\(~\Vec B~\)を産み出す。結果としてエネルギーの流れである, ポインティング・ベクトル\(~\Vec S=\frac{1}{\mu_0}\Vec E\x \Vec B~\)が存在する。
しかし, 全てが静止しているからエネルギーの変化は無い。ポインティング・ベクトル\(~\Vec S~\)はぐるぐる回っているだけである。我々の直感, 常識は極めて制限された体験から来ているようである。
電磁波の平均エネルギー密度
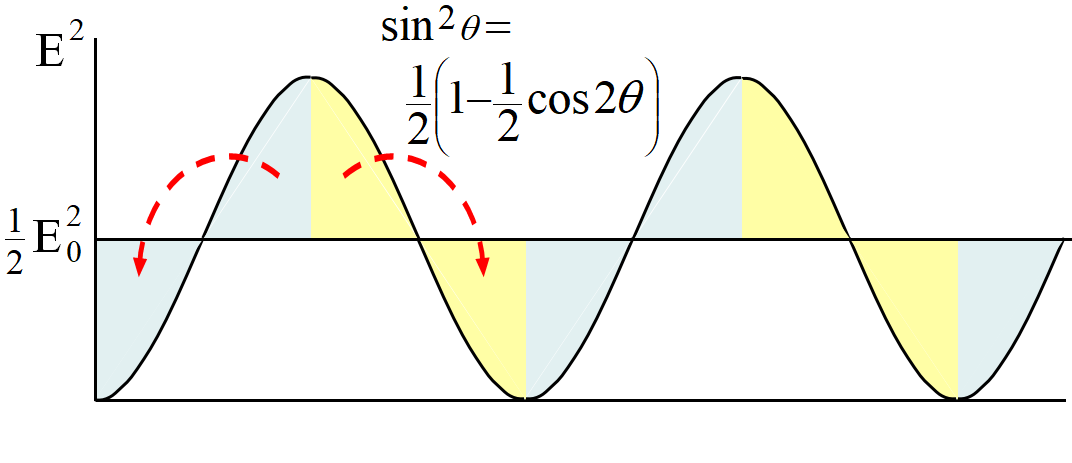
\(E=E_0 sin(x-ct)~\)の時, 電場のエネルギー密度\(~E^2~\)は, 時間, 場所によって変動する。
このエネルギー密度の平均は, 2倍角の公式\(~cos2\theta=1-2sin^2\theta~\)を使って
\[\begin{align}
E^2&=E_0^2 sin^2(x-ct)\\
&=\frac{E_0^2}{2}\{1-cos^2 2(x-ct)\}
\end{align}\]
この曲線は, \(\displaystyle E^2=\frac{1}{2}E_0 ^2~\)の直線の上下で同じ形をしており, 点線の矢印で示したように, 山の部分を谷にはめ込むと, 平均のエネルギーは
\[\langle E^2 \rangle_{av}=\frac{1}{2}E_0 ^2\]
となる。