13歳で製本屋の使い走り。7年の奉公が明けたのち, 科学者としての道を歩み始めた。5歳から13歳まで読み書き算数の初歩を習ったのが彼の受けた教育の全てであった。独学で学び, また後進の教育にも心血を注いだ。「ローソクの科学」は青少年必読の書とされる。電気力線, 磁力線のアイデアはガウス, リーマン, トムソン(ケルビン卿), そしてマックスウェルに数学的定式化の基礎を与えた。数々の偉大な発見をしたが, 数学の知識不足は本人も無念だったようで「生まれ変わったら数学に秀でた科学者になりたい」と言ってこの世を去った。150年前のことである。もう生まれ変わって, どこかで大きな働きをしているのだろうか?
ファラデー・ノイマンの誘導式 ローレンツ力の解釈に微妙な差が!
電流が磁場から受ける力(1) アンペールの法則
距離\(~R~\)だけ離れた2本の平行導線(電流\(~I_1, I_2~\))の, 長さ\(~l~\)部分に働く力は
\[F=\frac{\mu_0}{2\pi}\frac{I_1 I_2\,l}{R}\]
であった。電流\(~I_1\)が距離\(~R~\)の点に作る磁場は\(~\displaystyle B=\frac{\mu_0}{2\pi}\frac{I_1}{R}\)だから
\[\begin{align}
F&=\frac{\mu_0}{2\pi}\frac{I_1}{R}I_2\,l \\
&=B I_2\,l\
\end{align}\]
と見れば, 電流\(~I~\), 長さ\(~l~\)の導線が磁場\(~B~\)から受ける力は
\[F=I B\,l\tag{1}\]
である。
電流が磁場から受ける力(2) ローレンツ力
磁場\(~B~\)中の, 断面積\(~S~\), 長さ\(~l~\)の導線中を,\(+e~\)の電荷が速さ\(~\upsilon~\)で移動している。電荷の密度を\(~n~\)とする。
電荷1個に働くローレンツ力は\(~F=e\upsilon B~\)で, 総数は\(~nS\,l~\)であるから, 導線に働く力は\(F=n S\,l\cdot e\upsilon B ~\)である。
電流は\(I=en\upsilon S~\)と表されるから
\[F=IB\,l\]
となって(1)式と同じ結果を得る。
2本の平行導線の間の力は, アンペール自身は電荷に働く力を想像していたようである。然し, 運動する電荷に働くローレンツ力が定式化されたのは1895年である。1820年代では, 磁場と磁場の相互作用とか, 電流が磁場から力を受けるとか, どこかすっきりしない表現を取らざるを得なかった(と思う)。ただ
場の理論の先取りと言えなくもないが。
導線間の力の2通りの導出が一致したのは偶然ではなく, 曖昧とした電流間の相互作用が, ローレンツ力として極めて明瞭に再認識されたと考えればよい。ところが次に述べる電磁誘導とローレンツ力の間には謎が残る。
ファラデー・ノイマンの誘導式
ファラデーの電磁誘導の法則を\(\displaystyle V=-\frac{d\Phi}{dt}\)とする書籍も多い。
そしてー(マイナス)をレンツの法則と呼ぶ。\(V=-d\Phi/dt\)としたのはノイマン(\(~Franz\,Ernst\,Neumann~\)有名なノイマンではない)ということである。
ここではファラデー・ノイマンの誘導式と呼ぶ。
\[\phi=-k\frac{d\Phi}{dt}\tag{2}\]
\(\phi~\)は閉回路における起電力, \(\Phi~\)は回路を貫く磁力線の束, つまり磁束を表している。これからこの\(~k~\)が1であることを示す。正確には負電荷の電子が動くのであるが, 理解しやすくするために, \(+e~\)の電荷が動いて電流を生ずるとする。
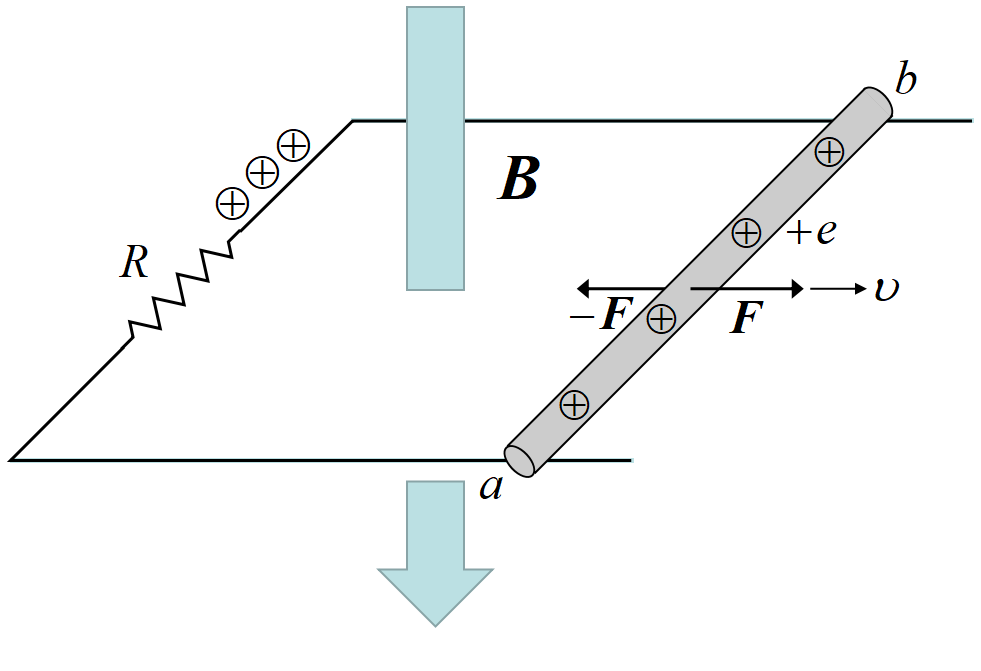
下向きの磁場\(~B~\)の中で導体棒\(~ab~\)を速度\(~\upsilon~\)で右方向へ引く。正電荷\(~+e~\)を\(~a\to b~\)の方向へ押しやる力\(~e\upsilon B~\)が生じる。ローレンツ力である。この力が正電荷を抵抗\(~R~\)へ押し込む。しかし抵抗\(~R~\)により電荷が抵抗の手前に貯まり, 電荷分布が偏り, 導体棒の\(~b~\)側の電位が上昇する。電磁誘導による(ローレンツ力により, 正の電荷を\(~a\to b~\)の方向に押しやる)誘導起電力と, 抵抗の手前の電荷分布の偏りによる(\(~b\to a~\)の方向に生じる)電位差は瞬時につり合う。
\(~a~\)と\(~b~\)のどちらの電位が高いか迷う生徒が多い。今の場合, 導体棒は電池のようになっており, \(~b~\)側が+(プラス)極である。
さて, この電池の電圧であるが, ローレンツ力は\(~e\upsilon B~\)であるから, 電荷\(~+e~\) に電場\(~E=\upsilon B~\)が作用していると考えて良い。
長さは\(~l~\)だから導体棒には
\[\phi=E\x l=\upsilon B\,l\]
の電位差が発生している。今度は(2)式で\(~\phi~\)を求めてみよう。
\(\triangle t~\)の間に磁束は\(~B\x \triangle S=B\x l\x \upsilon\triangle t~\)だけ変化するから
\[\phi=-k\frac{d\Phi}{dt}=-kB\,l\x \upsilon=-k\upsilon B\,l\]
同じ装置だから発生する起電力は同じはずである。電場の向きを考えて
\[k=1\]
と結論づけられる。上図のような特殊例ではなく, 一般の場合は, 例えばEMANの電磁気学電磁誘導を参照されたい。
(1)式で表される, 電流が磁場から受ける力では, ローレンツ力による解釈は, アンペールの法則による解釈をさらに明確にしたものであった。両者の間には何の矛盾もない。一方電磁誘導ではローレンツ力と磁束の変化が奇妙に一致した。この2つは異なる物理現象であり, 一致は自明ではない。古典電磁気学\(~Maxwell~\)方程式では解決できない問題である。
上述の例で, 注意すべき点に触れておく。
抵抗の部分では\(~I=\phi/R~\)で定まる電流\(~I~\)が流れる。この電流により磁場中におかれた導体棒\(~ab~\)には速度ベクトル\(~\upsilon~\)とは逆向きの力
\[F'=IB\,l=\frac{\upsilon B\,l}{R}B\,l=\frac{\upsilon B^2l^2}{R}\]
を生じる。この力\(~F'~\)と, 元々導体棒を引いていた力\(~F~\)とがつり合い\(~F'=F~\)となり定常状態が実現される。
つまり, 導体棒を引く力\(~F~\)が大きければ棒の速度\(~\upsilon~\)は大きくなり, 力\(~F~\)が小さければ速度\(~\upsilon~\)は小さくなる。また, 導体棒を早く動かそうとすると大きな力が必要になり、棒をゆっくり動かせば力は小さくても良い。
突然\(~R=0~\)とすると電流が急増し, 巨大な力が発生して, 導体棒はストップする。ただし, 本当にそうなるかどうかは, 既存磁場を打ち消す方向に巨大な磁場が発生するから不明である。入試問題でも見たことがないので, それなりに難しい問題であるのかも知れない。
従って上述の問題を取り扱う時は, \(I=\phi/R~\)で定まる電流が作る磁場が, 磁場\(~B~\)と比べて十分に小さいという条件が必要である。
磁束の変化を伴わない誘導起電力
上記の例では, 繋がりは必ずしも明確ではないが, ファラデー・ノイマンの誘導式とローレンツ力は等価であるような印象を与える。本当にそうであろうか?次の例はファインマン物理III電磁気学17-2に示されている
例外, すなわちファラデー・ノイマンの誘導式が適用できない例である。入試にも頻出する。ただし, 特にネット記事ではファラデー・ノイマンの誘導式で解いてしまっている例が多い。
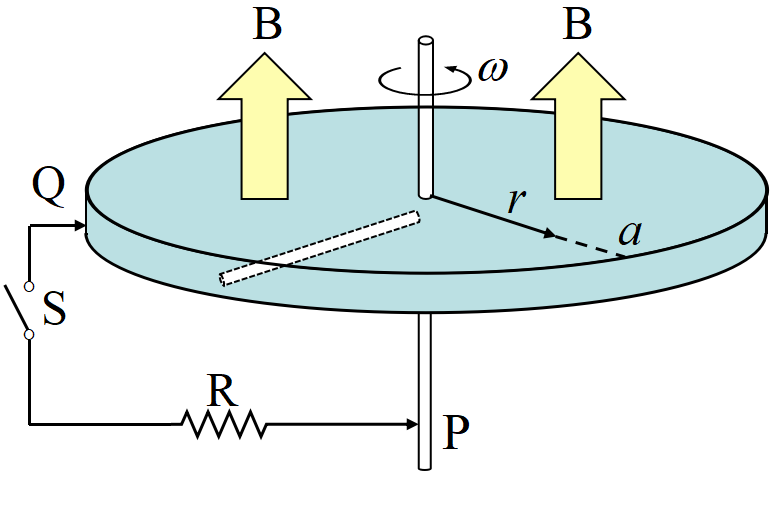
半径\(~a~\)の円板と中心の回転軸は共に導体で出来ていて, これを一定の速度\(~\omega~\)で回転させる。回転軸と円板の縁にP点とQ点で導線を接触させ, スイッチ\(~S~\)を通じて抵抗をつなぐ。円板には一様な磁場\(~B~\)が図の向きにかかっている。\(~S~\)は初め開かれ, 回路の抵抗値を\(~R~\)とする。
(1) 円板と共に回転する自由電子はローレンツ力を受け円板の中心に向かおうとする。
(2) 円板の中心には負の電荷が, 縁には自由電子がいなくなった正電荷が現れ, 縁から中心へと向かう電場が発生する。
(3) ローレンツ力による電子の移動は, 発生した電場から受ける静電気力と釣り合うまで続く。
電子の速さは\(~\upsilon=r\omega~\)であるから, ローレンツ力は
\[f=e\upsilon B=er\omega B\]
静電気力との釣り合いより
\[eE=er\omega B \quad \therefore E=\omega Br\]
中心と縁との電位差は
\[V=\int_{0}^{a}Edr=\int_{0}^{a}\omega Br\,dr=\frac{1}{2}\omega Ba^2\tag{3}\]
となる。入試問題集には「電磁誘導」の項目に書かれているが, 磁束の変化にはよらない起電力である。
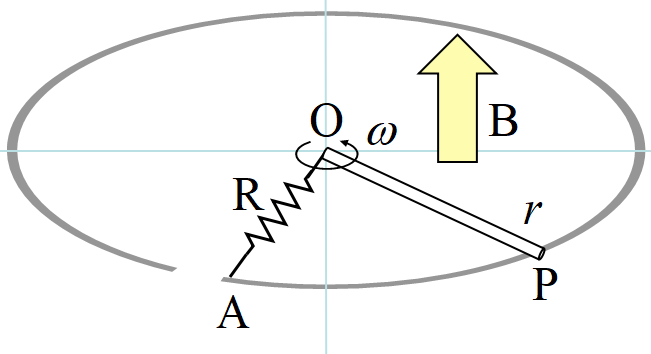
ところで次図の問題も頻出である。一部をカットした円形レールの上を, 角速度\(~\omega~\)で回転させながら金属棒を滑らせる。この時\(~R~\)に流れる電流を求めよというものである。
起電力を求めると, 扇形OAPの面積は\(\displaystyle\frac{1}{2}r^2\omega t\)だから
\[V=-\frac{d\Phi}{dt}=-\frac{1}{2}\frac{Br^2\omega t}{dt}=-\frac{1}{2}Br^2\omega \]
で(3)式と同じ結果を得る。ついでであるが, ローレンツ力を使った解法は以下の通り。
金属棒中の自由電子の速度は中心で0, 外周で\(~r\omega~\)なので平均として\(~r\omega/2~\)とする。
ローレンツ力は\(~F=er\omega B/2~\)。平均の電場\(~E=r\omega B/2~\)より, 中心と周辺の電位差は, \(~\displaystyle V=\frac{r\omega B}{2}\x r=\frac{Br^2\omega}{2}~\)。
さてこの例を用いれば, 回転導体円板もローレンツ力を使った解法があるのではないかとしばらく考えてみた。ファインマンの教科書の間違いを見つけられるかも!
実際, 回転する導体円板に, 円形レールと全く同じ式を適用している記事も多いが, 間違いである。
プラスチック製の回転円板の中に金属棒(図の白線部分)を埋め込み, 円板を回転させる。(電極が無いので測定は不可能だが)ローレンツ力による電荷の偏りによって, 導体棒中に電場を生じるのは容易に理解される。円板を導体にしたのは接点\(~Q~\)を確保するためだけである。プラスチック円板の中の導体棒が磁場中を回転するだけならば, 敢えて回転の必要はなく, 直線移動でも良い。図をみると, いかにも円板が磁場を横切っていて, 円形リングのような電磁誘導現象が起きているかのような錯覚を与える。導体棒が磁場中を移動しているだけなので, ファラデーの誘導法則とは言い難い。ファインマンの教科書が正しいのは分かったが, 何か拍子抜けである。
回転導体円板にファラデー・ノイマンの誘導式を適用してはいけないのは分かったが, それでもローレンツ力を考えた場合と結果は一致する。何故だろうか?特殊相対性理論がこの矛盾を解決する。
ファラデーの誘導法則
閉回路において起電力を\(~\phi~\), 磁束を\(~\Phi~\)とすると, 夫々以下の様に記述される。
\[\phi=\int_{C}\Vec E\cdot d\bm{s}\]
\[\Phi=\int_{S}\Vec B\cdot\bm{n}dS \]
\(C~\)は任意の閉曲線で\(~S~\)はそれを縁とする閉曲面である。(2)式に当てはめると,
\[\int_{C}\Vec E\cdot d\bm{s} =-\frac{d}{dt}\int_{S}\Vec B\cdot\bm{n}dS\]
左辺をストークスの回転定理で置き換え, 右辺の微分を積分の中に入れると,
\[\int_{S}\nabla \x \Vec E\cdot\bm{n}dS= \int_{S}-\frac{\partial}{\partial t}\Vec B\cdot\bm{n}dS\]
これが任意の空間で成り立つのであるから*(下記注)
\[\nabla \x \Vec E= -\dd{\Vec B}{t}\tag{3}\]
となる。これが一般に
ファラデーの誘導法則と呼ばれ, \(Maxwell~\)方程式の一部である。
*任意の空間で成り立つためには, 実は
\[\nabla\cdot \Vec B=0\]
が成り立つ事が必要である。(石井俊全 一般相対性理論を一歩一歩数式で理解する。p92より転記)
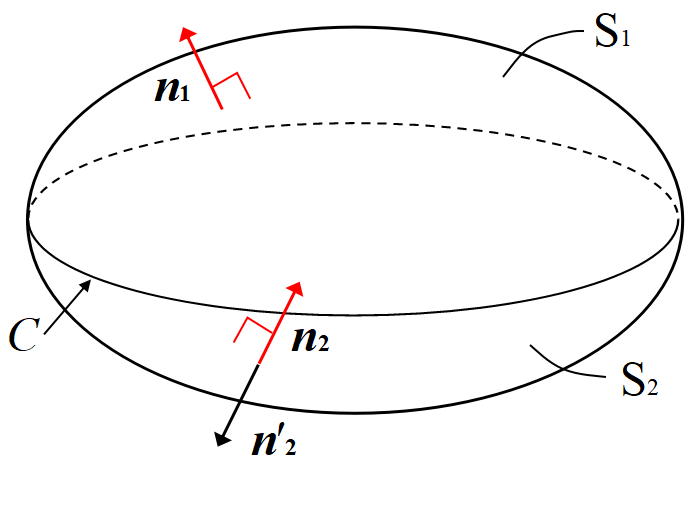
\(C~\)を境界に持つ2つの曲面\(~S_1, S_2~\)において, \(~S_1, S_2~\)で囲まれる部分の領域を\(~V~\)とする。\(S_1, S_2~\)に関して, \(C~\)の向きから右ねじの向きに単位法線ベクトル\(~\bm{n_1},\bm{n_2}~\)を定める。ここで\(\bm{n'_2}=-\bm{n_2}\)とおくと,\(\bm{n_1}\)と\(\bm{n'_2}~\)は\(~V~\)に対して外側を向いたベクトルになる。ガウスの発散定理より
\[\int_{S_1}\Vec B(\bm{x})\cdot \bm{n_1}(\bm{x})dS
+\int_{S_2}\Vec B(\bm{x})\cdot \bm{n'_2}(\bm{x})dS
=\int_{V}div\Vec B(\bm{x})dV=0 \]
仮定\(~div\Vec B(\bm{x})=0~\)を用いた。これより
\[\int_{S_1}\Vec B(\bm{x})\cdot \bm{n_1}(\bm{x})dS
=-\int_{S_2}\Vec B(\bm{x})\cdot \bm{n'_2}(\bm{x})dS
=\int_{S_2}\Vec B(\bm{x})\cdot\bm{n_2}(\bm{x})dS \]
すなわち, \(S~\)の取り方によらず, \(\Vec B(\bm{x})\)の面積分の値が定まる。
静電場のガウスの法則に対応するものとして, 静磁場における\(~\nabla\cdot \Vec B=0~\)は, 単極磁荷(モノポール)が存在しないことから導かれるとされる。
ところが磁荷は存在しないのではなく見つかっていない。あるいは, モノポールが無くても観測事実は説明できる位のことである。モノポールが存在しないと証明された分けでもなく, 実際にモノポールの探求を行っているチームがある。時折り「モノポール発見!」の記事もみられる。
筆者は長年この点, すなわち「モノポールはあってもなくても電磁理論は構築できるのに, 何故\(~\nabla\cdot \Vec B=0~\)」に疑問を抱いていた。
\(~\nabla\cdot \Vec B=0~\)をもっと合理的に説明できないのか?
上述の説明は, \(~\nabla\cdot \Vec B=0~\)は, これが成り立てば(2)式が任意の空間で成り立つというもので, 十分条件で, 必要条件ではない。
然し, 「モノポールが見つかっていないので\(~\nabla\cdot \Vec B=0~\)とする」よりはましなような気がするが, こだわりすぎであろうか?
コイルの磁気エネルギー コンデンサーが静電エネルギーを蓄える様に, コイルは磁気エネルギーを蓄える。
コイルの自己インダクタンス
コイルを流れる電流が変化すると, コイルを貫く磁束が変化するため, コイル自身に誘導起電力が発生する。この現象を
自己誘導という。自己誘導起電力は電流の変化を妨げる向きに発生するので,
逆起電力という。逆起電力は
\[V=-L\frac{\triangle I}{\triangle t} \tag{4}\]
で, 比例定数\(~L~\)を自己インダクタンスという。
LC共振回路 振動するのは電流ではなく, 電場と磁場である。
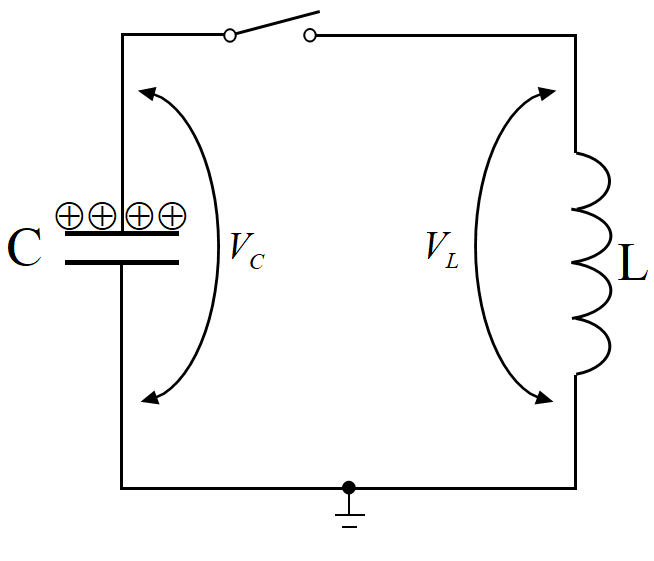
コンデンサーを電池で充電したのち, スイッチを閉じる。コンデンサーの電圧を\(~V_C\), コイルの電圧を\(~V_L~\)とすると, キルヒホッフの法則より
\[V_C+V_L=0\tag{5}\]
電流の向きを時計回りに取ると, コンデンサーの正の電荷が減少するとき, 電流が + になるから
\[I=-\frac{dQ}{dt}\]
となる。これは電荷保存則でもある。
\(\displaystyle V_C=\frac{Q}{C}, V_L=-L\frac{dI}{dt}=+L\frac{d^2Q}{dt^2}\)を(5)式に代入すると
\[\frac{Q}{C}+L\frac{d^2Q}{dt^2}=0\]
\[\frac{d^2Q}{dt^2}=-\frac{1}{LC}Q\]
となり, バネの単振動と同じ微分方程式となる。電荷\(~Q~\)が単振動解なので, 電流も同じ単振動で
\[I(t)=I_0 sin(\omega t+\delta),\quad \omega=\frac{1}{\sqrt{LC}}\]
これが「振動電流」であると多くの教科書に書いてある。筆者も長らく電流が振動していると理解していた。
ところが導体中の電流, 自由電子の移動速度は\(~0.01 cm/sec~\)程度である。とても振動できるような速さではない。
では何が振動しているのか? コンデンサーの電場と, コイルの磁場, 言い換えると電場のエネルギーと磁場のエネルギーが振動しているのである。
コイルに蓄えられる磁気エネルギー
コイルに電流を流そうとすると, レンツの法則により逆起電力\(~V=-L~(dI/dt)\)を受ける。電流を\(~I~\)とすると, 単位時間当たり\(~IV~\)のエネルギーを押し込むことになる。あるいは電流には
慣性があって, コイルに電流が流れ込むと解釈することもできる。
ある時間\(~T~\)の間に電流を\(~0~\)から\(~I~\)まで増加させるのに必要なエネルギーは,
\[U=\int_{0}^{T}I\left(L\frac{dI}{dt}\right)dt=L\int_{0}^{I}I\,dI=\frac{1}{2} LI^2 \tag{6}\]
である。これがコイルに蓄えられるエネルギーである。
長いソレノイドコイルに電流\(~I~\)を流した時に, 長さ\(~l~\)の部分に蓄えられる磁気エネルギーを求めてみよう。
長いソレノイドの作る磁場は
\[B=\mu_0 nI\]
であった(\(B_0\to B, L\to l~\)とした)。電流を\(~\triangle I~\)変化させると, 磁場も
\[\triangle B=\mu_0 n\triangle I\]
と変化する。ソレノイド内の磁束も変化し
\[\triangle \Phi=\triangle B\x S\x N=\triangle B\x S\x nl=\mu_0n \triangle I\x S\x nl \]
\(~N, n, l, S~\)は夫々巻き線数, 巻き線密度, ソレノイドの長さ, 断面積である。
ファラデー・ノイマンの誘導式より
\[V=-\frac{\triangle \Phi}{\triangle t}=-\mu_0 n^2 S l\frac{\triangle I}{\triangle t}=-L\frac{\triangle I}{\triangle t}\]
すなわち自己インダクタンス\(~L~\)は
\[L=+\mu_0 n^2 S l \tag{7}\]
である。ソレノイドに蓄えられるエネルギーは, (7)式を(6)式に代入して
\[\begin{align}
U=\frac{1}{2}LI^2&=\frac{1}{2}\mu_0 n^2 S l\,I^2 \\
&=\frac{1}{2}\frac{1}{\mu_0}(\mu_0 n I)^2 Sl\\
&=\frac{1}{2}\frac{1}{\mu_0}B^2 Sl
\end{align}\]
\(Sl~\)はソレノイドの体積であるから, 磁場のエネルギー密度は
\[u_m=\frac{1}{2\mu_0}B^2 \tag{8}\]
となる。
コンデンサーのエネルギー密度は
\[u_E= \frac{U}{Sd}= \frac{CV^{2}}{2Sd}=\frac{\varepsilon_0 S}{d}\cdot(Ed)^2\cdot\frac{1}{2Sd} =\frac{1}{2} \varepsilon_0 E^2 \tag{9}\]
であった。対称性の良さから\(~B=\mu_0 H~\)を使って,
\[u_m=\frac{1}{2}\mu_0 H^2 \tag{10}\]
とすることも多い。(10)式を用いると(静)電磁場のエネルギー密度は
\[u=\frac{1}{2}\varepsilon_0 E^2+\frac{1}{2}\mu_0 H^2\]
と美しく書かれ, また\(\displaystyle \frac{1}{2}\varepsilon_0 E^2 =\frac{1}{2}\mu_0 H^2\)も証明できるので(10)式の方が良いような気もする。
然し, 筆者は(8)式の方が良いと思う。理由はいずれまた。