ビオ・サバールの法則とアンペールの法則
電場と比べて磁場は分かり難い。電荷は存在するのに磁荷は存在しないことが大きな要因だと思う。磁場は
電流を介して現れる。
歴史的にも電気と磁気は別物と考えられていた時期が長かった。1600年から200年間, 電流と磁気の間には何の関係も発見されなかった。
2つの法則は同じ計算結果を与えるので等価と言える。しかし考え方は異なる。ビオ・サバールの法則は「微小電流要素\(~Id\bm{s}~\)」を「磁荷」に見立てており, クーロンの法則に酷似している。アンペールの法則も微小電流要素を用いてはいるが, 磁場を感じるのは磁石ではなく, 感じる側の微小電流の磁場である。つまり磁場と磁場の相互作用である。ガウスの法則に近い。
| |
磁力の原因となる相互作用 |
|
|
電気力の原因となる相互作用 |
| ビオ・サバールの法則 |
磁場の源:\(Id\bm{s}\) 磁力:磁場と磁石*1 |
|
クーロンの法則 |
電場の源:電荷\(Q\) 電気力:電荷と電荷 |
| アンペールの法則 |
磁場の源:\(Id\bm{s}\) 磁力:磁場と磁場*1 |
|
ガウスの法則 |
電場の源:電荷\(Q\) 電気力:電場と電荷*2 |
*1 磁場を感じるのはビオ・サバールの法則では磁石, アンペールの法則では微小電流の作る磁場
*2 電荷自身の電場(自己場)との相互作用と考えても良いが, 自己場は特異点(無限大発散)の問題があり, 電場と電荷としておいた方が無難である。
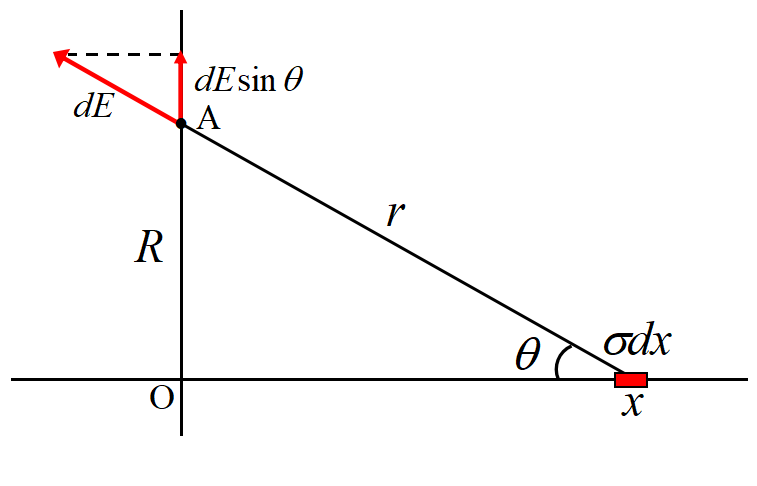
電流の作る磁場(1)ビオ・サバールの法則 その前に直線上の電荷の作る電場の計算
\(x~\)軸上の微小電荷を\(~\sigma dx~\)とする。\(\sigma~\)は電荷の線密度である。この電荷が点\(~A~\)に作る電場は
\[dE=\frac{1}{4\pi\varepsilon_0}\frac{\sigma dx}{r^2} \]
である。\(x~\)について\(~-\infty~\)から\(~+\infty~\)まで積分するわけであるが, 電場は\(~x~\)軸に垂直であろうから, 積分するのは\(~sin\theta~\)を乗じた
\[dE=\frac{1}{4\pi\varepsilon_0}\frac{\sigma sin\theta\ dx}{r^2} \tag{1}\]
で良い。取り敢えず積分してみる。
\[\begin {align}
E &=\frac{1}{4\pi\varepsilon_0}\int_{-\infty}^{+\infty}\frac{\sigma sin\theta} {r^2}dx \\
&=\frac{\sigma}{4\pi\varepsilon_0}\int_{0}^{\pi}\frac{\sin\theta}{r}d\theta \\
&=\frac{\sigma}{4\pi\varepsilon_0 R} \left[-cos \theta \right]^{\pi}_{0} \\
&=\frac{1}{2\pi\varepsilon_0}\frac{\sigma}{R} \tag{2} \\
\end{align}\]
途中, \(x=R/tan\theta\), \(dx=-R d\theta/sin^2\theta\), \(r=R/sin\theta\)を用いた。
重要なのは計算の過程ではなく, 場が(2)の形で表されるとき, 原因となる微小要素が(1)の形を取ることである。
さて1820年7月, ハンス・クリスティアン・エルステッド(Hans Christian Ørsted)が電流が磁場を作り出すことを発見した。それを知ったジャン=バティスト・ビオ(Jean-Baptiste Biot)とフェリックス・サバール(Félix Savart)は巧妙な実験によって(FNの高校物理)定常電流のまわりの磁場を測定した。そして, 直線電流\(~I~\)から距離\(~R~\)の地点に,
\[B=\frac{\mu_0}{2\pi}\frac{I}{R}\tag{3}\]
の磁場の発生を見出した。
定式化するとき, ラプラス(高名な数学者。逝去したフーリエに代わり, 若きガロアの論文を審査したが, 良く分からん!と言って却下した) の助言内容を確かめる実験まで行ってビオ・サバールの法則を確立した。ラプラスの助言は
\[dH\propto\frac{Ids\ sin\theta}{r^2}\]
で,(1)式と同じである。どうやって思いついたのだろうか?
物理量が作用するとき, その垂直成分が有効というのはよくある。角運動量\(~L=r\x m\upsilon sin\theta~\)で\(~sin\theta~\)が垂直成分を表す。\(r^2~\)は逆2乗法則。この位だったら筆者でも助言できそうだが。もっと深い理由があるのだろう。
導線上の微小な長さ\(~ds~\)を流れる電流素片\(~Ids~\)が, 距離\(~r~\)だけ離れた点に作り出す微小な磁場\(~dB~\)は
\[dB=\frac{\mu_0}{4\pi}\frac{I ds}{r^2}sin\theta\]
である。さらにこの式をベクトル表現すると電流素片\(~Id\bm{s}~\)が, そこから\(~\bm{r}~\)の位置に作る微小磁場\(~d\Vec B~\)は
\[d\Vec B=\frac{\mu_0}{4\pi}\frac{I d\bm{s}\x \bm{r}}{r^3} \tag{4}\]
である。この関係をビオ・サバールの法則と呼ぶ。
この式を用いれば, 任意の形状\(~C~\)に沿って流れる電流\(~\Vec I~\)が作る磁場は
\[\Vec B=\frac{\mu_0 I}{4\pi}\int_C\frac{d\bm{s}\x \bm{r}}{r^3}\]
で求めることが出来る。
電流の作る磁場(2)アンペールの法則 歴史的経緯はやや曖昧。
エールステッドの発表が1820年5月30日, アンペールの論文第1報は同年9月18日, ビオ・サバールの式(4)による定式化が同年10月30日である。
\(Maxwell~\)方程式に用いられる, アンペールの法則の現在の形は, 1845年数学者グラスマンによって与えられた。1820年~1845年の経緯について調べたが, はっきりしたことは分からなかった。
がともあれ, 重要なことは, クーロンの法則とガウスの法則が等価であるように, ビオ・サバールの法則とアンペールの法則は等価であることである。
アンペールの論文は, 不明な点もあるが,
(1)電流の流れる向きに対して, 磁場の向きは右ネジの法則に従う。
(2)2本の電線は, (直線)電流が平行なら引き付けあい, 電流が反平行なら反発しあう。
(3)任意の閉じた経路に沿って磁場を足し合わせた結果は, 閉じた経路を貫く電流の和に比例する。
(4)距離\(~R~\)だけ離れた2本の平行導線(電流\(~I_1, I_2~\))の, 長さ\(~l~\)部分に働く力は
\[F=\frac{\mu_0}{2\pi}\frac{I_1 I_2\ l}{R}\]
である。(1)~(4)をアンペールの法則と呼ぶ。多くの独創的な実験を行ったとあるが, 記事も少なく, 筆者には不明である。
グラスマンによって上の式は, 2本の導線の微小線要素ベクトルを\(~d\bm{x}, d\bm{y}~\)として, 電流要素間に働く力は,
\[d^2\Vec F=\frac{\mu_0}{4\pi}I_1 d\bm{x}\x I_2 d\bm{y}\x \frac{\bm{r}}{r^3}\tag{5}\]
と定式化された。ここに\(~\bm{r}~\)は微小要素間の一方から他方を見た位置ベクトルである。\(~d^2~\)となっているのは2次の微小量を明記するためである。良く用いられる。
導線1内の電子の密度を\(~n\), 平均の速度を\(~\bm{\upsilon}~\), 導線の断面積を\(~S~\)とすると, \(I_1=en\upsilon S~\)より
\[I_1 d\bm{x}=en\upsilon Sd\bm{x}=enSdx\bm{\upsilon}=q\bm{\upsilon}\tag{6}\]
が成り立つ。\(~\bm{\upsilon}~\)と\(~d\bm{x}~\)は平行なので, \(\upsilon d\bm{x}=\bm{\upsilon}dx~\)を用いた。
(6)を(5)に代入して
\[\begin{align}
d^2\Vec F
&=\frac{\mu_0}{4\pi}q\bm{\upsilon}\x \left(I_2 d\bm{y}\x \frac{\bm{r}}
{r^3}\right)\\
&=q\bm{\upsilon}\x \left(\frac{\mu_0}{4\pi}\frac{I_2 d\bm{y}\x \bm{r}}
{r^3}\right)\\
&=q\bm{\upsilon}\x d\Vec B \tag{7}
\end{align}\]
となって, \(d\Vec B~\)が(4)式と一致する。すなわち2つの法則は数学的に同等である。
アンペールは電流\(~I_1~\), \(~I_2~\)がそれぞれ磁場を作り, 磁場同士の相互作用で電線が引き合ったり, 反発したりすると考えた。
現在は高校でローレンツ力を習う。ローレンツ力を使えば磁場と磁場との相互作用とか抽象的な表現を使わなくとも良い。電流\(~I_1~\)の作った磁場の中を, 電荷を持った粒子が運動すればローレンツ力を受け, 引き付けられたり, 反発したりする。
しかしローレンツ力がはっきり形を整えたのは1895年。アンペールが試行錯誤していた70年後である。
それでも疑問は残る。ローレンツ力は何故磁場と電荷の運動方向の両方に垂直なのか?全てに満足のゆく解釈が得られるには特殊相対性理論の登場を待たねばならない。
アンペールの法則 ベクトル場による表現
(3)閉じた経路に沿って磁場を足し合わせた結果は, 閉じた経路を貫く電流の和に比例する。
という項目があった。
閉じた経路に沿って磁場を足し合わせたは
\[\oint_{C} \Vec B\cdot d\bm{s}\]
と表現出来る。するとストークスの回転定理がすぐに連想され,
\[\oint_{C}\Vec B\cdot d\bm{s}=\int_{S}\nabla\x \Vec B\cdot d\Vec S\]
となる。
閉じた経路を貫く電流の和は
\[\int_{S}\bm{j}\cdot d\Vec S\]
だろう。すると
\[\int_{S}\nabla\x \Vec B\cdot d\Vec S=\int_{S}\bm{j}\cdot d\Vec S\]
これが任意のループについて成立するというのだから,
\[\nabla\x \Vec B=\mu_0 \bm{j}\tag{8}\]
\(\mu_0\)は単位の調整のために付けた。(8)式は\(~Maxwell~\)方程式の一部である。
(8)式は, 通常はベクトルポテンシャル\(\Vec B=\nabla\x \Vec A~\)を仮定し, \(\nabla\x \Vec B~\)から求める。ここではアンペールの法則の一部をそのまま素直に置き換えて求めてみた。
アンペールの法則の応用
アンペールの法則はガウスの法則と同様, その深い物理的洞察の他に実用上のメリットも大きい。
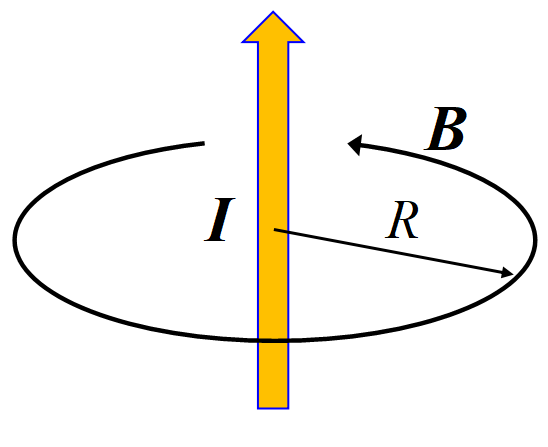
直線電流の作る磁場
\(\Vec B\cdot d\bm{s}~\)の線積分は\(~\Vec B~\)の大きさに円周をかけたもので
\[\oint_{C}\Vec B\cdot d\bm{s}=B\cdot 2\pi R \]
である。ループ内の全電流は\(~I~\)だから,
\[B\cdot 2\pi R=\mu_0 I\]
より
\[B=\frac{\mu_0}{2\pi}\frac{I}{R}\]
で(3)式と同じ結果を得る。簡単すぎるので(3)式の導出の方が何やら高級な感じがするが!
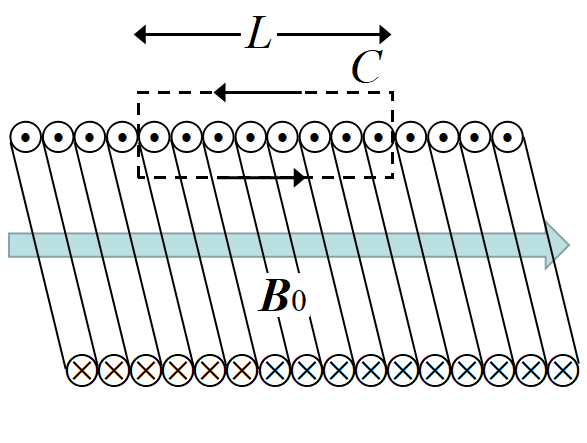
ソレノイドの作る磁場
磁場はソレノイドの内部のみだから, 四角の曲線\(~C~\)に沿った線積分は, \(B_0 L\)である。
長さ\(~L~\)のソレノイドの巻き数を\(~N~\)とすると, 全電流は\(~NI~\)だから
\[B_0 L=\mu_0 NI\]
単位長さ当たりのソレノイドの巻き数を\(~n~\)とすると\(~n=N/L~\)より
\[B_0=\mu_0 nI\]
となる。ビオ・サバールの方法で計算出来なくもないが, かなり面倒である。
電磁場の相対性
この項は殆どファインマン物理IIIのままである。然し原著では誤解を招きやすい表現や, 余りに多くの似通った記号が使われていて, 筆者も少なからず困惑した。そこで厳密さは欠くが, 理解しやすい表現に改めた。原著者, 訳者にはお詫び申し上げる。
さて高校物理では次の様に習った。
真空中で互いに\(~R[m]~\)離れて平行に置かれた2つの導線に, 同じ向きに\(~I[A]\)の等しい電流が流す。導線には引き合う力が働き, その大きさ\(~F[N]\)は
\[F=\frac{\mu_0}{2\pi}\frac{I^2}{R}\]
である。一方の直線電流が他方の位置に(3)式の磁場\(\Vec B~\)を作り, もう一方の電流がその磁場から力を受ける, と解釈される。
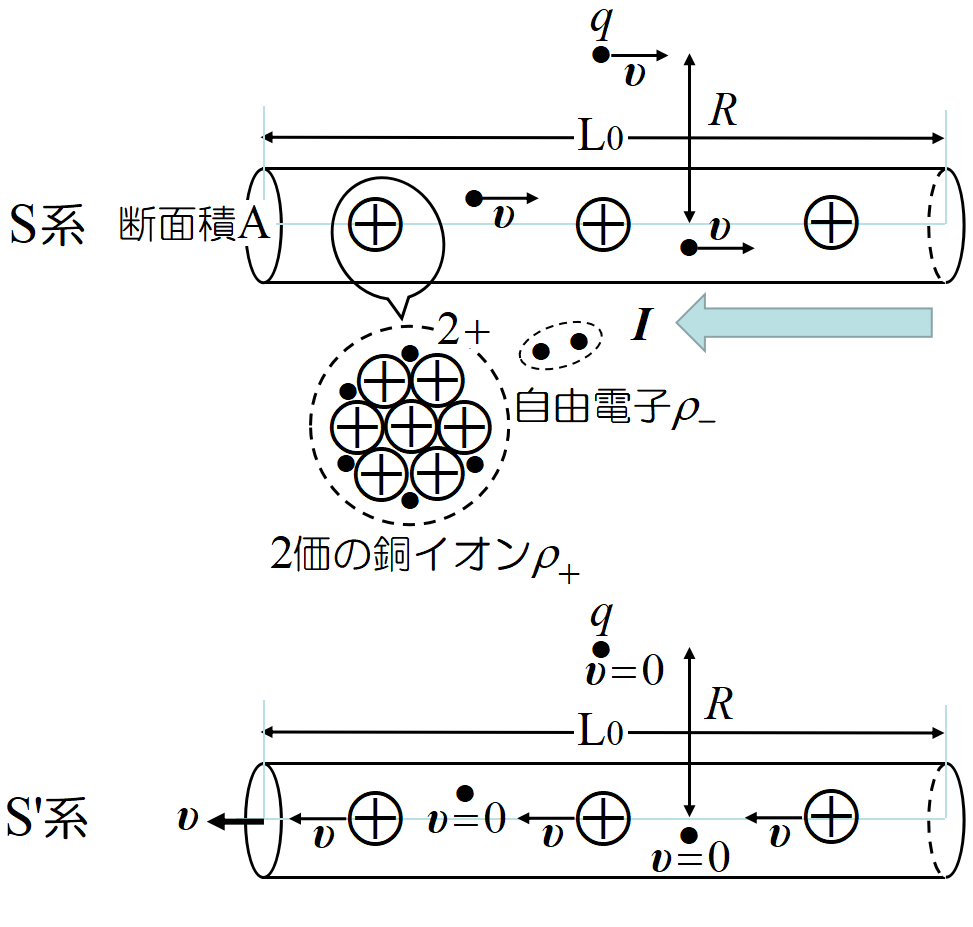
もう少し, ミクロの立場から眺めてみよう。固定した導線に電流\(~I~\)が流れており, 導線中の自由電子の速度を\(~\bm{\upsilon}~\)とする。もう一方の導線(図には書いていない)の中を同じ速度\(~\bm{\upsilon}~\)で粒子(電子)が右向きに運動しているとする。図にはこの粒子のみが書かれている。導線を固定した座標系を\(~S~\)系とする。
原子番号29の銅は, 通常2個の自由電子を持ち, 29個の固定した陽子と, 27個の固定した電子からなる原子である。+2価のイオンと2個の自由電子から構成されていると言っても良い。自由電子の密度を\(~\rho_-~\), イオンの密度を\(~\rho_+\)とすると, 明らかに\(~\rho_-=\rho_+\)。導線の断面積を\(~A~\)とすると, 電流は
\[I=\rho_- A\upsilon\]
である。
この電流が導線から距離\(~R~\)の所に作る磁場は, 式(3)から
\[B=\frac{\mu_0}{2\pi}\frac{I}{R}\]
である。この磁場と粒子(荷電粒子)の運動によってローレンツ力が発生し, 粒子は導線に引き寄せられる。大きさは
\[\begin{align}
F&=q\upsilon B \\
&=q\upsilon\frac{\mu_0}{2\pi}\frac{I}{R}\\
&=\frac{q\mu_0}{2\pi}\frac{\rho_- A\upsilon^2}{R} (\gets \varepsilon_0\mu_0=\frac{1}{c^2})\\
&=\frac{q}{2\pi\varepsilon_0}\frac{\rho_- A}{R}\frac{\upsilon^2}{c^2}\tag{9}\\
\end{align}\]
である。ここで視点を変え, 粒子を固定し, 導線を速さ\(~\upsilon~\)で左向きに動かす。
この系を\(~S'~\)系とする。\(~S'~\)系のパラメーターには全て('ダッシュ)を付ける。
導線と一緒に走る正電荷(2価のイオン)は粒子の位置に磁場\(~B'~\)を作る。しかし粒子は静止しているので, ローレンツ力は働かない。導線中の電子は粒子に対して静止しているから, 当然何の働きもしない。
では粒子を引き付ける力はどこから生み出されるのであろうか?
ローレンツ(フィッツジェラルド)収縮
特殊相対性理論の教えるところによれば, 速度\(~\upsilon~\)で運動する物体は, 自身の静止系で測定される長さである固有長よりも短く測定される。
導線は粒子から見ると長さが短縮して見え,
\[L'=L_0\sqrt{1-(\upsilon/c)^2}\]
となる。長さが短くなるのだから密度は増加し, イオンの密度は
\[\rho_+\,'=\rho_+ \frac{1}{\sqrt{1-(\upsilon/c)^2}}\]
と増加する。一方自由電子は速度が\(~\upsilon \to 0~\)となるので密度は減少し
\[\rho_-\,'=\rho_-\sqrt{1-(\upsilon/c)^2}\]
となるが, 負電荷の減少は正電荷の増加と同じだから,
\[
\rho\,'=\rho_+ \frac{1}{\sqrt{1-(\upsilon/c)^2}}+\rho_-\sqrt{1-(\upsilon/c)^2}
\]
ここで\(~\rho_-=\rho_+~\)だから
\[\rho\,'=\rho_+ \frac{(\upsilon/c)^2}{\sqrt{1-(\upsilon/c)^2}}\]
すなわち導線は正に帯電していて, 外部に静止している粒子の場所に電場\(~E~\)を作る。
一様に帯電した円筒の静電気問題の解は周知で,
\[E\,'=\frac{\rho\,'A}{2\pi\varepsilon_0 R}=\frac{\rho_+ A (\upsilon/c)^2}{2\pi\varepsilon_0 R\sqrt{1-(\upsilon/c)^2}} \]
であり, 外部の粒子はこの電場により
\[F'=\frac{q}{2\pi\varepsilon_0}\frac{\rho_+ A}{R}\frac{\upsilon^2}{c^2}\frac{1}{\sqrt{1-(\upsilon/c)^2}}\tag{10}\]
のクーロン力を受ける。(9)式と比べると, 因子\(\displaystyle \frac{1}{\sqrt{1-(\upsilon/c)^2}}\simeq 1+\frac{1}{2}(\upsilon/c)^2 \)を無視すれば一致している。
このように電場と磁場は見る立場によって互いに入り混じって姿を変える。
上述の逆を考えて再び\(~S~\)系に戻せば, 電場が消えて磁場が現れ, ローレンツ力*が見えるようになる。(*この部分だけは筆者の独断)
これが電磁場の本質で, 磁気的な現象は電場の相対論的な補正項の効果であるとも言える。
驚くべきはその補正の小ささで, \(~10^{-25}\) 程度である。次はファインマン電磁気学IIIの一節(12ページ)である。
「電線中の電子の速度を評価してみると, 電線にそった平均速度はだいたい\(~0.01cm/sec~\)である。従って\(~\upsilon^2/c^2~\)は\(~10^{-25}\)くらいになる。確かに無視できる"補正" である。しかしとんでもない!このばあい、磁気力は動く電子間の"普通"の電気力に比べると\(~10^{-25}\) 倍であるが, 電線には同数の陽子と電子があるためほとんど完全に打ち消し合って, "普通"の電気は消滅していることを忘れてはならない。打ち消しは\(~10^{-25}\)よりも精密で、そのため磁場と呼ぶ小さな補正だけが残る。それが主要な項になる。
物理学者が実際は相対論的効果であることを知らなくても, 相対論的効果(磁場)が研究でき\(~\upsilon^2/c^2~\)の程度まで正しい方程式を発見できたのは電気力の打ち消し方がこうも完全であったためである。そして同じ理由で, 相対論が発見されたときにも, 電磁気の法則は変更する必要がなかった。力学とちがって, 電磁気の法則は\(~\upsilon^2/c^2~\)の精度で正しい 」
極性ベクトルと軸性ベクトル
ファインマン電磁気学III, 13-8 (172ページ)は
極性ベクトルと軸性ベクトルの説明である。
軸性ベクトル
座標系の成分全ての符号を逆転させる変換を空間反転と呼ぶ。この時ベクトルの向きも一緒に変わってしまうものを軸性ベクトルと言う。座標系の取り方に応じてベクトルの向きも変わってしまうということは,座標系からの見え方, すなわちベクトルの成分は変わらない。
軸性ベクトルの向きは, 物理的にその向きに何か実体があるのではなく, 計算の便宜のために座標系に従って決められたものである。従って観測者と一緒にベクトルも動き, 観測者からの見え方は変わらないので都合の良いことが多い。力のモーメント, 角速度, 磁束密度などは軸性ベクトルである。実体は無いので, 数学者は擬ベクトルと呼ぶ事が多い。
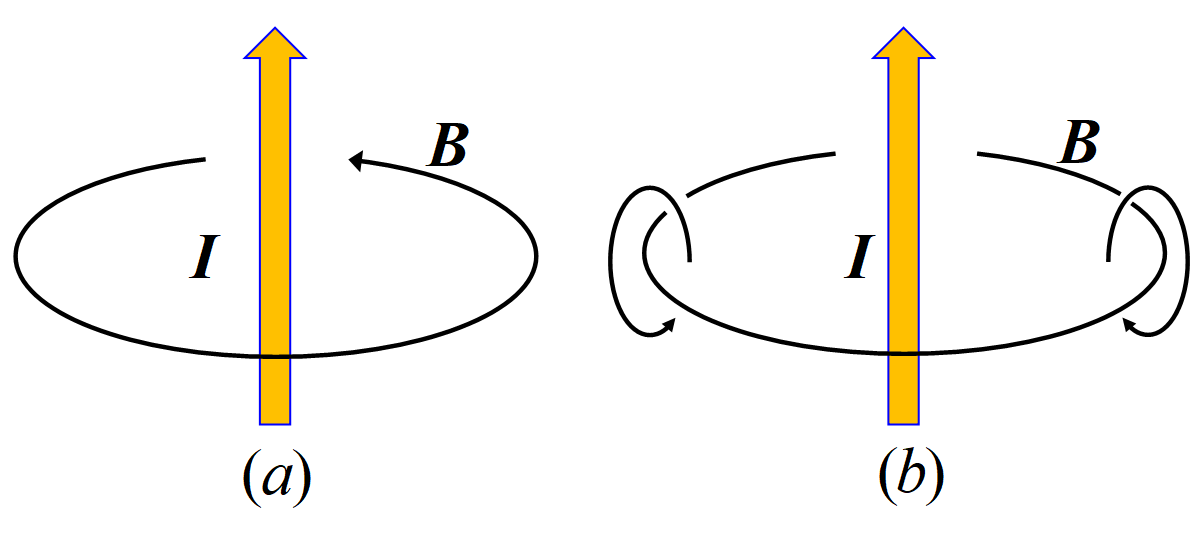
意外であるが, 磁場\(~\Vec B~\)も軸性ベクトルである。磁場\(~\Vec B~\)は微分オペレータ∇(ナブラ)とベクトルポテンシャル\(~\Vec A~\)との外積で,
\[\Vec B=\nabla\x \Vec A\]
で与えられる。外積の計算ルールに従い, 軸性ベクトルである。見慣れている(a)ではなく, (b)が正しいイメージである。(中田陽介 極性ベクトルと軸性ベクトル)
極性ベクトル
それに対し,空間反転をしても向きを変えないベクトルを極性ベクトルと呼ぶ。極性ベクトルは, 力, 速度, 位置など物理的に実体のあるベクトルである。座標系の向きを変えてもベクトル本体の向きは変わらないから, 観測者から見た見え方, つまりベクトルの成分は座標変換に応じて変わる。