\(Maxwell~\)方程式は, 2004年\(~Physics\,World~\) 誌での読者調査で, オイラーの等式\(~e^{i\theta}+1=0~\)と並び,「史上最も偉大な方程式」\(~(Greatest\,equation\,ever)~\) に選ばれた。電磁気学の定式化は, 1845年早くもガウスによって試みられ, 1858年, 弟子の B.リーマンは電磁場の伝搬が光の速度に関係することを示唆する波動方程式を得ている。マックスウェルは, それまで一貫性の無かった理論をファラデーの考えを道標(みちしるべ)とし, 苦労して20本の方程式に書きなおした。そして1865年「電磁場の動力学」を出版した。
20本の方程式を現代の我々が知る4本の方程式にまとめたのは, ヘビサイド, およびヘルツである。ベクトルポテンシャルを捨て去った等はあるが, 多くの人々が, 難解な\(Maxwell~\)方程式を理解できるようになったのは, この二人に負うところが大きい。
マックスウェル・アンペールの法則 \(Maxwell~\)方程式の中で唯一の理論式
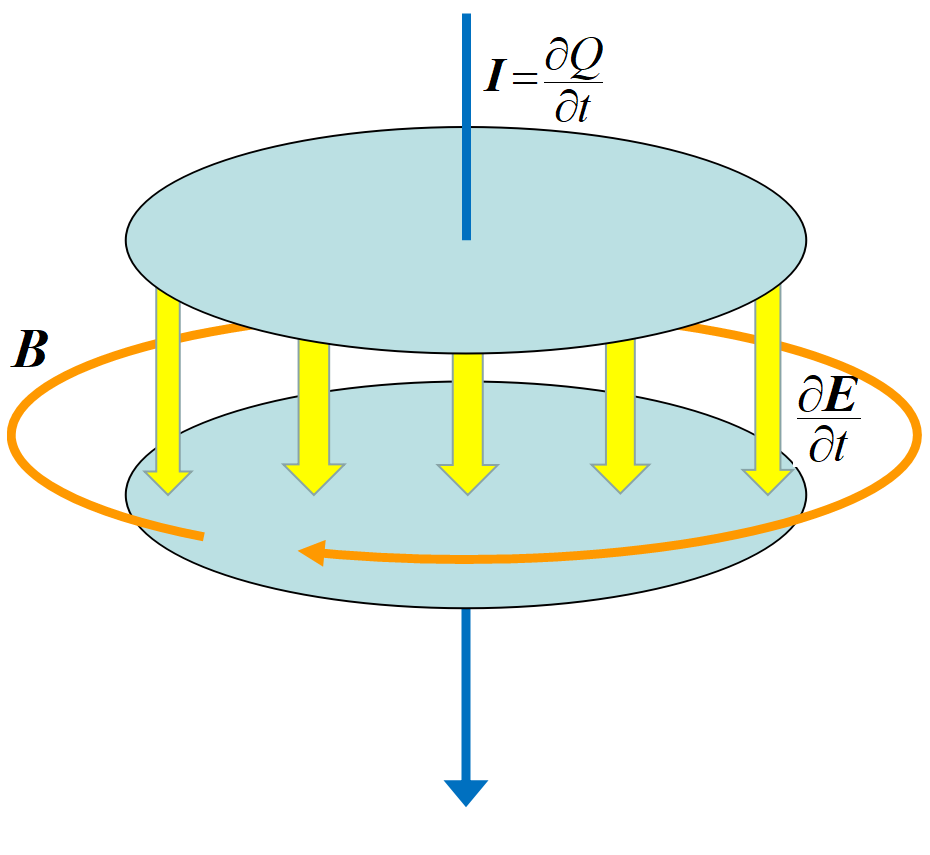
変位電流 電気工学では交流電流はコンデンサーを流れるというが。
図は平行平板コンデンサで, 導線部は金属導体中の電子が移動して交流電流が流れ(伝導電流), その周りにはループ状の磁場が発生する。極板の間は空間だから電子の移動はなく, 電流は流れない。そうすると磁界がコンデンサの部分だけとぎれていることになり不自然である。そこでマクスウェルは, 極板間の変動している電界の周りにも, 電流と同じように磁場が発生するとした。
マックスウェル・アンペールの法則
ベクトル解析に長じていたマックスウェルは, アンペールの法則
\[\nabla\x \Vec B=\mu_0\bm{j}\tag{1}\]
がどこかおかしいと気が付いた。両辺の\(~div~\)を取ると\(~div\,rot~\)は必ず\(~0~\)だから, 左辺は\(~0~\)。すると右辺の電流密度\(~\bm{j}~\)の\(~div~\)も\(~0~\)になる。
空間は定常電流だけで電荷はゼロということになる。通常, 真空以外は閉曲面内部に電荷が存在して, 内部の電荷の減少が電流となる。
\[\nabla\cdot \bm{j}=-\dd{\rho}{t}\tag{2}\]
は電流密度\(~\bm{j}~\)の定義でもある。
いわゆるマックスウェル・アンペールの式は
\[\nabla\x \Vec B=\mu_0\left(\bm{j}+\varepsilon_0\dd{\Vec E}{t}\right)\tag{3}\]
である。(1)式に(2)式をうまく取り込めないか?
物理的にも教育的にも無意味だが, 式変形だけでもできる。
(ファインマン電磁気p230~p231を逆に辿っただけであるが)やってみよう。(2)式を
\[\begin{align}
\nabla\cdot\bm{j}+\dd{\rho}{t}
&=\nabla\cdot\bm{j}+\varepsilon_0\dd{}{t}\frac{\rho}{\varepsilon_0}\\
&=\nabla\cdot\bm{j}+\varepsilon_0\dd{}{t}\nabla\cdot\Vec E\quad\left(\gets\nabla\cdot\Vec E=\frac{\rho}{\varepsilon_0}\right)\\
&=\nabla\cdot\left(\bm{j}+\varepsilon_0\dd{\Vec E}{t}\right)\\
\end{align}\]
と変形し, (1)式の\(~\bm{j}~\)の代わりに
\[\bm{j}\to\bm{j}+\varepsilon_0\dd{\Vec E}{t}\]
とすれば良さそうである。こうして(3)式が得られた。マックスウェルは, こんな安易な方法で導入した分けでは無いが, 意味を考えてみよう。
(3)式のカッコの中の第二項は何を意味するのであろうか?ガウスの法則は\(~E=Q/\varepsilon_0S~\)である。
\(Q/S=\varepsilon_0 E~\)は表面の電荷密度だから, 第二項\(~\partial(\varepsilon_0 E)/\partial t~\)は電荷密度の時間変化を表している。電荷の流れではないが, 電荷密度が時間的に変化することによって電流と同じ働きをすることから
変位電流と呼ばれている。
あるいは(3)式より, \(~\partial \Vec E/\partial t~\)も磁場を誘導するので, 「電流が磁場を誘導する」に倣って「変位電流」と呼ぶのかもしれない。
マックスウェルが辿った道は分からないが, 付加項\(~\partial \Vec E/\partial t~\)の素晴らしい働きに触れておこう。ファインマン物理III. p232からの引用である。
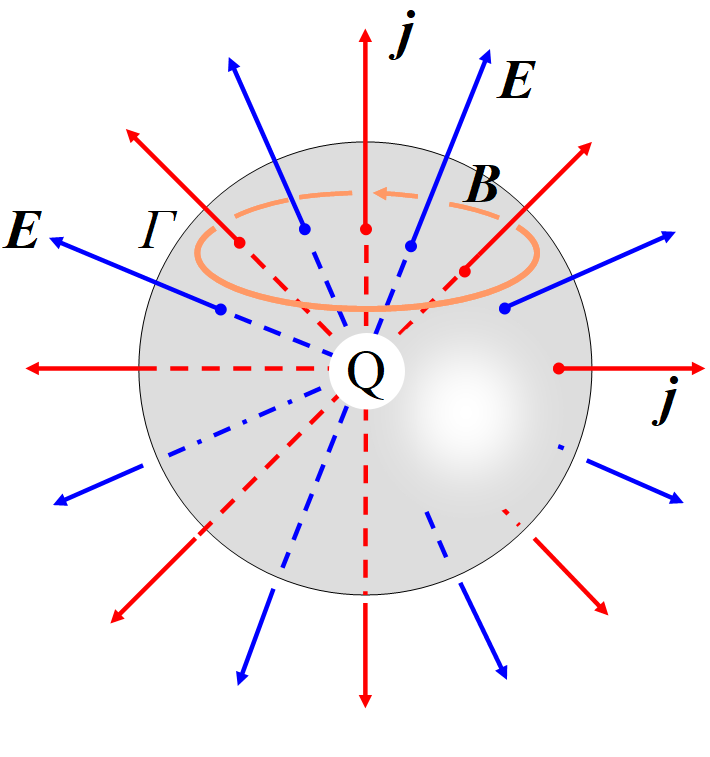
中心に電荷\(~Q~\)がある球対称な空間を考える。この電荷が崩壊して少しづつ外部へ流れる, すなわち放射状の電流があるとする。
半径\(~r~\)の内部にある全電荷を\(~Q(r)~\)とし, 同じ半径のところ(半径\(~r~\)の球表面)の\(~r~\)方向の電流密度を\(~j(r)~\)とする。電荷保存則から
\[\dd{Q(r)}{t}=-4\pi r^2 j(r)\]
である。するとこの電流が磁場を作るはずである。
半径\(~r~\)の球面上にループ\(~\Gamma~\)を書くと, このループを貫く電流があるから, 図の向きに回る磁場があるはずである。
しかしこれは明らかに変だ。電流は球対称であり, 特定の向きの磁場はありえない。
ループ\(~\Gamma~\)では電流だけではなく, \(\Gamma~\) を貫く電場
\(\displaystyle E=\frac{Q(r)}{4\pi \varepsilon_0 r^2}~\)も影響するはずである。
\[\dd{E}{t}=\frac{1}{4\pi \varepsilon_0 r^2}\dd{Q}{t}\]
に\(~\displaystyle \dd{Q(r)}{t}=-4\pi r^2 j(r)~\)を代入すると\(~\displaystyle \dd{E}{t}=-\frac{j}{\varepsilon_0}~\)を得る。これをマックスウェル・アンペールの式に適用すると
\[\begin{align}
\nabla\x \Vec B
&=\mu_0\left(\bm{j}+\varepsilon_0\dd{\Vec E}{t} \right) \\
&=\mu_0 \left(\bm{j}+\varepsilon_0\left(-\frac{\bm{j}}
{\varepsilon_0}\right)\right) \\
&=0
\end{align}\]
となって磁場\(~B~\)が消えてしまう。手品のようであるが, これは変位電流がこじつけでは無く, 正しく物理現象を表していることの証拠である。
電場・磁場の波動方程式 マックスウェル方程式のハイライト\(~No.1~\)
さあこれで\(~Maxwell~\)方程式が出揃った。
\[\begin{align}
\text{I}&.\quad\nabla\cdot\Vec E=\frac{\rho}{\varepsilon_0} \qquad
\text{II}.\quad\nabla\x \Vec E=-\dd{\Vec B}{t} \\
\text{III}&.\quad\nabla\cdot\Vec B=0 \qquad\;\;
\text{IV}.\quad\nabla\x \Vec B=\mu_0\left(\bm{j}+\varepsilon_0\dd{\Vec E}{t}\right)
\end{align}\]
電場・磁場の波動方程式
水中の光の速度は\(~\upsilon=c/n~\)である。これを導いたところで感動は薄れる。真空中の電磁波の速度\(~c~\)を導こう。
真空中のファラデーの法則, マックスウェル・アンペールの法則は
\[\begin{align}
rot\Vec E&=-\dd{\Vec B}{t} \tag{4}\\
rot\Vec B&=\frac{1}{\upsilon^2}\dd{\Vec E}{t}\tag{5}
\end{align}\]
である。この2つの式から波動方程式を導出するので,
\(\varepsilon_0\mu_0=1/\upsilon^2~\)と置きかえた。
(4)式の両辺の\(~rot~\)を取る。
\[rot\,rot\Vec E=-\dd{}{t}(rot\Vec B)\]
左辺を公式\(~rot\,rot\Vec X=grad\,div\Vec X-\triangle\Vec X\)で, 右辺を(5)式で置き換えると
\[grad\,div\Vec E-\triangle\Vec E=-\frac{1}{\upsilon^2}\dd{}{t}\left(\dd{\Vec E}{t}\right) \]
真空中なので\(~div\Vec E=0~\)だから左辺第1項は消えて
\[\left(\triangle-\frac{1}{\upsilon^2}\dd{^2}{t^2}\right)\Vec E=0 \tag{6}\]
これは速度\(~\upsilon~\)で進む波を表す波動方程式である。また(5)式の\(~rot~\)を取り, 途中\(~div\Vec B=0~\)を用いれば\(~\Vec B~\)に対する波動方程式
\[\left(\triangle-\frac{1}{\upsilon^2}\dd{^2}{t^2}\right)\Vec B=0 \tag{7}\]
が得られる。(6),(7)式をベクトル波動方程式と呼ぶ。
マックスウェルはこの速度, \(\upsilon=1/\sqrt{\varepsilon_0\mu_0}~\)が, 当時得られていた光の速度\(~c~\)と極めて近いので, 光は電磁波であると確信した。
後年アインシュタインが「この式に到達した時, マックスウェルの喜びは如何ばかりであったろうか」といった主旨の文を書いている。
実は心が躍ったのはアインシュタイン自身ではなかったのか?筆者も少なからずドキドキしたのを覚えている。
電磁場の性質(1) 縦波か横波か?
波には進行方向に垂直に振動する横波と, 進行方向に振動する縦波がある。
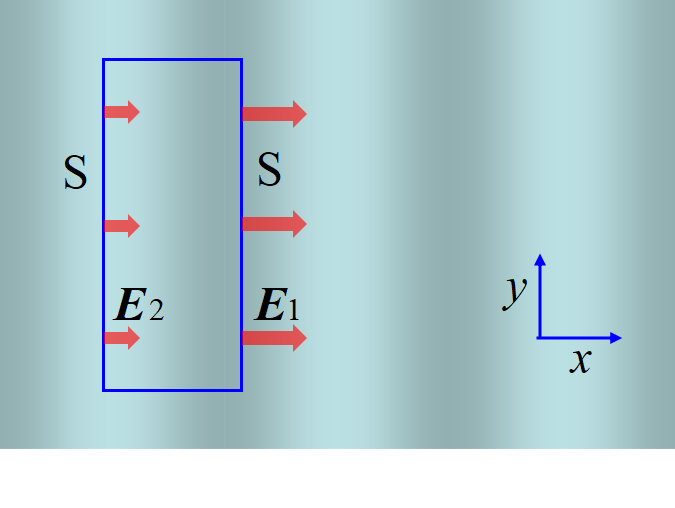
縦波は, 別名粗密波とも呼ぶ。電場が縦波であるとし, 密な部分の電場が大きいと仮定する。
図の(図面の手前から奥へ向かう)四角柱の左右の面の面積を\(~S~\)とし, ガウスの法則を適用する。
真空中の電荷は0だから,
\[\int_{S}\Vec E\cdot\,d\Vec S=S(E_1-E_2)=0 \]
とならなければならない。\(E_1\neq E_2~\)だからこれは矛盾である。つまり電場は縦波ではなく, 横波である。磁場も同様で, 電磁波は横波である。
電磁場の性質(2) 電場と磁場の直交性。
ファラデーの法則
\[\nabla\x \Vec E=-\dd{\Vec B}{t}\]
で, ナブラ(∇)はベクトル演算子で
\[\nabla=\dd{}{x}\bm{i}+\dd{}{y}\bm{j}+\dd{}{x}\bm{k}\]
であった、
\(\nabla\x \Vec E~\)はベクトル積(外積)で, \(\nabla~\)にも\(~\Vec E~\)にも垂直である。
\(\nabla~\)がどの方向を向いているかは分からないが, \(\nabla\x \Vec E~\)は, 時間変化する磁場\(~\partial \Vec B/\partial t~\)と垂直である。
磁場\(~\Vec B~\)は時間変化しても向きは変わらないだろうから, 結局, 電場は磁場に垂直である。
ここで述べている「向き」は「波の進行方向」ではなく, 進行方向に垂直な面内での「場の変位の方向」である。
マックスウェル・アンペールの法則を用いても同じ結果を得る。
波動の一般論 波数ベクトルに慣れよう!
進行波と後退波 先ずは高校物理の復習。
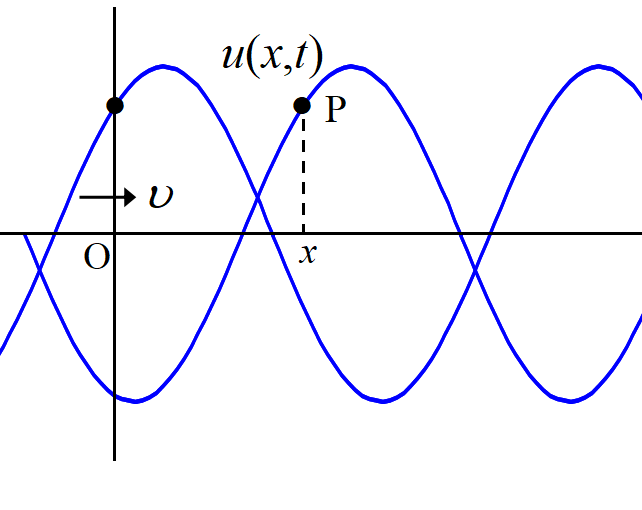
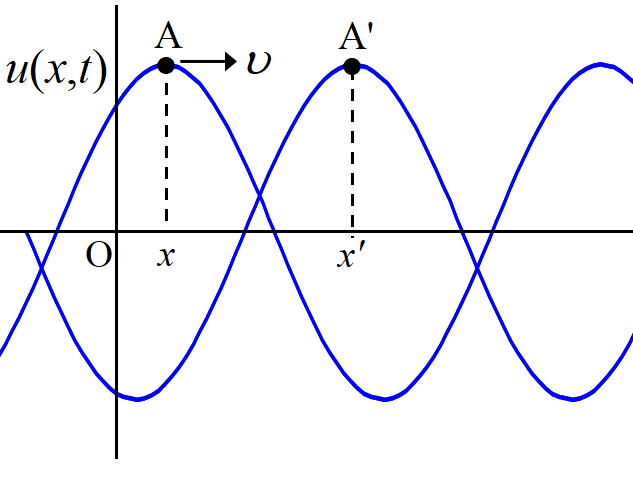
原点 O 上の媒質の変位を
\[u(0,t)=Asin(\omega t+\phi)\]
とし, この変位が速度\(~\upsilon~\)で\(~x~\)軸の正の方向に伝わってゆくとする。
原点からの距離\(~x~\)の地点 P の時刻\(~t~\)における変位を\(~u(x,t)~\)とする。
同時刻に点 O も変位しているが, 点 P と同じではない。点 P の変位は, 時刻\(~t-\triangle t~\)の点 O の変位が遅れてやって来る。
つまり\(~\triangle t~\)秒前の点 O の変位\(~u(0,t-\triangle t)~\)が点 P の時刻\(~t~\)における変位である。
\(\triangle t=x/\upsilon~\)であるから, 点 P の時刻\(~t~\)における変位は
\[\begin{align}
u(0,t)
&=u(0,t-\triangle t)\\
&=u\left(0,t-\frac{x}{\upsilon}\right)\\
&=Asin\left(\omega\left(t-\frac{x}{\upsilon}\right)+\phi \right)\\
&=Asin\left(\omega t-\frac{\omega}{\upsilon}x +\phi \right)\\
&=Asin(\omega t-kx+\phi)\tag{8}\\
\end{align}\]
途中\(~\omega/\upsilon=2\pi f/f\lambda=2\pi/\lambda=k~\)を用いた。
\(k~\)を波数と呼び, 長さ\(~2\pi\,[m]~\)の中に, 波が何波長入っているかを表しているものである。
高校物理では出てこないが今後頻出するので慣れておこう。
(8)式をさらに変形して
\[\begin{align}
u(0,t)
&=Asin(\omega t-kx+\phi)\\
&=Asin \left(k\left(\frac{\omega}{k}t-x\right)+\phi\right)\\
&=Asin k(\upsilon t-x +\phi') \tag{9}
\end{align}\]
とすることも多い。
高校物理では正弦波を表す式として
\[y=Asin2\pi\left(\frac{t}{T}-\frac{x}{\lambda}\right)\]
を習った。\(k=2\pi/\lambda,\,\omega=2\pi/T~\)を使えば(8)式と同じである。
初期位相だけの問題なので, (8), (9)式は\(~u=f(kx-\omega t)~\), \(~u=f(x-\upsilon t)~\)と書いても良く, こちらが一般的に用いられているようである。
(9)式の関数\(~u=f(x-\upsilon t)~\)は, \(t=0,\,x=0~\)で持っていた波形\(~u=f(0)~\)を\(~t~\)秒後は\(~x=\upsilon t~\)の場所で保持する。
すなわちこの関数は速度\(~\upsilon~\)で進行する波を表す。同様に関数\(~u=g(x+\upsilon t)~\)は逆方向に進む波を表す。
このような説明が多いが, 分かりにくい読者もいると思うので, 別の例も挙げておく。
変位を\(~u(x,t)=Asin(kx-\omega t)~\)とする。
時刻が\(~t \to t+\triangle t~\)と変化すると, 変位\(~u(x,t)~\)は
\[u(x',t+\triangle t)=Asin\{\omega(t+\triangle t)-kx'\}\]
となる。\(u(x,t)=A~\)(振幅)となる点に着目する。
\[\omega t-kx=\frac{\pi}{2}\dots(1)\qquad\omega (t+\triangle t)-kx'=\frac{\pi}{2}\dots(2)\]
\((1)-(2)~\)から, \(k(x'-x)-\omega\triangle t=0~\)。
\[\upsilon=\frac{x'-x}{\triangle t}=\frac{\omega}{k}=f\lambda\]
となって, 確かに速度\(~\upsilon~\)で進む波を表している。
当記事では原則として進行波を
\[u(x,t)=Asin(kx-\omega t)\quad or \quad u(x,t)=f(x-\upsilon t)\tag{10}\]
後退波を
\[u(x,t)=Asin(kx+\omega t)\quad or \quad u(x,t)=f(x+\upsilon t)\tag{11}\]
と表すこととする。
ここで一つ注意すべき点を挙げておく。
\(kx-\omega t~\)は三角関数(または指数関数)の変数である。任意の波形に対しては\(~x-\upsilon t~\)の方が良さそうであるが, それは違う。
任意の(周期)関数は, 三角関数によるフーリエ級数で展開できるので, 波動現象の本質解明は, 正弦波動関数の持つ性質を理解することの方が基本である。
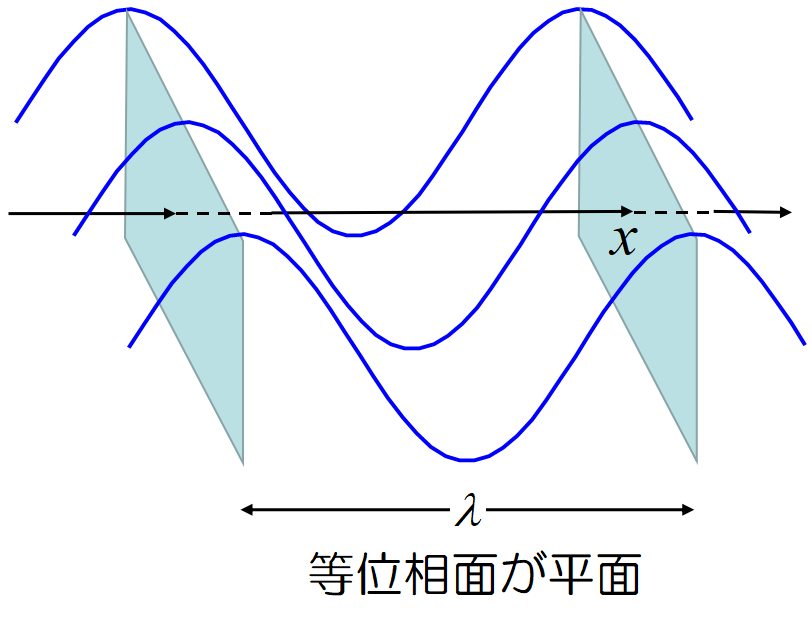
平面波 波数ベクトル\(~\bm{k}~\)の導入。
平面波とは位相の等しい面が平面になっている波のことである。
上述(10)式の関数\(~u(x,t)=Asin(kx-\omega t)~\)は, \(~x=\)一定の所で位相が等しい(同時刻\(~t~\)で同じ値を取る)ので, 平面波であり, \(x~\)方向に進む波を表す。
ここで, 座標\(~y,\,z~\)はどう取り扱えば良いのかを疑問に思われる読者もいると思う。今考えているのは横波であるから(実は縦波でも良いのだが, 今は理解しやすいように考える), 変位は\(~x~\)軸に垂直な面に限られる。そこで変位の方向に\(~y~\)軸もしく\(~z~\)軸を取れば良い。\(y~\)と\(~z~\)の中間45°の方向に変位するときは, \(~y~\)軸もしくは\(~z~\)軸をその方向に取り直せば良い。
今, 進行方向が\(~x~\)ではなく, 任意の方向を向いているときはどうすれば良いのであろうか?
座標系をどのように設定しようと物理現象は変わらないので, 座標系を回転して\(~x~\)軸を波の進行方向に取り直せば良い。
つまり\(~x~\)軸も\(~y~\)軸も\(~z~\)軸も, 都合の良い向きに設定すれば良いのである。
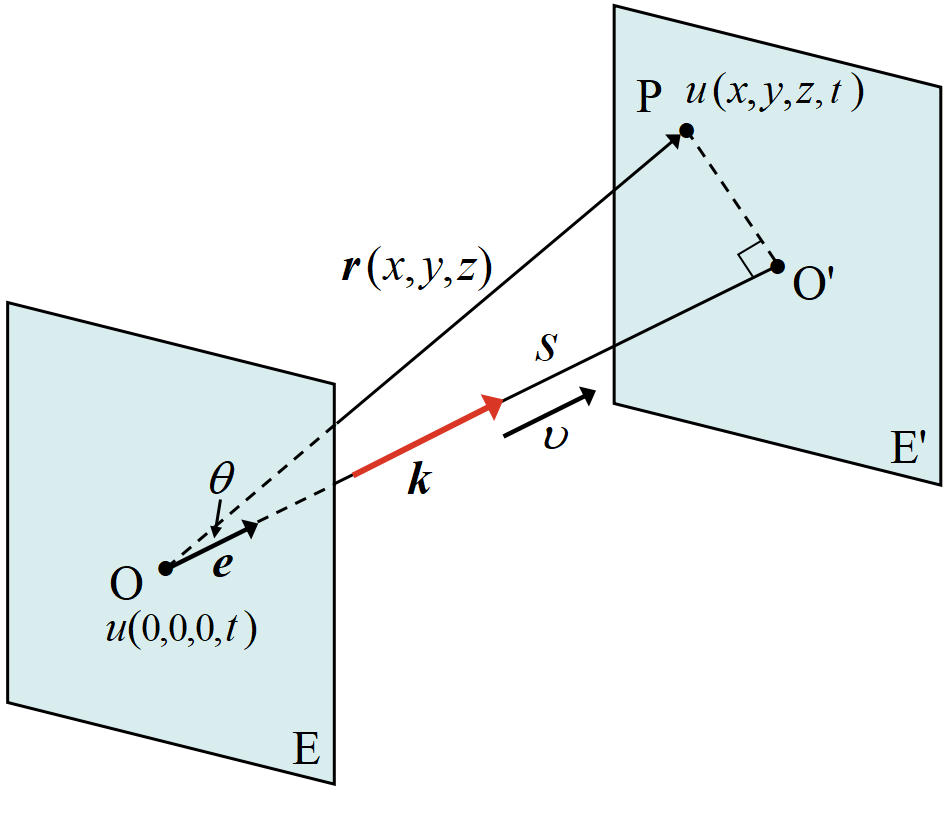
原点を含む波面\(~E~\)上の点 O\((0,0,0)~\)上の媒質の変位を
\[u(0,0,0,t)=Asin(\omega\,t +\phi)\]
とする。この波面が速度\(~\bm{\upsilon}~\)で動く。時刻\(~\triangle t~\)秒後の波面を\(~E'~\)とし, \(~E'~\)上の任意の点 P の変位\(~u(x,y,z,t)~\)を求めてみよう。
点 O の, 波面 E' 上への移り先を O' とする。点 P の変位と点 O'の変位は等しい(平面波の定義)。
今, 時刻\(~t~\)の点 P の変位, すなわち点 O' の変位を考える。同時刻に点 O も変位しているが, 点 O' と同じではない。
点 O' の変位は, 時刻\(~t-\triangle t~\)の点 O の変位が遅れてやって来る。
つまり\(~\triangle t~\)秒前の点 O の変位\(~u(0,0,0,t-\triangle t)~\)が点 O' の時刻\(~t~\)における変位である。
O から O' へ向かう単位ベクトルを\(~\bm{e}~\)とする。O~O' の距離\(~s~\)は, \(s=\bm{r}\cdot\bm{e}~\)だから\(~\triangle t~\)は
\[\triangle t=\frac{s}{\upsilon}=\frac{\bm{r}\cdot\bm{e}}{\upsilon}\]
これより
\[\begin{align}
u(x,y,z,t)
&=u(0,0,0,t-\triangle t)\\
&=u\left(0,0,0,t-\frac{\bm{r}\cdot\bm{e}}{\upsilon}\right)\\
&=Asin\left(\omega\left(t-\frac{\bm{r}\cdot\bm{e}}
{\upsilon}\right)+\phi \right)\\
&=Asin\left(\omega t-\left(\frac{\omega}
{\upsilon}\bm{e}\right)\cdot\bm{r}+\phi \right)\tag{12}\\
&=Asin(\omega t-\bm{k}\cdot\bm{r}+\phi)\tag{13}\\
\end{align}\]
(12)式から(13)式へ移る途中で
\[\frac{\omega}{\upsilon}=\frac{2\pi f}{f\lambda}=k \]
を用いた。\(k~\)は波数である。
\[\bm{k}=k\cdot\bm{e}\]
を波数ベクトルと呼び, 波の進行方向へ向かう大きさ\(~k~\)のベクトルである。
(13)式は(8)式の3次元への自然な拡張になっていることが分かる。
電磁場の波動 前置きが長くなった。電場と磁場の関係を改めて考えてみよう。
電場と磁場の関係
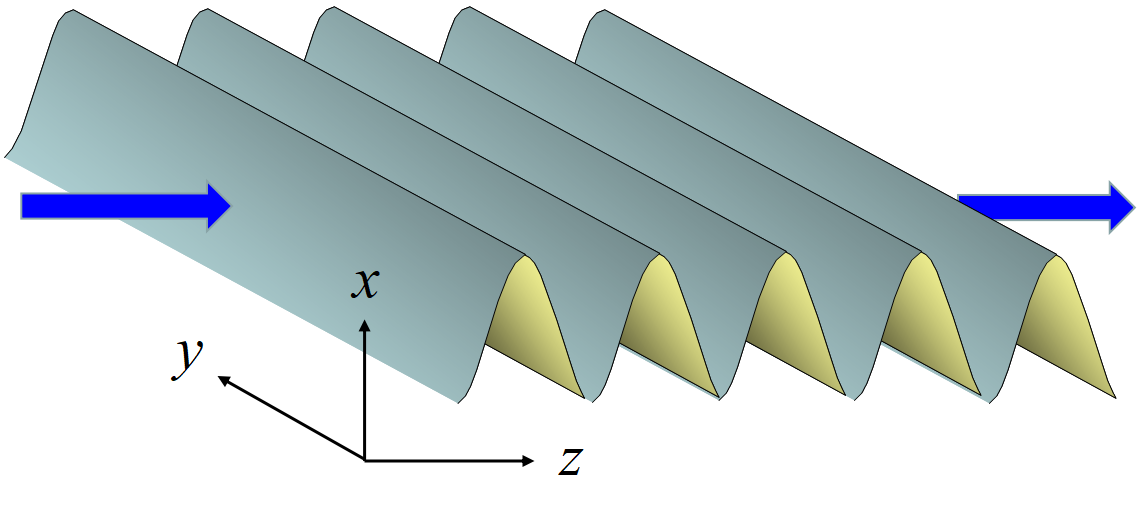
波の進行方向は特定の向きに取っても良いので, \(z~\)軸方向へ進む平面波を考える。横波であるから電場の変化は進行方向に垂直な面内のみなので, これを\(x~\)軸の方向に取ろう。すると
\[\begin{align}
E_x&=f(z-\upsilon t)+g(z-\upsilon t) \\
E_y&=0 \\
E_z&=0 \\
\end{align}\]
ファラデーの法則は
\[\nabla \x \Vec E+\dd{\Vec B}{t}=0\]
成分で表示すると
\[\begin{align}
\dd{E_z}{y}-\dd{E_y}{z}+\dd{B_x}{t}&=0 \\
\dd{E_x}{z}-\dd{E_z}{x}+\dd{B_y}{t}&=0 \\
\dd{E_y}{x}-\dd{E_x}{y}+\dd{B_z}{t}&=0
\end{align}\]
\(E_y=0,\,E_z=0~\)を代入すると,
\[\begin{align}
\dd{B_x}{t}&=0 \\
\dd{B_y}{t}&=-f'(z-ct)-g'(z+ct) \\
\dd{B_z}{t}&=0
\end{align}\]
2番目の式を\(~t~\)で積分すると
\[B_y=\frac{1}{c}f(z-ct)-\frac{1}{c}g(z+ct)\]
が得られる。これから
(1)磁場は\(~y~\)方向だけ, すなわち電場\(~E~\)と垂直な成分のみ。
(2)電場と磁場は定数である光速\(~c~\)だけの違いであることが分かる
この記事の前半の「\(\nabla\x \Vec E~\)は外積だから\(~\Vec E~\)と\(~\Vec B~\)は垂直である。」よりは納得できたであろうか。
波動方程式の一般解 話の順序が逆だが。
1次元の波動方程式は次の2階偏微分方程式で与えられる。
\[\dd{^2u}{x^2}-\frac{1}{\upsilon^2}\dd{^2u}{t^2}=0 \tag{14}\]
この解は, 微分可能な任意の2つの関数\(~f~\)と\(~g~\)を用いて
\[u=f(x-\upsilon t)+g(x+\upsilon t)\tag{15}\]
と表される。(15)式を実際に(14)式に代入して確かめるのが最も簡単だが
\[\dd{^2f}{x^2}=f'',\dd{^2f}{t^2}=f''\]
としてはいけないことを注意しておこう。もっとも, 強引にこうやっても出来てしまうのだが。
ここでは(14)式を因数分解する方法で(15)式の正しさを証明しよう。
(14)式を因数分解して良いのか?ということであるが, 今後もこの方法は用いられるので, その時びっくりしないように一回やってみよう。
(14)式は
\[\dd{^2u}{^x2}-\frac{1}{\upsilon^2}\dd{^2u}{t^2}
=\left(\dd{}{x}+\frac{1}{\upsilon}\dd{}{t}\right)
\left(\dd{}{x}-\frac{1}{\upsilon}\dd{}{t}\right)u \]
と因数分解できるので
\[\left(\dd{}{x}+\frac{1}{\upsilon}\dd{}{t}\right)u=0 \tag{16}\]
または
\[\left(\dd{}{x}-\frac{1}{\upsilon}\dd{}{t}\right)u=0 \tag{17}\]
である。(16)式の解は任意の関数\(~f\)(三角関数でなくとも良い)を用いて
\[u=f(x-\upsilon t)\tag{18}\]
と表せる。実際, \(\eta=x-\upsilon t~\)として\(~f(\eta)\)は
\[\dd{u}{x}=\dd{f}{\eta}\frac{d\eta}{dx}=f',\quad
\dd{u}{t}=\dd{f}{\eta}\frac{d\eta}{dt}=-\upsilon f' \]
で明らかに(16)式を満たす。同様にして(17)式の解は任意の関数\(~g~\)を用いて
\[u=g(x+\upsilon t)\tag{19}\]
と表せ, \(\tau=x+\upsilon t~\)として\(~g(\tau)~\)は
\[\dd{u}{x}=\dd{f}{\tau}\frac{d\tau}{dx}=f',\quad
\dd{u}{t}=\dd{f}{\tau}\frac{d\tau}{dt}=\upsilon f' \]
となり, これは(17)式を満たす。
こうして1次元の波動方程式(14)は, (18)式と(19)式の1次結合である(15)式が一般解となる。
一般的に, 2階の常微分方程式は2つの境界(初期)条件を与えれば解は一意的に定まり, 2階の偏微分方程式は2つの初期関数を与えれば解は一意的に定まる。