静電誘導と誘電分極は何が違う?
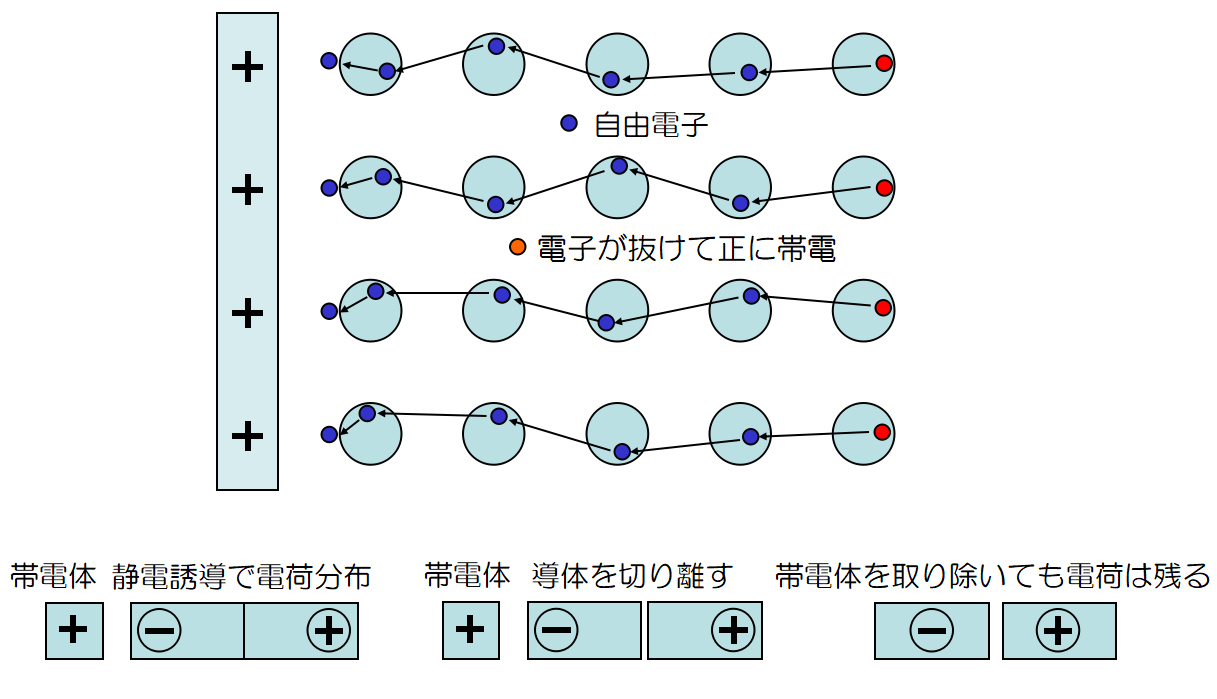
静電誘導 静電誘導は電子が実際に移動して電荷の偏りを生じる現象の事。
自由電子を持つ金属のような導体に帯電体を近づけると, クーロン力を受け自由電子が移動し, 導体の表面に電荷の分布を生じる。
電子が集まった方が負に, 電子が抜けた方が正に帯電する。この電荷を
誘導電荷と呼ぶ。
誘導電荷は帯電体の作る電場を弱め, 最終的には電子の移動は停止する。すなわち導体内部の電場はゼロ, 表現を変えれば導体内部は等電位となる。
電荷を分布させた後, 導体を切り離すと帯電体を取り除いても, 個々の導体に電荷が残る。
上図最後の状態で, 2つの金属片の間に働く力は?と時々入試問題に出題される。答えは「引力」である。
誘電分極
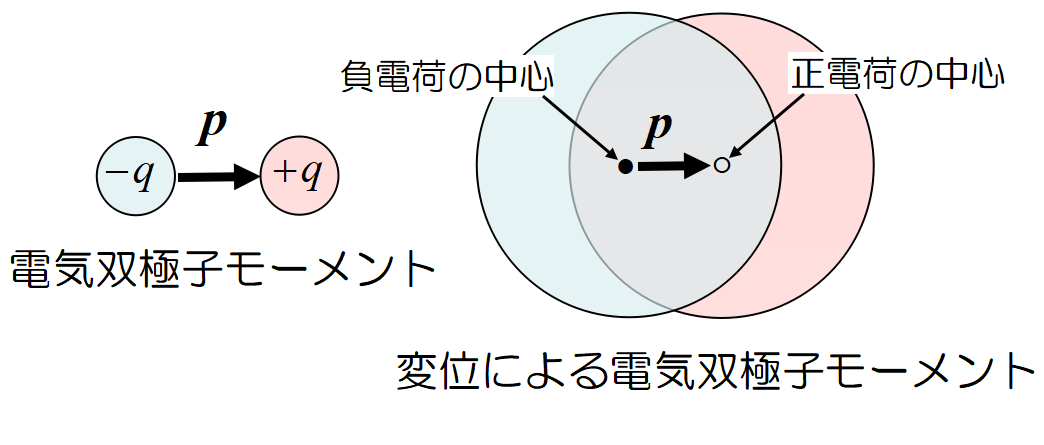
\(+q~\)と\(-q~\)の電荷があり, \(-q~\)から\(+q~\)へ向いたベクトルを\(~\bm{\delta}~\)とする。\(~d~\)をコンデンサーの極板間の距離に使うので\(~\bm{\delta}~\)を用いた。この時
\[\bm{p}=q\bm{\delta}\]
を電気双極子モーメントと呼ぶ。
電場中の原子, 分子, イオンには電荷の偏り(変位), 分極が生じてあたかも電気双極子のようになる。
分極\(~\Vec P~\)(単位体積あたりの電気双極子モーメント)は,\(~q\bm{\delta}\)を原子あたりの電気双極子モーメント, 単位体積あたりの原子数を\(~N~\)とすれば
\[\Vec P=Nq\bm{\delta} \tag{1}\ \]
である。注意すべきは\(~\Vec P~\)は分極の平均量で, マクロな量である。
分極の原因
分極の原因はいくつかある。ここでは名前だけを上げておく。名前から想像できるだろう。
(1) 電子分極:原子核(正電荷)と電子雲(負電荷)の中心がずれる。
(2) イオン分極:イオン結晶の陽イオンと陰イオンが変位する。
(3) 配向分極:水のような極性分子の双極子モーメントの向きが揃って出来る。
詳しくは上の用語で検索すれば容易に見出せる。
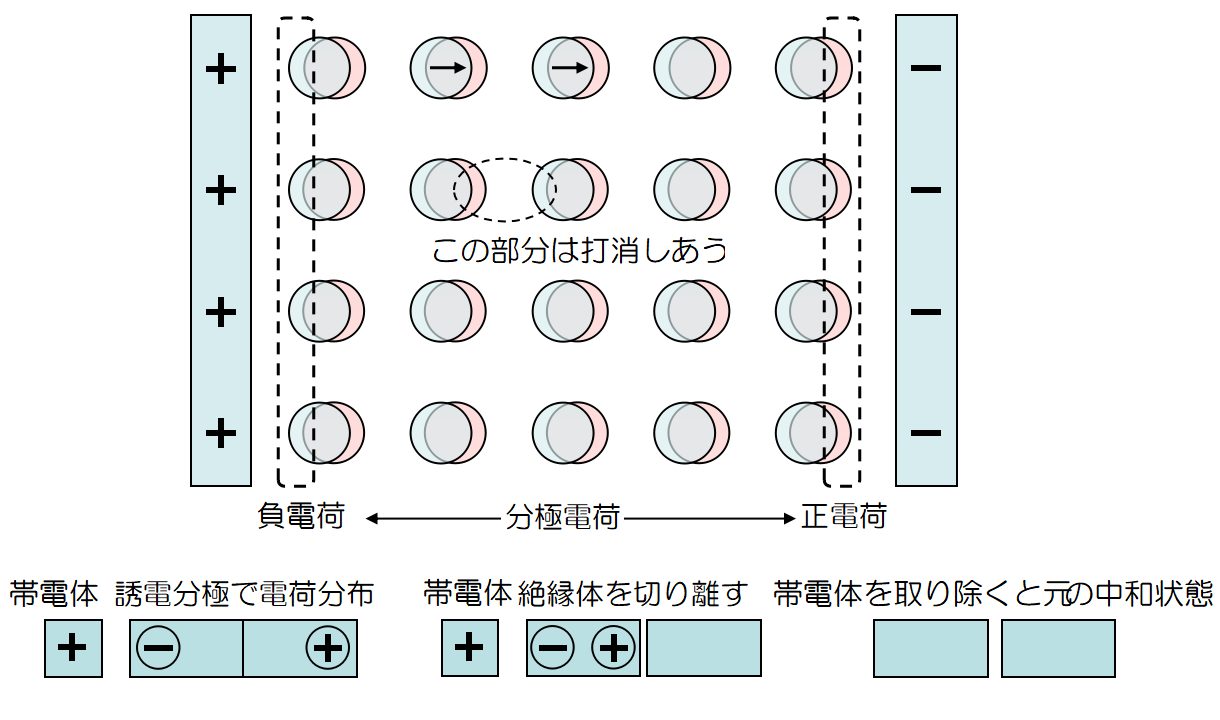
さて, 不導体に帯電体を近づける, 若しくは電場の中に置くと, 構成している原子や分子の電荷分布が変化し, 分子内の正電荷, 負電荷が同じ方向に並ぶ。この場合も導体と同じく不導体の表面に電荷の分布,
分極電荷を生じる。この現象が
誘電分極である。不導体を
誘電体とも呼ぶ所以でもある。
電荷を分布させた後, 不導体を切り離し帯電体を取り除く。すると, 原子や分子の電荷分布が元の中和状態に戻る。上図最後の状態で, 2つの不導体の間に働く力はゼロである。先ほどの金属とは随分と異なる。これも時々入試問題に出題される。
静電誘導と誘電分極比較
| | 電荷の偏りの原因 |
合成(内部)電場 | 内部電位 |
| 静電誘導 |
導体中の電子の移動 |
\(E-E'=0\) |
\(V=一定\) |
| 誘電分極 |
原子・分子の変位 |
\(E-E'\ge 0\) |
電位勾配\(~V~\)を持つ |
電束密度\(~\Vec D~\)と電場\(~\Vec E\)
コンデンサーの電気容量 高校物理の復習。
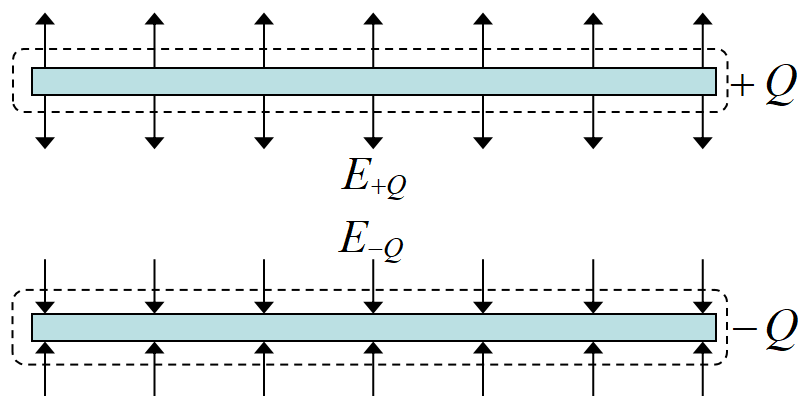
ガウスの法則で使った図をもう一度見てみよう。極板の面積を\(~S~\), 極板間の距離を\(~d~\)とする。
電場の大きさは\(\displaystyle E=E_{+Q} +E_{-Q} =\frac{Q}{\varepsilon_0 S}\)であった。極板間の電位差\(~V~\)は\(~V=Ed~\)だから
\[V=Ed=\frac{Q}{\varepsilon_0 S}d \]
より
\[Q=\frac{\varepsilon_0 S}{d}V \]
すなわち, コンデンサーに蓄えられる電荷は電位差に比例する。この比例定数を
\[C=\frac{\varepsilon_0 S}{d}\tag{2} \]
と書いて, 電気容量\(~C~\)と呼ぶ。
コンデンサーと誘電体 コンデンサーの極板間に誘電体を挿入すると, 電場が弱くなるという説明は多いが。
次の(1), (2)をはっきり区別しないので間違い易い。
(1)
充電後, 電源を切り離した状態で誘電体を挿入する場合 書籍,ネットではこちらの説明が多い。
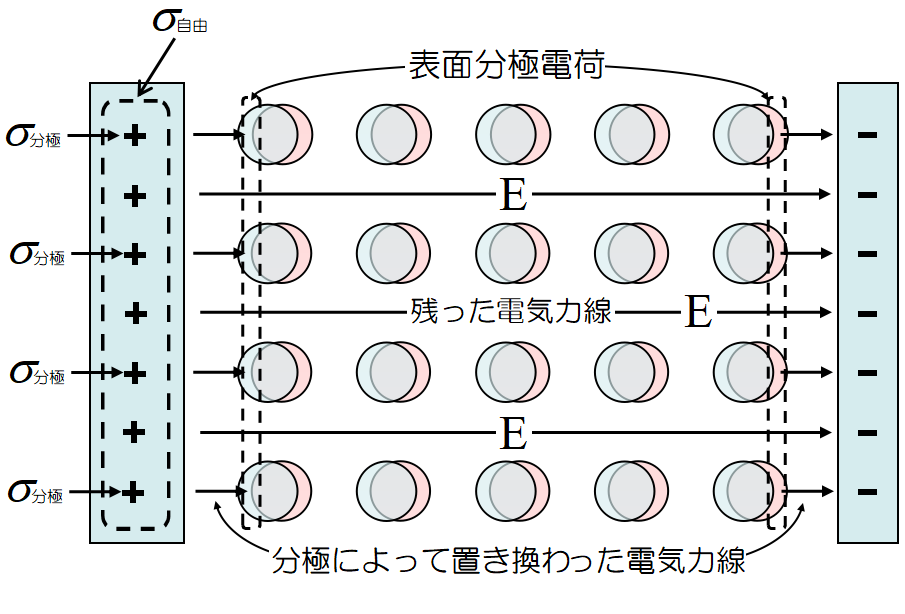
誘電体を挿入すると誘電体上に表面分極電荷が発生し, 極板上の電荷\(~\sigma_{分極}\)と釣り合う。
極板には新しく電荷は供給されないので, 元々あった電気力線は減少する。すなわち極板間, つまり誘電体内の電場は減少する。
電極上の電荷は自由に動けるので, その面密度を\(~\sigma_{自由}\)とし, ガウスの法則を適用する。単位面積で考えているから
\[E=\frac{\sigma_{自由}-\sigma_{分極}}{\varepsilon_0} \tag{3}\]
である。さて上図の表面分極電荷の面密度\(~\sigma_{分極}~\)は次の様に計算される。
\[\sigma_{分極}=Nq_e \delta \tag{4}\]
これは(1)式の分極ベクトル\(~\Vec P~\)の大きさ\(~P~\)に等しい。
分極\(~\Vec P~\)は単位体積当たりの電気双極子モーメントであった。単位体積とは言っているが, 体積内に平均的に分布するわけではなく, 一方の面のみに現われる。よって\(~\Vec P~\)と釣り合う極板上の(表面)分極電荷の面密度は\(~\Vec P~\)と等しくなる。
さて, 分極\(~\Vec P=Nq\bm{\delta}~\)で, \(\bm{\delta}~\)は電場\(~\Vec E~\)の大きさに
たぶん比例するだろうから
\[\Vec P=Nq\bm{\delta}=N\chi\varepsilon_0 \Vec E \tag{5} \]
と置く。この\(~\chi~\)を電気感受率, あるいは分極率と呼ぶ。
(後者は今はあまり用いられないようである。筆者のファインマンの教科書(邦訳第1刷1600円)では後者を使用)
(3)~(5)式から
\[E=\frac{\sigma_{自由}}{\varepsilon_0}\frac{1}{(1+\chi)} \tag{6}\]
すなわち, 場は\(~1/(1+\chi)~\)だけ弱くなる。\(\sigma_{自由}= Q\), \(~V= Ed~\)を用いて(6)式を書き直すと,
\[V=Ed=\frac{\sigma_{自由}}{\varepsilon_0 (1+\chi)}d=\frac{Q}{\varepsilon_0 (1+\chi)}d \]
より
\[Q=\frac{\varepsilon_0 (1+\chi)}{d} V \]
すなわち
\[C'= \frac{\varepsilon_0 (1+\chi)}{d}\]
となり, 誘電体を挿入した時の電気容量は\((1+\chi)\)だけ増加する。
(2)
電源を接続したまま誘電体を挿入する場合 こちらの説明は少ない。
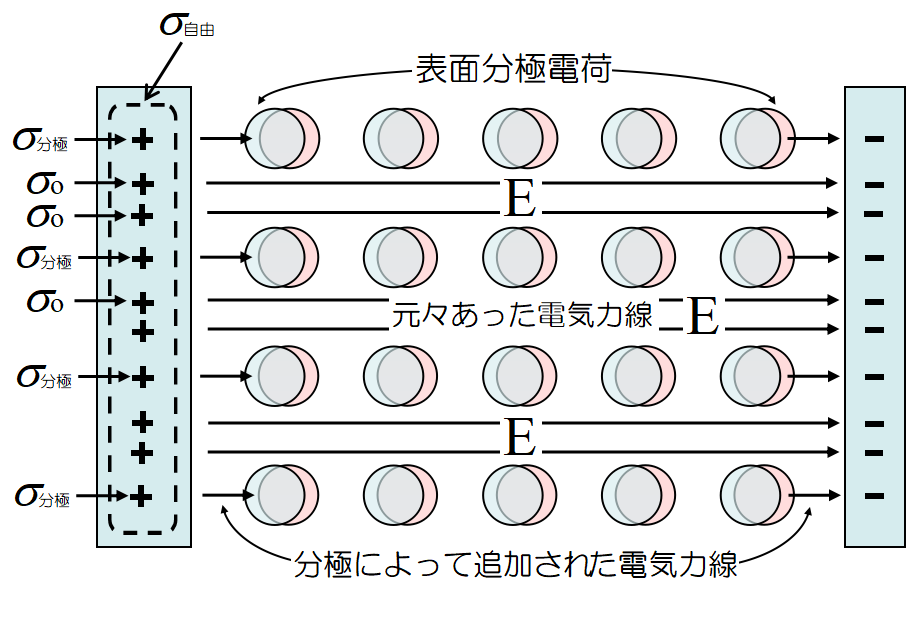
誘電体を挿入すると誘電体上に分極電荷が発生し, その分極電荷に対応する電荷\(~\sigma_{分極}~\)が新しく極板に供給される。
つまり同じ電圧\(~V~\)に対して, 極板の電荷が増大する。実用的なコンデンサーで強誘電体を使用する理由である。
コンデンサー内の電場を弱くするために誘電体を利用する訳ではない。もともとあった電気力線はそのまま存在しているので電場は変わらない。
誘電体挿入前の極板の電荷密度を\(~\sigma_o\), 極板上の増加した電荷密度を\(~\sigma_{分極} ~\) とすると,
\[\sigma_o=\varepsilon_0 E\]
\[\sigma_{分極}=P=\chi \varepsilon_0 E \]
極板の電荷密度は\(~\sigma_{極板}=\sigma_o+ \sigma_{分極}\)だから
\[\sigma_{極板}=\sigma_o+ \sigma_{分極}=\varepsilon_0 E+ \chi\varepsilon_0 E=\varepsilon_0(1+\chi)E=\varepsilon D\]
として, \(\Vec D~\)を電束密度と呼ぶ。\(\Vec D=\varepsilon_0 (1+\chi)\Vec E=\varepsilon \Vec E~\)だから\(~\Vec D~\)は,
\[\Vec D= \varepsilon_0 \Vec E+ \Vec P\tag{6}\]
または
\[\Vec D=\varepsilon \Vec E\tag{7}\]
と書かれる。\((1+\chi)~\)を比誘電率, \(\varepsilon=\varepsilon_0(1+\chi)~\)を誘電率と呼ぶ。
(6)式の意味は明快で, ベクトル云々はこの際目をつぶると両辺の単位は\(~[C]/m^2~\)。
真空時の電荷密度\(~\varepsilon_0 \Vec E~\)と, 誘電体を挿入した時分極によって増えた電荷密度\(~\Vec P~\)の和である。懸命に暗記するようなものでも無い。
(注:電束密度は, 正しくは不均一な\(~\Vec P~\)の発散から導くが, 分かり易くするために簡易的な方法にした。)
すなわち, 真空中のコンデンサー\(~\sigma_{真空}=\varepsilon_0 E~\)の代わりに,
\(\sigma_{誘電体}=\varepsilon D\)として考えれば良いということである。
実は単位体積で考えて, 電荷の体積密度を\(~\rho~\)とすれば, それぞれ
\[\nabla\cdot\Vec E=\frac{\rho}{\varepsilon_0}\tag{8}\]
\[\nabla\cdot\Vec D=\rho \tag{9}\]
と書かれる。\(~Maxwell~\)方程式であるが, (9)式の方がスマートである。
(5)式で
たぶん比例するだろうと書いたが, たぶんではなく正確に(5)式が成り立つのならば, (8)式は不要である。
残念ながら(5)式は正確ではない。以下はファインマン物理III電磁気学10章による。
\(\Vec D=\varepsilon\Vec E~\)のような式は物性を記述しようとする試みである。しかし物質は極めて複雑であって, このような式は実際正しくない。例えば\(~\Vec E~\)が大きくなると, \(\Vec D~\)は\(~\Vec E~\)に比例しなくなる。物質によっては\(~\Vec E~\)が割合に弱くても, 比例関係が破れている。また比例定数が\(~\Vec E~\)の時間的変化の速さに関係することもある。従ってこういう方程式は, フックの法則と同様,近似的である。
深い, 基礎方程式ではあり得ない。これに反して,\(\Vec E~\) についての基礎方程式
\[\nabla\cdot\Vec E=\frac{\rho}{\varepsilon_0}\]
\[\nabla\x \Vec E=0\]
は静電気についての
最も深く, 完全な理解を表明している。
ただし(以下筆者注), (9)式は物性研究には欠かせないもので, 複雑な現象を\(~\Vec D\), あるいは誘電率という数値で丸めて表現してくれる。限界を理解して使えば, これはこれで有用なものである。一つ例を挙げてみよう。
\(\bm{Lorentz - Lorenz}~\)(ローレンツ・ローレンス) の公式 光の屈折は電気双極子モーメントが引き起こす。
光が物質に入射すると, 入射電磁波の電場が物質を構成する原子(あるいは分子)に作用し, 原子には電気双極子が誘起される。その電気双極子は入射電磁波と同じ振動数で振動し, そこから新たな電磁波(2次波)が発振される。2次波には真空中を進む光速\(~c~\)をもつ電磁波と, 速度\(~c/n~\)を持つ電磁波の2つの成分が含まれる。
それらの光を重ね合わせると, 一部は入射した光と干渉して入射波を完全に打ち消し, 残った光は速度が\(~c/n~\)で伝播する光となる。これが屈折と呼ばれる現象である。
用語の整理
さてここで本題に入る前に, (1)電気感受率と(2)分極率について整理しておかなければならない。全く同じ意味で使っている教科書もあるが, 概ね次の様に使い分けているようである。\((Wikipedia)\)。
(1)電気感受率\(~\chi~\)(ファインマンの書では分極率と書かれている)
単位体積当たりの分極量,
マクロな量 \(\Vec P=Nq\bm{\delta}=N\chi\varepsilon_0 \Vec E \)
(2)分極率\(~\alpha~\)(ファインマンの書でも分極率)
原子1個の分極量,
ミクロな量 \(\bm{p}=\alpha\varepsilon_0 \Vec E \), 単位体積当たりでは\(\Vec P=N\bm{p}=N\alpha\varepsilon_0 \Vec E \)。
単位体積当たりでは同じ表現になって混乱するが, 例えば振動電場での電子の運動方程式
\[m\frac{d^2 x}{dt^2}+m\omega_0 ^2 x=q_e E\]
の解\(~\displaystyle x=\frac{q_e E}{m\omega_0 ^2}\)を使って,
\(~\displaystyle p=q_e x=\frac{q_e^2 E}{m\omega_0 ^2}\),
\(~\displaystyle \alpha=\frac{q_e^2}{\varepsilon_0 m\omega_0 ^2}\)
とすれば, \(\bm{p}=\alpha\varepsilon_0 \Vec E \)と表せる。こちらがミクロな量である。
その他, \(k=1+\chi, \varepsilon_r =1+\chi, \varepsilon=(1+\chi)\varepsilon_0, k-1=\alpha\ etc~\)等々, 初学者にとっては悩みの種となる様々な表現が使われるので注意されたい。
理論が発展する過程で, 分かりやすい表現を求めて, 試行錯誤してきた結果であろう。
ローレンツの局所場
今まで誘電体内の電場はいかにも一定のように述べてきたが, 原子が感じる電場は, 周囲の原子の影響を受け大きく変化している。極板間の電位差はこの全電場の線積分である。平均の電場が\(~E=V/d~\)ということである。
この局所的に原子が感じる電場を
ローレンツの局所場と呼び, 次の様に表される。
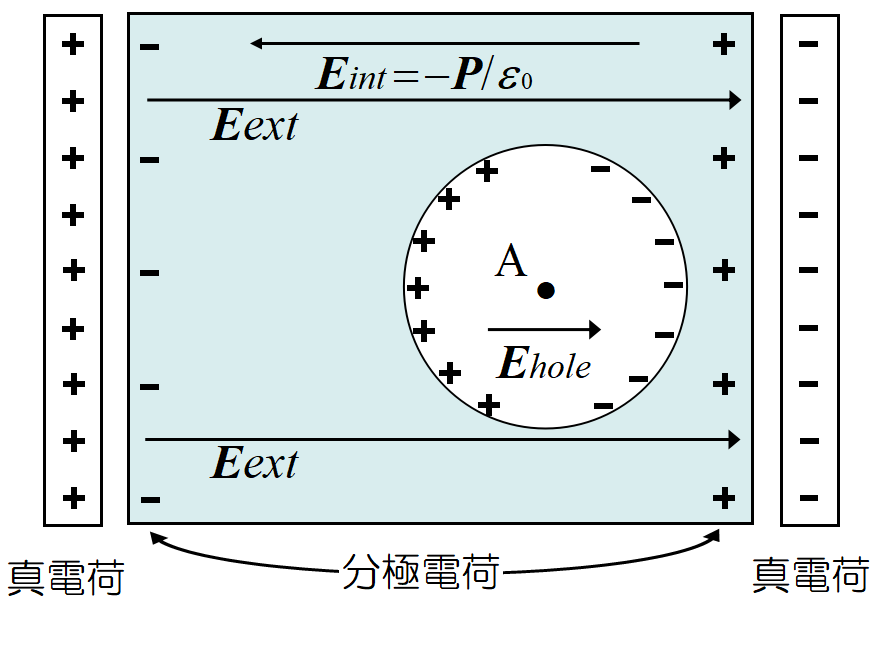
\[\Vec E_{loc}=\Vec E_{ext}+\Vec E_{int}+\Vec E_{hole} \]
\(\Vec E_{ext}\)はコンデンサーの極板にある電荷(真電荷)によって生じる電場\(~\displaystyle \frac{\Vec D}{\varepsilon_0}~\), \(\Vec E_{int}~\)は誘電体の表面に発生した分極電荷\(\pm P~\)による電場
\(\displaystyle -\frac{\Vec P}{\varepsilon_0}~\)である。
この和は既に述べたように, \(\displaystyle E=\frac{V}{d}\)として得られる電場
\[\Vec E=\Vec E_{ext}+\Vec E_{int}\]
である。そして\(\Vec E_{hole}\)は, 原子の大きさ程度にくり抜かれた球形の孔の中の電場である。
計算の結果によれば, A点の原子が感じる\(\Vec E_{hole}~\)は
\[\Vec E_{hole}=\frac{\Vec P}{3\varepsilon_0} \]
となる。球形の空洞表面に発生する分極電荷をクーロンの法則を用いて積分したものである。
空洞内の電場は平均の場より\(P/3\varepsilon_0~\)だけ大きい。つまり
\[\Vec E_{loc}= \Vec E+\frac{\Vec P}{3\varepsilon_0} \tag{10}\]
が原子を分極させる電場である。(10)式を用いると, 原子レベルの双極モーメント\(~\Vec P=N\bm{p}, \bm{p}=\alpha \varepsilon_0 \Vec E\) は
\[P=N\alpha\varepsilon_0\left(E+\frac{P}{3\varepsilon_0}\right) \]
である。\(P~\)について解いた
\[P=\frac{N\alpha}{1-(N\alpha/3)}\varepsilon_0 E \tag{11} \]
をクラウジウス・モソッティの式と呼ぶ。無極性分子のマクロな性質である誘電率と, ミクロな量である分極率を結び付ける。
\(E~\)は分極の効果を含んだ\(E=E_{ext}+E_{int}\)である。
\(\bm{Lorentz - Lorenz}~\)(ローレンツ・ローレンス) の公式
(11)式を, \(~\Vec P=\varepsilon_0(\varepsilon_r -1)\Vec E~\)を使ってまとめ直す*。
\[\frac{\varepsilon_r -1}{\varepsilon_r +2}=\frac{N\alpha}{3\varepsilon_0}\tag{12}\]
\(~n^2=\varepsilon/ \varepsilon_0~\)の関係があるから
\[\frac{n^2-1}{n^2+2}=\frac{N\alpha}{3\varepsilon_0}\tag{13}\]
となる。物質を構成する原子あるいは分子の分極と屈折率の関係を表すこの(12)式若しくは(13)式を, 独立に導いた2人の名をとって, \(\bm{Lorentz - Lorenz}~\)の公式という。
\[\alpha=\frac{q_e^2}{\varepsilon_0 m\omega_0 ^2}\]
であったから, 屈折率が光の波長によって異なる, 屈折率の分散が原子の分極率に結びついていることも分かる。
* \(\Vec D=\varepsilon_0\Vec E+ \Vec P=\varepsilon \Vec E~\)と決めたのだから, 何も新しい関係ではない。見た目をスッキリさせただけである。
ローレンツ・ローレンスの式は, 1869年にデンマークの物理学者・数学者ルードヴィヒ・ローレンスが弾性論から導いた。また1878年にはオランダの物理学者ヘンドリック・ローレンツが真空中と物質中の電磁気学の立場から導いた。後者がローレンツ力, ローレンツ変換で有名なローレンツである。因みにモソッティは1850年, クラウジウスは1879年である。\(Maxwell~\)方程式は1864年である。
電気双極子モーメント ここで解説しないと出番がなくなる。
電磁気学の解説では, 必ずと言ってよい程電気双極子の話が出てくる。この記事では屈折率との関係に触れたが, ぽつんと書かれている場合が多く, コンデンサーを除いて, 他の現象との関連性が分からない。
分子間力のファンデルワールス力は電気双極子同士の相互作用である。物理というより化学分野の現象で日常生活との係り合いが深い。量子力学では同じ数学的構造を持つ磁気双極子モーメントが重要な役割を果たす。また核物理学ではテンソル力成分となり, 素粒子物理学ではCP対称性の破れにも関係する。このように重要な量であるので, 解説をしておく。高校数学でO.Kである。
電気双極子モーメントのポテンシャル
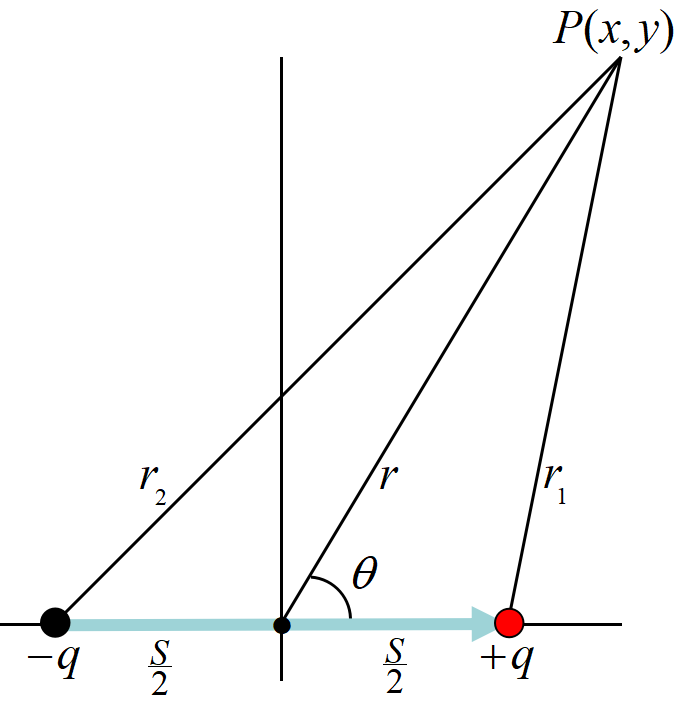
\(P~\)の位置ベクトルを\(~\bm{r}~\)とする。\(P~\)のポテンシャルは
\[\begin{align}
U(\bm{r})&=\frac{1}{4\pi\varepsilon_0}\frac{q}{r_1}
-\frac{1}{4\pi\varepsilon_0}\frac{q}{r_2} \\
&=\frac{q}{4\pi\varepsilon_0}\left(\frac{1}{\sqrt{r^2+\left(\frac{s}{2}\right)^2
-rs\cos\theta}}-\frac{1}{\sqrt{r^2+\left(\frac{s}{2}\right)^2+rs\cos\theta}}\right) \\
&=\frac{q}{4\pi\varepsilon_0 r}\left[\left(1+\frac{s^2}{4r^2}-\frac{s}{r}cos \theta\right)^{-\frac{1}{2}}-\left(1+\frac{s^2}{4r^2}+\frac{s}{r}cos \theta\right)^{-\frac{1}{2}}\right] \\
&\simeq \frac{q}{4\pi\varepsilon_0 r}\left[1-\frac{1}{2}\left(\frac{s^2}{4r^2}-\frac{s}{r}cos \theta\right)-1+\frac{1}{2}\left(\frac{s^2}{4r^2}+\frac{s}{r}cos \theta\right)\right] \\
&=\frac{qscos\theta}{4\pi\varepsilon_0 r^2} \\
&=\frac{\bm{p}\cdot\bm{r}}{4\pi\varepsilon_0 r^3}
\end{align}\]
最後にベクトルの形にしたが, ベクトル方程式は座標系に無関係になるので, この方が都合が良い場合が多い。
1行目から2行目は余弦定理を, 3行目から4行目は\(~x \ll 1~\)の時, \(~(1+x)^n \simeq 1+nx~\)を, 4行目から5行目は, \(~|\bm{p}|=qs~\)より, \(\bm{p}\cdot \bm{r}= qsr cos\theta~\)を用いた。
電気双極子モーメントの作る電場 ポテンシャルが逆2乗だから, 電場は逆3乗法則だろう。
電場はポテンシャルを座標で微分すれば良い。\(x~\)成分は
\[\begin{align}
E_x&= -\dd{U}{x} \\
&= -\dd{}{x}\left(\frac{1}{4\pi\varepsilon_0}\cdot\frac{p_x x+P_y y+p_z z}
{(x^2+y^2+z^2)^{\frac{3}{2}}}\right) \\
&= -\frac{1}{4\pi\varepsilon_0}\left( \frac{p_x}{(x^2+y^2+z^2)^{\frac{3}{2}}}
+(p_x x+p_y y+p_z z)\x \left(-\frac{3}{2}\right)\x 2x \x
\frac{1}{(x^2+y^2+z^2)^{\frac{5}{2}}} \right) \\
&= -\frac{1}{4\pi\varepsilon_0}\left(\frac{p_x}{r^3}
-\frac{3x(\bm{p}\cdot\bm{r})}{r^5}\right) \\
\end{align}\]
\(y~\)成分と\(z~\)成分も同様にして,
\[\Vec E(\bm{r})=-\frac{1}{4\pi\varepsilon_0}\left(\frac{\bm{p}}{r^3}
-\frac{3\bm{r}(\bm{p}\cdot\bm{r})}{r^5}\right) \]
予想通り距離の3乗で電場は弱くなる。