ローレンツは2人いる。オランダの\(~H.A.Lorentz~\)と, デンマークの\(~L.V.Lorenz~\)である。\(~H.A.Lorentz~\)が, ローレンツ変換, ローレンツ収縮の語源である。\(L.V.Lorenz~\)はローレンスとも言われ, マクスウェルとほとんど同等の電磁場の理論に到達していたが, 論文が分かりにくく評価は必ずしも高くはなかった。「遅延ポテンシャル」,「電磁ポテンシャルの一体化(4元化)」はローレンスの業績である。光の屈折に関する
ゲージ変換・ローレンツ共変・4元ベクトル
ベクトルポテンシャル・ゲージ変換(1)でベクトルポテンシャル\(~\Vec A~\)の実在性と, \(\Vec A~\)を用いた静磁場の解法を見てきた。この記事では電磁ポテンシャルを導入し, マックスウェル方程式が「ローレンツ共変」であることを導く。
電磁ポテンシャル
電場\(~\Vec E~\)を導くスカラーポテンシャル\(~\phi~\)と, 磁場\(~\Vec B~\)を導くベクトルポテンシャル\(~\Vec A~\)を総称して「電磁ポテンシャル」と呼ぶ。スカラー・・, ベクトル・・と呼ぶのが面倒だからという訳ではない。
それなりの理由があるのだが, 話が長くなるので今は形式的に覚えれば良い。名前は難しそうだが, 式変形は至って簡単である。
ファラデーの誘導法則\(~\nabla\x \Vec E+\partial \Vec B/\partial t=0~\)に\(~\Vec B=\nabla\x \Vec A~\)を代入すると
\[\nabla\x \Vec E+\dd{}{t}(\nabla\x \Vec A)=\nabla\x \left(\Vec E+\dd{\Vec A}{t}\right)=0 \]
を得る。\(~\nabla\x \Vec X=0 ~\)を満たす\(~\Vec X~\)は, 任意のスカラー関数の\(~grad~\)で表せるので,
\[\Vec E+\dd{\Vec A}{t}=-\nabla\phi\]
と置く。\(\nabla\phi~\)に-(マイナス)が付いているのは, \(\Vec E=-\nabla \phi~\)と対応させるためで, 数学的には不要である。
この関数\(~\phi~\), \(\Vec A~\)の組と, \(\Vec B=\nabla\x \Vec A~\)を合わせて電磁ポテンシャルと呼ぶ。
\[\Vec B=\nabla\x \Vec A \tag{1}\]
\[\Vec E=-\nabla\phi-\dd{}{t}\Vec A \tag{2}\]
とするのが普通である。電磁ポテンシャルは\(~-\partial\Vec A/\partial t~\)の項があるように, 時間変化する場の場合に有用である。
ローレンスゲージ
先ずガウスの法則を電磁ポテンシャルで表す。
\[\nabla\cdot\Vec E=\nabla\cdot\left(-\nabla\phi-\dd{\Vec A}{t}\right)
=-\triangle\phi-\nabla\cdot\dd{\Vec A}{t}=\frac{\rho}{\varepsilon_0}\]
\[\triangle\phi+\nabla\cdot\dd{\Vec A}{t}=-\frac{\rho}{\varepsilon_0} \tag{3} \]
次にマックスウェル・アンペールの法則は, 公式\(~\nabla\x (\nabla\x \Vec A)=\nabla(\nabla\cdot \Vec A)-\triangle \Vec A~\)を用いて,
\[\begin{align}
\nabla\x \Vec B-\varepsilon_0\mu_0 \dd{\Vec E}{t}
&=\nabla\x (\nabla\x \Vec A)-\varepsilon_0\mu_0\dd{}{t}\left(-\nabla\phi-\dd{\Vec A}{t}
\right) \\
&=-\left(\triangle\Vec A-\varepsilon_0\mu_0\dd{^2}{t^2}\Vec A \right)
+\nabla\left(\nabla\cdot \Vec A+\varepsilon_0\mu_0\dd{\phi}{t}\right)=\mu_0\bm{j}
\end{align}\]
より
\[\left(\triangle-\varepsilon_0\mu_0\dd{^2}{t^2} \right)\Vec A
-\nabla\left(\nabla\cdot \Vec A+\varepsilon_0\mu_0\dd{\phi}{t}\right)=-\mu_0\bm{j}\tag{4}\]
ここでいきなりだが(4)式, 左辺第2項のカッコ内を
\[\nabla\cdot \Vec A+\varepsilon_0\mu_0\dd{\phi}{t}=0\tag{5}\]
と置く。これをローレンスゲージと呼ぶ。こうやって良い理由は後で述べる。
(5)式を用いると(3)式は
\[\begin{align}
\triangle\phi+\nabla\cdot\dd{\Vec A}{t}&=\triangle\phi+\dd{}{t}(\nabla\cdot\Vec A) \\
&=\triangle\phi- \dd{}{t}\varepsilon_0\mu_0\dd{\phi}{t} \\
&=\triangle\phi- \varepsilon_0\mu_0\dd{^2\phi}{t^2}=-\frac{\rho}{\varepsilon_0}
\end{align} \]
となるから, (3), (4)式はそれぞれ,
\[\left(\triangle-\varepsilon_0\mu_0\dd{^2}{t^2}\right)\phi=-\frac{\rho}
{\varepsilon_0}\tag{6}\]
\[\left(\triangle -\varepsilon_0\mu_0\dd{^2}{t^2}\right)\Vec A =-\mu_0\bm{j}\tag{7}\]
と表せる。
ゲージ変換 解の任意性
ところでいきなり導入した(5)式は妥当性があるのだろうか?
任意のスカラー関数を\(~\chi~\)とする。
\[\Vec A_L=\Vec A+\nabla\chi \tag{8}\]
\[\phi_L=\phi-\dd{}{t}\chi \tag{9}\]
としたとき, \(\Vec A_L,\,\phi_L~\)が電磁ポテンシャルを満たすことを確かめよう。
\[\nabla\x \Vec A_L=\nabla\x \Vec A+\nabla\x \nabla\chi=\nabla\x \Vec A=\Vec B \]
\[\begin{align}
-\nabla\phi_L-\dd{\Vec A_L}{t}
&=-\nabla\left(\phi-\dd{}{t}\chi\right)-\dd{}{t}(\Vec A+\nabla\chi) \\
&=-\nabla\phi+\cancel{\nabla\dd{}{t}\chi}-\dd{\Vec A}{t}-\cancel{\dd{}
{t}\nabla\chi} \\
&=-\nabla\phi-\dd{\Vec A}{t}=\Vec E \\
\end{align}\]
となり確かに電磁ポテンシャルとなっている。\(\chi~\)は任意に選べるので, (8)式および(9)式を満たす\(~(\phi, \Vec A)~\)は無数にある。
この\(~(\phi,\Vec A)~\)から\(~(\phi_L,\Vec A_L)~\)への変換を
ゲージ変換と呼ぶ。あとはこの無数の組み合わせの中から(5)式を満たす\(~(\phi_L,\Vec A_L)~\)を選べば良い。
物理学の世界では, このように見方を変えることをゲージ変換, 見方を変えても値の変わらないことを
ゲージ不変性, または,
ゲージ対称性と呼ぶ。
\(\chi~\)を選んでみよう。ローレンスゲージ(5)式を
\[\begin{align}
\nabla\cdot\Vec A_L+\varepsilon_0\mu_0\dd{\phi_L}{t}
&=\nabla\cdot(\Vec A+\nabla\chi)+\varepsilon_0\mu_0\dd{}{t}\left(\phi-\dd{}{t}\chi\right)\\
&=\nabla\cdot\Vec A+\varepsilon_0\mu_0\dd{\phi}{t}
+\left(\triangle-\varepsilon_0\mu_0\dd{^2}{t^2}\right)\chi \\
\end{align}\]
と変形する。この式が 0, すなわち
\[\left(\triangle-\varepsilon_0\mu_0\dd{^2}{t^2}\right)\chi=-\left(\nabla\cdot\Vec A+\varepsilon_0\mu_0\dd{\phi}{t}\right) \]
となるように\(~\chi~\)を選べばローレンスゲージ(5)式が成り立つという訳である。
まあ, 実際にこれから\(~\chi~\)を決めるのは至難ではあるが!
唐突な式変形が目立つが, 先人たちの労苦をそのまま写した為である。我ら凡才が少々考えたところで, 得られるものではない。
ダランベルシアン 4元ベクトルはもう少し後。
(再掲)マックスウェル方程式は, 電磁ポテンシャルを用いると, ローレンスゲージ(5)の下で
\[\nabla\cdot \Vec A+\varepsilon_0\mu_0\dd{\phi}{t}=0\tag{5}\]
\[\left(\triangle-\varepsilon_0\mu_0\dd{^2}{t^2}\right)\phi=-\frac{\rho}
{\varepsilon_0}\tag{6}\]
\[\left(\triangle -\varepsilon_0\mu_0\dd{^2}{t^2}\right)\Vec A =-\mu_0\bm{j}\tag{7}\]
と書ける。(6), (7)式の左辺の演算子は全く同じ形をしているので, これを
\[\square\equiv\left(\triangle -\varepsilon_0\mu_0\dd{^2}{t^2}\right)\tag{10} \]
とおいて, これをダランベール演算子, ダランベルシアンと呼ぶ。これを用いるとマックスウェル方程式は,
\[\square\phi=-\frac{\rho}{\varepsilon_0}\quad \square\Vec A=-\mu_0\bm{j}\tag{11} \]
の2つの式で表せる。\(\square~\)は別名4次元ラプラシアンとも呼ばれる。その意味では後述する
4元ベクトルに作用する演算子が正しいが。
ダランベルシアンのローレンツ共変性
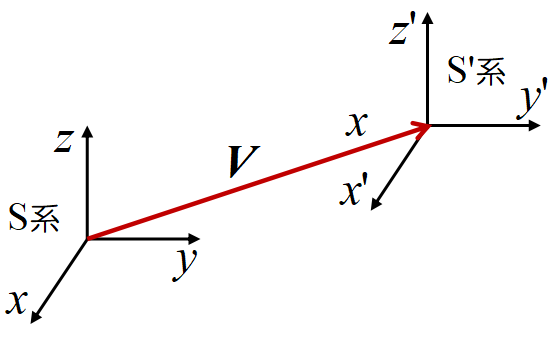
慣性系\(~S~\)に対して\(~x~\)軸方向に\(~V~\)で進む慣性系\(~S'~\)を考え, \(~S,\,S'~\)でのダランベール演算子が等しくなることを示そう。
\[\gamma=\frac{1}{\sqrt{1-(V^2/c^2)}},\;\beta=\frac{V}{c}\]
として, ローレンツ変換,
\[ct'=\gamma(ct-\beta x),\quad x'=\gamma(-\beta ct+x),\quad y'=y,\quad z'=z \tag{12}\]
より,
\[\begin{align}
\dd{}{t}&=\dd{t'}{t}\dd{}{t'}+\dd{x'}{t}\dd{}{x'}=\gamma\dd{}{t'}-\gamma c \beta\dd{}{x'}\\
\dd{}{x}&=\dd{t'}{x}\dd{}{t'}+\dd{x'}{x}\dd{}{x'}=-\gamma\frac{\beta}{c}\dd{}
{t'}+\gamma\dd{}{x'}
\end{align}\]
を用いて,
\[\begin{align}
\dd{^2}{x^2}-\frac{1}{c^2}\dd{^2}{t^2}
&=\left(-\gamma\frac{\beta}{c}\dd{}{t'}+\gamma\dd{}{x'}\right)^2
-\frac{1}{c^2}\left(\gamma\dd{}{t'}-\gamma c\beta \dd{}{x'}\right)^2 \\
&=\gamma^2(1-\beta ^2)\left(\dd{}{x'}\right)^2-2\left(\gamma^2\frac{\beta}{c}
-\gamma ^2\frac{\beta}{c}\right)\left(\dd{}{x'}\right)\left(\dd{}{t'}\right)
-\frac{1}{c^2}\gamma^2(1-\beta^2)\left(\dd{}{t'}\right)^2 \\
&=\dd{^2}{x'^2}-\frac{1}{c^2}\dd{^2}{t'^2}
\end{align}\]
を得る。2行目~3行目で
\[\gamma^2(1-\beta^2)=\left(\frac{1}{\sqrt{1-(V^2/c^2)}}\right)^2(1-(V^2/c^2))=1\]
を用いた。よって,
\[\begin{align}
\square&=\dd{^2}{x^2}+\dd{^2}{y^2}+\dd{^2}{z^2}-\frac{1}{c^2}\dd{^2}{t^2} \\
&=\dd{^2}{x'^2}+\dd{^2}{y'^2}+\dd{^2}{z'^2}-\frac{1}{c^2}\dd{^2}{t'^2}=\square'
\end{align}\]
と, 慣性系\(~S~\)でのダランベルシアンと慣性系\(~S'~\)でのダランベルシアンが等しくなる。
ダランベルシアンは\(~x~\)軸方向の変換で
ローレンツ共変である。
ここで, 電流密度, あるいは一見するとスカラーの電荷密度がなぜ座標と同じくローレンツ変換を受けるのか不思議に思う読者がいるかもしれない。それは密度, つまり体積が関係するからである。一辺の長さが\(~l_0~\)の立方体の中に電子が\(~N~\)個あるとする。電気量は\(~Ne~\)であり, この立方体の電荷密度は
\[\rho_0=\frac{Ne}{l_0^3}\]
である。観測者に対して速度\(~V~\)で\(~x~\)軸方向に運動している電荷を観測すると, \(x~\)方向のみ辺の長さが短縮するから, 電荷密度は
\[\rho=\frac{Ne}{l_0\sqrt{1-(V/c)^2}}\]
と観測される。電荷密度に速度を掛けると電流密度となるから
\[\bm{j}=\rho\Vec V=\frac{Ne}{l_0^3\sqrt{1-(V/c)^2}}\cdot\Vec V \]
となる。以上によって, 電荷密度\(~\rho\), 電流密度\(~\bm{j}~\)がローレンツ変換を受ける。
共変でない変換とは ガリレイ変換
共変形式のテキスト, ウェブサイトを見ると, 綺麗な共変変換ばかりである。そうでない変換の例を見てみよう。
ガリレイ変換, \(t'=t,\,x'=x-Vt,\,y'=y,\,z'=z~\)より,
\[\begin{align}
\dd{}{t}&=\dd{t'}{t}\dd{}{t'}+\dd{x'}{t}\dd{}{x'}=1\cdot\dd{}{t'}-V\dd{}{x'} \\
\dd{}{x}&=\dd{t'}{x}\dd{}{t'}+\dd{x'}{x}\dd{}{x'}=0+1\cdot\dd{}{x'}
\end{align}\]
である。これを用いてダランベルシアンを求めると,
\[\begin{align}
\dd{^2}{x^2}-\frac{1}{c^2}\dd{^2}{t^2}
&=\left(\dd{}{x}\right)^2-\frac{1}{c^2}\left(\dd{}{x}\right)^2 \\
&=\left(\dd{}{x'}\right)^2-\frac{1}{c^2}\left(\dd{}{t'}-V\dd{}{x'}\right)^2 \\
&=\left(1-\frac{V^2}{c^2}\right)\dd{^2}{x'^2}+\frac{2V}{c^2}\dd{^2}{t'\partial x}
\end{align}\]
と無残な形となる。これは期待されるダランベルシアン,
\[\square'=\dd{2}{x'^2}-\frac{1}{c^2}\dd{^2}{t'2}\]
とは異なり, マックスウェルの波動方程式はガリレイ変換では同じ形にならない(共変ではない)。
電気力線, 磁力線として時には目で見える(磁石の上の鉄粉), 電場\(~\Vec E~\), 磁場\(~\Vec B~\)は, そのままでは観測する座標系によって, 方程式の形が変わってしまう。
一方, より抽象的な電磁ポテンシャルは観測する立場が変わっても同じ物理法則は, 同じ形で表される。正確には同じ形で表せる変換, ローレンツ変換が存在する。
そうするとローレンツ変換の方がガリレイ変換よりも, あるいは電磁ポテンシャルの方が,電場,磁場より本質的な物理量であると考えても良さそうである。
量子力学, 相対論もそうであるが, 実存の世界は, 我々の日常生活の感覚とは異なっているのかもしれない.
ところで, ローレンツ変換もガリレイ変換も, 等速運動は\(~x~\)方向のみであるが, これで一般性を失わないのだろうか?
\(~x~\)方向のみで良いのである。図を見れば明らかなように, \(y,z~\)方向に速度を持つ場合, 速度\(~\Vec V~\)の方向に座標を取り直せば良い。
言い換えれば, \(y,z~\)の2方向を加えて一般化しても, 新しい情報は得られないということである。
それでも一般化するのは, 一般相対論で重要な役目を果たす
エネルギー・運動量テンソル, 電磁場テンソルを用いるとき必要になるからである。
4元ポテンシャル・4元電流密度 カッコイイだけか?
(6), (7)式を見れば誰だって一つにまとめたくなる。まとめる為に単位を合わせよう。
(6)式の両辺を\(~c~\)で割り, \(c^2=1/\varepsilon_0\mu_0~\)を用いると
\[\left(\triangle-\varepsilon_0\mu_0\dd{^2}{t^2}\right)\frac{\phi}{c}
=-\frac{\rho}{\varepsilon_0 c}=-\mu_0\rho c\]
となる。\(\rho c~\)は電荷密度×速度なので電流密度を表す。\(V~\)ではなく, \(c~\)で割るのは, 右辺を\(~-\mu_0 j ~\)の形にするためである。
改めて
\[\Vec A=\left(\frac{\phi}{c},A_x,A_y,A_z\right) \]
\[\bm{j}=(\rho c,\,j_x,\,j_y,\,j_z) \]
と書くと, (11)式は一つにまとめて
\[\square\Vec A=-\mu_0\bm{j} \tag{13}\]
と表せる。\(\bm{j}~\)を
4元電流密度, \(\Vec A~\)を
4元ポテンシャルと呼ぶ。
さてこの4元電流密度であるが, ただ単にカッコイイだけなのか, それとも4元化する理由があるのか?
正解は後者である。次の「相対論との関わり」で説明する。その前に,
変化する電磁場
今までは電荷は位置的にも, 時間的にも固定されていた静電場での話であった。
(1)位置は変わらず, 電荷密度が時間と共に変わる
(2)位置が変化する, すなわち電荷が運動する
場合, 電磁ポテンシャルはどのように表現されるのだろうか?
(2)はリエナール・ウィーヘルト・ポテンシャルであるが, 多くの予備知識が必要なので, 相対論で改めて取り上げる。
遅延ポテンシャル 電荷の位置は固定。電荷密度が変化。
原点に\(~q(t)~\)で変化する点電荷があるとする。この電荷が作り出すポテンシャルは球対称であろうから\(~\phi(r,t)~\)と表される。
演算子も球面極座標で表すと見通しが良くなる。球面極座標のラプラシアンは(公式集を見て下さい)
\[
\triangle=\frac{1}{r^2}\dd{}{r}\left(r^2\dd{}{r}\right)+\frac{1}{r^2\sin\theta} \dd{}{\theta}\left(\sin\theta\dd{}{\theta}\right)+\frac{1}{r^2\sin\theta}\dd{^2}{\phi^2}
\]
であるが, 球対称な空間では\(~r~\)以外の微分は落として良いので
\[\begin{align}
\triangle\phi&=\frac{1}{r^2}\dd{}{r}\left(r^2\dd{}{r}\right)\phi \\
&=\frac{1}{r^2}\left(2r\dd{}{r}+r^2\dd{^2}{r^2} \right)\phi \\
&=\frac{2}{r}\dd{\phi}{r}+\dd{^2\phi}{r^2} \\
&=\frac{1}{r}\dd{^2}{r^2}(r\phi)
\end{align}\]
従ってスカラーポテンシャルの波動方程式は,
\[\frac{1}{r}\dd{^2}{r2}(r\phi)-\frac{1}{c^2}\dd{^2}{t^2}\phi=0 \]
両辺に\(~r~\)をかけて
\[\left(\dd{^2}{r^2}-\frac{1}{c^2}\dd{^2}{t^2}\right)(r\phi)=0 \tag{14} \]
ここで, \(r=0~\)以外の部分では\(~\rho=0~\)だから, 右辺は 0 とした。厳密には\(~r=0~\)ではデルタ関数を使って処理しなければならないが, 省略した。
(14)式は\(~r\phi~\)に対する一次元の波動方程式となっており, この解は波動方程式の一般解より
\[r\phi=f(r-ct)+g(r+ct) \]
である。電磁ポテンシャルの場合は
\[r\phi=f(t-r/c)+g(t+r/c)\tag{15} \]
と書くのが一般的である。(15)式より
\[\phi=\frac{f(t-r/c)}{r}+\frac{g(t+r/c)}{r}\tag{16} \]
が, 原点に電荷密度\(~\rho(t)~\)があるときのスカラーポテンシャルである。
\(f~\)は原点から外向きに出てゆく進行波, \(g~\)は逆に原点に向かって入ってくる後退波である。
\(g~\)は数学的には何の問題もないが, 物理的には不自然なので, 通常は\(~f~\)のみを使う。
\(~f~\)は原点の波動が時間\(~t=r/c~\)だけ遅れてやってくるので, 原点の電荷を\(~Q(t)~\)とすれば,
\[\phi=\frac{1}{4\pi\varepsilon_0}\frac{Q(t-r/c)}{r} \tag{17}\]
これが電荷密度が変化する点電荷の作るスカラーポテンシャルである。クーロンポテンシャルと同じ形であるが, 光速の伝搬時間だけ遅れたポテンシャルを感じるのである。
電荷が連続的に分布する場合は, (17)の解を重ね合わせ
\[\phi(\bm{r},t)=\frac{1}{4\pi\varepsilon_0}\int\frac{\rho(\bm{r'},t-|\bm{r}-\bm{r'}|/c)}{|\bm{r}-\bm{r'}|} d\bm{r'}\tag{18} \]
とすればよい。\(d\bm{r'}~\)は正しくは\(~d\bm{r'}^3~\)で体積積分である。
ベクトルポテンシャルも同様の方法によって
\[\Vec A(\bm{r},t)=\frac{\mu_0}{4\pi}\int\frac{\bm{j}(\bm{r'},t-|\bm{r}-\bm{r'}|/c)}{|\bm{r}-\bm{r'}|}d\bm{r'} \tag{19} \]
(18), (19)式を遅延ポテンシャルと呼ぶ。原点の電荷密度, あるいは電流密度の変化の影響が, 時間\(~r/c~\)だけ遅れて現れるのでこう呼ぶ。
数学的には問題ないが, 不自然な\(~t+r/c~\)の方は, 時間\(~r/c~\)だけ, 先に現れるので先進ポテンシャルまたは先進波と呼ぶ。アニメやSFで, 過去との通信とか, ワープの理論として使われる。
相対性理論との関わり
相対論は4次元が基本。 詳しく知りたい読者は, 石井俊全 一歩一歩相対論を参照。とても丁寧に書かれています。
電磁気学では電流密度を4元化した。何か神秘的な4次元電流があるのだろうか?
そうではない。ローレンツ共変とするために4つのパラメーターが必要なのである。
ローレンツ変換は, \(ct'=\gamma(ct-\beta x),\;x'=\gamma(-\beta ct+x),\;y'=y,\;z'=z~\)の4つであるが, \(y,\,z~\)は何も変わらないので, 実質は\(ct'=\gamma(ct-\beta x),\;x'=\gamma(-\beta ct+x)~\)の2つである。
もしこの時, 物理量が\(~x~\)のみだったら, 変換されるのは\(~x'~\)だけで, ローレンツ共変とはならない。もう一つの次元, \(ct~\)が必要なのである。
3次元のままでは, 直交変換についてしか共変にならないので, 4元化するのである。
言い方を変えれば, ローレンツ変換で共変になるように物理法則を書き換えることを4元化と言う。(←石井俊全 一歩一歩相対論 p348)
「アインシュタインの強い等価原理」すなわち, 異なる慣性系でも物理法則は同じ形を実現するには4元ベクトルが必要である。
特殊相対論の位置ベクトルは, 4元座標で, \((ct,\,x,\,y,\,z)~\)となる。時間軸を\(~ct~\)としたのは, 次元を合わせるためである。
\[\bm{x}^{\mu}=(ct,x,y,z)=(x^0,x^1,x^2,x^3) \]
と書く。上付きの添え字はべき乗ではなく, \(x^{\mu}~\)が反変ベクトルであることを表している。
相対論では\(~x_{\nu}~\)を共変ベクトルとして使い分ける。
4元速度 それでも共通の時間が欲しい。
慣性系\(~S~\)に対して\(~x~\)軸方向に\(~V~\)で進む慣性系\(~S'~\)を考え, 夫々の系での3次元速度\(~\bm{\upsilon} ,\,\bm{\upsilon'}\)と\(~V~\)との関係を見よう。
ローレンツ変換\(~ct'=\gamma(ct-\beta x)~\)の両辺を\(~c~\)で割って\(~t~\)で微分すると
\[\begin{align}
\frac{dt'}{dt}
&=\gamma\left(1-\frac{\beta}{c}\frac{dx}{dx'}\right)=\gamma\left(1-
\frac{v_xV}{c^2}\right) \\
&=\frac{1-\upsilon_xV/c}{\sqrt{1-(V^2/c^2)}}=\frac{\sqrt{1-(|\bm{\upsilon}|^2/c^2)}}
{\sqrt{1-(|\bm{\upsilon'}|^2/c^2)}}\tag{20}
\end{align}\]
より
\[\sqrt{1-(|\bm{\upsilon}|^2/c^2)}\,dt=\sqrt{1-(|\bm{\upsilon'}|^2/c^2)}\,dt'\tag{21} \]
が得られる。(20)式の最後の変形は(石井俊全一歩一歩相対論p355参照)。
相対論では絶対時間は無いとされるが, (21)式の(微小)時間は慣性系によらない不変量である。そこで
\[d\tau=\sqrt{1-(|\bm{\upsilon}|^2/c^2)}\,dt=\sqrt{1-(|\bm{\upsilon'}|^2/c^2)}\,dt' \]
とし, 固有時と呼ぶ。慣性系によらないので, ガリレイ変換の絶対時に近いものとして使える。
4元位置座標\(~\bm{x}^{\mu}=(ct,x,y,z)~\)を固有時\(~d\tau~\)で割った(微分した)ものを速度として,
\[u^1=\frac{dx}{d\tau}=\frac{1}{\sqrt{1-(|\bm{\upsilon'}|^2/c^2)}}\frac{dx}{dt}
=\frac{\upsilon_x}{\sqrt{1-(|\bm{\upsilon'}|^2/c^2)}}\]
に倣って,
\[u^0=\frac{c}{\sqrt{1-(|\bm{\upsilon'}|^2/c^2)}},\,u^1=\frac{\upsilon_x}{\sqrt{1-(|\bm{\upsilon'}|^2/c^2)}},\,u^2=\frac{\upsilon_y}{\sqrt{1-(|\bm{\upsilon'}|^2/c^2)}},\,u^3=\frac{\upsilon_z}{\sqrt{1-(|\bm{\upsilon'}|^2/c^2)}},\,\tag{22} \]
を4元速度と呼ぶ。
4元運動量 あの有名な\(~E=mc^2~\)はこうやって得られる。
(22)式, 4元速度に質量\(~m~\)をかけた
\[P^0=mu^0,\;P^1=mu^1,\;P^2=mu^2,\;P^3=mu^3 \]
を4元運動量と呼ぶ。因みに\(~\bm{p}=(m\upsilon_x,\,m\upsilon_y,\,m\upsilon_z)~\)である。
ここで\(~\eta_{ij}u^iu^j~\)(ミンコフスキー計量)は
\[\begin{align}
\eta_{ij}u^iu^j&=-(u^0)^2+(u^1)^2+(u^2)^2+(u^3)^2 \\
&=-\left( \frac{c}{\sqrt{1-(|\bm{\upsilon}|^2/c^2)}}\right)^2
+\left( \frac{\upsilon_x}{\sqrt{1-(|\bm{\upsilon}|^2/c^2)}}\right)^2 +\left( \frac{\upsilon_y}{\sqrt{1-(|\bm{\upsilon}|^2/c^2)}}\right)^2
+\left( \frac{\upsilon_z}{\sqrt{1-(|\bm{\upsilon}|^2/c^2)}}\right)^2 \\
&=-\frac{1}{1-(|\bm{\upsilon}|^2/c^2)}(-c^2+|\bm{\upsilon}|^2)=-c^2
\end{align}\]
である。\(~\eta_{ij}u^iu^j~\)は, アインシュタインが数学に最大の貢献をした発明だと自慢した 「アインシュタインの縮約記法」で, 上下に同じ添え字が現れたときは, \(\sum~\)の記号を省略し, その添え字に関する合計をする。
この\(~\eta_{ij}u^iu^j=-(u^0)^2+(u^1)^2+(u^2)^2+(u^3)^2=c^2~\)を\(~t~\)で微分して\(~2~\)で割ると,
\[\begin{align}
&-u^0\frac{du^0}{dt}+u^1\frac{du^1}{dt}+u^2\frac{du^2}{dt}+u^3\frac{du^3}{dt}=0 \\
&-c\frac{dP^0}{dt}+\upsilon_x\frac{dP^1}{dt}+\upsilon_y\frac{dP^2}{dt}+\upsilon_z\frac{dP^3}{dt}=0 \\
&-c\frac{dP^0}{dt}+\upsilon_x f_x+\upsilon_y f_y+\upsilon_z f_z=0 \\
& \frac{d(cP^0)}{dt}=f_x\upsilon_x +f_y\upsilon_y +f_z\upsilon_z \tag{23}
\end{align} \]
が得られる。
(23)式の右辺は\(~\bm{f}\cdot\bm{\upsilon}~\), すなわち, 力×速度で仕事率である。すると左辺の\(~cP^0~\)は物体の持つ全エネルギー\(~E=cP^0~\)と考えて良い。
全エネルギー\(~E=cP^0~\)は,
\[\begin{align}
E&=c\left(\frac{mc}{1-\sqrt{1-(|\bm{\upsilon}^2/c^2)}}\right) \\
&=mc^2(1-(|\bm{\upsilon}|^2/c^2))^{-\frac{1}{2}} \\
&\approx mc^2+\frac{1}{2}m|\bm{\upsilon}|^2 \tag{24}
\end{align}\]
と表される。(24)式右辺第2項は, 質量\(~m~\), 速度\(~\bm{\upsilon}~\)を持つ物体の運動エネルギーを表している。\(\bm{\upsilon}=0~\)のときが有名な\(~E=mc^2~\)である。
ローレンツ変換(12)は, マックスウェルもローレンツも思い及ばなかった, 時空に対する新しい概念を内在していた。ローレンツ変換の正しい解釈はアインシュタインによってなされた。
エドワード M. パーセルは「アインシュタインの相対論的不変性は長い間認められなかった。しかし偶然だが, 物理学はずっと以前に相対論的に不変な理論 "マックスウェルの電磁気理論" を持っていた」と述べている。