極値の必要条件
関数\(f(x)\)が\(x=a\)で極値をとれば\(f'(a)=0\)が成り立つ。しかし、この逆の\(f'(a)=0\) といっても極値とは限らない。
このことをテイラー展開を使って証明します。
テイラー展開の式は1次項、2次項、…n次項からなり、高次の項は低次の項を補正している。
次数が増えるに従い補正量は減り、点\(a\)近傍の局所では、初めの低次の項により、高い近似を得る。
2次までの展開を書くと:
\(f(x)=f(a)+\frac{f'(a)}{1!}(x-a)\)\(+\frac{f''(a)}{2!}(x-a)^2+R_n\)
\(R_n\):剰余項(誤差項)と3次項以降は極大・極小の判定には影響がないものとする。
点\(a\)近傍の\(x=a\pm δ\) のテイラー展開を考える。
すなわち、\(a\)近傍の局所領域における \(f'(x)\) を調べる。
点\(a\) において極大のとき:
(極小のときも同様な考えです。)
\(x=a+δ\) と \(δ=x-a\) であることに留意して
\(f(a+δ)-f(a)=f'(a)(δ)\)\(+\frac{1}{2}f''(a)(δ)^2+R_n\)…ⓐ
\(f(x)=f(a+δ)\)\(=f(a)+f'(a)(x-a)\) \(+\frac{1}{2}f''(a)(x-a)^2+R_n\)
\(x=a-δ\) と \(-δ=x-a\) であることに留意して
\(f(a-δ)-f(a)=f'(a)\color{red}{(-δ)}\) \(+\frac{1}{2}f''(a)(-δ)^2+R_n\)…ⓑ
\(f(x)=f(a-δ)\)\(=f(a)+f'(a)(x-a)\) \(+\frac{1}{2}f''(a)(x-a)^2+R_n\)
2式の左辺は負であり、\(f''\) の項は非負(∵2乗項)であるから 式ⓐ では\(f'(a)\gt 0\)、 式ⓑでは \(f'(a)\lt 0\) である。
これを満たす 点a の1次項は \(f'(a)=0\)であり、これが極値をもつ必要条件である。
これは必要条件であるが十分条件ではない。 なぜなら、例として\(f(x)=x^3\)は\(f'(0)=0\)だが極小、極大でもない。
\(f(x)=x^3\) は\(x=0\) 近傍での\(f'(x-δ)\gt 0\)、\(f'(x+δ)\gt 0\)であり、極値にはならない。
(極値のとき、その前後で微分係数の符号が変化しなければならない。)
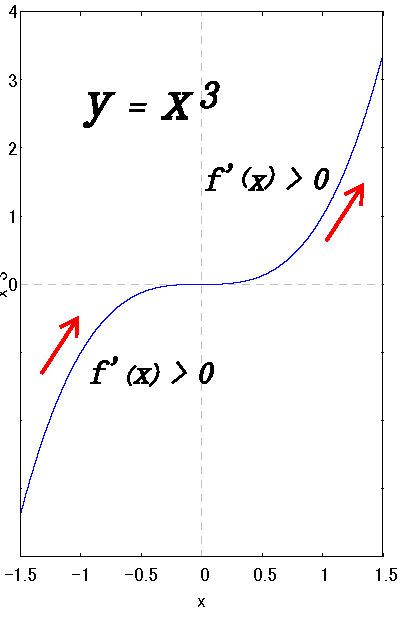
\(f=x^3\) 極値点はない
1変数関数の極値の定義
【参照先】
次に\(f'(a)=0 \) のとき、極値か否かの判定をテイラーの定理式を用いておこなう。
\(f'(a)=0\) だから次式が成り立つ。
\(f(x)=f(a)+\frac{1}{2}f''(a)(x-a)^2+R_n\)
\(R_n\)は微小として無視、また\((x-a)^2 \gt 0\) である。
\(f(x)-f(a)=+\frac{1}{2}f''(a)(x-a)^2\)
上式より、\(f"(a)\) の正負により次のように 極大、極小の判定が行える。
\(\color{red}{f''(a)\gt 0}\) なら \(f(x)\gt f(a)\) だから \(f(a)\) は極小
\(\color{red}{f''(a)\lt 0}\) なら \(f(x)\lt f(a)\) だから \(f(a)\) は極大
また \(f''(a)=0\) のときどうなるか、さらに高次のテイラー展開を調べることになる。
3次(奇数次)のときは\(f^{(3)}(a)\ne 0\) でも極大・極小の判定はできない:
\(f(x)-f(a)=+\frac{1}{6}f^{(3)}(a)(x-a)^3+R_n\)
\(f^{(3)}(a)\ne 0\)のとき、\(f(x)-f(a)\)は右辺の\((x-a)^3\) の符号が変動(3乗だから)するので\(f(a)\) は極値でない。
これより極値の判定には2回以上の微分回数\(n\)が偶数の\(f^{(n)}(a)\ne 0\) のときである。
まとめると、f'(a)=0 により停留点が得られたあと、f のn 回微分 の \(f^{(n)}(a)\ne 0\) となる n が最初の偶数のとき:
\(f^{(n)}(a)\)が「正なら\(f(a)\) は極小」 「負なら\(f(a)\) は極大」と判定できる。
2変数関数の極値
2変数関数の極値の定義
2変数関数\(z=f(x,y)\) が点\((a,b)\)の近傍において(局所的な概念から)
\(f(a,b)\gt f(x,y)\)\(\quad\) \((x,y)\ne (a,b)\)のとき
\(f(a,b)\)を
極大値、\((a,b)\)を
極大点という。
\(f(a,b)\lt f(x,y)\)\(\quad\) \((x,y)\ne (a,b)\)のとき
\(f(a,b)\)を
極小値、\((a,b)\)を
極小点という。
さて、下図は
鞍点(saddle point)を示している。(馬の鞍に似ている)
ある方向から見ると極大(x=0でのx-z平面)、別の方向から見ると極小(y=0でのy-z平面)である停留点である。
言い方を換えると極大でも、極小でもない停留点である。
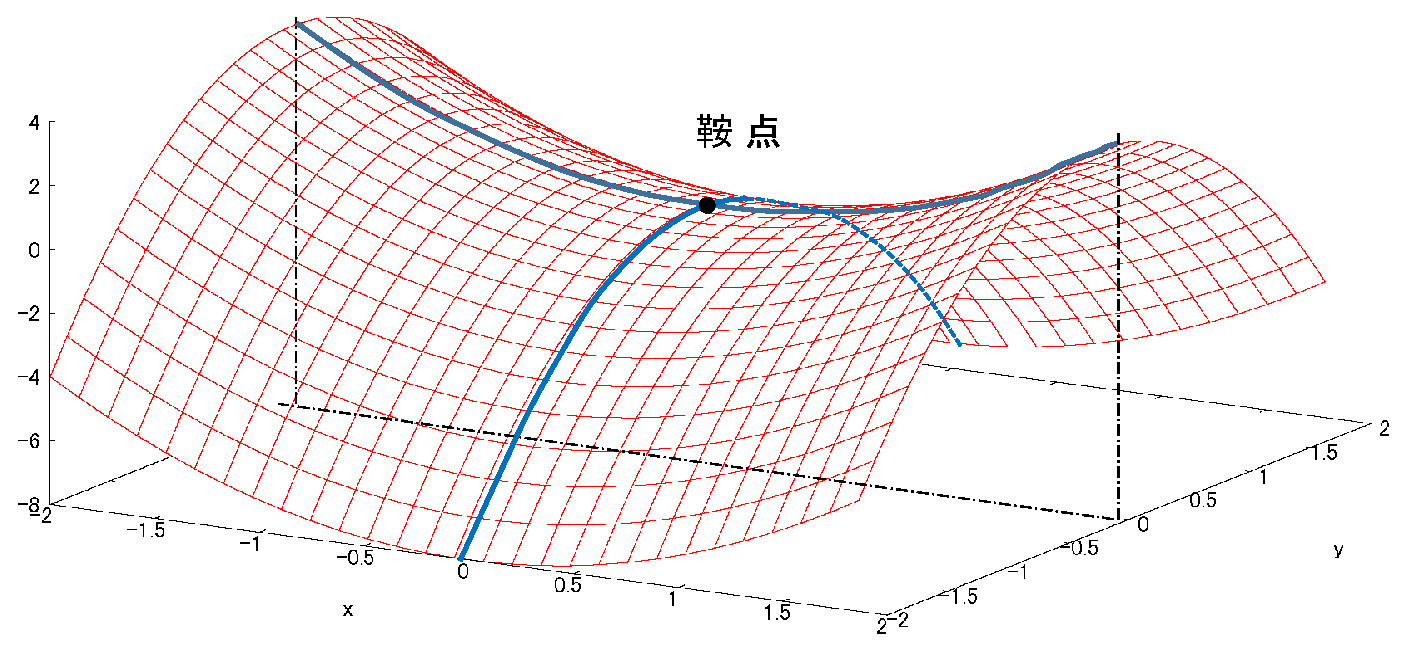
fig1: \(f=x^2-2y^2\)
2変数関数の極値
2変数関数の極値を求めるには1変数関数のときと同様にその関数の
・1階の偏微分により停留点を求め。
・2階の偏微分と判別式(後述)により極値の判定をする。
(1)停留点
(極値となる必要条件)
2変数関数 \(z=f(x,y)\)のグラフは曲面、曲面の極値は「極大は山の頂点」、「極小は谷底」である。
極大・極小の共通点は極値点(a,b)での接平面が x-y平面に平行(水平面)である。
従って極大・極小の停留点となる条件は接平面の傾きが 0 のときである。
これは接平面の方程式はテイラー展開の1次近似式であり、この1次項が 0 となることである。
すなわち極値となる条件は
\(\underline{f_x(a,b)}=0\)\(\ \ ,\ \)\(\underline{f_y(a,b)}=0\)
である。…この(a,b)が停留点です。
テイラー展開の公式は
\(f(a+h,y+k)=\displaystyle \sum_{m=0}^{n-1} \frac{1}{m!}
(\ h\pder{}{x}+ k \pder{}{y}\ )^{\ m} \ f\ (a,b)\) \(+R_n \)
\(h=x-a,\ k=y-b\) 、3次項以上と\(R_n\)項を 0 として
上の∑の式を展開した1次近似式は:
\(f(x,y)=f(a,b)+f_x(a,b)(x-a)\)\(+f_y(a,b)(y-b)\)
これより接線の方程式は
\(f(x,y)-f(a,b)=\underline{f_x(a,b)}(x-a)\)\(+\underline{f_y(a,b)}(y-b)\)
1変数関数と同様に左辺が0 となるのは\(f_x,f_y\) が 0 のときである。
(2)停留点の評価
(極値となる十分条件)
停留点となるとテイラー展開の1次項は消え、次式が成り立つ。(3次以降と剰余項は無視する)
\(f(x,y)=f(a,b)+\frac{1}{2!}(h\pder{}{x}+k \pder{}{y})^{2} f(a,b)\)
\(=f(a,b)+\frac{1}{2}(h^2 \pdera{f}{x}+2hk\frac{\partial^2 f}{\partial y \partial x}+k^2\pdera{f}{y})\)
\(G(x,y)=f(x,y)-f(a,b)\)\(=\underline{\frac{1}{2}(h^2 f_{xx}+2hk f_{xy}+k^2 f_{yy})}\)
(\((f(a,b)\)は定数であることに留意する。)
これから f(a,b) の極値を2次方程式の判別式を利用して調べていく。
上式の右辺を以下のように式変形する
(…\(\frac{k^2}{k^2}\)を掛ける)
\(G(x,y)=\frac{1}{2}k^2 [\underline{(f_{xx} \frac{h}{k})^2 +2 f_{xy}\frac{h}{k} +f_{yy}}]\)
\(α=f_{xx},\ X=\frac{h}{k}\)\(,\ β=2 f_{xy},\ C=f_{yy}\)
また
\(K=\frac{1}{2}k^2\)とする。(Kは非負)。
\(G(X)=K [\underline{(α X^2 +βX +C}]\)
下線部を \(αx^2+βx+c\) の2次方程式とすると
\(β^2-4αC=(2 f_{xy})^2-4f_{xx}f_{yy}\)\(=4f_{xy}^2-4f_{xx}f_{yy}\)\(=4[\underline{ \ f_{xy}^2-f_{xx}f_{yy}\ }]\)
上式の下線部が
判別式 \(D\)である。
\(\color{red}{D= f_{xy}^2-f_{xx}f_{yy} }\)
【補足:判別式】
2次式方程式:
\( f(x)=αx^2+βx+c=0\)の形と考える。
\( x=\frac{β \pm \sqrt{β^2-4αc}}{2α}=\frac{β \pm \sqrt{D}}{2α} \)
\(D=\frac{1}{4}(β^2-4αc)\)
\(G(X)\)が極値をとる条件は下図の\(D\lt0\) のときである。
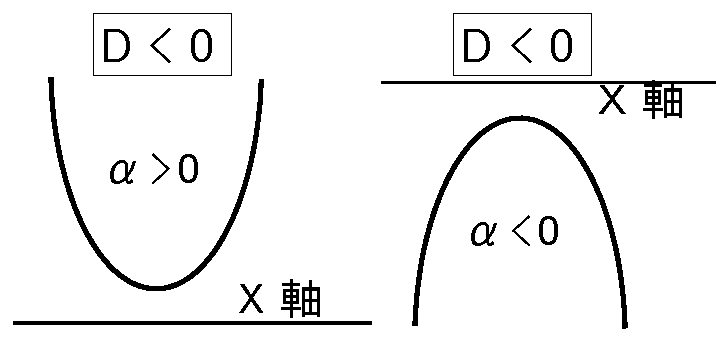
\(D\lt0\) の場合
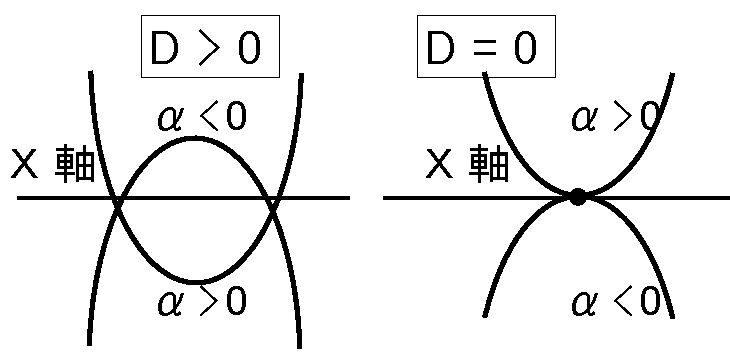
\(D\gt0,\quad \ D=0\) の場合
まとめると
\(G(x,y)=f(x,y)-f(a,b)\)\(=\frac{1}{2}k^2 [\underline{(f_{xx} \frac{h}{k})^2 +2 f_{xy}\frac{h}{k} +f_{yy}}]\)
\(G(X)=K [\underline{(α X^2 +βX +C}]\) (Kは非負)
\(D=\frac{1}{4}(β^2-4αc)=f_{xy}^2-f_{xx}f_{yy}\)
\(D\) と \(α=f_{xx}\) の符号により次のことがいえる。
・\(\color{red}{D}\) の正負から\(\color{red}{G=[f(x,y)-f(a,b)}]\) の正負 が分かる。(両者は同符号)
\(D\lt 0\)なら極値となる。 極大・極小は次の\(α(=f_{xx})\)の符号により決まる。
・\(f(a,b)\) のグラフは \(α\) が正なら下に凸、負なら下に凸である。
\(α\) が正なら極小、負なら極大である。
以上のことより
次の極値の判定方法が導かれます。
2変数関数の極値の判定方法
\(D\lt 0\)\(\ ,\ \) \(f_{xx}\gt 0\) のとき \(f(a,b)\) は極小値
\(f_{xx}=α\gt 0 \) により 下に 凸。
頂点がx軸より上にある。
(\(\because D\lt 0 ,\quad G=f(x,y)-f(a,b)\gt 0\) )
\(D\lt 0\)\(\ ,\ \) \(f_{xx}\lt 0\) のとき \(f(a,b)\) は極大値
\(f_{xx}=α\lt 0 \) により 上に 凸。
G の頂点がx軸より下にある。
(\(\because D\lt 0 ,\quad G=f(x,y)-f(a,b)\lt 0\) )
\(D\gt 0\) のときは\(f(x,y)\) は極値をとらない。
\(D\gt 0\) により G は x軸をクロスして「正と負」をとるから。
(極値をとる G は正か負のいずれかであること)
(\(\because D\gt 0 ⇒G=f(x,y)-f(a,b)=\pm \) )
\(D= 0\) のときは\(f(x,y)\) はかどうか判らない。
注:このとき一般に深く言及していないが、その都度判断していくことになる。
ヘッセ行列式(ヘッシアン)\(H(a,b)\)
\(D\)と符号が逆となる
ヘッセ行列式(ヘッシアン)\(H\)を紹介する。
\(|H(a,b)|=
\begin{vmatrix}
f_{xx} & f_{xy}\\
f_{yx} & f_{yy}
\end{vmatrix}\)
\(=f_{xx} f_{yy}-f_{xy}^2\)
\(=-D\)
判別式\(D\)の代わりに ヘッシアン\(H\)を使い判定している本もあります。
\(D=f_{xy}^2-f_{xx}f_{yy}\)
注:\(D\)とヘッシアン\(H\)の極性(正負)が逆なので注意する。
例題1
次の関数の極値を求めよ。
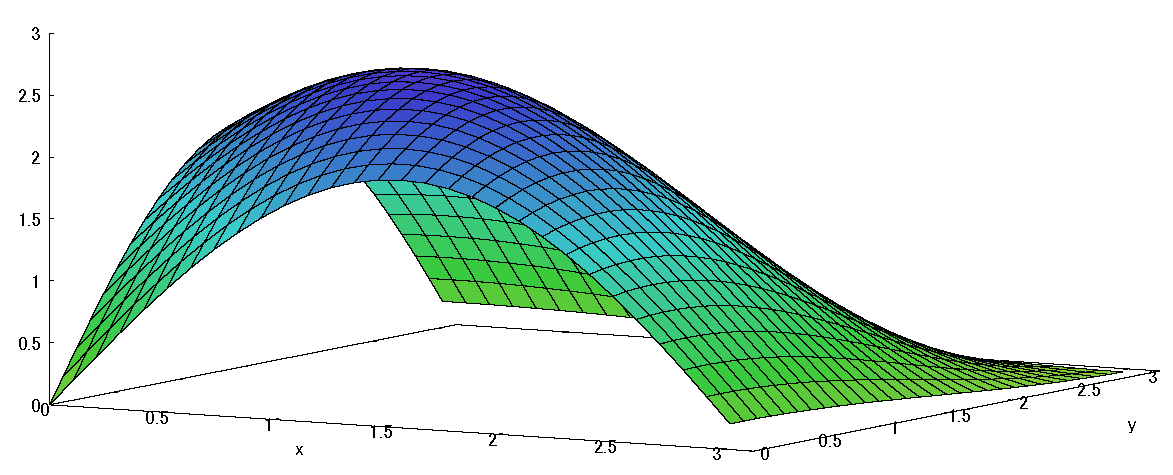
\(f(x,y)=sinx+siny+sin(x+y)\)
\( 0\lt x \lt \pi \) \(\ ,\ \) \( 0\lt y \lt \pi \)
\(f_x=cosx+cos(x+y)=0\) :ⓐ \(\ ,\ \) \(f_y=cosy+cos(x+y)=0\):ⓑ
\( (cos(x+y))'=(cos(u))'=-sinu (u)'\)\(=-sin(x+y)\cdot 1=-sin(x+y)\)
\(f_{xx}=-sinx-sin(x+y)\) \(\ ,\ \) \(f_{yy}=-siny-sin(x+y)\)
\(f_{xy}=-sin(x+y)\) \(\ ,\ \) \(f_{xy}=f_{yx}\)
(1)停留点は\(f_x=0\) と\(f_y=0\) を満たす点だから:
\(cosx+cos(x+y)=cosy+cos(x+y)=0\)
\(\therefore \) \(cosx=cosy\)
\(\therefore x=y\)…これをⓐに代入すると:
(\(cos2x=2cos^2x-1\)) 【三角関数 参照先】
\(cosx+cos2x=cosx+2cos^2x-1\)\(=\color{blue}{(2cosx-1)}\)\(\color{red}{(cosx+1)}=0 \)
\(\color{blue}{2cosx-1=0}\) \(\ → \) \(\color{blue}{cosx=\frac{1}{2}}\)
\(\ → \) \( \underline{ x=\frac{\pi}{3} \ ,\ y=\frac{\pi}{3} }\)
\(\color{red}{cosx+1=0}\) \(\ → \) \(\color{red}{cosx=-1}\)
\(\ → \) \(\underline{x=\pi \ , \ y=\pi}\)
【参考】\(cosx=cosy\):
\(cosx=cos(2\pi-x)=cosy\) \(\ → \) \(y=2\pi-x\)
\( \therefore x+y=2\pi\)
\(cosx=-cos(x+y)=-cos(2\pi)=-1\)
\(\ → \) \(x=\pi\) \(\ , \) \(y=\pi\) 上記と同じ結果を得た。
\((x,y)=(\pi,\pi)\)は極値点にはならない。(以下の(3)より)
(2)\(\underline{(x,y)= (\frac{\pi}{3},\frac{\pi}{3}) }\) について
ヘッセ行列を求める準備:
\(sinx=sin \frac{\pi}{3}=\frac{\sqrt{3}}{2}\)
\(sin(x+y)=sin(\frac{2\pi}{3})\) \(=sin(\pi-\frac{\pi}{3})=sin\frac{\pi}{3}\)\(=\frac{\sqrt{3}}{2}\)
\(cos(x+y)=cos(\frac{2\pi}{3})\)\(=-\frac{1}{2}\)
\(f_{xx}=-sinx-sin(x+y)\)\(=-\frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{2}\)\(=-\sqrt{3}\)
\(f_{yy}=-siny-sin(x+y)\)\(=-\frac{\sqrt{3}}{2}- \frac{\sqrt{3}}{2}\)\(=-\sqrt{3}\)
\(f_{xy}=-sin(x+y)\)\(=-\frac{\sqrt{3}}{2}\)
\(|H(a,b)|=
\begin{vmatrix}
f_{xx} & f_{xy}\\
f_{yx} & f_{yy}
\end{vmatrix}\)
\(=f_{xx} f_{yy}-f_{xy}^2\)
\(=(-\sqrt{3})(-\sqrt{3})-(-\frac{\sqrt{3}}{2})^2\)
\(=3-\frac{3}{4}\)\(\gt 0\)
以下より\( (\frac{\pi}{3},\frac{\pi}{3}) \) は極大点である。
・\(D=-|H(a,b)| \lt 0\)
・\(f_{xx}=-\sqrt{3} \lt 0\)
極大値は \(f (\frac{\pi}{3},\frac{\pi}{3})=\frac{3\sqrt{3}}{2}\)
\(sin\frac{\pi}{3}+sin\frac{\pi}{3}+sin\frac{2\pi}{3}\)\(=\frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{2}\)
(3)\(\underline{(x,y)= (\pi,\pi) }\) について
\(f_{xx}(\pi,\pi)=0\) \(\ , \) \(f_{yy}=(\pi,\pi)=0\)
\(f_{xy}=(\pi,\pi)=0\)
これからヘッシアンを求めると
\(|H(a,b)|=0\) となり極値の判定は別途に行うことになる。
\(|H(a,b)|=0\) による個別評価
まず判定のため、与式を式変形する。
倍角の公式 \(sin2A=2sinAcosA\) を使う。
\(f(x,y)=sinx+siny+sin(x+y)\)
\(=2sinx+sin2x\)
\(=2sinx+2sinxcosx\)
\(\therefore \underline{ f(x,y)=2sinx(1+cosx) }\)
上式においての\(x=y=\pi\) 近傍の局所的な変化を調べる。
\(x=\pi\)を外した\(\pi-ε=\pi_-\)\(\ , \)\(\pi+ε=\pi_+\) とする。
(極値点候補の前後の\((\pi \pm ε)\) について調べる)
まず、\(\pi\)近傍の\(\pi_-\) と \(\pi_+\)では \((1+cosx)\gt 0\) である。
\(\because \pi \) の前後では \(\ cosx\gt -1\)
従って、\(f\) の正負は\(sinx\)の正負により決まる。
\(f\)が\((\pi,\pi)\) で極値をとるには\(\pi\)近傍では\(sinx\)は正また負のどりらかである。
(例えば\(f(a)\)が極小(下に凸)のとき、近傍では「\(f(a\pm ε)-f(a) \gt 0\)」である)
しかし\(\pi_-\)では\(sinx\)は正、\(\pi_+\)では\(sinx\)は負と、両方があらわれる。
これより\((x,y)= (\pi,\pi)\)では極値点ではない。
fig2 \(f(x,y)=sinx+siny+sin(x+y)\)
\( 0\lt x \lt \pi \) \(\ ,\ \) \( 0\lt y \lt \pi \)
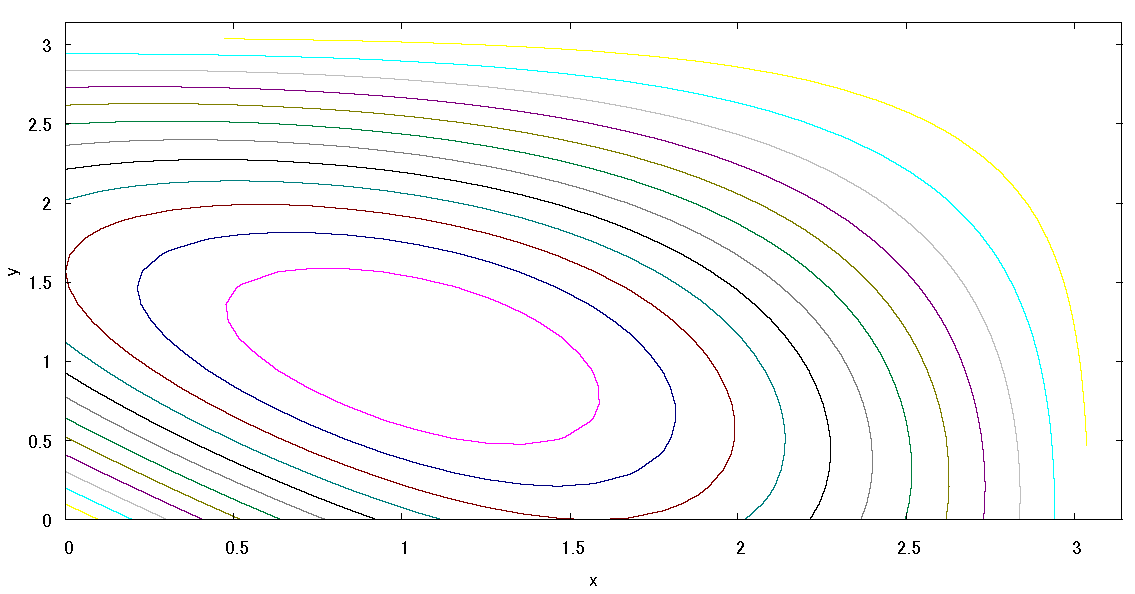
fig3 \(f(x,y)\) の等高線
領域を(\( \pi → 2\pi \))に広げると極小が現れる。
上記(1)項での \(cosx=\frac{1}{2}\) を満たす点は \(x=y=\frac{\pi}{3}\) 以外に次の極小点がある。
極小点:\(x=y=\frac{5\pi}{3}\) …下図 fig4,5 参照
\(cos(2\pi-θ)=cosθ\) \(\ ,\ \) \(\frac{5\pi}{3}=2\pi-\frac{\pi}{3} \)
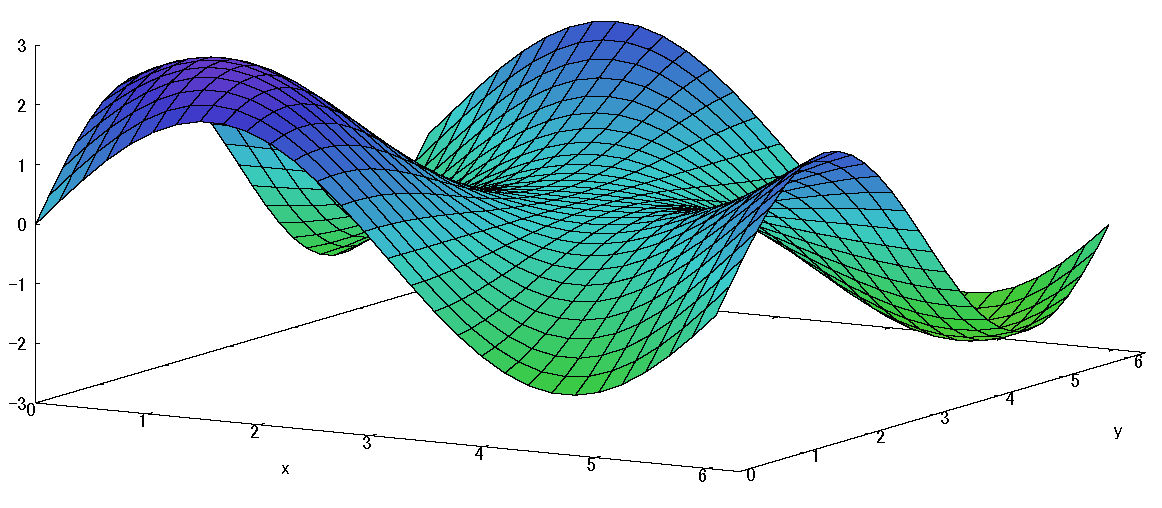
fig4 \(f(x,y)=sinx+siny+sin(x+y)\)
\( 0\lt x \lt 2\pi \) \(\ ,\ \) \( 0\lt y \lt 2\pi \)
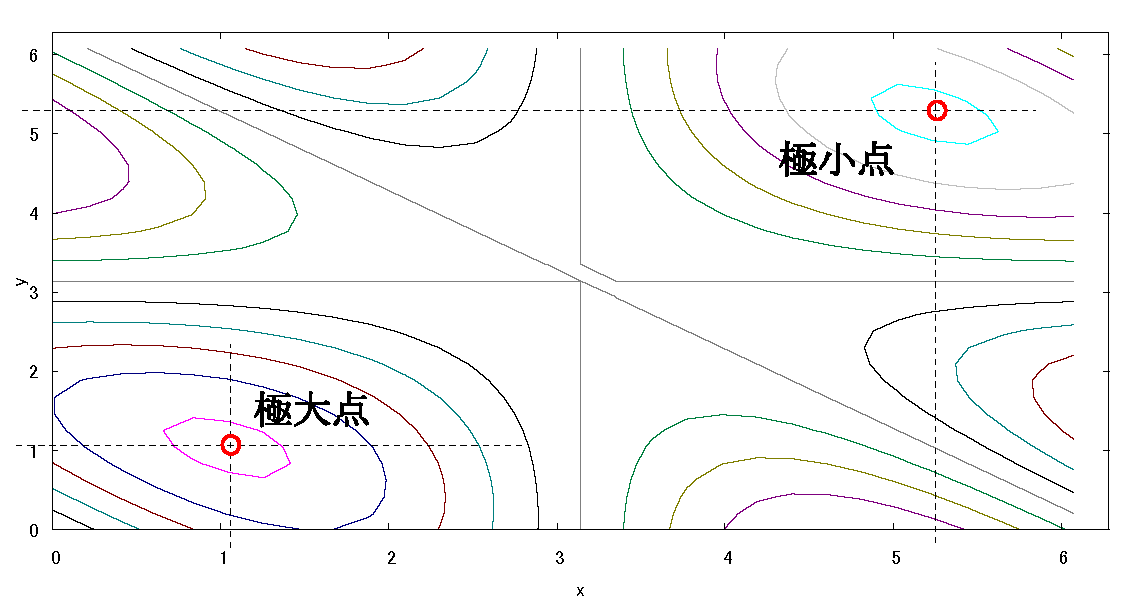
fig5 \(f(x,y)\) の等高線
例題2
次の関数の極値を求めよ。
\(f(x,y)=e^{-x^2-y^2}(2x^2+y^2)\)
簡略のため:
\(\color{red}{u=-x^2-y^2}\) \( →\) \(e^{-x^2-y^2}=e^u\) とする。
…項数が多いので注意して計算しよう…
\(\color{red}{f_x}\)
\(=-2x(2x^2+y^2)e^u+4xe^u\)
\(=(-4x^3-2xy^2+4x)e^u\)\(=\color{red}{-2x(2x^2+y^2-2)e^u}\) :ⓐ
\(\color{blue}{f_y}\)
\(=-2y(2x^2+y^2)e^u+2ye^u\)
\(=(-4x^2y-2y^3+2y)e^u\)
\(=\color{blue}{-2y(2x^2+y^2-1)e^u}\) :ⓑ
\(\color{red}{f_{xx}}\)
\(=(12x^2-2y^2+4)e^u\)\(+(-2x)(-4x^3-2xy^2+4x)e^u\)
\(=\color{red}{(8x^4-20x^2+4x^2y^2-2y^2+4)e^u}\)
\(\color{blue}{f_{yy}}\)
\(=(-4x^2-6y^2+2)e^u\)\(+(-2y)(-4x^2y-2y^3+2y)e^u\)
\(=\color{blue}{(4y^4-10y^2-4x^2+8x^2y^2+2)e^u}\)
\(\color{fuchsia}{f_{xy}}\)
\(=(-4xy)e^u+(-2y)(-4x^3-2xy^2+4x)e^u\)
\(=\color{fuchsia}{(4xy^3+8x^3y-12xy)e^u}\)
停留点の条件:\(f_x(a,b)=0,\ f_y(a,b)=0\) から停留点を求める。
以下にように式ⓐ、式ⓑの方程式を解き停留点を求める。:
(1)式ⓐ:\(-2x=0\) より \(x=0\) \(, \)式ⓑ:\(-2y=0\) より \(y=0\)
\(\ \therefore \)停留点は \((0,0)\)
\(f_{xx}(0,0)=4e^u=4e^{-(0+0)}=4\)
\(f_{yy}(0,0)=2e^u=4e^{-(0+0)}=2\)
\(f_{xy}(0,0)=0\cdot e^u=0\)
\(|H(a,b)|=
\begin{vmatrix}
f_{xx} & f_{xy}\\
f_{yx} & f_{yy}
\end{vmatrix}\)
\(=f_{xx} f_{yy}-f_{xy}^2\)
\(=4\cdot 2 -0=8\)\(\gt 0\)
( \( D=-|H| \lt 0\) )
\(\therefore (0,0)\)は極値点。
\(f_{xx} \gt 0\) より \(f(0,0)=0\) は極小値。
(2)\(x=0\) として \((2x^2+y^2-1)=0\) より \(y=\pm1\)\(⇒ \)\((0,\pm1)\)
\(f_{xx}(0,\pm1)\)\(=2e^u=2e^{-(0+1)}=2e^{-1}\)
\(f_{yy}(0,\pm1)\)\(=-4e^u=-4e^{-(0+1)}=-4e^{-1}\)
\(f_{xy}(0,\pm1)\)\(=0\cdot e^u=0\)
\(f_{xy}(0,1)=(4xy^3+8x^3y-12xy)e^u\)\(=(4+8-12)\cdot 1=0\)
\(f_{xy}(0,-1)\)\(=(-4-8+12)\cdot 1=0\)
\(|H(a,b)|=f_{xx} f_{yy}-f_{xy}^2\)
\(=\frac{2}{e}\cdot -\frac{4}{e}-0=-\frac{8}{e^2}\)\(\lt 0\)
\(\therefore (0,\pm1)\) は極値点ではない。
(参考)\(f(0,\pm1)=e^{-x^2-y^2}(2x^2+y^2)\)
\(=e^{-0-1}(0+1)\)\(=e^{-1}(1)\)\(=\frac{1}{e}\)
(3)\(y=0\) として \((2x^2+y^2-2)=0\) より \(x=\pm1\)\(⇒ \)\((\pm1,0)\)
\(f_{xx}(\pm1,0)\)\(=(20-12)e^u=-8e^{-1}=\frac{-8}{e}\)
\(f_{yy}(\pm1,0)\)\(=(-4+2)e^u=-2e^{-1}=\frac{-2}{e}\)
\(f_{xy}(\pm1,0)\)\(=0\cdot e^u=0\)
\(|H(a,b)|=f_{xx} f_{yy}-f_{xy}^2\)
\(=\frac{-8}{e} \frac{-2}{e}-0=\frac{16}{e^2}\)\(\gt 0\)
\(\therefore (\pm1,0)\) は極値点 ⇒\((1,0) (-1,0)\)の2点である。
\(f_{xx} \lt 0\) より \(f(\pm1,0)=\frac{2}{e}\)は極大値
\(f(\pm1,0)=e^{-x^2-y^2}(2x^2+y^2)\)
\(=e^{-1-0}(2+0)\)\(=e^{-1}(2)\)\(=\frac{2}{e}\)
(4)\((2x^2+y^2-2)=0\) と \((2x^2+y^2-1)=0\)を解く。
両式の連立方程式を解くと、矛盾の結果 \(-1=0\) となり、
停留点は得られない。
・極小点\((0,0)\)、極小値 \(f(0,0)=0\)
・極大点\((1,0),(-1,0)\)、 極大値\(f(\pm 1,0)=\frac{2}{e}\)
下の等高線図から極値点が3つあるのが確認できる。
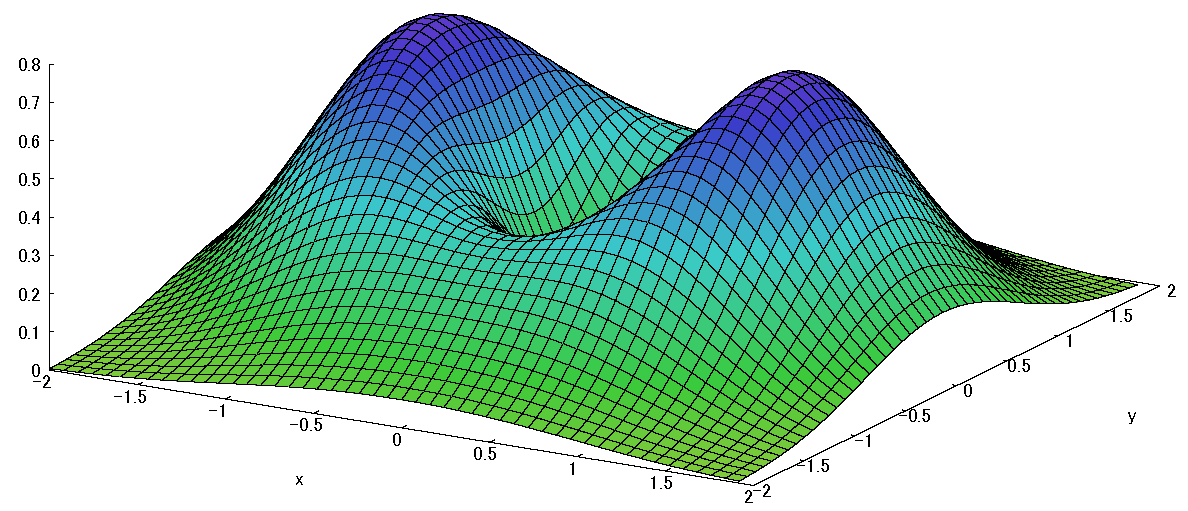
fig6 \(f(x,y)=f(x,y)=e^{-x^2-y^2}(2x^2+y^2)\)
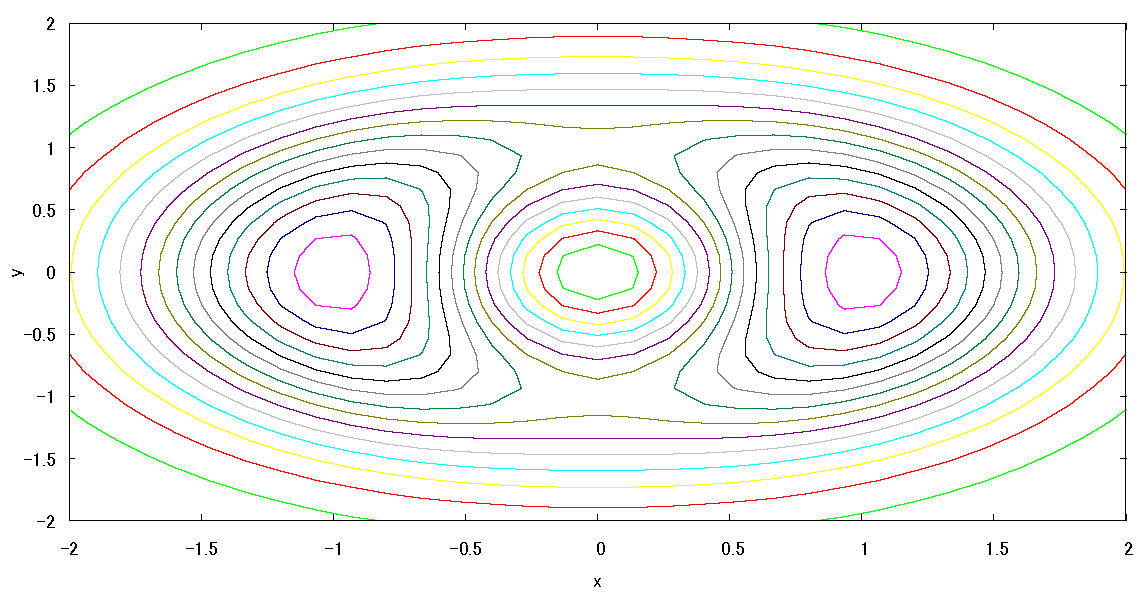
fig7 \(f(x,y)\) の等高線
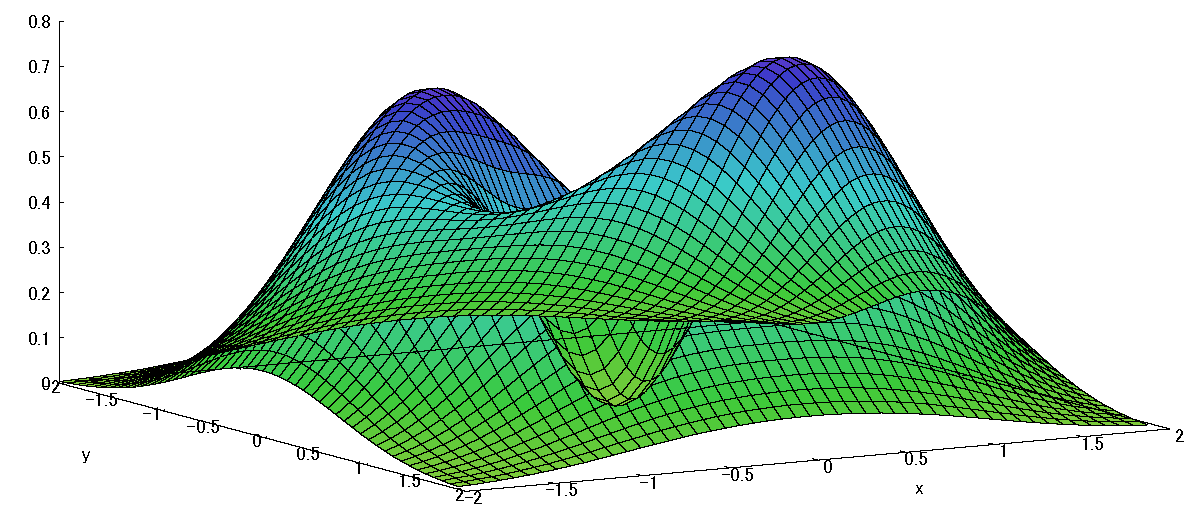
fig8 下から見た図(谷の様子が見える)
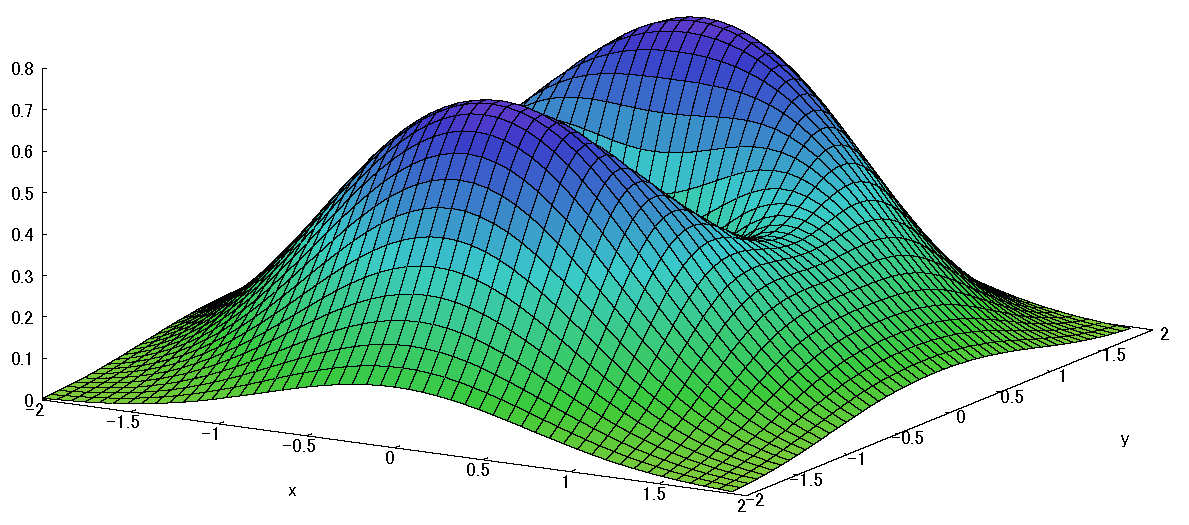
fig9 (参考)\(f(x,y)=f(x,y)=e^{-x^2-y^2}(x^2+\color{red}{2y^2})\)
x=0 線の上に山が2つ現れる