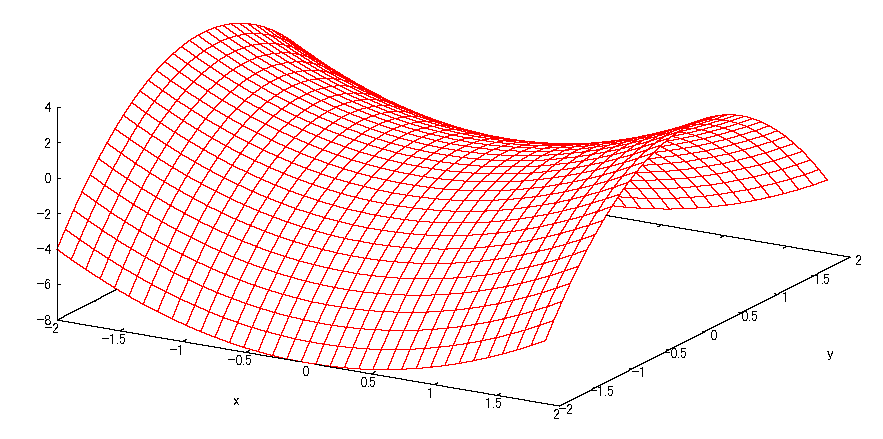
\(F(x,y)=x^2+2xy+y^2\)
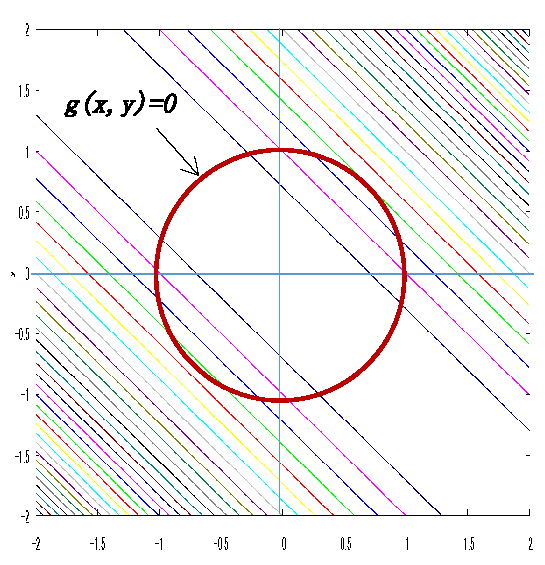
\(g(x,y)=x^2+y^2-1=0\)
\(F(x,y)=x y\)
\(g(x,y)=x^2+4y^2-4=0\)
\(f_x(a,b)-λg_x(a,b)=0\) :❶
\(f_y(a,b)-λg_y(a,b)=0\) :❷
\(f_x(a,b)=λg_x(a,b)\) :❶’
\(f_y(a,b)=λg_y(a,b)\) :❷'
\(F_x(a,b,λ)=f_x(a,b)-λg_x(a,b)=0\) :❸
\(F_y(a,b,λ)=f_y(a,b)-λg_y(a,b)=0\) :❹
\(F_λ(a,b,λ)=-g(a,b)=0\) :❺
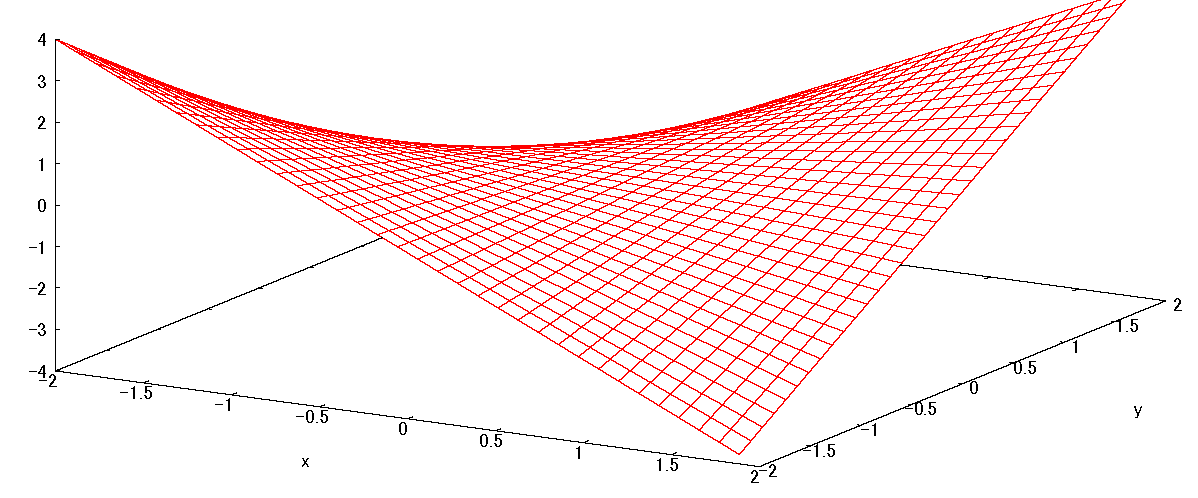
・fig1 は目的関数 \(f\) の立体図
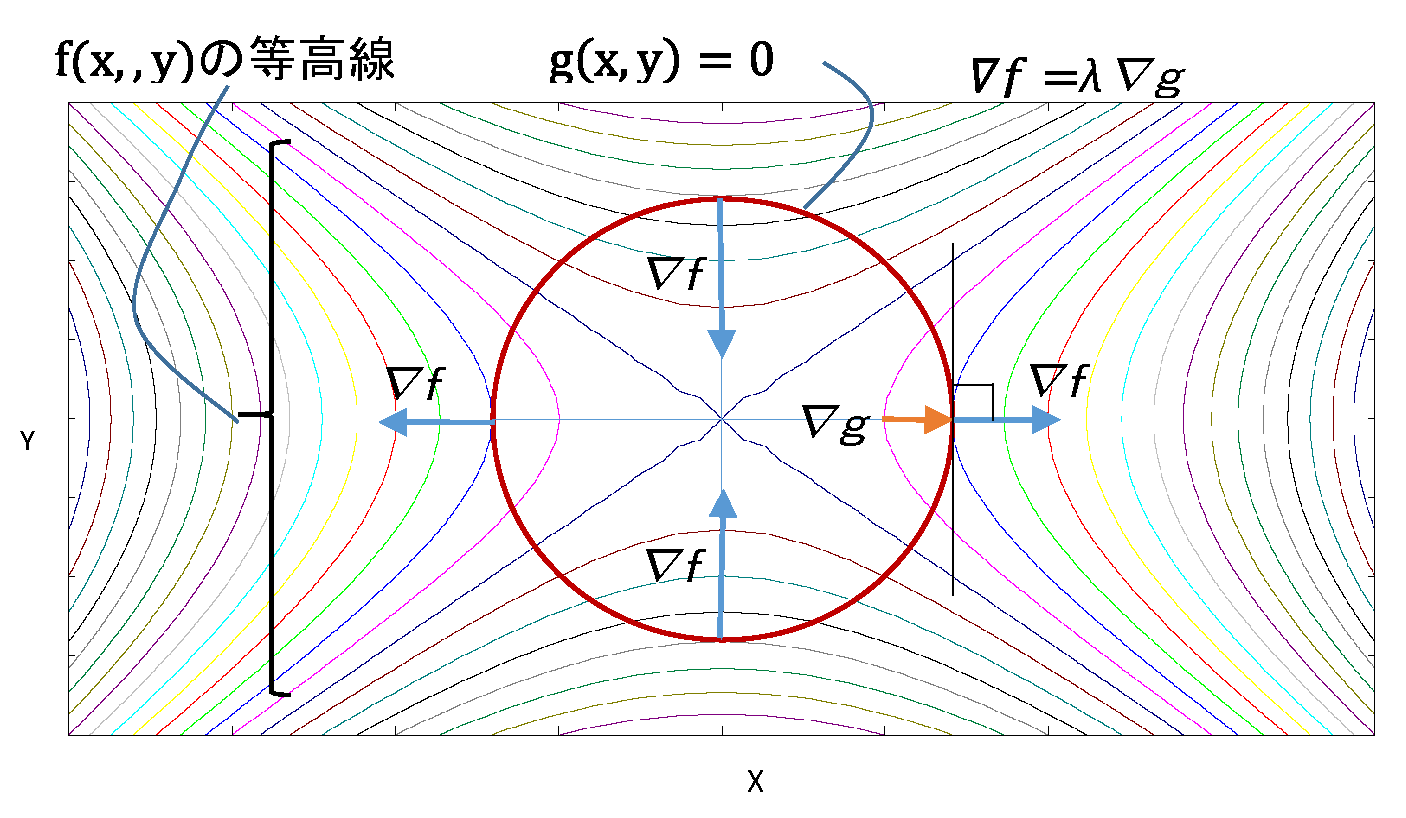
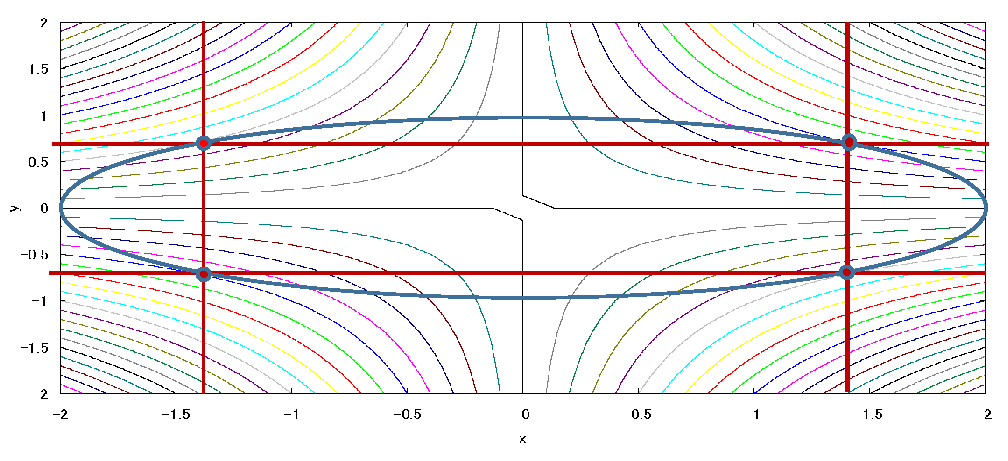
・fig2 は真上から見た \(f\) の等高線と制約条件の式 \(g\) の曲線
\(f_x(a,b)=λg_x(a,b)\) :❶’ \(f_y(a,b)=λg_y(a,b)\) :❷'
\(\nabla \bv{f} =\color{red}{ λ }\nabla \bv{g} \) (式❶’ ❷'をまとめた式)\(\varphi(a)=b \) → \( f(a,b)=f(a,\varphi(a) )\)
\(g(x,y)\) はx,y の陰関数、\(g_x(a,b)\ne 0\) または\(g_y(a,b)\ne 0\) とする。
\(g_x=\pder{g}{x}(x,\varphi(x))\) \(\ ,\ \) \(g_y=\pder{g}{y}(x,\varphi(x))\)
\(\frac{dy}{dx}=\frac{d\varphi(x)}{dx}=(\color{red}{\varphi(x))'}\)
\(=\color{red}{ -\frac{g_x(x,\varphi(x))}{g_y(x,\varphi(x))} }\)
\(\underline{\frac{d}{dx}(f(x,\varphi(x))}=0\) \(\quad (y=\varphi(x))\)
合成関数の連鎖律をつかい展開する
\(=\pder{f}{x} \der{x}{x}\)\(+\pder{f}{y} \der{\varphi}{x}\)
\(=\pder{f}{x}\)\(+\pder{f}{y} (\varphi(x))'\)
\( (\varphi(x))'\)に上記の結果を代入
\(=\pder{f}{x}-\pder{f}{y} \color{red}{\frac{g_x(x,\varphi(x))}{g_y(x,\varphi(x))} }\)
\(=f_x-f_y \frac{g_x(x,\varphi(x))}{g_y(x,\varphi(x))} \)
変数を換える:\((x,y)→(a,\varphi(x)) →(a,b)\)
\(\underline{ =f_x(a,b)-f_y(a,b)\frac{g_x(a,b)}{g_y(a,b)} }\)
\(λ=\frac{f_y(a,b)}{g_y(a,b)}\)とすると:
\(f_x(a,b)-λ g_x(a,b)=0\) :❶
同様にして:
\(f_y(a,b)-λ g_y(a,b)=0\) :❷
式❶、❷ をベクトル表示すると:
\( \nabla \bv{f}- λ \nabla \bv{g}=0\) \(\ ⇒\ \) \( \nabla \bv{f}= λ \nabla \bv{g}\)
\(\pder{F}{x}(a,b,λ)\)\(=\pder{f}{x}(a,b,λ)-λ\pder{g}{x}(a,b)=0\) :❸
\(\pder{F}{y}(a,b,λ)\)\(=\pder{f}{y}(a,b,λ)-λ\pder{g}{y}(a,b)=0\) :❹
\(\pder{F}{λ}(a,b,λ)\)\(=-g(a,b)=0\) :❺
式❶❷の証明中の式を以下のように式変形する。
( \((a,b)\)を省略して表記する)
\(f_x=f_y \frac{g_x}{g_y}\)
\( \rightarrow \)
\(\color{red}{ \frac{f_x}{g_x}=\frac{f_y}{g_y} }=λ\) :❻
\( \color{red}{
\begin{vmatrix}
f_{x} & g_{x}\\
f_{y} & g_{y}
\end{vmatrix}
}\)
\(=f_x g_y-f_y g_x=0 \) :❼
例題1 は本式を使って解答した。
\(g(x,y)=x^2+(-x)^2-1=0\) \(\ \rightarrow \ \) \(2x^2=1\) \(\ \rightarrow \ \)
\(x=\pm \frac{1}{\sqrt{2}}=\pm \frac{\sqrt{2}}{2}\)
\(y=-x=-( \pm\frac{\sqrt{2}}{2} ) \) \(=\mp \frac{\sqrt{2}}{2} \)
\(\underline{ (x,y)=( \pm \frac{\sqrt{2}}{2} , \mp \frac{\sqrt{2}}{2} ) }\)
(複号同順)
\(g(x,y)=x^2+(x)^2-1=0\) \(\ \rightarrow \ \) \(2x^2=1\) \(\ \rightarrow \ \)
\(x=\pm \frac{1}{\sqrt{2}}=\pm \frac{\sqrt{2}}{2}\)
\( y=x=\pm \frac{\sqrt{2}}{2} \)
\(\underline{ (x,y)=( \pm \frac{\sqrt{2}}{2} , \pm \frac{\sqrt{2}}{2} ) }\)
(複号同順)
極大値:\(f(xy)=2\)
極大点:\((x,y)=\)\(( \pm \frac{\sqrt{2}}{2} , \pm \frac{\sqrt{2}}{2} )\)
(複号同順)
注:極大点は第1、第3 の象限にある。
極小値:\(f(x,y)=0\)
極小点:\((x,y)=\)\(( \pm \frac{\sqrt{2}}{2} , \mp \frac{\sqrt{2}}{2} )\)
(複号同順)
注:極小点は第2、第4 の象限にある。
条件式を変形すると(各項を4で割る)
\(\frac{x^2}{2^2}+\frac{y^2}{1^2}=1\)
楕円の式です:長軸\(2a=4\) ,短軸\(2b=2\)
\(y=2λx\) :ⓐ \(\ ,\ \) \(x=8λy\) :ⓑ
\(x=8λy=8λ(2λx)=16λ^2x\)
\(16λ^2x-x=0\)\(\ ,\ \) \(x(16λ^2-1)=0\)
\(\color{blue}{x=0}\)\(\ または\ \) \(\color{teal}{ λ=\pm \frac{1}{4} }\)
\(y=2λx=0\) \(\ より\ \) \((x,y)=(0,0)\) であり、これは
\(g=0\)を満足せず。
これより\(x=0\) は対象から除外する。
\(y=2λx=2\cdot \frac{1}{4}\cdot x=\frac{1}{2}x\)
\(g=x^2+4(\frac{1}{2}x)^2-4=2x^2-4=0\) \(\ \ \)
\(\therefore x=\pm \sqrt{2}\)
\(y=\frac{1}{2}x=\frac{1}{2}\cdot (\pm \sqrt{2}) \)\(=\pm \frac{\sqrt{2}}{2}\)
\(\therefore \color{red}{(x,y)=(\pm \sqrt{2},\pm \frac{\sqrt{2}}{2})}\)
\(y=2λx=2\cdot -\frac{1}{4}\cdot x=-\frac{1}{2}x\)
\(g=x^2+4(-\frac{1}{2}x)^2-4=2x^2-1=0\) \(\ \ \)
\(\therefore x=\pm \sqrt{2}\)
\(y=2λx=2\cdot -\frac{1}{4}\cdot x=-\frac{1}{2}\cdot (\pm \sqrt{2}) \)\(=\mp \frac{\sqrt{2}}{2}\)
\(\therefore \color{red}{(x,y)=(\pm \sqrt{2},\mp \frac{\sqrt{2}}{2})}\)
\(f\ (\pm \sqrt{2}, \pm \frac{\sqrt{2}}{2})\) \(=xy\) \(=\pm \sqrt{2}\cdot \pm \frac{\sqrt{2}}{2}\)\(=1\)
\(f\ (\pm \sqrt{2},\mp \frac{\sqrt{2}}{2})\) \(=xy\)\(= \pm \sqrt{2} \cdot \mp \frac{\sqrt{2}}{2} \)
\(= -\frac{2}{2}=-1\)
\(\begin{cases}
極大値& f(xy)=1 \\
極大点& (\pm \sqrt{2},\pm \frac{\sqrt{2}}{2})(複号同順)
\end{cases}\)
\(\begin{cases}
極小値& f(xy)=-1 \\
極小点& (\pm \sqrt{2},\mp \frac{\sqrt{2}}{2})(複号同順)
\end{cases}\)
・\(H \gt 0\) :(a,b)において極大である。
・\(H \lt 0\) :(a,b)において極小である。
・\(H = 0\) :(a,b)での極値については不明。
\(F_{xx}=-2λ=-\frac{1}{2}\) \(\ ,\ \)\(F_{yy}=-8λ=-2\)
\(F_{xy}=F_{yx}=1\) \(\ ,\ \) \(g_x=2x=2 \sqrt{2}\) \(\ ,\ \) \(g_y=8y=8\frac{\sqrt{2}}{2}=4\sqrt{2}\)
これを行列式に代入:
\(H=
\begin{vmatrix}
0& 2\sqrt{2} & 4\sqrt{2} \\
2\sqrt{2}& -\frac{1}{2} & 1\\
4\sqrt{2}& 1 & -2
\end{vmatrix}\)
\(=16+16+16+16=64 \gt 0\) (※)
\(g_x=2x=2(-\sqrt{2})=-2\sqrt{2}\) \(\ ,\ \) \(g_y=8y=8(-\frac{\sqrt{2}}{2})=-4\sqrt{2}\)
\(H=
\begin{vmatrix}
0& -2\sqrt{2} & -4\sqrt{2} \\
-2\sqrt{2}& -\frac{1}{2} & 1\\
-4\sqrt{2}& 1 & -2
\end{vmatrix}\)
\(=16+16+16+16=64 \gt 0\)
\(F_{xx}=-2λ=\frac{1}{2}\) \(\ ,\ \)\(F_{yy}=-8λ=2\)
\(F_{xy}=F_{yx}=1\) \(\ ,\ \) \(g_x=2x=2\sqrt{2}\) \(\ ,\ \) \(g_y=8y=8(-\frac{\sqrt{2}}{2})=-4\sqrt{2}\)
\(H=
\begin{vmatrix}
0& 2\sqrt{2} & -4\sqrt{2} \\
2\sqrt{2}& \frac{1}{2} & 1\\
-4\sqrt{2}& 1 & 2
\end{vmatrix}\)
\(=-16-16-16-16=-64 \lt 0\)
\(g_x=2x=-2\sqrt{2}\) \(\ ,\ \) \(g_y=8y=8(\frac{\sqrt{2}}{2})=4\sqrt{2}\)
\(H=
\begin{vmatrix}
0& -2\sqrt{2} & 4\sqrt{2} \\
-2\sqrt{2}& \frac{1}{2} & 1\\
4\sqrt{2}& 1 & 2
\end{vmatrix}\)
\(=-16-16-16-16=-64 \lt 0\)
\( F_x=y-λ\) \(\ ,\ \) \( F_y=x-λ\)
\( g_x=1\) \(\ ,\ \) \( g_y=1\)
\(\begin{vmatrix}
F_{x} & g_{x}\\
F_{y} & g_{y}
\end{vmatrix}\)
\(=f_x g_y-f_y g_x\)\(=(y-λ)\cdot 1-(x-λ)\dot 1\)\(=y-x=0\)
これを集合の記号を使い次の表し方もある:
\(\{(x,y)|x,y \ge 0,\ g=x+y-L \}\)
の有界閉集合上において連続な関数は\(f=xy\) は最大値/最小値をもつ。

1814年頃ジョージ・スチーブンソン/英 蒸気機関車の実用化
1831年頃マイケル・ファラデー/英 電磁誘導の発見
1840年 アヘン戦争
1853年 日本は米国のマシュー・ペリーから開国を迫れる。