楽しく学ぶ…線形代数
行列式と置換
(determinant and permutation)
--目 次--
1.連立1次方程式と行列式
2.3次行列式
∗サラスの式
3.列順による行列式
4.転置行列式
1.連立1次方程式と行列式
\(\begin{eqnarray}
\left\{
\begin{array}{l}
a_{11}x_1+a_{12}x_2=b_1\ (1)\\
a_{21}x_1+a_{22}x_2=b_2\ (2)
\end{array}
\right.
\end{eqnarray} \)
加減法により
\(x_2\)を消去するため(1)に\(a_{22}\)、(2)に\(a_{12}\)を掛けると、
\(x_1\)が求まる。
\(x_1=\frac{b_1 a_{22}-b_2 a_{12}}{a_{11}a_{22} - a_{12}a_{21}} \ (3) \)
\(x_1\)を消去するため(1)に\(a_{21}\)、(2)に\(a_{11}\)を掛けると、
\(x_2\)が求まる。
\(x_2=\frac{b_2 a_{11}-b_1 a_{21}}{a_{11}a_{22} - a_{12}a_{21}} \ (4) \)
この分母は\(x_1\), \(x_2\)に共通であり、以下のように高校で学んだ行列式になります。
正方行列の行列式A(determinant)の表し方次の3通りあります。
\(
\begin{eqnarray}
\mathrm{ det }A
= | A |
= \begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix}
\end{eqnarray}
\)
これをサラスの公式で解くと:
\( \quad =a_{11}a_{22} - a_{12}a_{21}\)
(3),(4)を行列式で表します。
\(x_1=
\frac{
\begin{eqnarray}
\begin{vmatrix} b_1 & a_{12} \\ b_2 & a_{22} \end{vmatrix}
\end{eqnarray} }
{\begin{eqnarray}
\begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix}
\end{eqnarray} }
, \)
\(x_2=
\frac{
\begin{eqnarray}
\begin{vmatrix} a_{11} & b_1 \\ a_{21} & b_1 \end{vmatrix}
\end{eqnarray} }
{\begin{eqnarray}
\begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix}
\end{eqnarray} }
\)
2.
3次行列式
3次の正方行列の行列式:
\(|A|=
\begin{vmatrix}
a_{1\ 1}&a_{1\ 2}&a_{1\ 3}\\
a_{2\ 1}&a_{2\ 2}&a_{2\ 3}\\
a_{3\ 1}&a_{3\ 2}&a_{3\ 3}
\end{vmatrix}
\cdots (5) \)
\( = +a_{1\ 1} a_{2\ 2} a_{3\ 3}\)
\(+a_{1\ 2} a_{2\ 3} a_{3\ 1}\)
\(+a_{1\ 3} a_{2\ 1} a_{3\ 2}\)
\(-a_{1\ 1} a_{2\ 3} a_{3\ 2}\)
\(-a_{1\ 2} a_{2\ 1} a_{3\ 3}\)
\(-a_{1\ 3} a_{2\ 2} a_{3\ 1}
\cdots (5') \)
(サラスの公式により求まる)
先に進む前に、今回、使う置換の式を記載しておきます。
\( S_3\)(3次の置換の集合)の置換の式
下段は置換の符号sgnです。
\(n=3\) すなわち3個の置換の集合(3次の置換の集合)は
\( S_3=\{σ_1,σ_2,σ_3,σ_4,σ_5,σ_6\} \)
です。
3次の行列式を
\(S_3\)
の置換とsgn を使い表わします。
これが3次の正方行列の定義式になります。
\(\underline {det|A|}= \)
\( \underline{\displaystyle \sum_{i=1}^{6} sgn(σ_ \ i \ ) \ a_{1 \ σi(1)} \ a_{2 \ σi(2)} \ a_{3 \ σi(1)}} \)\(\cdots (6) \)
上式の説明:
・成分
\(a_{\ i\ j}\)
:i=行 、j=列σ(k)
・i =2 のとき sgn(σ_2)=-1
・\(σ_2\)の置換は(上記から)
σ(1)=1, σ(2)=3, σ(3)=2となる
式(6)を以下に展開します。
\(= sgn(σ_ \ 1 \ ) \ a_{1 \ σ_1(1)} \ a_{2 \ σ_1(2)} \ a_{3 \ σ_1(3)} \)
\(\qquad = +a_{1\ 1} \ a_{2\ 2} \ a_{3\ 3} \)
\(+ sgn(σ_ \ 2 \ ) \ a_{1 \ σ2(1)} \ a_{2 \ σ2(2)} \ a_{3 \ σ2(3)} \)
\(\qquad = -a_{1\ 1} \ a_{2\ 3} \ a_{3\ 2} \)
\(+ sgn(σ_ \ 3 \ ) \ a_{1 \ σ3(1)} \ a_{2 \ σ3(2)} \ a_{3 \ σ3(3)} \)
\(\qquad = -a_{1\ 2} \ a_{2\ 1} \ a_{3\ 3} \)
\(+ sgn(σ_ \ 4 \ ) \ a_{1 \ σ4(1)} \ a_{2 \ σ4(2)} \ a_{3 \ σ4(3)} \)
\(\qquad = +a_{1\ 2} \ a_{2\ 3} \ a_{3\ 1} \)
\(+ sgn(σ_ \ 5\ ) \ a_{1 \ σ5(1)} \ a_{2 \ σ5(2)} \ a_{3 \ σ5(3)} \)
\(\qquad = +a_{1\ 3} \ a_{2\ 1} \ a_{3\ 2} \)
\(+ sgn(σ_ \ 6 \ ) \ a_{1 \ σ6(1)} \ a_{2 \ σ6(2)} \ a_{3 \ σ6(3)} \)
\(\qquad = -a_{1\ 3} \ a_{2\ 2} \ a_{3\ 1} \)
結果は行列式(5)の展開した式(5')と同じになりました。
式(6)の\(Σ\)の置換計算を展開して得た結果とサラスの公式から得た結果\((5')\)が同じであることが確認できました。
【参考】式(6)を総乗記号∏を用いて次のように書くこともあります。
総和はシグマ∑記号、掛け合わせはパイ∏記号を使います。
いずれも簡略化のために使います。(数学的な縮約ですね!)
\( \displaystyle \sum_{i=1}^{6} sgn(σ_ \ i ) \)
\(\displaystyle \prod_{ j = 1 }^3 \ a_{j \ σi(j)} \)
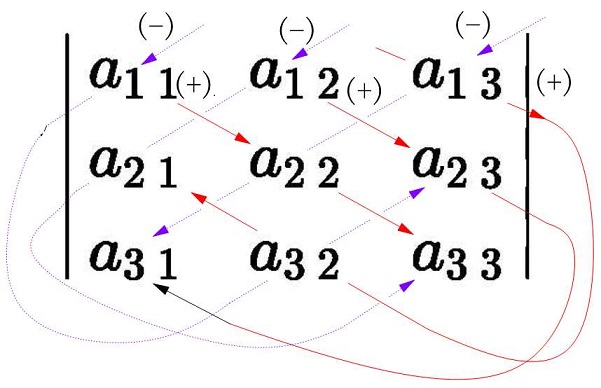
3.列順による行列式
今までは行の順により行列を表現しました。(それが式(6)です)
「列順による行列式」とは転置(行と列を入れ換えた行列)が背景にあります。
以下の3つの式は同じ行列式を表しています。
式(7)、(8)は列順に表しています。
\(a_{i j} = a_{行\ 列} \)
行の順に並ぶとは:
\( a_{\color{red}1 \ σ_i(1)}\ a_{\color{red}2 \ σ_i(2)}\ a_{\color{red}3 \ σ_i(3)\ } \)
列の順に並ぶとは:
\( a_{σ_i(1)\ \color{red}1 }\ a_{σ_i(2)\ \color{red}2 }\ a_{σ_i(3)\ \color{red}3 } \)
\(det|A| \)
\(= \displaystyle \sum_{i=1}^{6} sgn(σ_ \ i \ ) \ a_{\ 1 \ σi(1)} \ a_{\ 2 \ σi(2)} \ a_{\ 3 \ σi(1)} \)
\( \cdots (6) \)
\(= \displaystyle \sum_{i=1}^{6} sgn(σ^{-i} \ ) \ a_{\ σi^{-1}(1)\ 1} \ a_{\ σi^{-1}(2)\ 2} \ a_{\ σi^{-1}\ 3}\)
\( \cdots (7) \)
\(= \displaystyle \sum_{i=1}^{6} sgn(σ_ \ i \ ) \ a_{ σi(1)\ 1} \ a_{\ σi(2)\ 2} \ a_{\ σi(3)\ 3} \)
\( \cdots (8) \)
この3つの式が等しくなることを確認しましょう。
(行順(式(6))と列順(式(8))の行列式は同じ)
添字が沢山あり、分かりにくいと思いますが辛抱して下さい。
ここでは、例として\(S_3\)の置換\(σ_5\)による行列式を計算します。
\(\sigma_5=
\begin{pmatrix}
1 & 2 & 3 \\
3 & 1 & 2
\end{pmatrix}\)
\( (σ_5)^{-1}=
\begin{pmatrix}
1 & 2 & 3 \\
2 & 3 & 1
\end{pmatrix}=σ_4\)
\(sgn(σ_5)=sgn({σ_5}^{-1})=-1 \)
\(sgn(σ_5) a_{\color{red}1 \ σ_5(1)}\ a_{\color{red}2 \ σ_5(2)}\ a_{\color{red}3 \ σ_5(3)\ } \)
\(=sgn(σ_5) a_{\ \color{red}1 \ 3}\ a_{\ \color{red}2 \ 1}\ a_{\ \color{red}3 \ 2 } \)
\(=sgn(σ_5) a_{\ 2 \ 1}\ a_{\ 3 \ 2 }\ a_{\ 1 \ 3} \)
(上式の成分\(a\)の配置を変えた)
\(=sgn({σ_5^{-1}}) a_{\ σ^{-1}(1) \ 1}\ a_{\ σ^{-1}(2)\ 2 }\ a_{\ σ^{-1}(3) \ 3} \)
(上式を逆置換で表した)
\(σ_5\)以外でも同様であり、式(6),(7),(8)が等しいことが確認できました。
ここで見方を変えて考えると:
\(σ(i)=j\) の逆置換は \(σ^{-1}(j)=i \ \) です。
置換の\(i\)が1~3に対し\(j\)も1~3 に変わる。
(逆置換は元の置換と組み合わせ同じです)
\(σ_5\)において以下の式を置換計算し、右辺に結果を書くと:
\(a_{1\ σ(1)}\ a_{2\ σ(2)}\ a_{3\ σ(3)} = a_{1\ 3\ } a_{2\ 1\ } a_{3\ 2} \)
\(a_{\ σ^{1}(1)\ 1\ } a_{\ σ^{1}(2)\ 2\ } a_{\ σ^{1}(3)\ 3\ } = a_{2\ 1\ } a_{3\ 2\ } a_{1\ 3} \)
\(a_{i j}\)の並び順は違うが、(成分\(a\)の配置が違う)、上の2つの式は同じです。
見方を変えても式(6),(7),(8)が等しいことが分かりました。
4.転置行列式
転置は行列式\(|A|\)の行と列を入れ換えた行列式、\(|{}^{t}A|\)で表す。
\(|A|=
\begin{vmatrix}
a_{1\ 1}&a_{1\ 2}&a_{1\ 3}\\
a_{2\ 1}&a_{2\ 2}&a_{2\ 3}\\
a_{3\ 1}&a_{3\ 2}&a_{3\ 3}
\end{vmatrix}\)
\(|{}^{t}A|=
\begin{vmatrix}
a_{1\ 1}&a_{2\ 1}&a_{3\ 1}\\
a_{1\ 2}&a_{2\ 2}&a_{3\ 2}\\
a_{1\ 3}&a_{2\ 3}&a_{3\ 3}
\end{vmatrix}
\)
ここで
\(|{}^{t}A|=
\begin{vmatrix}
c_{1\ 1}&c_{1\ 2}&c_{1\ 3}\\
c_{2\ 1}&c_{2\ 2}&c_{2\ 3}\\
c_{3\ 1}&c_{3\ 2}&c_{3\ 3}
\end{vmatrix}\)
とおく。
まず:
①\(c_{\ i\ j} = a_{\ j\ i} \)
次に行列式の定義式(6)と同様に次式が書ける。
②
\( |{}^{t}A|=
\displaystyle \sum_{i=1}^{6} sgn(σ_ \ i \ ) \ c_{1 \ σi(1)} \ c_{2 \ σi(2)} \ c_{3 \ σi(1)} \)
\(i\)と\(j\)の入れ換えだから(\(c_{\ i\ j} = a_{\ j\ i}\))、上式を次のように書ける。
③
\( |{}^{t}A|=
\displaystyle \sum_{i=1}^{6} sgn(σ_ \ i \ ) \ a_{σi(1)\ 1} \ a_{σi(2)\ σi(2)} \ a_{σi(1)\ 3} \)
これは行列式\(|A|\) の定義式そのものである。
\( \therefore \quad |A|=|{}^{t}A| \)
すなわち行列式は転置しても変わらない。
最後に一言:
・行列式は正方行列において定義されます。
・転置は正方行列でなくても定義できます。