\(f'(x)=3x^2-12=3(x^2-4)=3(x+2)(x-2)\)
\( f'(x)=0 \)
に対し \( x=-2, \ x=2 \)
…
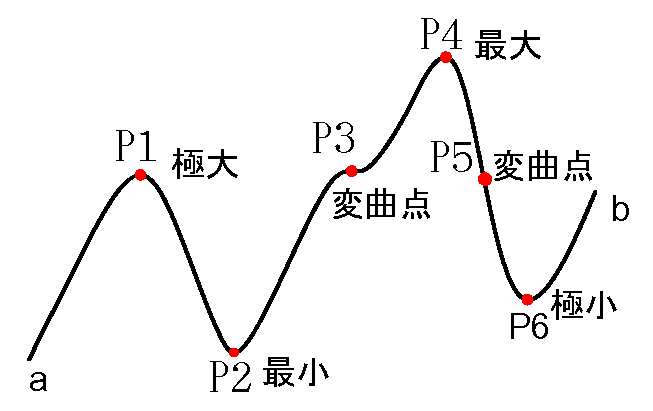
極値候補の位置
\(f(-2)=21 ,\) \(\ f(2)=-11\)
…
極小、極大の候補
二回微分を求める
(変曲点などの解析)
\(f''(x)=6x\)
\( f''(x)=0 \)
に対し \( x=0 \)
…
変曲点候補の位置
\( f(0)=5 \)
…
変曲点候補の値
❶ \(f(x)=x^3-12x+5 \)
❷
\(f'(x)=3(x^2-4)\)
❸ \(f''(x)=6x\)
各極値候補 x=-2, 0, 2 の前後に対し、式 ❷、❸ の「正か負」を調べる。
(例えばx=2に対し x<2, x>2 のときの極性を調べる)
\( \begin{array}{c|c|c|c|c|c|c|c}
\hline
x & \cdots & -2 & \cdots & 0 & \cdots & 2 & \cdots \\
\hline
f'(x) & + & 0 & - & - & + & + & + \\
\hline
f''(x) & - & - & - & 0 & + & + & + \\
\hline
f(x) & \nearrow & 極大 & \searrow & 変曲点 & \searrow & 極小 & \nearrow \\
\hline
\end{array}
\)
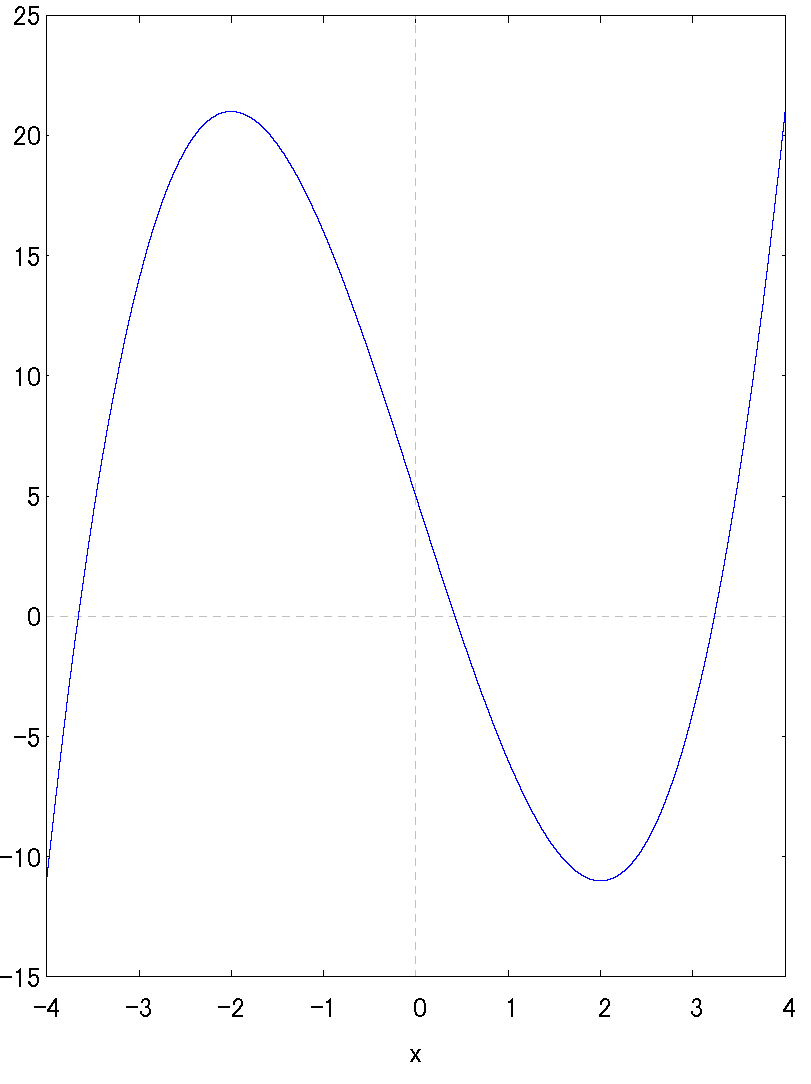
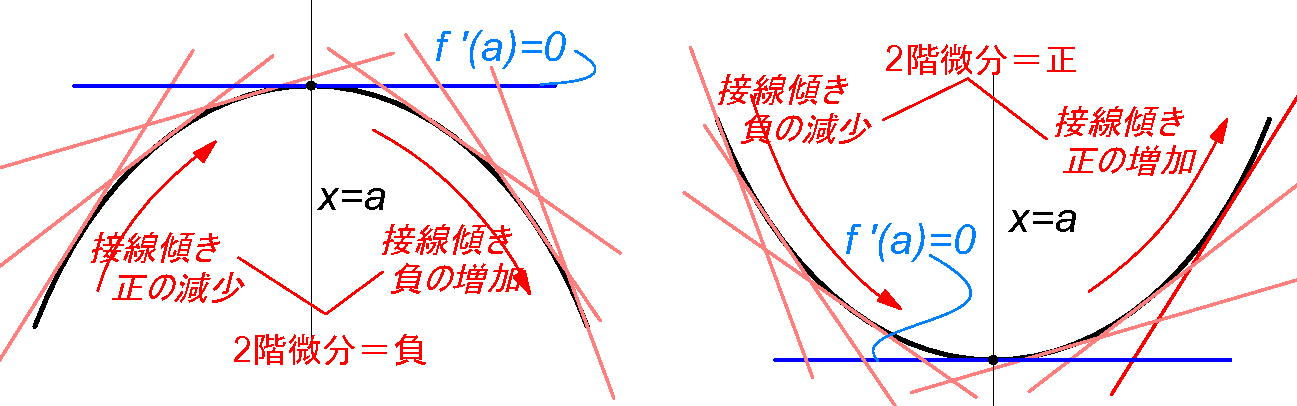
f ' , f '' の符号、変化の状況の結果から、上述した候補通り、極大、極小、変曲点となりました。
すなわち 極大点=(-2,21), 極小点=(2,-11), 変曲点=(0,5)
特に変曲点候補の前後ではf 'の符号(接線の傾き)が変ったので変曲点と判断できる。

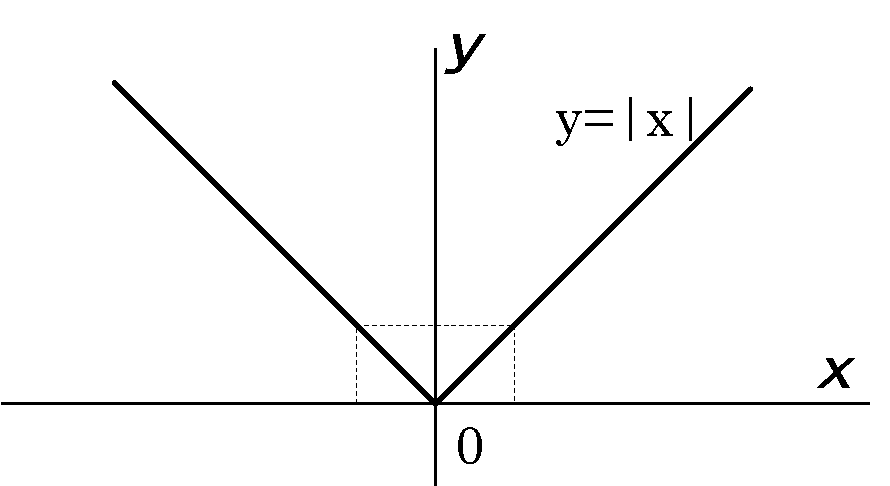 \(y=|x|\)のグラフ
\(y=|x|\)のグラフ