場所は瀬戸内海に面した小さな町で展開する話です。
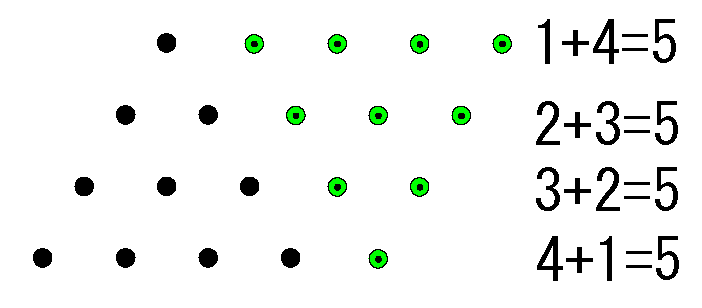
私が世話をする博士は母屋の離れの平屋に住み, 母屋には博士の義姉が住む, 私はその義姉から家政婦組合を通して雇われている。
義姉(未亡人)は博士の亡き兄の嫁であり, 義弟である博士の面倒を見ている。
面談において義姉からは「月曜から金曜日, 朝11時から夜7時までの勤務, 食事と買い物, 部家の清掃などをお願いします」
「また義弟が起こしたトラブルは離れの中で解決してください」
いろいろ聞きたいことがあるが, 彼女は余計な詮索を差しはさむ余地をあたえまい態度であった。
こうして私は博士の家政婦になった, 1992年の3月だった。
　博士は大学の数学教授だった17年前, 交通事故にあい, その後の記憶は80分しか持続できなくなってしまった。
したがい毎朝, 博士の家の玄関で, 私は自己紹介しなければならない。
「新しい家政婦です」と, そして博士は「君の靴のサイズは幾つかね」と聞く→「24です」と答える
「いさぎよい数字だ！…4の階乗だ」
「階乗とはなんですか」→「1から4までの自然数を全部掛け合わせると24になる」
「君の電話番号は何番かね」
「576の1455」です。→5761455
「素晴らしいね！　1億までに存在する素数の数に等しいね」

 このようにして毎日玄関で数字の会話が繰り返される。
博士の背広には沢山のメモ用紙がクリップされ, 袖口には私の似顔絵のメモが追加されている。
「君の誕生日いつかね」→「2月20日です」(220)
博士が外した腕時計の裏側には "学長賞 No.284" と刻印してあった。
220と284を博士は「どう思う」と聞くが「同じ3桁、どちらも偶数ぐらいしか…」
「この2つ数の約数で自分自身以外の約数を並べて加算してみよう」
・220:1 2 4 5 10 11 20 22 44 55 110→ 248
・248:1 2 4 71 142→ 220
「ごらんこんな素晴らしい一続きの数字の連なり、220の約数の合計が284。284の約数の合計が220」
「友愛数だ」「あのデカルトさえ一組しか見つからなかった組合わせだ」
「神の計らいを受けた絆で結ばれ合った数字なんだ」

　 博士の記憶が短時間をいいことにして、私は教えてもらったことを何度でも質問できた。
私は数学と聞くだけ寒気を感じたほど苦手だったが, 博士の教えてくれる数/数式には素直に受け入れられた。
それほど博士は上手な教え方で…数/数式に驚きのため息, 美を讃える言葉, 瞳の輝きは意味深いものだった。
あまりにも驚きの友愛数を知り, 他の友愛数を見つけようと考えるようになった。
「220と248以外の友愛数?」をたずねた。→「1184と1210だよ」
「4桁ですか,やっぱり私では到底無理ですね,息子にも手伝わせたんですが」
「君, 子供がいるのか」
「いくつだ, 今何してるのか, 一人か」博士は椅子から身を起こした。
シングルマザーでること, 10歳であり, 一人でほとんどできると答えた。
………博士は様々に子供を心配した。
「明日から子供は学校が終わったら直接ここにくるんだ, 宿題はここでやるんだ, 母親のそばにいられる。
明日になったらどうせ忘れるだろうと高をくくっているんじゃないか。 見くびってもらっちゃ困る。
約束を破ったら承知しないぞ」
博士のメモに "新しい家政婦さんの似顔絵" の横に "その息子10歳" が追加された。
それ以来, 息子は博士の家に通った。　それは博士が専門の医療施設に入るまで続いた。
息子は宿題をしたり、博士の数字/数学の話を聞いたりして楽しんだ。

 ランドセルを背負った息子が初めて 博士の家に来た時, 博士は両腕を広げ息子を抱擁し,
「よく来てくれたね ありがとう, ありがとう」と「息子の帽子をとり, 頭をなでて, 君はルート(\(\small{\sqrt{\ } }\) )だよ 」
息子の頭が平らで√記号に似ているからだ。
「どんな数字でも嫌がらず自分の中にかくまってやる, 実に寛大な記号…ルート(君)だ」
息子は博士独得の歓迎に慣れ, 帽子を脱ぎ, (√にふさわしい)頭のてっぺんを突き出した。
息子が来ると博士は必ず√記号の偉大さを讃えることを忘れなかった。
ルート が加わった3人の生活リズムは軌道にのりルートは博士に甘え, 思ったことも言えて, 博士もそれを受け入れ楽しんでいる。

私はようやく博士を外へ連れ出すのに成功した。
床屋に行き髪の毛をサッパリにして, その帰りベンチに座った。
そこで私は博士に「28の約数を足すと28なるんです」と言うと。
博士はベンチの下の小枝を拾い, 書き始めた。
「ほう……」
28=1+2+4+7+17
「完全数だ, 一番小さな完全数は6(=1+2+3)だ」
「次は496, 次に8128, さらに3350336,…」
「完全数以外は約数の和がそれ自身より大きい"過剰数" か, 小さい "不足数" か である」
「1だけ小さい不足数はあるが, 1だけ大きい過剰数は今だ発見されていない」
「せっかくなので完全数の性質を示そう→完全数は連続した自然数の和で表せる」

　博士とルートは野球ファン、しかも二人とも阪神ファン, 特に博士は江夏の熱狂ファンだった。
博士の中では江夏はまだ阪神の選手であった, そこで現役の江夏を知らないルートは図書館へ行き, 江夏の業績を調べた。
ある日, 二人の野球の会話で, 博士が「そうか, 阪神はそんなに調子がいいのか」「で江夏の防御率はいくつかね」… ルートは「江夏はトレードされ…それにもう引退したよ」と答えた。
博士は「えっ！」と絶句, 体が固まった。
いつも自分の記憶でカバーしきれない事柄も心静かに受け止めいたのに, 今回だけは勝手が違う。
その場をどう取りつくろっていいか見当がつなかい状態に陥っていた。
それを見て, ルートは自分が如何にひどいことを言ったのかを悟り、ショックを受けている。
博士は自分の仕事机に両肘をつき, 床屋できれいにした髪をかきむしった。
ルートはその博士の乱れた髪を撫でた。
……
この江夏問題は博士の短時間記憶のおかげで博士自身は忘れたが, 博士に二度と悲しませないと, 私たちは江夏に関してだけは嘘をつき通すことにした。
博士の書斎, 食堂で私とルートに聞かせてくれた数学の話に素数が一番多く登場した。
この世で博士が最も愛したのは素数だった。
はじめはなぜ, そんなに魅力があるのか不思議であったが, 博士が素数について語る態度のひたむきさに, 引きずり込まれてゆくうちに, 私たちに連帯感みたいものが生まれてきたみたいである。
私たちにとって夕方は貴重な時間だった, 朝は初対面同士として出会いお互いに緊張感が解かれ, そこにルートが帰ってくる, 無邪気な声が振りまかれる。
博士は同じ話を繰り返すが, 私たちは「その話は聞きました」と言わない固い約束をした。
こんな幼稚な私たちを数論学者のように扱ってくれる博士の努力に報いる必要があるが, 何よりも混乱せたくなかった。
　混乱は博士に悲しみを与える。(…江夏問題を思い出して…)
博士は失ったものの存在を知ることはなく, 何も失っていないのと同じである。…それを考えると私たちの約束はたやすいことであった。 　ルートの宿題が終わると, 「100までの素数を書いてみよう」と博士が書きはじめた。
「さあ, どう思う」, ルートは「みんなばらばらだ…それに"2"だけ偶数だよ」
「そうだ, 素数のなかで偶数は"2", 一個だけ, 素数番号①, 素数の先頭にたちリードオフマンで無限の素数を引っ張ている」
ルートは「淋しくないのかな」→「いやいや, さびしくなったら偶数の世界にいけばいいんだよ」
私も負けずに「17-19, 41-43など差が 2 である二つの素数の組がありますね」
「なかなかいい指摘だね、双子素数だよ」
「数が大きくなるにつれて素数の間隔が空いてくる, 双子素数も同様だ, 素数は無限にあるが, 双子素数が無限にあるかどうかまだ分からない」
博士の授業で不思議なのは彼は「わからない」という言葉を惜しみなく使うことだ。
分からないのは恥でなく、新たな真理への道標だった。
彼にとって, 手つかずの予想がそこにある事実を教えるのは, 既に証明された定理を教えるのと同じくらい重要だった。
「100を超え1万, 100万, 1000万…と大きくなると素数がでてこない…砂漠となる, それでもあきらめずに進むと素数 というオアシスがある, ともかくあきらめずに進むんだ！」
そのころ, 西日が部屋に差し込み, 夕食の時間がきた。

「ちょっとすまないが, 君…」いつもの頼む時のきまり文句。
びっしり数式が書かれた用紙の束を数学雑誌へ郵送するように頼まれた。
私は封筒に宛名"……懸賞問題応募係御中"を書き, 郵便局まで駆けていくのです。
この応募は博士の定期的のようだった。
懸賞といっても論文的なもの, あることの証明的なものです。
「証明に美しい, 美しくないがあるんですか」と聞くと→「もちろんだよ」

　4日間の連休明けの朝, 博士が見せるよそよしさが, いつにもなく かたくな であった。
私が買い物にでかけたて帰ると, ルートは包丁で手を切り, 博士はルートを抱えたまま嗚咽/うめきのような声をあげ, 台所の床にしゃがみこんで動揺しいていた。
博士は ルートを背負って診療所まで走った。
ルートが治療中、私と博士は薄暗い廊下に腰をかけた。
博士はレントゲン室の前に放射線の危険を示す三角形のマークを指さした。
「君は三角形を知っているかね」→「いいえ」私は "はい" と言える余裕はなかった。
博士は受付けにあった問診票の裏に書き始めた。