ここでは主に重積分(累次積分)とその変数変換、ベクトルの外積などを用いて説明していきます。
復習として、必要な個所に、【参照先】のリンクをおいています、クリックしてみてください。
|
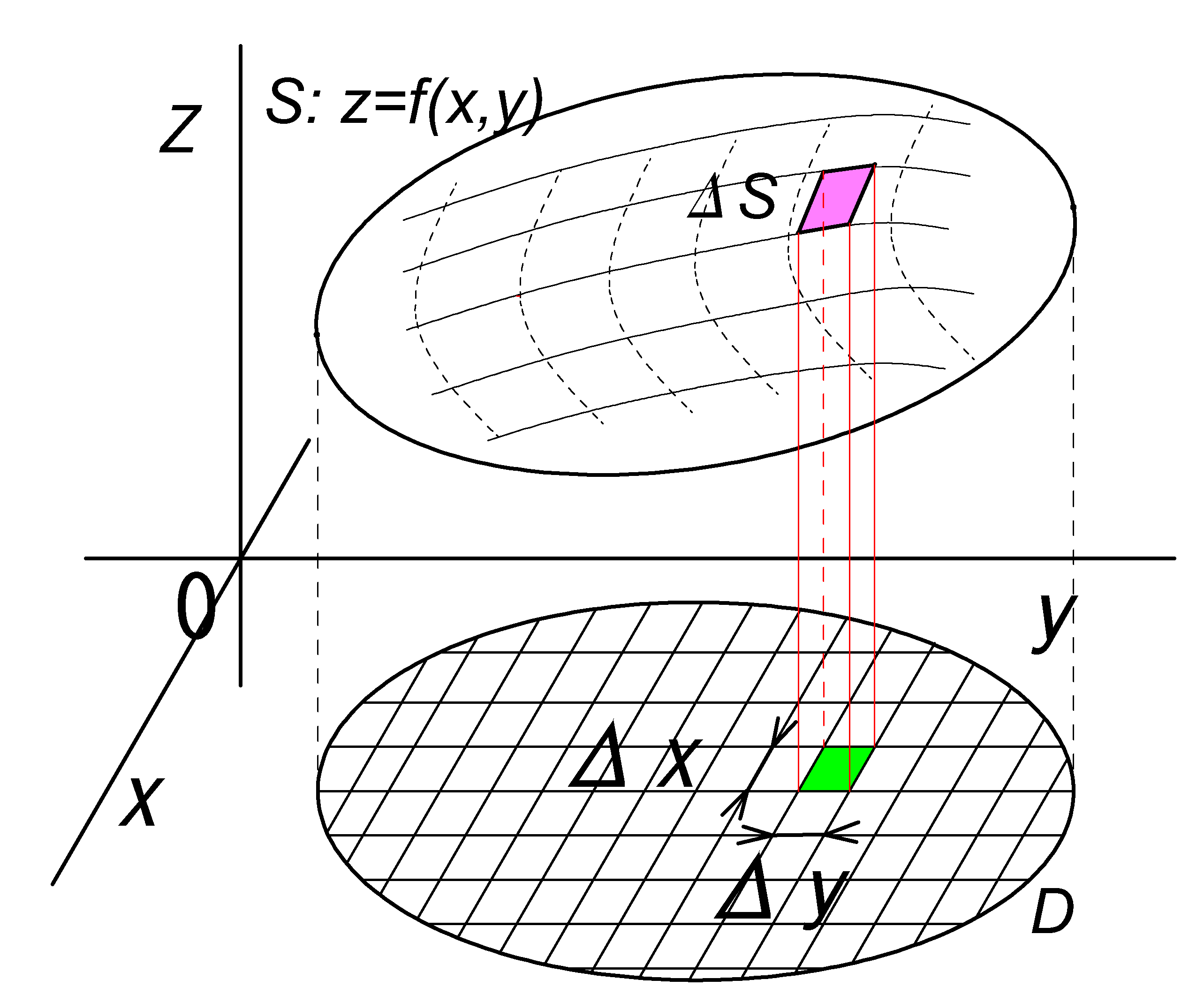
スカラー場の面積分1
fig1 において、スカラー場\(\phi(x,y,z)\)と曲面S は\(f(x,y,z)\)とする。
このときスカラー場\(\phi(x,y,z)\) の曲面S における面積分は次式により定義される。
\( \dsii_S \phi(x,y,z) dS\)
\(=\dsii_D \phi(x,y,z) \sqrt{(\pder{f}{x})^2+ (\pder{f}{y})^2 + 1\ }\ dxdy\) \(\ :❷\) |
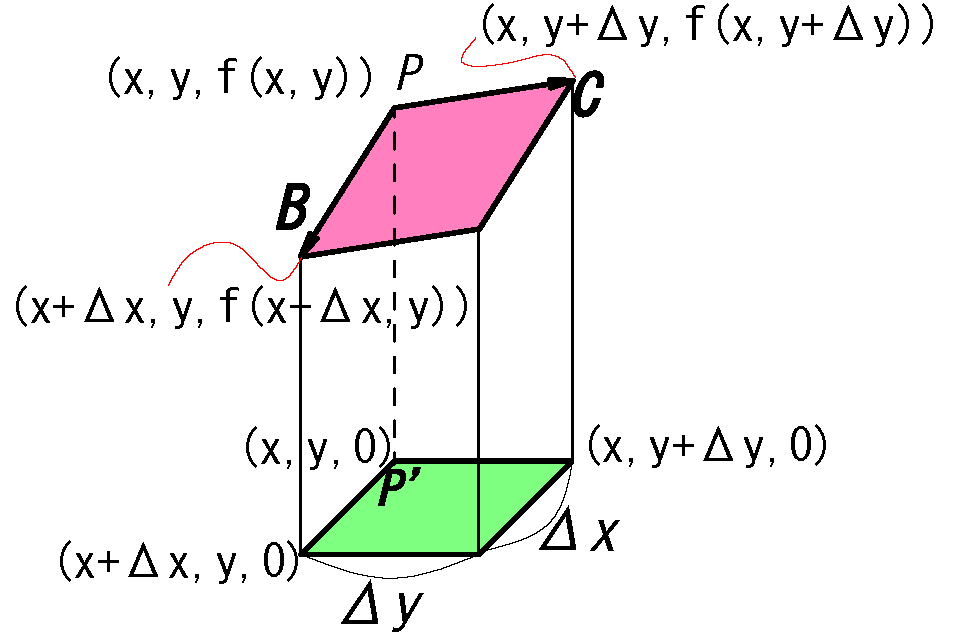
図からベクトルの成分を求める(=終点-始点)
例:\(\bv{B}\)\(=(x_{+\Delta}-x,\ y-y,\ f(x_{+\Delta},y)-f(x,y))\)
\(\bv{B}=( Δ x,\ 0,\ f(x_{+Δ},\ y)-f(x,y))\)
\(\bv{C}=( 0,\ Δ y,\ f(x,\ y_{+Δ})-f(x,y))\)
ベクトル積を外積、クロス積などいう。
ベクトルの大きさは絶対値で表し、3平方の定理により計算(各成分の2乗の和の平方根)
例:ベクトル\(A=(a,b,c)\) \(|A|=\sqrt{a^2+b^2+c^2}\)
\(\bv{B} \x \bv{C}\)
\(=\left(
\begin{array}{c}
Δ x \\
0 \\
f(x_{+Δ},\ y)-f(x,y)
\end{array}
\right)
\)
\( \x \)
\( \left(
\begin{array}{c}
0 \\
Δ y \\
f(x, y_{+Δ})-f(x,y)
\end{array}
\right)
\)
☞
上記のベクトル積の計算の
【参照先】
\(=
\left(
\begin{array}{c}
-(f(x_{+Δ}, y)-f(x,y))Δy\\
-(f(x, y_{+Δ})-f(x,y))Δx \\
ΔxΔy
\end{array}
\right)
\)
\(G=\frac{(f(x_{+Δ}, y)-f(x,y))}{Δx}\)
\(H=\frac{(f(x, y_{+Δ})-f(x,y))}{Δy}\)
\(ΔS\)\(=|\bv{B} \x \bv{C}|\) \(=\sqrt{G^2+H^2+1}\)\(ΔxΔy\) \(:(a)\)
\(\Delta x\) と \(\Delta y\) を 0 に近付けると:
\(\pder{f}{x}=\displaystyle \lim_{\Delta x \to 0} \frac{(f(x_{+Δ}, y)-f(x,y))}{Δx}\)
\(\pder{f}{y}=\displaystyle \lim_{\Delta y \to 0} \frac{(f(y_{+Δ}, y)-f(x,y))}{Δy}\)
従って式❷が導かれる:
\( \dsii_S \phi(x,y,z) \underline{dS}\)
\(=\dsii_D \phi(x,y,z) \underline{ \sqrt{(\pder{f}{x})^2+ (\pder{f}{y})^2 + 1\ }\ dxdy }\) \(\ :❷\)
\(\bv{B}=( Δ x,0,f({x+Δx},\ y)-f(x,y))\) (※)
\(\bv{C}=( 0,Δ y,f(x,y+Δy)-f(x,y))\)
\(\displaystyle \pder{\bv{B}}{x}\)\(=(1,0,\pder{f}{x})\) (※)
\(\displaystyle \pder{\bv{C}}{y}\)\(=(0,1,\pder{f}{y})\)
(※):ベクトルB の成分ごとに微分すると:
\(\pder{(\Delta x)}{x}\) \(=\displaystyle \lim_{\Delta x \to 0} \frac{\Delta x }{\Delta x }=1\)
\(\pder{(0)}{x}\) \(=0\)
\(\displaystyle \lim_{\Delta x \to 0} \frac{f(x+Δx),y)-f(x,y)) }{\Delta x } \)\(=\dspder{f}{x}\)
\(y\)についての偏微分も同様。
|
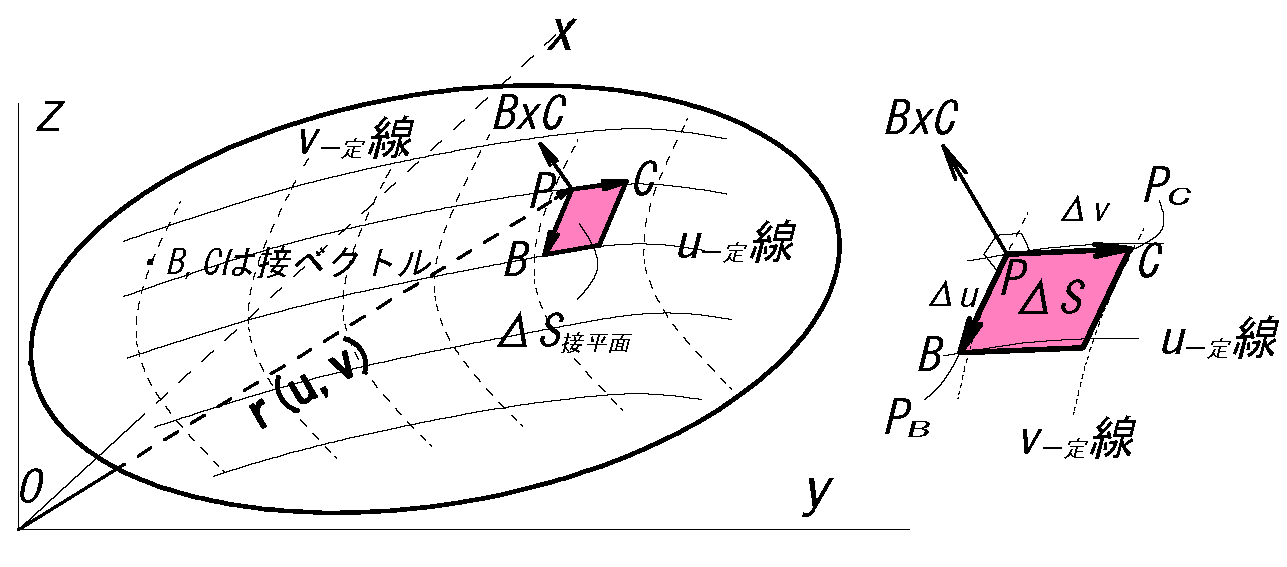
スカラー場の面積分2
fig3 においてスカラー場\(\phi(x,y,z)\)と を パラメータ\(u,v\)を使い表わす。
また、曲面S は\(\bv{r}(u,v)\) で表されている。 スカラー場: \(\phi(x,y,z)=\phi(u,v)=\phi(x(u,v),y(u,v),z(u,v))\) 曲面S: \(\bv{r}(u,v)=\bv{r}(x(u,v),y(u,v),z(u,v))\) このときスカラー場\(\phi(u,v)\) の曲面S における面積分は次式により定義される。
\( \dsii_S \phi(x,y,z) dS\)
\(=\dsii_D \phi(x(u,v),y(u,v),z(u,v))\) \( |\pder{\bv{r}}{u} \x \pder{\bv{r}}{v}| \ dudv\) \(\ :❹\) |
\(\bv{B}=\dspder{\bv{r}}{u}\Delta u\) \(,\quad \) \(\bv{C}=\dspder{\bv{r}}{v}\Delta v\)
\(\Delta S=|\bv{B} \x \bv{C}|\)\(=|\dspder{\bv{r}}{u}\Delta u \x \dspder{\bv{r}}{v}\Delta v|\)
\(=|\dspder{\bv{r}}{u} \x \dspder{\bv{r}}{v}|\Delta u \Delta v\)
\( \dsii_S \phi(x,y,z) \underline{dS}\) \(=\dsii_D \phi(x(u,v),y(u,v),z(u,v)) \) \( \underline{|\pder{\bv{r}}{u} \x \pder{\bv{r}}{v}| \ dudv } \) \(\ :❹\)
(注):上記の微小の接平面の\(dS(\Delta S)\)を「面積要素」、「面積素」、「面素」などという。
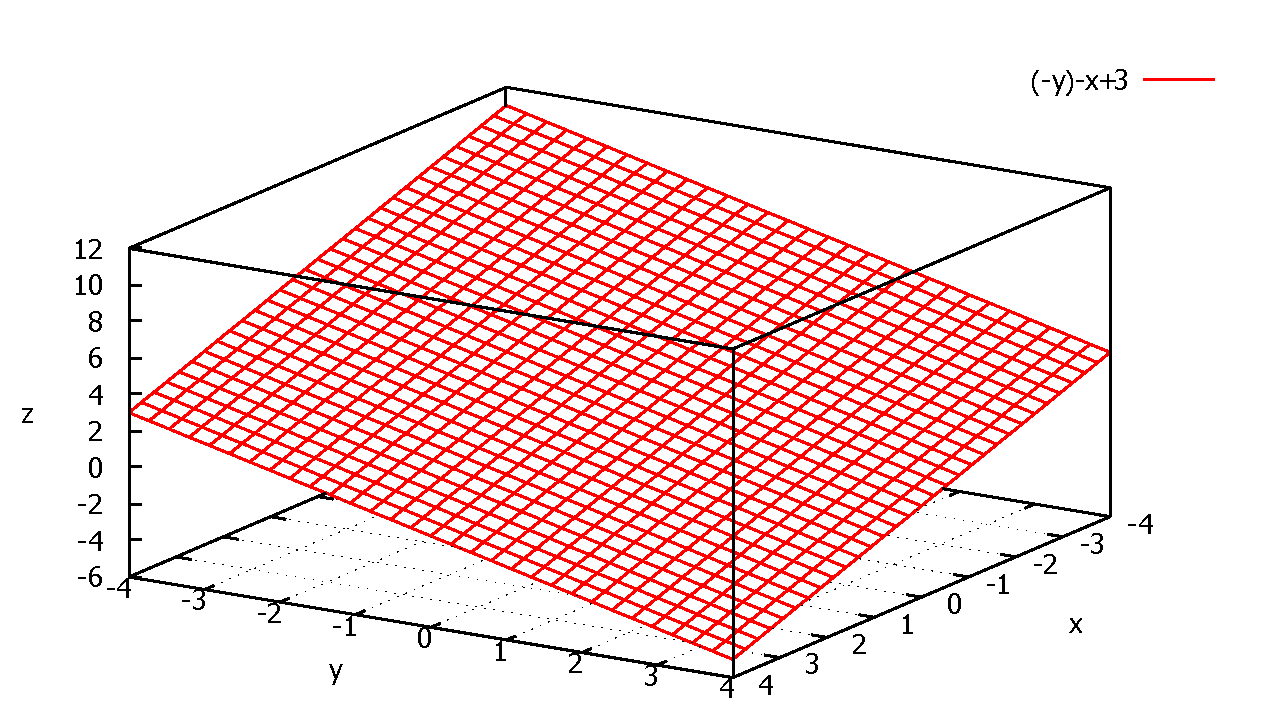
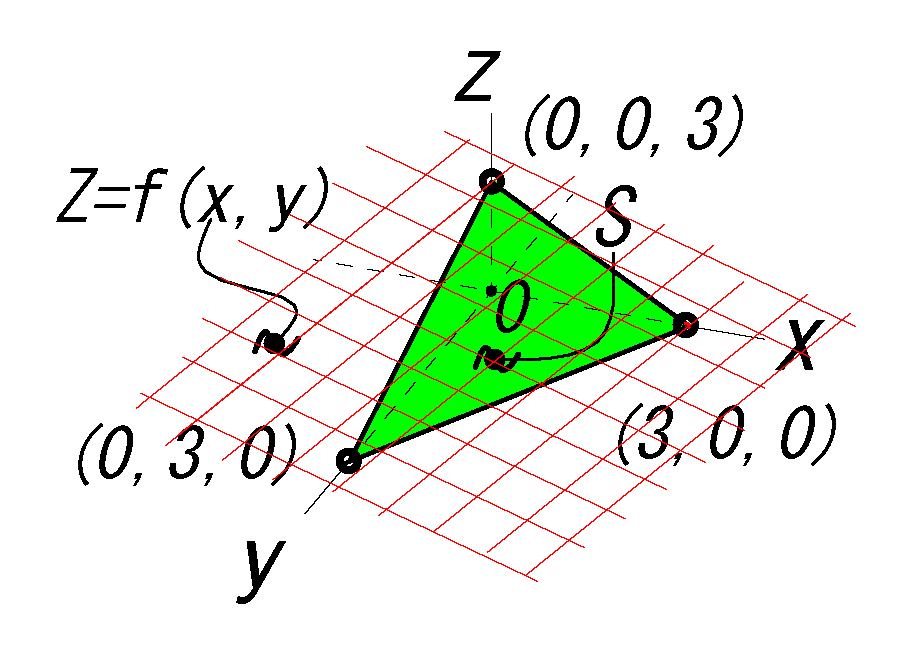
\(D= \{ (x,y)| 0≤ x ≤3 ,\quad 0 ≤ y ≤ 3-x \} \)
\( z=f(x,y)=3-x-y\) だから:
\( \pder{f}{x}=-1\) \(, \) \( \pder{f}{y}=-1\)
\( \dsii_S \phi(x,y,z) dS\)
\(=\dsii_D (x+2y) \sqrt{(-1)^2+ (-1)^2 + 1\ }\ dxdy\)
\(=\dsii_D (x+2y) \sqrt{3}\ dxdy\)
\(=\sqrt{3} \dsi_0^3 \color{red}{ \dsi_0^{3-x} (x+2y) dy } \ \ dx \) :(※a)
\(=\sqrt{3} \dsi_0^3 \color{red}{ \left[ xy+y^2 \right]_0^{3-x} } \ \ dx \)
(※a)
\([xy+y^2]_0^{3-x}=x(3-x)+(3-x)^2\) \(=3x-x^2+9-6x+x^2\)\(=-3x+9\)
\( z=f(x,y)=3-x-y\)
\( \phi=x+2y \)
\(D= \{ (x,y)| 0≤ x ≤3 ,\quad 0 ≤ y ≤ 3-x \} \)
\( r(u,v)\)
\(=\left(
\begin{array}{c}
u\\
v\\
3-u-v
\end{array}
\right)
\)
\(,\)
\( \dspder {r(u,v)}{u}\)
\(=\left(
\begin{array}{c}
1\\
0\\
-1
\end{array}
\right)
\)
\(,\)
\( \dspder {r(u,v)}{v}\)
\(=\left(
\begin{array}{c}
0\\
1\\
-1
\end{array}
\right)
\)
偏微分どうしの外積とその大きさ(絶対値):
\( \dsii_S \phi(x,y,z) dS\)
\(=\dsii_D (u+2v)\) \( |\pder{\bv{r}}{u} \x \pder{\bv{r}}{v}| \ dudv\)
\(=\dsii_D (u+2v)\) \( \sqrt{3} \ dudv \)
\(=\sqrt{3} \underline{ \dsi_0^3 \dsi_0^{3-u} (u+2v) dv \ du } \)
\(=\sqrt{3} \dsi_0^3 \left[ uv+v^2 \right]_0^{3-u} \ du \)
\(=\sqrt{3} \dsi_0^3(-3u+9)du \)
\(=\sqrt{3} \left[ \frac{-3}{2}u^2+9u \right]_0^3\)
\( \iint_S \phi(x,y,z) dS\) \(=\iint_D \phi(x,y,z) \sqrt{(\pder{f}{x})^2+ (\pder{f}{y})^2 + 1\ }\ dxdy\) \(\ :❷\)
\(\iint_D \underline{ f(x,y) } dxdy\) \(=\iint_D \underline{\sqrt{a^2-x^2-y^2} } dxdy\)
但し\(\underline{z=f(x,y)≥0}\):半球
(全球体のとき \(z=\pm f(x,y)\) である)
\(D=\{(x,y)| x^2+y^2 ≤a^2\)\(,\ -a≤x≤ a,\ -a≤y≤a \} \)
また \(x=r conθ,\ y=r sinθ\)であるから
\(D'=\{(r,θ)|(rcosθ)^2+(rsinθ)^2≤a^2\)\(,\ 0≤r≤a ,\ 0≤θ≤2\pi\} \)
この場合のヤコビアン \(\underline{J=r}\) である。
\(\dsii_D f(x,y) dxdy\) \(=\iint_D \sqrt{a^2-x^2-y^2} dxdy\)
\(=\iint_D' \sqrt{q^2-(rcosθ)^2-(rsinθ)^2} |J|dr dθ \)
\(=\int_0^{2\pi} \left( \int_0^a \sqrt{a^2-(rcosθ)^2-(rsinθ)^2} \right. \)
\(\left. rdr \right) dθ \)
\(=\int_0^{2\pi} \left(\underline{ \int_0^a \sqrt{a^2-r^2}\ rdr} \right) dθ \)
\(u=a^2-x^2-y^2\) とおき \(z=\sqrt{u}=u^{\frac{1}{2}}\)
\(\pder{f}{x}=\frac{1}{2} u^{-\frac{1}{2}}(-2x)=\frac{-x}{\sqrt{u}}\)
\(\pder{f}{y}=\frac{1}{2} u^{-\frac{1}{2}}(-2y)=\frac{-y}{\sqrt{u}}\)
\( =\iint_D (q+kz) ( \sqrt{ (\frac{x^2+y^2+a^2-x^2-y^2} {u} } )\ dxdy \) \( =\iint_D (q+kz) ( \sqrt{ (\frac{a^2} {z^2} } )\ dxdy \)
\(=\iint_D (q+kz)\frac{a}{z} dxdy\) \(=\iint_D ( q\frac{a}{z}+ak) dxdy\) \(=\iint_D ( q\frac{a}{\sqrt{ a^2 \color{fuchsia}{-x^2-y^2} }}+ak) dxdy\)
\(\underline{t^2=a^2-r^2 }\) \(,\) \(\frac{d}{dr}(t^2)=(a^2-r^2)'\)
\(2t \frac{dt}{dr}=-2r\) \(\ \) \(\therefore rdr=-tdt\)
\(\underline{r:0 →a}\) に対し \(\underline{t:a →0 }\)
\(\int_0^a ( \frac{r}{\sqrt{1^2-r^2}} )dr\)
\(=\int_a^0 \frac{-1}{t} tdt\)
\(=\int_a^0 -1 dt\) \(=[-t]_a^0\)\(=a\)
あとは与題の\(\phi_1,\phi_2,\phi_3\)を代入するだけ。
これより以下が求まる:
