湘南理工学舎・微分積分・重積分、曲面積

対象の曲面 \(z=f(x,y)\) は\(xy\)平面にある有界閉集合\(D\) で定義され、\(C^1\)級である。
（曲面の接線を計算するので偏微分を使う！）
fig2 の微小曲面の接平面（四辺形）を構成するベクトル\(u,v\)は：
（以下はベクトル成分表示、上から \(x,y,z\)成分である）
\(u= \begin{pmatrix} \Delta x \\ 0\\ \Delta h_x \end{pmatrix} \) \(\quad v= \begin{pmatrix} 0 \\ \Delta y\\ \Delta h_y \end{pmatrix} \)

\(\Delta h_x = \dd{z}{x}\Delta x　\quad \) \(\Delta h_y = \dd{z}{y}\Delta y　\)

（参）ベクトルの外積の計算例：

\(a= \begin{pmatrix} a_1 \\ a_2 \\ a_3 \end{pmatrix} \) \(,\) \(b= \begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix} \) のベクトル積は：

\(　a \x b　\) \(= \begin{pmatrix} a_2 b_3 - a_3 b_2 \\ a_3 b_1 - a_1 b_3 \\ a_1 b_2 - a_2 b_1 \end{pmatrix} \)

上記の計算例を参考にして、\(u,v\) のベクトル積は：
\(u \times v=\) \( \begin{pmatrix} - \Delta h_x \Delta y \\ - \Delta h_y \Delta x \\ \Delta x \Delta y \end{pmatrix} \)

これはベクトルの成分表示である。
ベクトル積の大きさである面積は以下となる。
\( \Delta S= \sqrt{ (\Delta h_x \Delta y)^2+(\Delta h_y \Delta x)^2 + (\Delta x \Delta y)^2 } \)

\(= \sqrt{ (\dd{z}{x}\Delta x \Delta y)^2+(\dd{z}{y}\Delta y \Delta x)^2 + (\Delta x \Delta y)^2 } \)

\(= \sqrt{ (\dd{z}{x})^2 +(\dd{z}{y})^2 + 1 } \ \Delta x \Delta y \)

分割をさらに小さくして\(|\Delta| → 0\)にして足し合わすと、❶の公式を得る。
\( S= lim_{|\Delta| \to 0} \displaystyle \sum \Delta S\)

\(\color{blue}{ = \iint_D \sqrt{ (\dd{z}{x})^2 +(\dd{z}{y})^2 + 1 } \ dx\ dy}\)\(:❶ \)

\(\color{blue}{ = \iint_D \sqrt{ (f_{x})^2 + (f_{y})^2 + 1 } \ dx\ dy }\)\(:❶’ \)

球の方程式は \(k^2=x^2+y^2+z^2\) である。

\(f(x,y)=\)\(z=\sqrt{k^2-x^2-y^2}\)

積分領域は\(x,y\)平面での半径\(k\) の円です。
\(D=\{(x,y)|x^2+y^2≤k^2\}\)

地球の赤道を\(x,y\)平面において北半球の表面積を求めるイメージ。

\( u=k^2-x^2-y^2 \)とおいて
\( f_x=-2x \frac{1}{2} u^{-\frac{1}{2}}\)\(=-x \frac{1}{\sqrt{k^2-x^2-y^2}}　\)

\( f_y=-2y \frac{1}{2} u^{-\frac{1}{2}}\)\(=-y \frac{1}{\sqrt{k^2-x^2-y^2}}　\)

\(S=2 \iint_D \sqrt{ (f_{x})^2 + (f_{y})^2 + 1 }\ dx dy\)

\(=2 \iint_D \sqrt{ \left[(-x)^2+ (-y)^2 \right] \left[u^{-\frac{1}{2}} \right]^2 +1 }\ dx dy\)

\(=2 \iint_D \sqrt{ \frac{x^2+y^2 + (k^2-x^2-y^2)}{(k^2-x^2-y^2)} }\ dx dy \)

\(=2 k \iint_D \sqrt{ \frac{1}{(k^2-x^2-y^2)} } dx dy\)

ここから先は極座標変換を利用して計算する。【参照先】
（積分計算が簡単になる）

\(x=kcos\ θ\) \(,\ y=ksin\ θ\)　
直交座標から極座標への変数変換は、 \(dx\ dy=r dr\ dθ \)
の関係による面積要素の変換が行われている。
\(\iint_D f(x,y) dxdy\) \(=\iint_{D'} f(r\ cosθ,r\ sinθ) r\ \ dr\ dθ\)　

\(=2 k \iint_{D'} \sqrt{ \frac{1}{(k^2-r^2)}} r \ dr\ dθ \)

\(=2 k \int_0^{2\pi} \left( \int_0^k \frac{r}{\sqrt{(k^2-r^2)}} dr \right) \ dθ \)

\((k^2-r^2)=u\)とおいて置換積分する
\(\int_0^k \frac{r}{\sqrt{(k^2-r^2)}} dr\) \(=\int_0^k \frac{r}{\sqrt{u}} dr\) \(=\int_0^k -\frac{1}{2r} r (u)^{\frac{-1}{2}}du\)

\(=-\frac{1}{2}\int_0^k (u)^{\frac{-1}{2}}du\) \(=-[u^{\frac{1}{2}}]_0^k\) \(=-[\sqrt{k^2-r^2}]_0^k=k\)

\(=2 k \int_0^{2\pi} k \ dθ \)

\(=2 k [k θ ]_0^{2\pi}\) \(=2 k k 2\pi = 4\pi k^2\)

関数\(f(x)\)が積分領域の閉区間[a,b]において可積分。
\(f(x)\)と\(x=a,\ x=b\) と x軸で囲まれたグラフ（面積である）を\(x\) 軸を中心に回転させてできる体積を求める。
この立体の\(x\)軸上の断面は半径が\(f(x)\)の円である…これがポイント。
・中心について対称な図形。
・半径\(f(x)\)が負なるが、次式で2乗となるのでそのままでよい。
これより断面積は：
\( S=\pi f(x)^2\)

従い、回転体の体積\(V\)は1変数の積分により求まる。
\(V=\int_a^b \pi f(x)^2 dx\)

\(\color{blue}{=\pi \int_a^b f(x)^2 dx }\quad ：❷ \)

\(xy\)平面上のx について\(C^1\) 級である関数f(x)をx軸の中心に回転してできる立体の曲面積（表面積）を求める。
•回転の中心は z=0 でx軸が回転の中心。
•x軸の積分領域は閉区間[a,b]

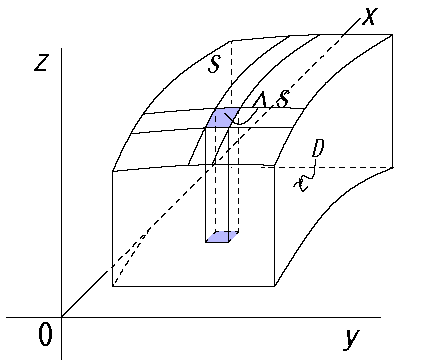
回転によりできる曲面だが、公式❶を使い解くので上項のような回転運動により求めるイメージではない。
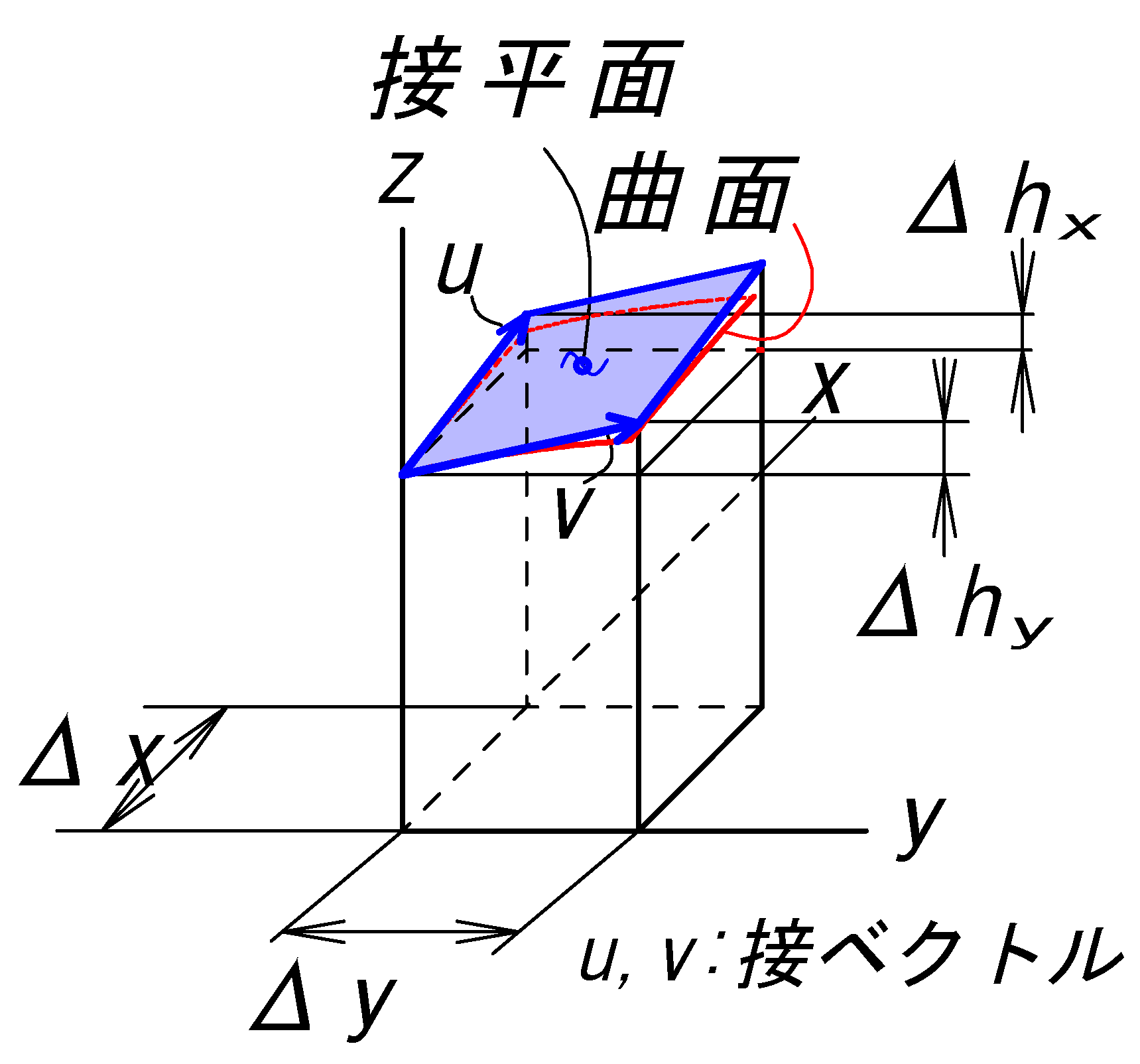
（曲面の微小部分を接平面で近似させる方法の１項により求める）
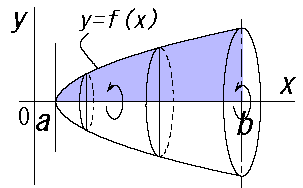
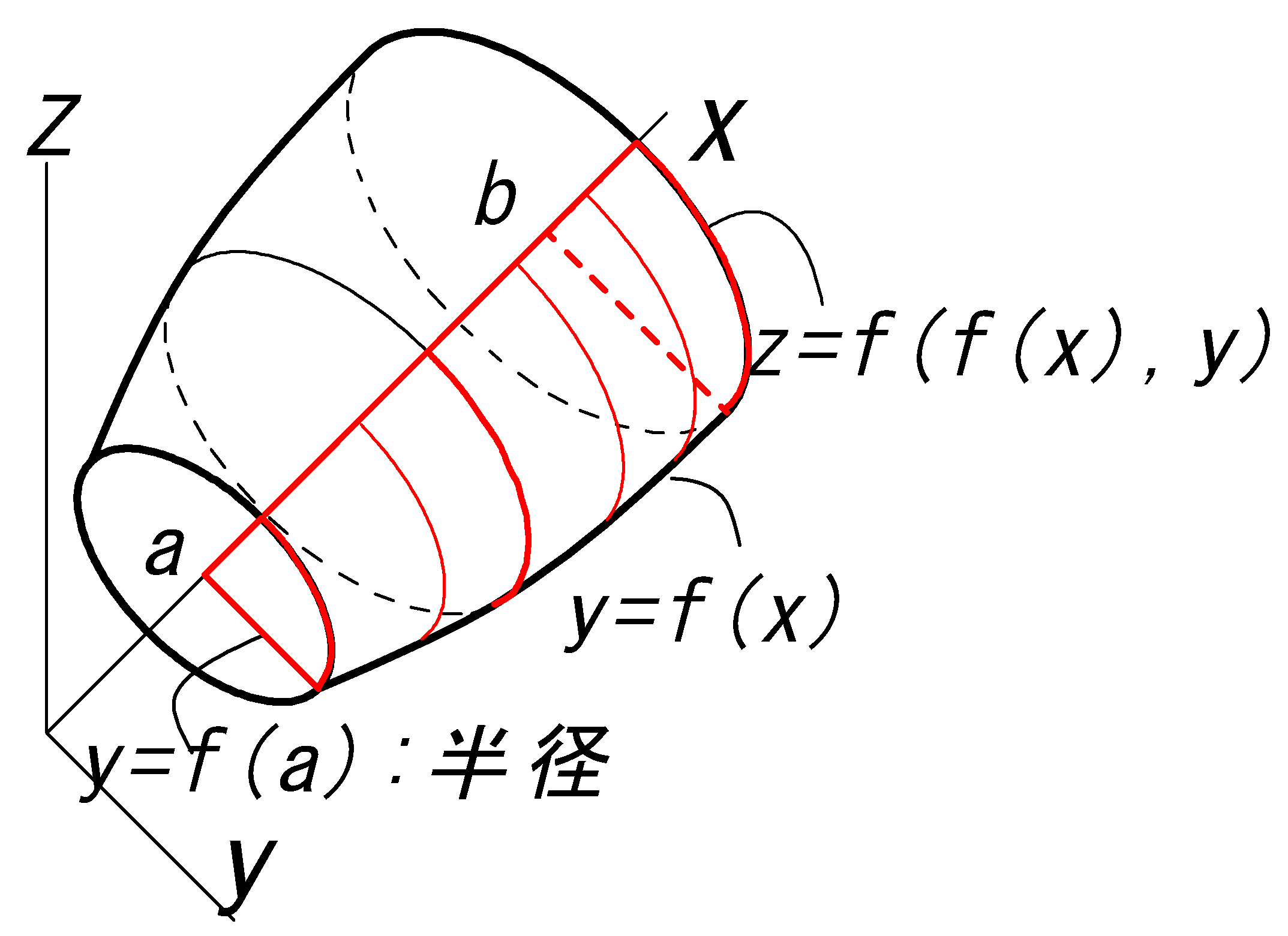
半径\(f(x)\)が作る円の曲面全体の1/4 \((y≥0,z≥0)\)を、閉区間\(x=[a,b]\)について積分、これを４倍する。
具体的に、求める解は閉区間[a,b]における円の曲面\(z=\sqrt{f(x)^2-y^2}\)の面積を求めることである。
\(z=f(x,y)=\sqrt{ f(x)^2-y^2} \)　

次に偏微分\(f_x ,\ f_y\) を求める。

\(f(x)^2-y^2=u\) とおく。
\(\frac{\partial}{\partial x}\sqrt{ f(x)^2-y^2}\)\(=\dd{\sqrt{u}}{x}\)

\(=\frac{d(\sqrt{u})}{du}\frac{d(f(x)^2-y^2) }{dx}\) \(=\frac{1}{2} u^{-\frac{1}{2}} 2f(x) f'(x) \)

\(\therefore　f_x= \frac{1}{\sqrt{ f(x)^2-y^2}} f(x) f'(x) \)

（\(f(x)=z\)とおく）
（\(\frac{d(z^2)}{dx}=\frac{z^2}{dz}\frac{z}{dx}=2f(x) f'(x)\)）

\(\frac{\partial}{\partial y}\sqrt{ f(x)^2-y^2}\)\(=\dd{\sqrt{u}}{y}\)

\(=\frac{d(\sqrt{u})}{du}\frac{d(f(x)^2-y^2) }{dy}\) \(=\frac{1}{2} u^{-\frac{1}{2}} -2y \)

\(\therefore　f_y= -\frac{1}{\sqrt{ f(x)^2-y^2}} y \)

重積分の積分領域D：
\(D=\{(x,y):a≤x≤b,\ 0≤y≤f(x),\ y(x)≥0\}\)

\(S= 4\iint_D \sqrt{ (f_{x})^2 + (f_{y})^2 + 1 } \quad dx\ dy \)

\(= 4\iint_D \sqrt{ \frac{f(x)^2 f'(x)^2+y^2+f(x)^2-y^2 }{f(x)^2-y^2} } \quad dx\ dy \)

\(= 4\iint_D \sqrt{ \frac{f(x)^2 f'(x)^2+f(x)^2}{f(x)^2-y^2} } \quad dx\ dy \)

\(= 4\int_a^b \left(\int_0^{f(x)} \underline{f(x) \sqrt{ f'(x)^2+1}} \sqrt {\frac{1}{f(x)^2-y^2}} \ dy \right) dx \)
下線部は\(y\) については定数扱い

\(= 4\int_a^b \underline{f(x) \sqrt{ f'(x)^2+1}} \left[ sin^{-1}\frac{y}{f(x)} \right]_0^{f(x)} dx \)

\(= 4\int_a^b f(x) \sqrt{ f'(x)^2+1} (sin^{-1} 1) dx \)

\(= 2 \pi \int_a^b f(x) \sqrt{ f'(x)^2+1} dx \)

一般式としてはf(x)は絶対値にして：
\(S\color{blue}{= 2 \pi \int_a^b |f(x)|\sqrt{ f'(x)^2+1} dx}\quad ❸ \)

公式❸より求める式は：
\(S= 2 \pi \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}|cos\ x|\sqrt{ sin^2x+1} dx\)

被積分関数はここから引用する【参照先】
(この積分を解くのは、ちょっとハードなので前のテーマの解を利用させてもらう。）
\(I=\int cos\ x　\sqrt{ sin^2x+1} dx\)

\((-\frac{\pi}{2}≤x≤\frac{\pi}{2})\)なので\(f(x)\)は非負、絶対値は外せる。

\(=\frac{1}{2} \left[ \sqrt{1+sin^2x}\ sin\ x \right.　\) \( \left. +log|\sqrt{1+sin^2x} +sin\ x| \right] \)
\(S= 2 \pi \left[\ I\ \right]_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \) (：1周期の半分の波形)
\(=2 \pi \frac{1}{2}\left[(\sqrt{2}+log|\sqrt{2}+1|) \right. \) \(\left. -(\sqrt{2}+log|\sqrt{2}+1|)\right] \)

\(=\pi (2\sqrt{2} + log | \frac{\sqrt{2}+1}{\sqrt{2}-1}|)\) \(=\pi (2\sqrt{2} + log | \frac{(\sqrt{2}+1)^2}{1}|\)

\(=\pi (2\sqrt{2} + 2log | \sqrt{2}+1|)\)

\(=2\pi (\sqrt{2} + log | \sqrt{2}+1|)\)

重積分5/ 曲面積・その他

[コーヒーブレイク/閑話］…お疲れ様でした。