重積分(2) 累次積分

 前回は重積分の面積確定による積分可能性について学びました。
今回は重積分の具体的な計算法の累次積分(逐次積分ともいう）について学びます。
1変数の定積分のときはその不定積分が求まれば、定積分（リーマン積分）を解くことができました。
2変数以上の多重積分では２変数のうち１変数を固定して（定数扱い）、1変数関数の定積分に帰着させ、定積分を繰り返す方法が累次積分です。
（重積分の英名「repeated integral」の読んで字の如しです）

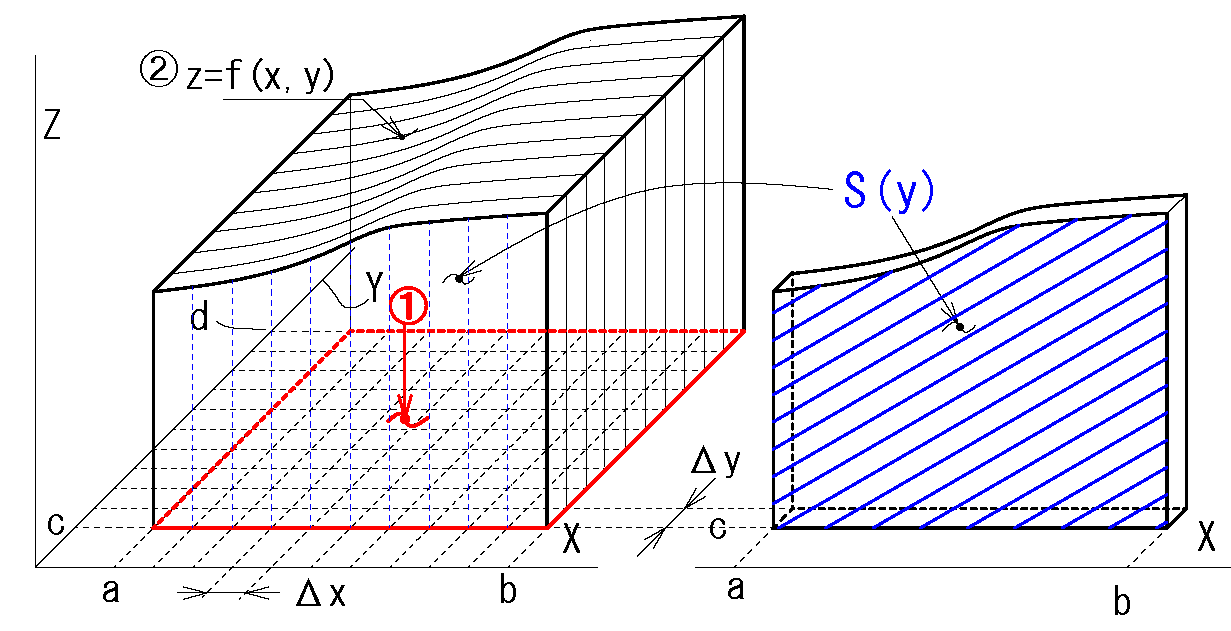
 はじめは簡単にするため、定義域の積分領域は長方形の有界閉区間\(D=[a,b]\times[c,d]\)とする。
関数\(f(x,y)\) は \(D\)上で定義された 有界で積分可能 な関数。
（下線部は「連続」でもよい　∵連続なら積分可能であるから）
図の場合はx-z平面のy に垂直な面で薄く切ってできた断面のイメージです。

リーマン積分と同様に 領域\(D\) を以下のように\(\Delta\)分割（細かく分割）します。
\(\Delta(x):\) \( (a=)x_0<x_1<x_2<…x_{n-1}<x_n(=b)\)
\(\Delta(y):\) \( (c=)y_0<y_1<y_2<…y_{n-1}<y_n(=d)\)

小分割 \(D_{ij}＝[x_{i-1},x_{i}] \x [y_{j-1},y_{j}]\) の中の任意点を\( \color{red}{(x'_{ij},y'_{ij})} \)とする。
その任意点に対応する関数を\(f\color{red}{ (x'_{ij},y'_{ij}) }\)とする。
これのリーマン和は次のようになる。
\(V_n=\displaystyle \sum_{j=1}^m \left(\ \underline{ \displaystyle \sum_{i=1}^n f \color{red}{(x'_{ij},y'_{ij}) } (x_i-x_{i-1})}\ \right )\)\((y_j-y_{j-1})\)

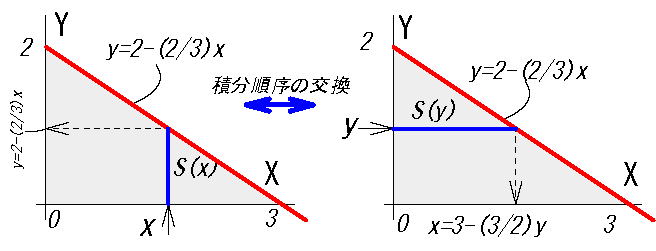
\([a,b]の\Delta\)分割を小さくすれば下線部は
（ｙを固定しxについて積分する形）
\( \int_a^b f(x,y) dx\) \(⇒S(y)\)

\(V_n=\displaystyle \sum_{j=1}^m \left( \int_a^b f(x,y)dx \right) \) \((y_j-y_{j-1})\)

さらに\([c,d]の\Delta\)分割を小さくすると
\(V=\int_c^d \left( \int_a^b f(x,y)dx \right) dy\)\(=\iint_D f(x,y) dxdy\)

これが累次積分の式です。（（）内を先に積分する）
次のような表記もあります。（変数が増えると分かり易い）
\(V=\int_a^b dx \int_c^d f(x,y) dy\)

ここまで累次積分の概念について説明しました。
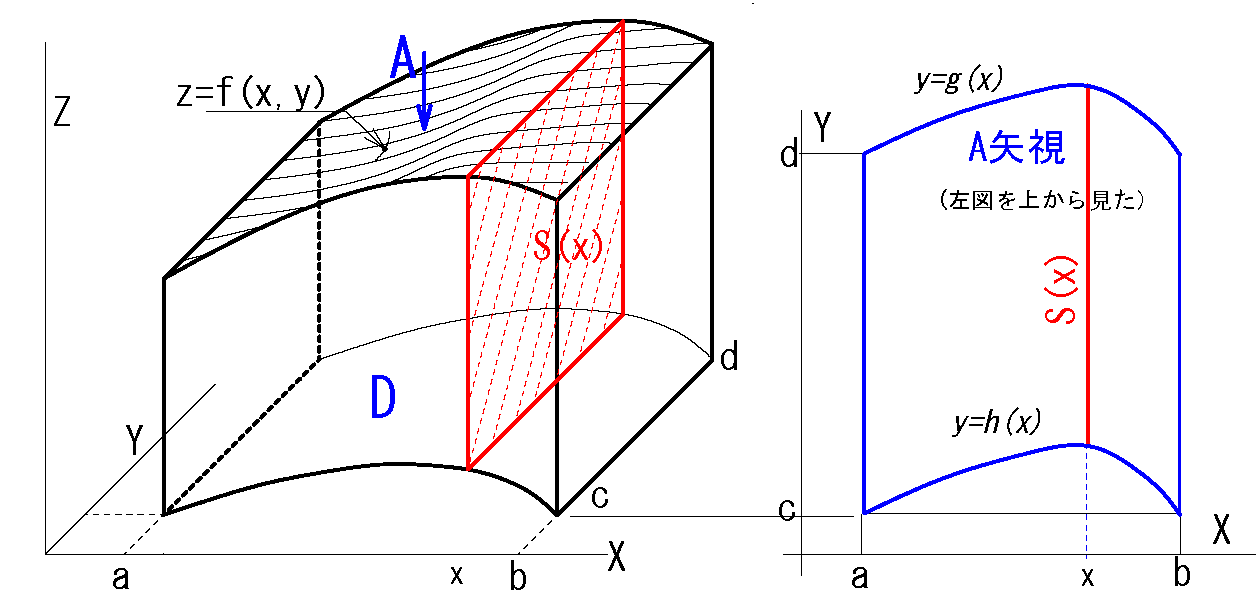
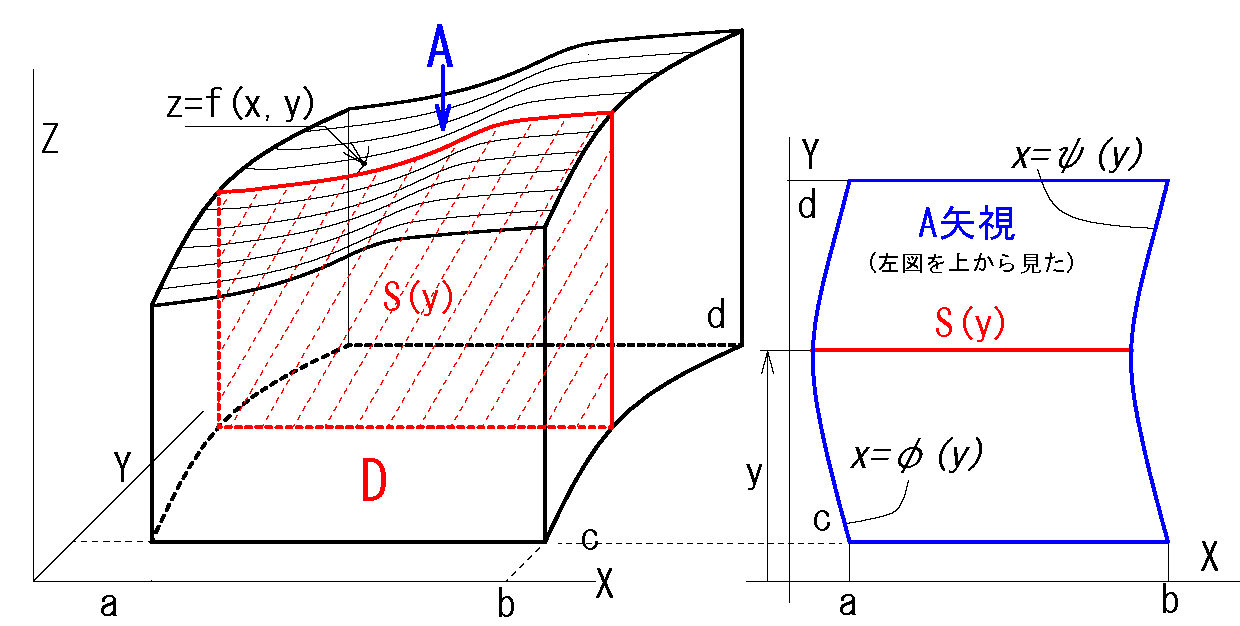
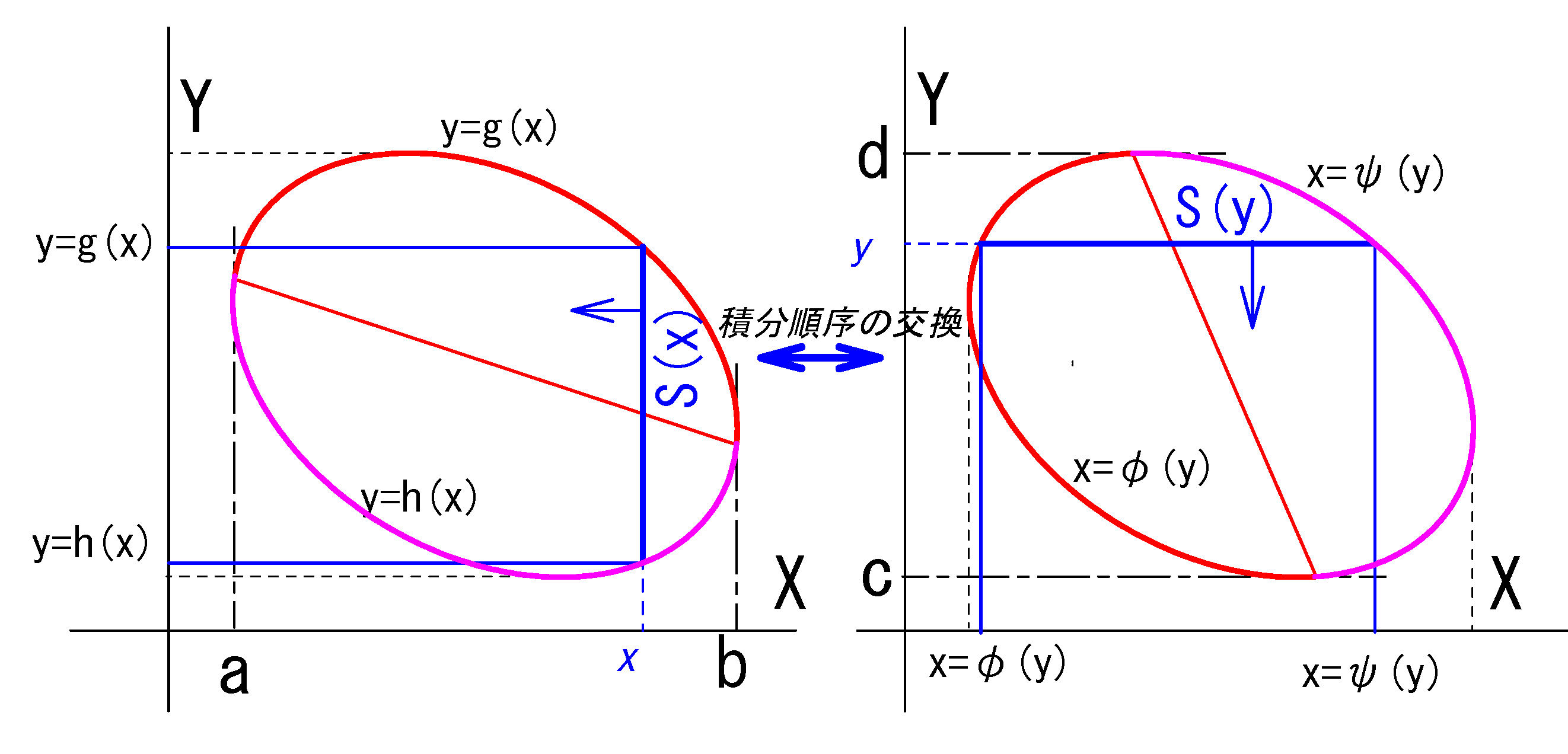
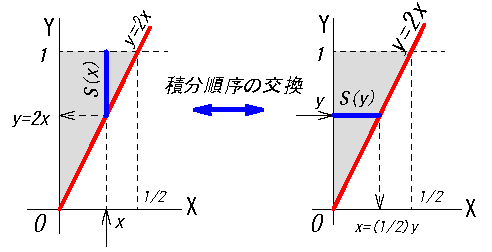
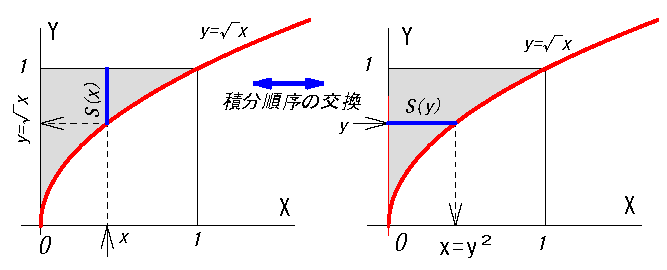
2変数のどちらを先に固定するかにより以下の(ⅰ)と(ⅱ)の2通りあります。
ここでの説明は(ⅰ)の場合でした。

\(S(y)=\int_a^b f(x,y)dx\)
（dx で積分しているが この面積S(y)はy の関数）
そしてその\(S(y)\)を ｙについて [c,d] の範囲で積分すると 立体の体積が求まる。
\(V=\iint_D f(x,y) dxdy\)\(=\int_c^d \underbrace{\int_a^b f(x,y)dx }_{S(y)}\ dy \)… ❶

\(S(x)=\int_c^d f(x,y)dy\)

（dy で積分しているが この面積S(x)はx の関数）

そしてその\(S(x)\)を xについて [a,b] の範囲で積分すると 立体の体積が求まる。
\(V=\iint_D f(x,y) dxdy\) \(=\int_a^b \underbrace{\int_c^d f(x,y)dy }_{S(x)}\ dx \)… ❷

D の定義域の詳細は：
\(D=\{ (x,y)∈R^2 |a≤x≤b,\ h(x)≤y≤g(x)\} \)
「\(D\)は \(y\)について（または\(y\)方向）の縦線集合」ともいう。

このときの積分方法は：
x を固定し、f(x,y) を 積分範囲　\(y=h(x)≤y≤g(x)\) で、y について積分する。
\(S(x)=\int_{h(x)}^{g(x)} f(x,y) dy\)

これをさらに積分範囲　\(a≤x≤b\)で x について積分すると：
\(V=\iint_D f(x,y) dxdy\) \(=\int_a^b \underline{S(x)}\ dx\)\(=\int_a^b \underline{ \int_{h(x)}^{g(x)} f(x,y) dy}\ dx\)…❸

別表記
(この表記では Xについて、yについての積分領域を区別しやすい）
\(V=\int_a^b dx \ \int_{h(x)}^{g(x)} f(x,y) dy \)…❸’

D の定義域の詳細は：
\(D=\{ (x,y)∈R^2 |c≤x≤d,\ \phi(y)≤y≤\psi(y)\} \)

「\(D\)は\(x\)について（または\(x\)方向）の縦線集合」という。
（横線集合ともいう）
このときの積分方法は：
y を固定し、f(x,y) を 積分範囲　\(y=\phi(x)≤y≤\psi(x)\) で、y について積分する。 すなわち：
\(S(y)=\int_{\phi(y)}^{\psi(y)} f(x,y) dx\)

これをさらに積分範囲　\(c≤x≤d\)で y について積分すると：
\(V=\iint_D f(x,y) dxdy\) \(=\int_c^d \underline{S(y)}\ dy\)\(= \int_c^d \underline{\int_{\psi(y)}^{\phi(y)} f(x,y) dx}\ dy\)…❹

上式と別表記
\(V=\int_a^b dy \ \int_{h(x)}^{g(x)} f(x,y) dx \)…❹’

次のD 領域上で有界な関数\(f(x,y\) について

\(D=\{ (x,y)∈R^2 |a≤x≤b,\ h(x)≤y≤g(x)\} \) \(:\color{red}{ⓐ}\)
（\(D\)は\(y\)についての縦線集合）
\(D=\{ (x,y)∈R^2 |c≤y≤d,\ \phi(y)≤x≤\psi(y)\} \) \(:\color{red}{ⓑ}\)
（\(D\)は\(x\)についての縦線集合または横線集合）

のようにD は x とy の両軸についての縦線集合のとき：

\(\iint_D f(x,y) dxdy=\)

\( \int_a^b \int_{h(x)}^{g(x)} f(x,y) dy\ dx \) \(= \int_c^d \int_{\phi(y)}^{\psi(y)} f(x,y) dx\ dy \) …❺

と積分順序が替えられます。
別表記すると：
\(\int_a^b dx \ \int_{h(x)}^{g(x)} f(x,y) dy \) \(=\int_c^d dy \ \int_{\phi(y)}^{\psi(x)} f(x,y) dx \)…❺’

積分順序の交換のメリットは積分の計算が容易になる方法が選べること、
または被積分関数が積分できないが、順序を替えると積分可能となる場合がある。

上記のD 領域より
\( \int_0^3 \ \underline{ \int_0^{2-\frac{2}{3}x} x\ y\ dy\ } \ dx\)

 被積分関数\( x y\) の\(x\) は定数扱いです。　

\( =\int_0^3 \ [\ \frac{1}{2} x\ y^2]_0^{2-\frac{2}{3}x}\ dx\) \(= \int_0^3 \ \frac{1}{9}(2 x^3 -12x^2 +18x^2) \ dx\) \(= \frac{1}{9}\ [\frac{1}{2} x^4 - 4 x^3 +9 x^2\ ]_0^3 \)

\(=\frac{3}{2}\)

まず、例題に対応する領域\(D\) の式を作ります。
y を固定し、そのときのx を求める。（上図 右）
・\(x=3-\frac{3}{2}y\)
・yの区間は[0、2]
これより領域\(D\) は：
\( D= \{ (x,y)| 0≤ y ≤2 ,\quad \underbrace{ 0 ≤ x ≤\ 3-\frac{3}{2}y}_{xの範囲}\} \)

\( \int_0^2 \ \int_0^{3-\frac{3}{2}y} x\ y\ dx\ dy\) \(= \int_0^2 \ [\ \frac{1}{2} y\ x^2\ ]_0^{2-\frac{3}{2}y}\ dy\) \(= \int_0^2 \ \frac{1}{8} ( 9 y^3 - 36y^2 +36y) \ dy\) \(= \frac{1}{8} [\ \frac{9}{4} y^4 - 12 y^3 +18y^2\ ]_0^2 \)

\(= \frac{2}{3}\)

このように積分領域が決まれば、重積分も１変数の定積分に帰着して積分計算するだけです。

上記のD 領域より
\( \int_0^{\frac{1}{2}}\ \int_{2x}^1\ (x+y)\ dy\ dx\)

\(=\int_0^{\frac{1}{2}}\ [xy+\frac{1}{2}y^2]_{2x}^1\ dx\) \(=\int_0^{\frac{1}{2}}\ (-4x^2+x+\frac{1}{2})\ dx\) \(=[-\frac{4}{3}x^3 +\frac{1}{2}x^2+\frac{1}{2}x]_0^{\frac{1}{2}}\ dx\)

\(=\frac{5}{24}\)

まず、例題に対応する領域\(D\) の式を作ります。
y を固定し、そのときのx を求める。（上図 右）
・\(x=\frac{1}{2}y\)
・yの区間は[0、1]
これより領域\(D\)は：
\( D= \{ (x,y)|\ 0≤ y ≤1 ,\quad \underbrace{ 0 ≤ x ≤ \frac{1}{2}y}_{xの範囲} \} \)

\( \int_0^1 \int_0^{\frac{1}{2}y} \ (x+y)\ dx\ dy\)

\(= \int_0^1\ [\frac{1}{2}x^2 + xy]_0^{\frac{1}{2}y}\ dy\) \(= \int_0^1\ \frac{5}{8}y^2 \ dy\) \(= [ \frac{5}{24}y^3]_0^1 \)

\(=\frac{5}{24}\)

☞【ワンポイント】

上記のD 領域より
\( \int_0^1\ \int_{\sqrt x}^1\ (x+y)\ dy\ dx\)

\(=\int_0^1\ [xy+\frac{1}{2}y^2]_{\sqrt x}^1\ dx\) \(=\int_0^1 \ (- x\sqrt x + \frac{1}{2}x +\frac{1}{2})\ dx\) \(=[-\frac{2}{5}x^{\frac{5}{2}} + \frac{1}{4}x^2 +\frac{1}{2}x]_0^1 \)

\(=\frac{7}{20}\)

まず、例題に対応する領域\(D\) の式を作ります。
y を固定し、そのときのx を求める。（上図 右）
・\(x=y^2\)
・yの区間は[0、1]
これより領域\(D\)は：
\( D= \{ (x,y)|\ 0≤ y ≤1 ,\quad \underbrace{ 0 ≤ x ≤ y^2}_{xの範囲} \} \)

\( \int_0^1 \int_0^{y^2} \ (x+y)\ dx\ dy\)

\(= \int_0^1\ [\frac{1}{2}x^2 + xy]_0^{y^2}\ dy\) \(= \int_0^1\ (\frac{1}{2}y^4+y^3)\ dy\) \(= [ \frac{1}{10}y^5+ \frac{1}{4}y^4]_0^1 \)

\(=\frac{7}{20}\)

積分領域が長方形（各辺がx軸とy軸に平行）、すなわち
\(\quad D=[a,b] \times [c,d]\) であり、

D 上の関数\(f(x,y)\)、 [a,b]上の関数\(g(x)\)、 [c,d]上の関数\(h(y)\) はそれぞれ連続ならば：

\(\iint_D f(x,y) dxdy\)\(=\left( \int_a^b g(x)\right) \) \(\left( \int_c^d h(y) \right) \)

∗\(f(x,y)=e^{x+y}=e^x e^y \)
\(\iint_D e^{x+y} dxdy\) \(= \iint_D e^x e^y dxdy \) \(= \int_a^b e^x dx \int_c^d e^y dy\)

∗\(f(x,y)=x^j\ y^k \)
\(\iint_D x^j\ y^k dxdy\) \(= \int_a^b x^j dx \int_c^d y^k dy\)

前の講義の中で面積確定が重積分の可積分か否かの条件である述べました。
平面上の有界閉区間\(D\)において被積分関数\(f(x,y)=1\) の重積分は「面積をもつ」という。
\(\iint_D f(x,y) dx dy\)\(=\iint_D dx dy\)
( \(=\iint_D 1 \cdot dx dy\) )

これは有界閉区間\(D\)の面積である。（∵高さ「1」の体積だから）
今までの例題に\(f(x,y)=1\)とすれば「有界閉区間\(D\)の面積が求まる」
 …これが「面積をもつ」ということです。