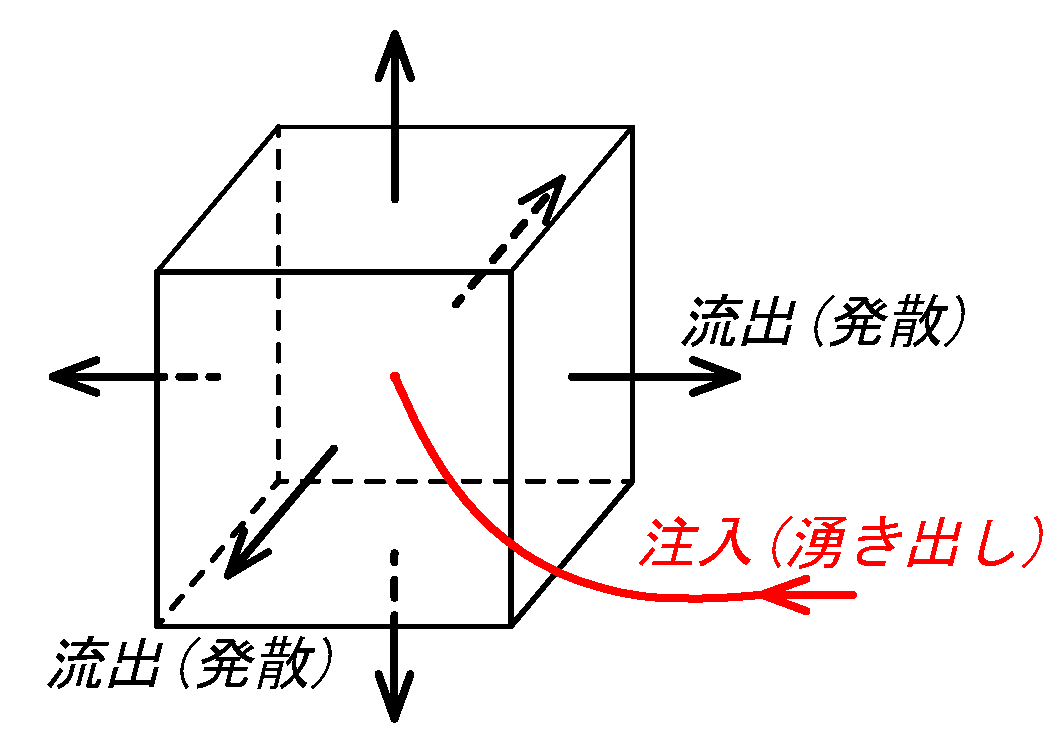
\(div \bv{A}=div (A_x,A_y,A_z)\) \(=∇\cdot (A_x,A_y,A_z)\)
\(=\dspder{A_x}{x}+\dspder{A_y}{y}+\dspder{A_z}{z}\)
\(\dsiii_V div \bv{A} dV\)\(=\dsiii_V (\dspder{A_x}{x}+\dspder{A_y}{y}+\dspder{A_z}{z})dxdydz\)
\(\ \scriptsize {:Ⓐ}\)
\(dS=\sqrt{(\pder{z}{x})^2+ (\pder{z}{y})^2 + 1\ }\ dxdy\)
\(\ \scriptsize {(❺-1)}\)
\(dS=|\dspder{r}{x} \x \dspder{r}{y}|dx dy\)
\(\ \scriptsize {(❺-1')}\)
\(dS=\dsfr{1}{|cosα|}dydz\)\(=\dsfr{1}{|cosβ|}dzdx\)\(=\dsfr{1}{|cosγ|}dxdy\)
\(\ \scriptsize {:❼-1}\)
\(\dsiii_V \scriptsize { (\dspder{A_x}{x}+\dspder{A_y}{y}+\dspder{A_z}{z})} dxdydz\)
\(=\dsii_S \scriptsize { (A_x cosα+ A_ycosβ + A_z cosγ)} dS \)
この式を以下の3式に分解する
\( \dsiii_V \dspder{A_x}{x} dxdydz=\dsii_S A_x cosα dS\) \(\ \scriptsize {:©_1}\)
\( \dsiii_V \dspder{A_y}{y} dxdydz=\dsii_S A_y cosβ dS\) \(\ \scriptsize {:©_2}\)
\( \ul{ \dsiii_V \dspder{A_x}{z}dxdydz =\dsii_S A_z cosγ dS }\) \(\ \scriptsize {:©_3}\)
\(\dsiii_V \small{A_x}{z}dxdydz=\dsii_D \ul{ \{ \dsi_{z_1}^{z_2}\dspder{A_x}{z}dz\} } dxdy \)
下線部の答えは,\(A_z\)のzでの偏微分をz で積分しているから\(A_z\)です。
すなわち
\([A_z]_{z_1}^{z_2}\)\(=A_z(x,y,z_1)-A_z(x,y,z_2)\)
\(\dsiii_V \dspder{A_x}{z}dxdydz\)\(=\dsii_D \ul{(A_z(x,y,z_1)-A_z(x,y,z_2))}dxdy\)
\(\ \scriptsize {:Ⓓ}\)
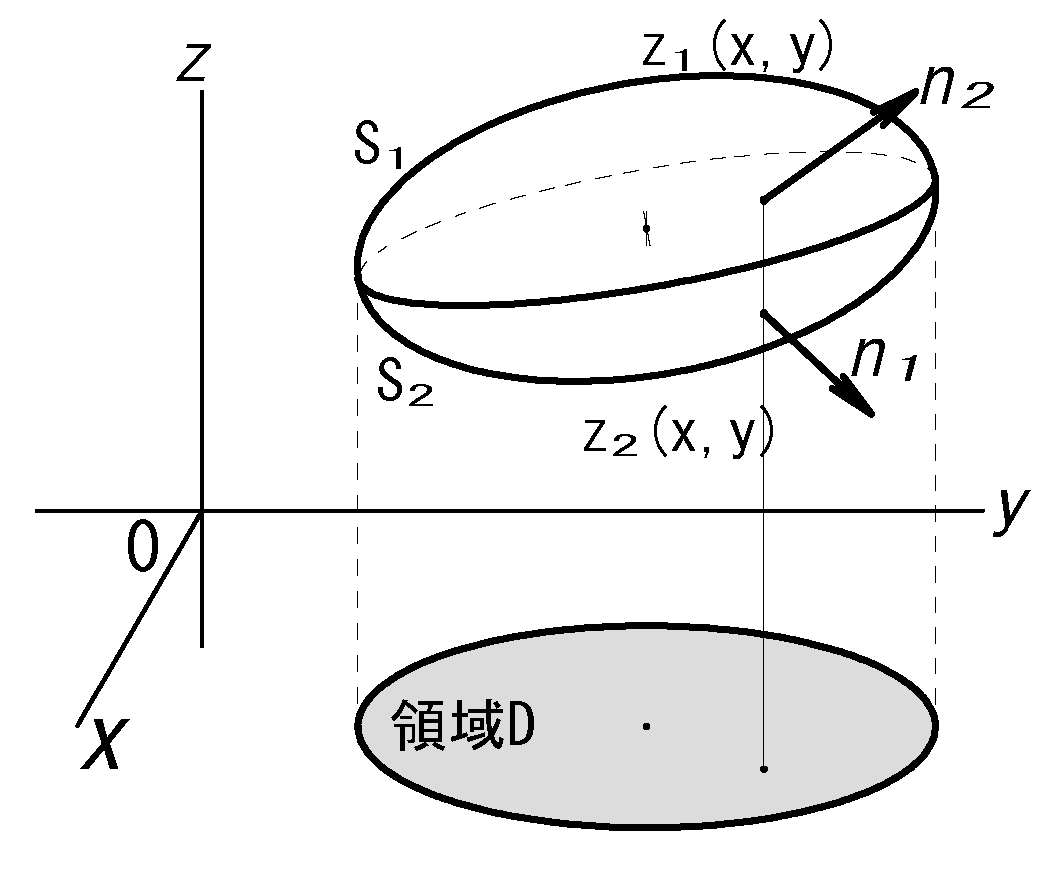
ここで面素dS、単位法線ベクトルnの表記を思い出そう。
曲面S:\(S(x,y)=S(x,y,z(x,y))\)とすると
\(\dspder{S}{x}=(1,0,\dspder{z}{x})\) \(\to \) \( S'_x=(1,0,z'_x)\)
\(\dspder{S}{y}=(0,1,\dspder{z}{y})\) \(\to \) \( S'_y=(1,0,z'_y)\)
以下は外積計算です。
☞
ベクトルの外積の
【参照先】
\(C=\dspder{S}{x}\x\dspder{S}{y}=S'_x \x S'y \)
\(C=(1,0,z'_x)\x (1,0,z'_y)\) \(=(-\dspder{z}{x},-\dspder{z}{y},1)\) \(=(-z'_x,-z'_y,1)\)
上記の参照式\(\ \scriptsize {(❺-1)(❺-1')}\)より
\(|C|=|\dspder{S}{x}\x\dspder{S}{y}|\)\(= \sqrt{ (\dspder{z}{x})^2+(\dspder{z}{y})^2+1}\)
\(=\sqrt{(z'_x)^2+(z'_y)^2+1} \)
\(\bv{n}=(n_x,n_y,n_z)\) として
\(\bv{n}=\dsfr{-\dspder{z}{x},-\dspder{z}{y},1}{|\dspder{S}{x}\x\dspder{S}{y}|}\)
\(=\dsfr{C}{|C|}=\dsfr{(-z'_x,-z'_y,1)}{\sqrt{(z'_x)^2+(z'_y)^2+1}}\)
\(=(\dsfr{-z'_x}{|C|},\dsfr{-z'_y}{|C|},\dsfr{1}{|C|})\)
注:この式はベクトルの成分表示
\(n_z=\dsfr{1}{|C|}=\dsfr{1}{\sqrt{(z'_x)^2+(z'_y)^2+1}}\)
上式に\(|C|=|\dspder{S}{x}\x\dspder{S}{y}|\)\(=\sqrt{(z'_x)^2+(z'_y)^2+1} \)を掛ける
\(|\dspder{S}{x}\x\dspder{S}{y}|n_z\)
\(=\dsfr{(\sqrt{(z'_x)^2+(z'_y)^2+1})}{\sqrt{(z'_x)^2+(z'_y)^2+1}}\)
上式の右辺は1 となる。
\(|\dspder{S}{x}\x\dspder{S}{y}|n_z=|C|n_z=1\)
ここで\(\bv{n}_1\)と\(\bv{n}_2\)は次式で表せる:
\(\bv{n}_1=\dsfr{(-z'_{1x},-z'_{1y},1)}{\sqrt{(z'_{1x})^2+(z'_{1y})^2+1}}\)
\(\bv{n}_2=\dsfr{(-z'_{2x},-z'_{2y},1)}{\sqrt{(z'_{2x})^2+(z'_{2y})^2+1}}\)
\(\bv{n}_1\)と\(\bv{n}_2\)は上記の\(\bv{n}\)と同じだから次が言える
\(|\dspder{S}{x}\x\dspder{S}{y}|n_{z1}=|C_1|n_{z1}=1\)
\(|\dspder{S}{x}\x\dspder{S}{y}|n_{z2}=|C_2|n_{z2}=1\)
これから先に学んだ単位法線ベクトルnと 面素dS を登場させる:
\(\bv{n}=(cosα,cosβ,cosγ)\) \(\ \scriptsize {:❷-3}\)
\(dS=|\dspder{r}{x} \x \dspder{r}{y}|dx dy\)
\(\ \scriptsize {(❺-1')}\)
ここでz=rとすれば
\(dS=|\dspder{z}{x} \x \dspder{z}{y}|dx dy=|C||dx dy\)
これより
\(|C_1|n_{z1}=cosγ_1|C_1| =1\)
\(|C_2|n_{z2}=cosγ_2|C_2| =1\)
上式の結果が1 であることが重要,何かに1をかけてもその何かは変わらない。
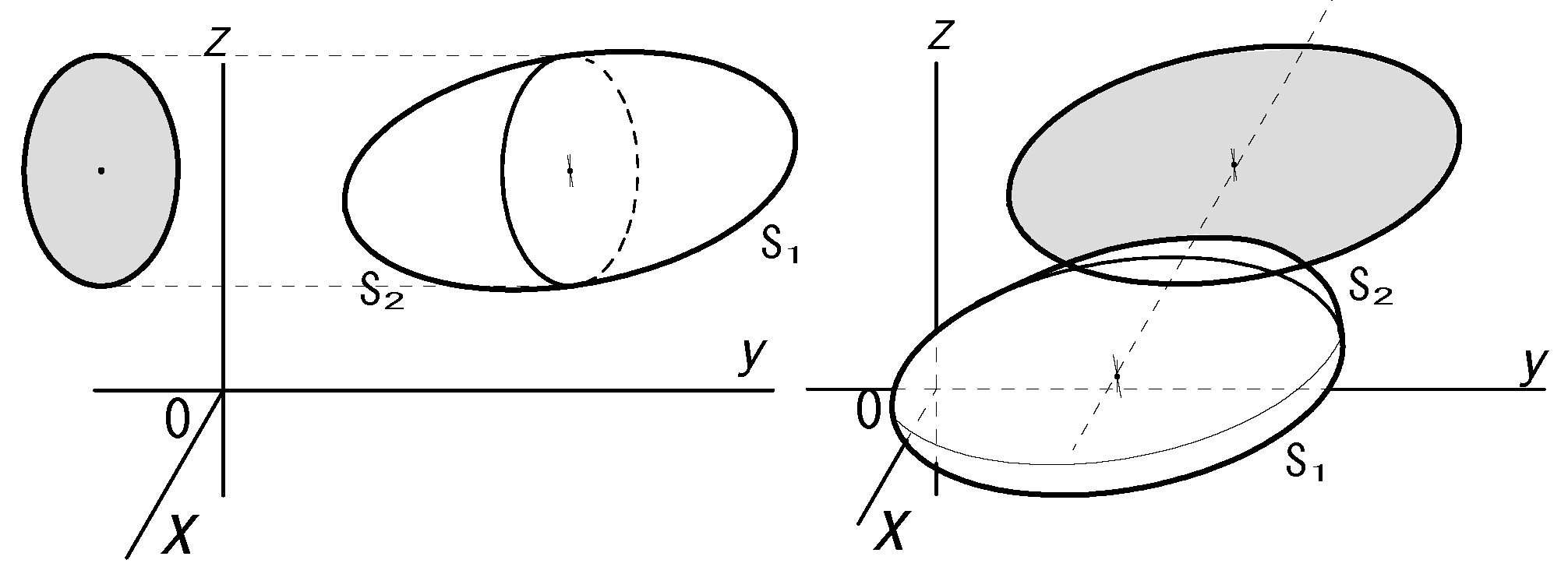
fig2から\(γ_1\) は鋭角、\(γ_2\)は鈍角であるから\(cosγ_1\)は正、\(cosγ_2\) は負であるから:
\(γ\)は法線がz軸となす角です。
\(\dsiii_V \dspder{A_x}{z}dxdydz\)\(=\dsii_D (A_z(x,y,z_1)-A_z(x,y,z_2))dxdy\)
\(\ \scriptsize {:Ⓓ}\)
以下は各項に\(|C_n||dx dy=1\)をかけているのがポイント。
まず1番目の項:
\(\dsii_D A_z(x,y,z_1)dxdy\)\(=\dsii_D A_z(x,y,z_1)\underbrace{cosγ_1 |C_1|}_{=1}dxdy\)
\(=\dsii_D A_z(x,y,z_1)cosγ_1 \underbrace{dS_1}_{|C_1||dx dy}\)
同様にして(但し\(cosγ_2\)は負に配慮)
\(\dsii_D -A_z(x,y,z_2)dxdy\)
\(=\dsii_{S_2} A_z(x,y,z_1) \underbrace{cosγ_2 |C_2|}_{=1}dxdy\)
\(=\dsii_{S_2} A_z(x,y,z_1) \underbrace{cosγ_1 |C_1|}_{=1}dxdy\)
\(=\dsii_{S_2} A_z(x,y,z_2)cosγ_1 \underbrace{dS_1}_{|C_1||dx dy}\)
従って
\(\dsiii_V \dspder{A_x}{z}dxdydz\)\(=\dsii_{S_1} A_z(x,y,z_1)cosγ_1 dS_1\)
\(+\dsii_{S_2} A_z(x,y,z_2)cosγ_1 dS_1\)
上下の積分を1つにまとめると(積分領域をSに、面素をdSにまとめる)
\(\dsiii_V \dspder{A_x}{z}dxdydz\)\(=\dsii_S A_z(x,y,z_1)cosγ_1 dS\) \(=\dsii_S A_z cosγ_1 dS\)
\(\ \scriptsize {:©_3}\)
©_3 が求まりました。 同様にして©_1,©_2 が導出できます。
\( \dsiii_V \dspder{A_x}{x} dxdydz=\dsii_S A_x cosα dS\) \(\ \scriptsize {:©_1}\)
\( \dsiii_V \dspder{A_y}{y} dxdydz=\dsii_S A_y cosβ dS\) \(\ \scriptsize {:©_2}\)
以上の結果より公式❶になる確認をしてみよう
\(\ul{\dsiii_V div \bv{A} dV} \)\(=\dsiii_V (\dspder{A_x}{x}+\dspder{A_y}{y}+\dspder{A_z}{z})dxdydz\)
(式Ⓐ)
\(=\dsii_S A_z cosγ_1 dS\)\(+\dsii_S A_x cosα dS\)\(+\dsii_S A_y cosβ dS\)
\(=\dsii_S (A_x cosα+ A_ycosβ + A_z cosγ) dS \)
\(=\dsii_S (A_x,A_y,A_z) \cdot (cosα,cosβ,cosγ) dS\)
\(=\ul{\dsii_S \bv{A}\cdot \bv{n}dS}\)
(式Ⓑ)
\(\therefore \ul{\dsiii_V div \bv{A} dV} \)\(=\ul{\dsii_S \bv{A}\cdot \bv{n}dS}\)