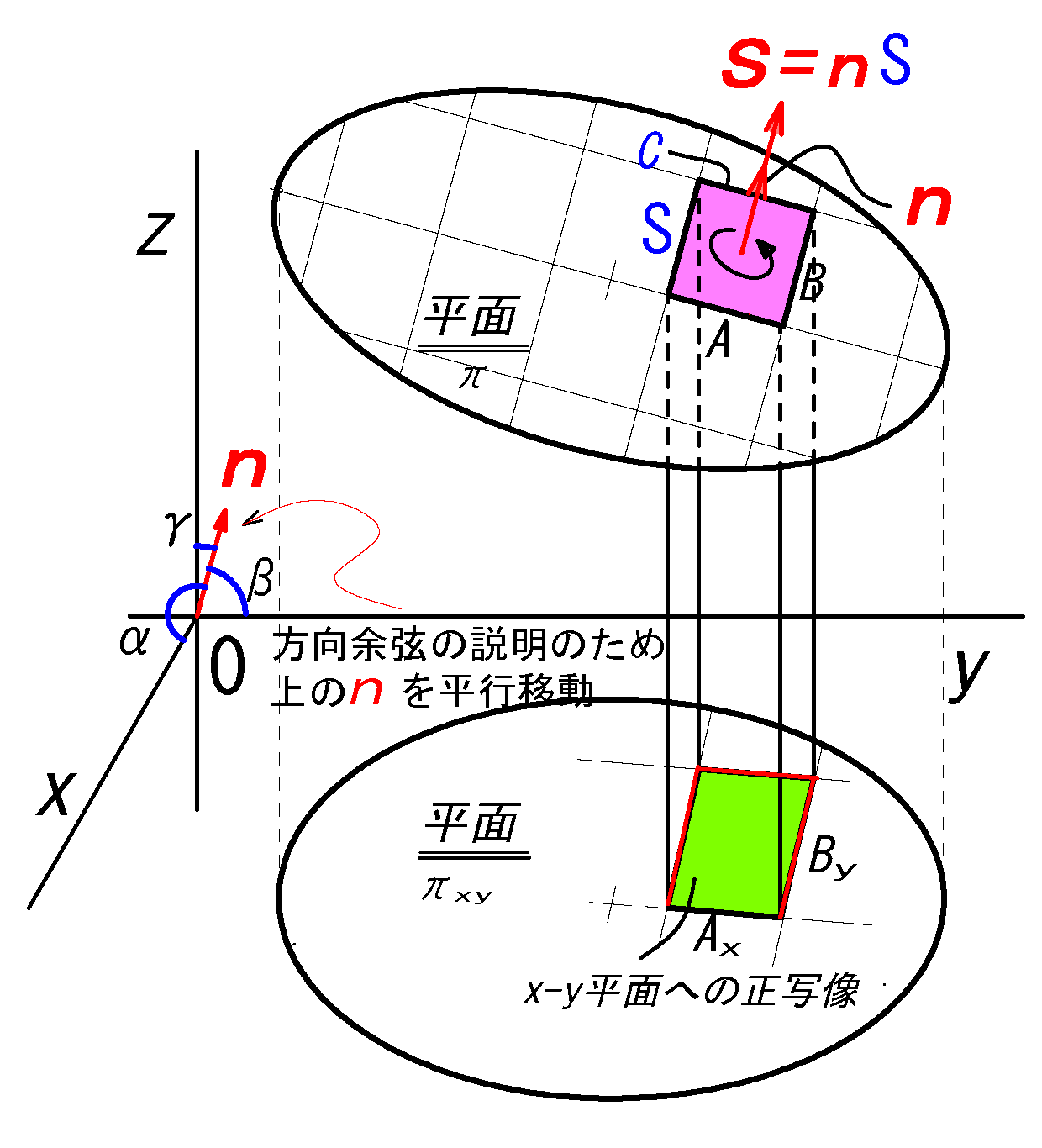
\(\bv{S}=\bv{n}S\) \(\ \scriptsize {:❶-1}\)
また面積ベクトルはベクトル AとBの外積でもある。
\(\bv{S}=\bv{A} \x \bv{B}\)
fig1の回転方向にともなう右ねじの方向に進む方向が正の方向です。
・これは面積ベクトルの3面(xyz座標軸が作る面)への正写像です。
・fig1 は Sのx-y平面への写像した例です。
\(\dsfr{dr(t)}{dt}\)\(=r'(t)\)\(=\displaystyle \lim_{Δt \to 0} \dsfr{r(t+Δt)-r(t)}{Δt}\)
これは曲線上のある点\(P_n\)の接線ベクトルです。
曲線のある点の近似は接線です。
曲線のある範囲(長さ)においてその分割数n を無限に大きくして、Δtを無限に小さく \(Δt \to 0\) の極限の次式
は曲線の長さを与える。
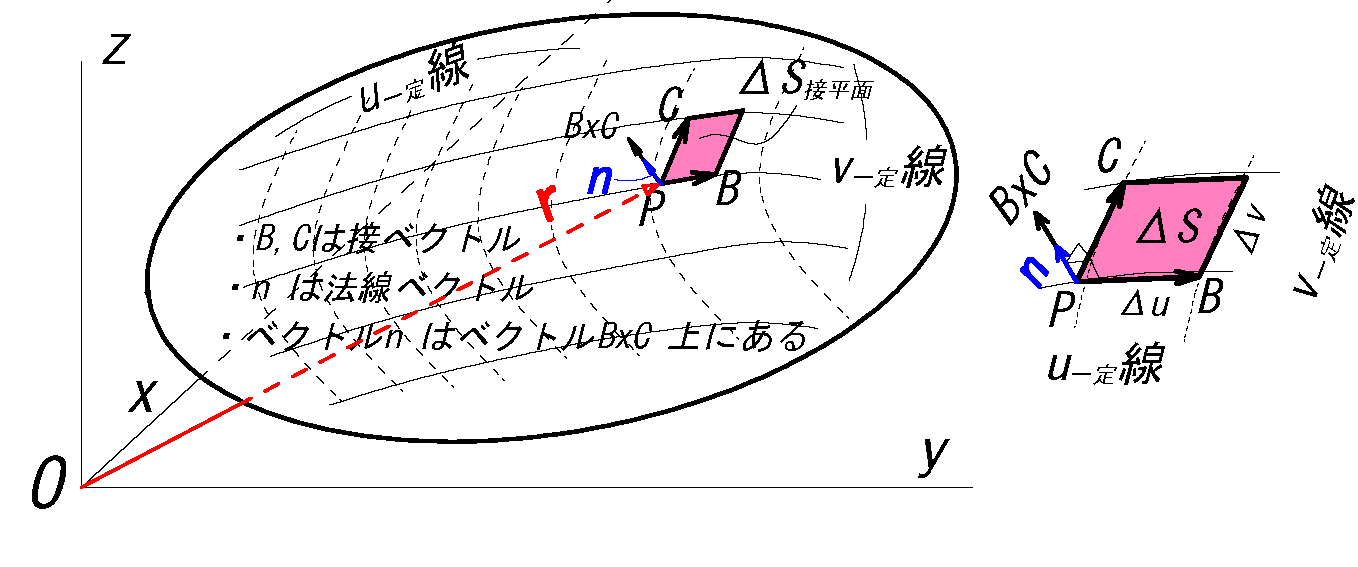
(直交座標成分表示では: \(\bv{r}=(x(u,v),y(u,v),z(u,v))\) )
曲面の面積は次式で与えられる
\(S=\dsii_S \underline{dS}\)
\(=\dsii_D \underline{ |\pder{\bv{r}}{u} \x \pder{\bv{r}}{v} | \ dudv } \)
\(\ \scriptsize {:❹-1}\)
\(dS=|\dspder{r}{u} \x \dspder{r}{v}|dudv \) \(\ \scriptsize {:❹-2}\)
\(dS(\Delta S)\)は後述しますが、面素または面要素,面積素などという。
\(r(u,v)\) \(\ , \) \(r(u+Δ,v)\) \(\ , \) \(r(u+Δu,v+Δv)\) \(\ , \) \(r(u,v+Δv)\)
\(\bv{B}=r(u+Δu,v)-r(u,v)\) \(\ , \) \(\bv{C}=r(u,v+Δv)-r(u,v)\)
\(ΔS=|\bv{B}\x \bv{C}|\)
\(=|[r(u+Δu,v)-r(u,v)] \times [r(u,v+Δv)-r(u,v)]| \)
\(=|\dsfr{r(u+Δu,v)-r(u,v)} {\color{blue}{Δu}}\)
\(\times \dsfr{r(u,v+Δv)-r(u,v)} {\color{blue}{Δv}}|\color{blue}{ΔuΔv}\)
\(Δu,Δv \to 0\) にして:
\(=|\pder{r}{u} \x \pder{r}{v}|dudv \)
\(\therefore dS=|\dspder{r}{u} \x \dspder{r}{v}|dudv \) \(\ \scriptsize {(❹-2)}\)
\(S=\dsii_S \underline{dS}\) \(=\dsii_D \underline{ |\pder{\bv{r}}{u} \x \pder{\bv{r}}{v} | \ dudv } \) \(\ \scriptsize {(❹-1)}\)
\(\bv{B}=\dspder{\bv{r}}{u}\Delta u\) \(,\quad \) \(\bv{\bv{C}}=\dspder{\bv{r}}{v}\Delta v\)
(偏微分の項はベクトルの傾き)
\(\Delta S=|\bv{B} \x \bv{C}|\)\(=|\dspder{r}{u}\Delta u \x \dspder{r}{v}\Delta v|\)
\(=|\dspder{r}{u} \x \dspder{r}{v}|\Delta u \Delta v\)
(※1)
\(S=\dsii_S \underline{dS}\) \(=\dsii_D \underline{ |\pder{\bv{r}}{u} \x \pder{\bv{r}}{v} | \ dudv } \) \(\ \scriptsize {(:❹-1)}\)
導出(1)より簡潔に導き出せましたね。
(※1)外積の性質から\(\Delta u\ \Delta v \) は正のスカラーだから絶対値の外に出せる。
外積の結合法則 \(k\bv{A}\x \bv{B}=k(\bv{A}\x\ \bv{B})\)(\(k\):スカラー)
\(\bv{n}=\dsfr{1} {| \pder{\bv{r}}{u} \x \pder{\bv{r}}{v} |}
\pder{\bv{r}}{u} \x \pder{\bv{r}}{v} \) \(\ \scriptsize{❹-3}\)
\(\pder{r}{x}=\pder{}{x}(x,y,z(x,y)) \) \(=(1,0,z_x)\)
\(\pder{r}{y}=\pder{}{x}(x,y,z(x,y)) \) \(=(0,1,z_y)\)
\(\pder{r}{z}=\pder{}{x}(x,y,z(x,y)) \) \(=(0,0,1)\)
\(\pder{\bv{r}}{x} \x \pder{\bv{r}}{y} \)
\(=\left(
\begin{array}{c}
1\\
0\\
z_x
\end{array}
\right)
\) \( \x \)
\( \left(
\begin{array}{c}
0 \\
1 \\
Z_y
\end{array}
\right)
\)
\(=\left(
\begin{array}{c}
-z_x\\
-z_y\\
1
\end{array}
\right)
\)
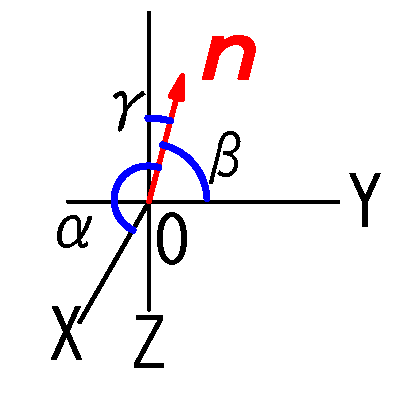
\(\bv{n}=(cosα,cosβ,cosγ)\) \(\ \scriptsize {:❷-3}\)
\(S=\dsii_S dS\)
\(=\dsii_D \sqrt{(\pder{z}{x})^2+ (\pder{z}{y})^2 + 1\ }\ dxdy\) \(\ \scriptsize {:❺-1}\)
\(\pder{\bv{r}}{x} \x \pder{\bv{r}}{y}\)
\(=\left(
\begin{array}{c}
1\\
0\\
z_x
\end{array}
\right)
\)
\( \x \)
\( \left(
\begin{array}{c}
0 \\
1 \\
Z_y
\end{array}
\right)
\)
\(=\left(
\begin{array}{c}
-z_x\\
-z_y\\
1
\end{array}
\right)
\)
\(\therefore\) \(|\pder{\bv{r}}{x} \x \pder{\bv{r}}{y}|\)\(=\sqrt{z_x^2+z_y^2+1}\)
\( \dsii_S dS\)
\(=\dsii_D \sqrt{(\pder{z}{x})^2+ (\pder{z}{y})^2 + 1\ }\ dxdy\)
\(\ \scriptsize {(❺-1)}\)
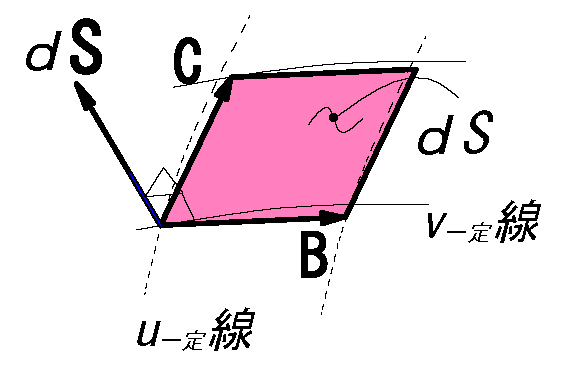
曲面:\(\bv{r}=(u,v)\)として:
\(\bv{dS}=\bv{n} dS\)
\(=\dsfr{ \pder{\bv{r}}{u} \x \pder{\bv{r}}{v} } {| \pder{\bv{r}}{u} \x \pder{\bv{r}}{v} |} \)
\(|\dspder{r}{u} \x \dspder{p}{v}|du dv\)
\(=\pder{\bv{r}}{u} \x \pder{\bv{r}}{v} du dv\) \(\ \scriptsize {:❻-2}\)
\(\bv{n}=(cosα,sinβ,sinγ)\) \(( \scriptsize {❷-1より})\)
\(\bv{dS}=\bv{n} dS\)\(=(cosα,cosβ,cosγ)dS\)\(=(cosα dS ,cosβ dS,cosγ dS)\)
\(\bv{dS}\)の成分は次の座標軸平面に分かれ(左から) y-z軸平面,z-x軸平面,x-y軸平面に正写像される。
( \(\bv{dS}\) は微小な平行四辺形、その写像も\(n\)と同様である。)
\(\therefore \)
\(\bv{dS}=(\underbrace{cosα dS}_{yz写像} ,\underbrace{cosβ dS}_{zx写像},\underbrace{cosγ dS}_{xy写像})\)
余弦(cos)の負となる対応のため絶対値がつく
\(dydz=|cosα|dS\)\(, \ \) \(dzdx=|cosβ| dS\)\(, \ \) \(dxdy=|cosγ| dS\)
\(\ \scriptsize {:❻-3}\)
\(\bv{dS}=( \pm cosα dS, \pm cosβ dS, \pm cosγ dS )\)
\(=( \pm dydz, \pm dzdx, \pm dxdy)\) \(\ \scriptsize {:❻-4}\)
dydz, dzdx, dxdy は面素dSの成分です
ここでは媒介変数u,v を使うのでヤコビアン\(J\)により変数変換します。
☞
ヤコビアンの【参照先】
\(dxdy=J_{xy}\ dudv=\left|\dspder{(x,y)}{(u,v)} \right|dudv\)【※】
\(dydz=J_{yz}\ dudv=\left|\dspder{(y,z)}{(u,v)} \right|dudv\)
\(dzdx=J_{zx}\ dudv=\left|\dspder{(z,x)}{(u,v)} \right|dudv\)
\(\cdots \cdots \scriptsize {:❻-5}\)
ヤコビアンの例:\(J_{xy}\)【※】
\(J_{xy}=\pder{(x,y)}{(u,v)}\)
\(=
\begin{vmatrix}
\pder{x}{u} & \pder{x}{v} \\
\pder{y}{u} & \pder{y}{v}
\end{vmatrix}
\)
\(=\pder{x}{u}\pder{y}{v} - \pder{x}{v} \pder{y}{u}\)
\(\bv{dS}=( \pm dydz, \pm dzdx, \pm dxdy)\)
\(=( J_{yz} dudv, J_{zx} dudv, J_{xy} dudv)\)
\(\ \scriptsize {:❻-6}\)
曲面:\(\bv{r}=(u,v)\)として:
\(dS=|\dspder{r}{u} \x \dspder{r}{v}|du dv\)\(\ \scriptsize {(❹-2)}\)
曲面:\(z(x,y)\), \(\bv{r}=(x,y,z(x,y)) \)として
\(dS=\sqrt{(\pder{z}{x})^2+ (\pder{z}{y})^2 + 1\ }\ dxdy\)
\(\ \scriptsize {(❺-1)}\)
別表示すると
\(dS=|\dspder{r}{x} \x \dspder{r}{y}|dx dy\)
\(\ \scriptsize {(❺-1')}\)
\(dydz=|cosα|dS\)\(, \ \) \(dzdx=|cosβ| dS\)\(, \ \) \(dxdy=|cosγ| dS\)
\(dS=\dsfr{1}{|cosα|}dydz\)\(=\dsfr{1}{|cosβ|}dzdx\)\(=\dsfr{1}{|cosγ|}dxdy\)
\(\ \scriptsize {:❼-1}\)
