∗ベクトル場の回転の定義
∗回転の式❶’の導出
∗回転の物理的な意味
∗回転rotの例
∗ 例題：ベクトルの回転を求める

∗【閑話】電場の回転の式❹の導出

 今回は「ナブラ∇ とベクトルA の外積」である「\(∇\x \bv{f}\)」で表せるベクトルの回転「\( rot\ \bv{f}　\)」 を学びます。
回転(rot)は流体の渦の強さと方向を表します。
（ここでは渦を引用して説明しています。）
電磁気学での例は（【参照先】)を見てください。

今まで学んだ勾配と発散を書くと：
（いずれもナブラ記号∇を使った演算である）
・勾配：\(grad\ \bv{f}=\ul{∇\ f}　\) \(=(\pder{f(x,y)}{x},\pder{f(x,y)}{y},\pder{f(x,y)}{z}) \)

（ スカラー\( f \) から ベクトルに変換している）

・発散：\(div\ \bv{f}= \ul{∇\cdot \bv{f}}\) \(=\pder{}{x}f_x+\pder{}{y}f_y+\pder{}{z}f_z\)

（ ベクトル\( \bv{f} \) から スカラーに変換している）

今回学ぶのは "rotation"：
・回転：\(\color{blue}{rot\ \bv{f}=\ul{ ∇\x \bv{f}}}\) \(\color{blue}{= (\pder{f_z}{y}-\pder{f_y}{z},} \) \(\color{blue}{\pder{f_x}{z}-\pder{f_z}{x},} \) \(\color{blue}{\pder{f_y}{x}-\pder{f_y}{y} )} \)

（ ベクトル\( \bv{f} \)場から ベクトル場に対応 ）

上記の３式の違いの流れを見ると面白いです。
\(　∇\ f\to∇\cdot \bv{f}\to∇\x \bv{f}\)
∇式の御三家みたいですね。

ベクトルの場の回転  

(※):式❶' の導出　

\(∇=(\pder{}{x},\pder{}{y},\pder{}{z})\)
\(\bv{f}=( f_x ,f_y ,f_z)\)　（変数は省略）　
\(\underline{ rot \bv{f} \ }=∇ \x \bv{f}\) \(=(\pder{}{x},\pder{}{y},\pder{}{z}) \x ( f_x ,f_y ,f_z)\)　Ⓧ続く
 ベクトルの外積の【参考先】

参考:ベクトルの外積の演算方法：
ベクトル\(a\)と\(b\)のベクトルの外積（ベクトル積、クロス積ともいう）は以下となる。
\(a= \left( \begin{array}{c} a_1 \\ a_2 \\ a_3 \end{array} \right) \) \(,\) \(b= \left( \begin{array}{c} b_1 \\ b_2 \\ b_3 \end{array} \right) \) とすると：
\(a \times b=\) \( \left( \begin{array}{c} a_2 b_3 - a_3 b_2 \\ a_3 b_1 - a_1 b_3 \\ a_1 b_2 - a_2 b_1 \end{array} \right) \)

Ⓧの続き:
上記を参考にして、ベクトルを以下のように縦行列に表示すると外積計算しやすい

\(=\left( \begin{array}{c} \pder{}{x}\\ \pder{}{y}\\ \pder{}{z} \end{array} \right) \) \( \x \) \( \left( \begin{array}{c} f_x \\ f_y \\ f_z \end{array} \right) \) \(= \left( \begin{array}{c} \pder{f_z}{y}-\pder{f_y}{z}\\ \pder{f_x}{z}-\pder{f_z}{x}\\ \pder{f_y}{x}-\pder{f_x}{y} \end{array} \right) \)

\(\therefore 式 ①=①'　\)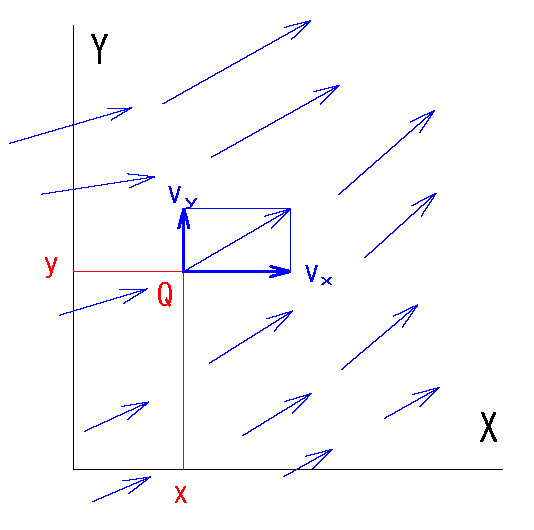

速度\(V\)に対しｘ軸方向の速度成分を\(V_x\) 、 y軸方向の速度成分を\(V_y\)とする。
簡単のため、z軸を一定にしたｘｙ平面の２次元での速度ベクトル場\((V_x,V_y) \)を考えます。
 fig1　の速度ベクトル場において点Q での速度ベクトル\(V(V_x,V_y) \)を表し、点Q に置かれた葉っぱ が速度ベクトルにより回転しながら流れていくイメージをして下さい。(この回転について考える)

・葉っぱ が回転しながら流れるときは「渦がある」といい、\(rot \bv{V} \ne 0\) である。
・葉っぱ が回転しないときは「渦がない」といい、\(rot \bv{V} = 0\) である。　
・\(rot \bv{V}\) は渦の強さを示している。

 fig2 では葉っぱ ではなく、簡単のため x 軸に平行な棒（長さ\(Δx\)）、y 軸に平行な棒（長さ\(Δy\)）を置き、速度\(V\) のx成分の\(V_x\)　と y成分の\(V_y\)がどのように 回転に対し、作用するかを調べていきます。
ここでの回転は反時計方向を正とする。(右手系を使う)【参照先】
fig2 の左下の図【 x 軸に平行な長さΔx の棒】回転:
\(Δx\)棒の回転にはy軸方向の速度\(V_y\)が作用し、ｘ軸方向の速度\(V_x\)は回転には寄与しない。
点Qには\(V_y(x,y)\)、点Aには\(V_y(x+Δx,y)\)が作用するので、\(Δx\)棒の点Aは\(V_y(x+Δx,y)-V_y(x,y)\)の分、先に進む…すなわち回転する。　　　　　
以下は円運動の角速度 \(ω=\frac{v}{r}\)　(半径r、周束度v)を留意する。
Q を中心に A が回転し、その単位時間当たりの回転角\(θ_y\)(rad)は：
\(θ_y\)\(=\frac{V_y(x+Δx,y)-V_y(x,y)}{Δx}\)

上式を微分すると、回転作用となる渦の強さ\(A_y\) が求まる。
全体的には3次元を考えているので偏微分となる
\(A_y=\displaystyle \lim_{ Δx \to \infty } \frac{V_y(x+Δx,y)-V_y(x,y)}{Δx}\) \(=\pder{V_y}{x}\)　\(\ :❷\)　

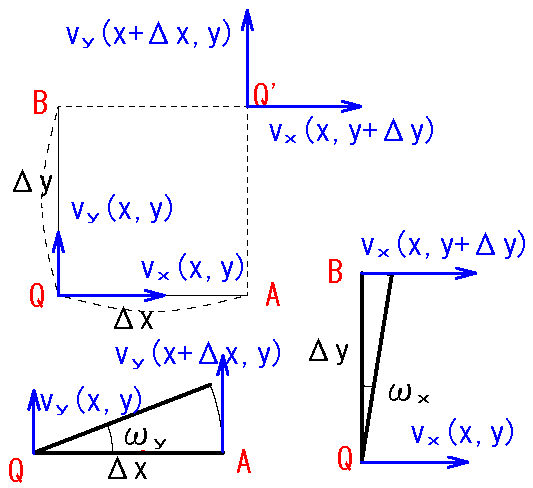
fig2 の右下の図【 y 軸に平行な長さΔy の棒】回転:
「\(Δx\)棒」の回転と同様にして\(Δy\)棒の回転は、Q を中心に B が回転し、その単位時間当たりの回転角\(θ_x\)(rad)は：
回転角は反時計方向が正だから \(V_x(x,y+Δy)-V_y(x,y)\)が正なら、回転角は負であるので

\(θ_x=-\frac{V_x(x,y+Δy)-V_y(x,y)}{Δy}\)
\(A_x=-\displaystyle \lim_{ Δx \to \infty } \frac{V_x(x,y+Δy)-V_y(x,y)}{Δy}\) \(=-\pder{V_x}{y}\)\(\ :❸\)

x成分の\(V_x\)によるうずの強さ\(A_y=❷\)と y成分の\(V_y\)によるうずの強さ\(A_x=❸\)を合成（❷+❸）すると：
\(\bv{K_z}=\bv{A_y}+\bv{A_x}=\underline{ \pder{V_y}{x} -\pder{V_x}{y} }\)

下線部は先述の「ベクトル場の回転式❶」の x成分です。(ベクトルの記号が異なるが)
これは下図のように「xy 平面」の点Q を通るz軸に平行な直線(xy平面の垂線)を中心に回転するうずの強さ\(K_z\) です。
このベクトルを3次元で表すと:
「xy 平面」：\(\bv{K_z}\)
\((0,0,K_z)\)\(=(0,0,\pder{V_y}{x} -\pder{V_x}{y})\)

同様にして「yz 平面」の \(\bv{K_x}\) と 「zx 平面」の \(\bv{K_y}\)は次のようになる。
「yz 平面」：\(\bv{K_x}\)
\((K_x,0,0)\)\(=(\pder{V_x}{y} -\pder{V_y}{z},0,0)\)

「zx 平面」：\(\bv{K_y}\)
\((0,K_y,0)\)\(=(0,\pder{V_x}{z} -\pder{V_z}{x},0)\)

以上を合成すれば、ベクトル場の回転の式❶ が導出できる。

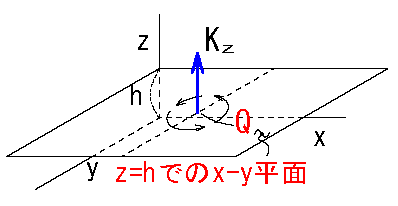
\( rot\ \bv{f}\)\(=(K_x,k_y,k_z)\)
\( rot\ \bv{f}\)\(= (\pder{f_z}{y}-\pder{f_y}{z},\ \)\(\pder{f_x}{z}-\pder{f_z}{x},\ \)\( \pder{f_y}{x}-\pder{f_x}{y}\ )\) \(\ :❶\)

以下は「磁場\(\bv{B}\) の時間変化が電場\(\bv{E}\) の回転を作る」式です。
(電場\(\bv{B}\) の渦ともいえる)
電磁気学のマックウェル方程式の1 つである。
\(∇\x \bv{E} = -\pder{\bv{B}}{t}\) \(\ :❹\)
右辺は「-」だから、磁場\(\bv{B}\)が上向きのとき電場\(\bv{E}\)の回転は時計方向です。

以下のAをベクトルポテンシャルといいます。
 \(\bv{B}=rot\ \bv{A} =∇ \x \bv{A}\)
また次の式が成り立ちます。
 \(rot\bv{B}=∇ \x \bv{B} =μ_0\bv{ｊ}\)
 \(μ_0\bv{ｊ}=∇\x(∇\x \bv{A})=∇^2\bv{A}\)
(\(μ_0\):真空中の透磁率)
磁場\(\bv{B}\)はベクトルポテンシャル\(\bv{A}\) が作り、ベクトルポテンシャル\(\bv{A}\) は電流密度\(\bv{ｊ}\)が作っている。

ベクトルを縦行列に表示して外積計算する
\((f_x,f_y,f_z)=(3xyz,-yz^2,x^2y)\)として

\(\color{red}{ rot\ \bv{f}= ∇ \x \bv{f} }\)
\(=\left( \begin{array}{c} \pder{}{x}\\ \pder{}{y}\\ \pder{}{z} \end{array} \right) \) \( \x \) \( \left( \begin{array}{c} f_x \\ f_y \\ f_z \end{array} \right) \) \(= \left( \begin{array}{c} \pder{f_z}{y}-\pder{f_y}{z}\\ \pder{f_x}{z}-\pder{f_z}{x}\\ \pder{f_y}{x}-\pder{f_x}{y} \end{array} \right) \)
\(= \left( \begin{array}{c} \pder{(x^2y)}{y}-\pder{(-yz^2)}{z}\\ \pder{(3xyz)}{z}-\pder{(x^2y)}{x}\\ \pder{(-yz^2)}{x}-\pder{(3xyz)}{y} \end{array} \right) \) \(= \left( \begin{array}{c} x^2+2yz\\ 3xy-2xy\\ 0-3xz \end{array} \right) \) \(\color{red}{ = \left( \begin{array}{c} x^2+2yz\\ xy\\ -3xz \end{array} \right) } \)

関係する記号の説明

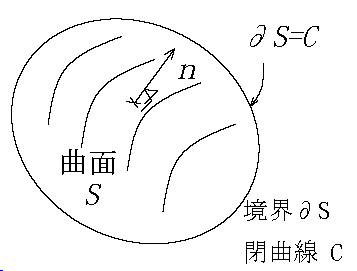
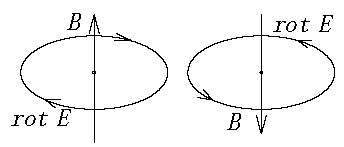
・\(\bv{E}\):電場\(\small{(N/C)}\)  ・\(V\)：電位\(\small{(V)=(J/C)}\)　　　　　
・\(\bv{B}\):磁場\(\small{(Wb/m^2)}\)（磁束密度）
・\(\Phi\):磁束\(\small{(Wb)}\)　 ・\(ds\):積分の面要素
・\(S\)：積分の閉曲面領域
・\(∂S\):積分の閉曲線(=C)  (ここでの∂記号は「境界」を表している)
・\(n\)：面要素\(dS\)の単位法線ベクトル　
・\(x\):距離　\(\small{(m)}\)
・\(\oint_{∂S}\):周回積分

ファラデーの電磁誘導の式(シンプルだが、基本となる式です)
\(V=-\der{\Phi}{t}\) \(\ :①\)

磁場(磁束密度)\( \bv{B}\) と磁束\(\Phi\)の関係式：
\(\Phi=\displaystyle \int_S \bv{B}\cdot \bv{n} ds\)\(\ :➁\)

電場(電界)\(\bv{E}\) と電位\(V\)の関係式：
\(V=\displaystyle \oint_{∂S} E \cdot d \bv{x}\) \(\ :③\)

式①に式➁、③を代入すると
\(V=\displaystyle \oint_{∂S} \color{red}{E \cdot d \bv{x}}\) \(= -\displaystyle \int_S \pder{B}{t} \cdot n dS\) \(　(=-\der{\Phi}{t})\) \(\ :④\)

ストークスの定理の式:

\( \displaystyle \int_S　\color{red}{ (∇\x \bv{E}) \cdot ndS} \) \(= \displaystyle \oint_{S} E \cdot d\bv{x} \)\(\ :⑤\)
この定理は今後の講義で扱います。

これより式④は式⑤を用いて:
\( \displaystyle \int_S ( \underline{ ∇\x \bv{E} } ) \cdot ndS \) \(= -\displaystyle \int_S \underline{\pder{B}{t} }\cdot n dS\) \(\ :④'\)

上式の下線部は等しいから
\(\therefore \ \) \(∇\x \bv{E}\) \(= \pder{B}{t}\) \(\ :❹\)