湘南理工学舎・物理数学・グリーンの定理・

グリーンの定理は二次元(平面)における定理と3次元(空間)における定理があります。
ここでは応用例が多い二次元の「平面におけるグリーンの定理」をとりあげて説明していきます。
3次元における定理はガウスの定理のあとに紹介します。

平面におけるグリーンの定理は定義式から分かるように閉曲線の周回積分の線積分と二重積分が等しいことを示しています。
線積分を思い出すと\(\cdots\) 関数f(x,y)の曲線Cに沿った積分 \(\displaystyle \int_C f(x,y) ds\) を線積分といいました。
さらにその曲線Cが図1の閉曲線のとき、 \(\displaystyle \oint_{C} f(x,y) dS\) が周回積分です。

fig1 曲線と閉曲線

上記は一般的な線積分です。
☞線積分【参照先】
本定理で扱う曲線は単一閉曲線です、これは始点と終点が同じかつ途中でそれ自身と交わらない閉曲線です。

平面におけるグリーンの定理

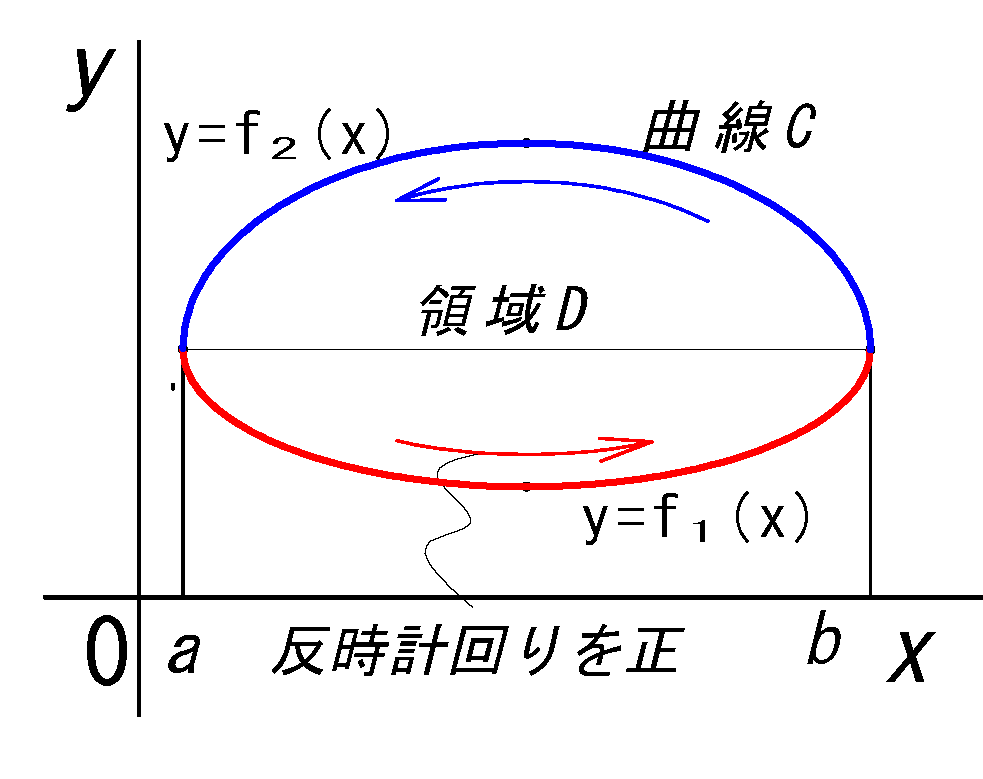
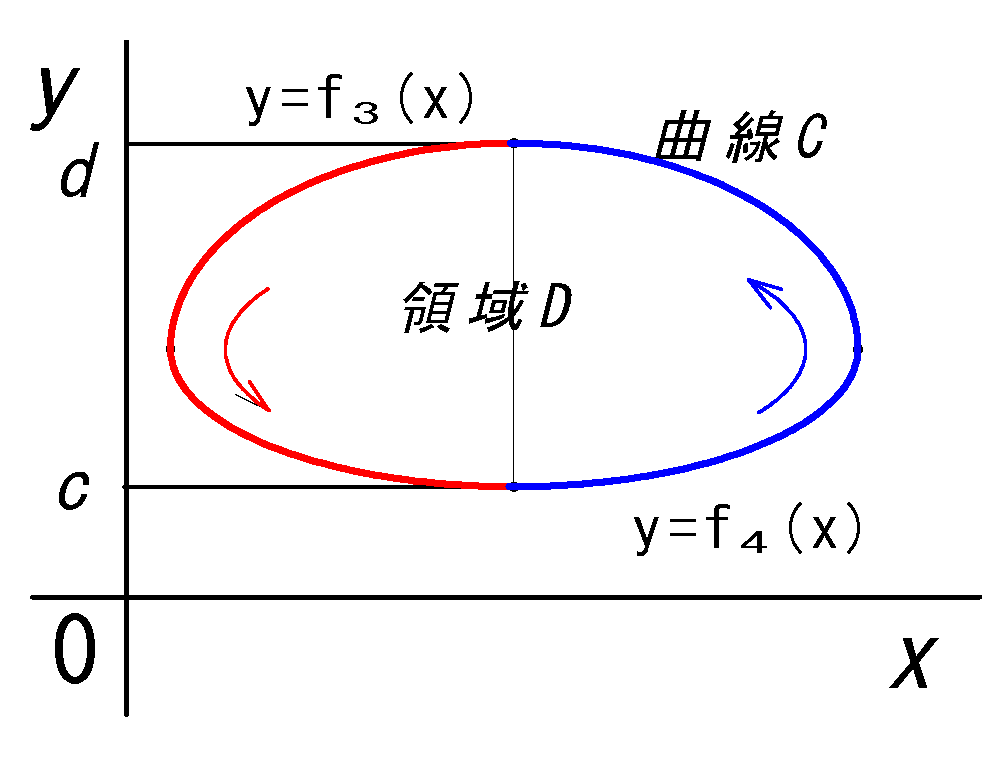
xy平面にある単一閉曲線C で囲まれた積分領域Dとして、2つ関数\(P=f_1(x,y)\)と \(Q=f_2(x,y)\)について以下の線積分と二重積分で表した下式が成り立ちます。
\(\displaystyle \oint_{C} (P(x,y)dx+Q(x,y)dy)\) \(=\dsii_{D} (\pder{Q}{x}-\pder{P}{y})dxdy \) \(\quad ❶\)

式❶の周回積分の正負は閉曲線の向きが反時計回りのとき正、時計回りのとき負です。

fig2 グリーンの定理証明1/1

fig3 グリーンの定理証明2/2

式❶の導出

\(\displaystyle \oint_{C} (P(x,y)dx+Q(x,y)dy)\) \(=\dsii_{D} (\pder{Q}{x}-\pder{P}{y})dxdy \) \(\quad ❶\)

左辺を以下のように変形していく
左辺\(=\displaystyle \oint_{C} (P(x,y)dx+Q(x,y)dy)\) \(=\underbrace{\displaystyle \oint_{C} P(x,y)dx}_{Ⓐ}+\underbrace{\displaystyle \oint_{C} Q(x,y)dy}_{Ⓑ}\)

左辺 1項はfig-2の周回積分です
\(Ⓐ=\displaystyle \oint_{C} P(x,y)dx\) \(=\underbrace{\displaystyle \int_{a}^{b} P(x,f_1(x))dx}_{曲線下側}\) \(+\underbrace{\displaystyle \int_{b}^{a} P(x,f_2(x))dx}_{曲線上側}\)
\(= \displaystyle \int_{a}^{b} P(x,f_1(x))dx\) \(-\displaystyle \int_{a}^{b} P(x,f_2(x))dx\)
\(=-\displaystyle \int_{a}^{b} \ul{\{P(x,f_2(x))-P(x,f_1(x))\} }dx\) \(=-\displaystyle \int_{a}^{b} \ul{ [P(x,y)]_{f_1}^{f_2} }\ dx\) \(=-\displaystyle \int_{a}^{b} \ul{ \int_{f_1(x)}^{f_2(x)} \dspder{P(x,y)}{y}dy }\ dx\)

\(\dsi_{f_1}^{f_2} \dspder{P(x,y)}{y}dy \) \(= \left[ P(x,y) \right]_{f_1}^{f_2}\)

\(\therefore Ⓐ=\displaystyle \oint_{C} P(x,y)dx\)\(=-\dsii_{D} \pder{P(x,y)}{y}dxdy \)

左辺 2項はfig-3の周回積分です
\(Ⓑ=\displaystyle \oint_{C} Q(x,y)dy\) \(=\underbrace{\displaystyle \int_{c}^{d} Q(f_4(y),y)dy}_{曲線右側}\) \(+\underbrace{\displaystyle \int_{d}^{c} Q(f_3(y),y)dy}_{曲線左側}\)
\(=\displaystyle \int_{c}^{d} Q(f_4(y),y)dx\) \(-\displaystyle \int_{c}^{d} Q(f_3(y),y)dy\)
\(=\displaystyle \int_{c}^{d} \ul{\{Q(f_4(y),y)-Q(f_3(y),y)\} }dy\) \(=\displaystyle \int_{c}^{d} \ul{ [Q(x,y)]_{f_3}^{f_4} }\ dy\) \(=\displaystyle \int_{c}^{d} \ul{ \int_{f_3(y)}^{f_4(y)} \dspder{Q(x,y)}{x}dx }\ dy\)
\(\therefore Ⓑ=\displaystyle \oint_{C} Q(x,y)dy\)\(=\dsii_{D} \pder{Q(x,y)}{x}dxdy \)
左辺\(＝Ⓐ+Ⓑ=\color{blue}{\dsii_{D} \pder{Q(x,y)}{x}dxdy}\)\(\color{blue}{-\dsii_{D} \pder{P(x,y)}{y}dxdy} \)

　　　
下記は❶の右辺を変形です。→ 上式の「Ⓐ+Ⓑ」と同じになりました。

右辺\(=\dsii_{D} (\pder{Q}{x}-\pder{P}{y})dxdy \) \(=\color{blue}{\dsii_{D} \pder{Q}{x}dxdy-\dsii_{D} \pder{P}{y}dxdy}\)

\(\therefore \) \(\displaystyle \oint_{C} (P(x,y)dx+Q(x,y)dy)\) \(=\dsii_{D} (\pder{Q}{x}-\pder{P}{y})dxdy \)

補足

ここで関数 P、Q は何か？→　ベクトル場P(x,y) Q(x,y)とみることができます。
あるベクトル\(F\) そのｘ成分ｙ成分を \(P(x,y), Q(x,y)\)とする。
ベクトルの線積分を思い出すと：
☞ベクトルの線積分【参照先】

\(\displaystyle \int_{c} \ \bv{F} \cdot \bv{u} ds\)　 \(=\displaystyle \int_{c} \left( F_x(x,y)dx + F_y(x,y)dy \right) \)　\(\ ❹\)

\(F_x,\ F_y\)を\(P,\ Q\) に置き換えれば次式が得られる。
\( \displaystyle \int_{c} \ \bv{F} \cdot \bv{u} dS \) \( =\displaystyle \int_{c} P(x,y)dx + Q(x,y)dy \)
さらに,曲線C が単一閉曲線なら周回積分となり、公式❶の左辺になりますね。
また、ここでは以下の例題をとおし,公式による積分計算の利便性を実感してしてください。

例題1
次の周回積分を求めよ
\(\displaystyle \oint_{C} (xy+y^2)dx+(x^2+y)dy\)
領域は\(y=x,\quad y=x^2\ \)によって囲まれた閉曲線。
解：

積分すべき領域は\(y=x,\quad y=x^2\ \)で囲まれた閉曲線だから(xy座標をイメージして):
\(x:0 \to 1 \quad y:0 \to y=x^2\)

与式より\(P(x,y)=xy+y^2,\ Q(x,y)=x^2+y\) である。
\(\dsii_{D} (\pder{Q(x,y)}{x}-\pder{P(x,y)}{y})dxdy\) \(=\dsii_{D} \{\pder{}{x}(x^2+y)-\pder{}{y}(xy+y^2)\}dxdy\)
\(=\dsii_{D} \{2x-x-2y\}dxdy\)
\(=\dsii_{D} (x-2y) \ dy\ dx\)
\( =\dsi_{x=1}^{x=0} \ul{ \dsi_{y=0}^{y=x^2} (x-2y) dy} \ dx\)

\(\ul{\dsi_{y=0}^{y=x^2} (x-2y) dy}\) \(=[xy-y^2]_{0}^{x^2}\)\(=x^3-x^4)\) \(=x^4-x^3\)

\( =\dsi_{1}^{0} (x^4-x^3) \ dx\) \( =\left[ \dsfr{1}{5}x^5 -\dsfr{1}{4}x^4 \right]_{1}^{0}\)\(=-\dsfr{1}{20}\)

例題2
次の周回積分を求めよ
\(\displaystyle \oint_{C} (x^2+ x^2y)dx+(y^2+ xy^2)dy\)
領域である曲線Ｃは半径ａの円周とする。
解：

与式より \(P=x^2+ x^2y\) \(\ \) \(Q=y^2+ xy^2\)

\( \pder{P(x,y)}{y}=\pder{}{y}(x^2+x^2y)=x^2 \)
\( \pder{Q(x,y)}{}=\pder{}{x}(y^2+xy^2)=y^2 \)
\(\dsii_{D} ( \pder{Q(x,y)}{x}-\pder{P(x,y)}{y}) dxdy\) \(=\dsii_{D} (x^2+y^2) dxdy\)

この式は極座標変換による積分計算が簡単になります。すなわち：
☞極座標変換の【参照先】
\(x=rcosθ\ y=rsinθ\) \(\ \) \(0\le r \le a\)\(\ \) \(0 \le θ \le 2\pi\)
ヤコビアン\(\color{red}{J=r}\)

　\(=\dsi_{0}^{2\pi} \dsi_{0}^{a} (r^2cos^2θ+r^2sin^2θ)\color{red}{J}\ drdθ\) \(=\dsi_{0}^{2\pi} \dsi_{0}^{a} r^2(cos^2θ+sin^2θ)\color{red}{r}\ drdθ\) 　\(=\dsi_{0}^{2\pi} \dsi_{0}^{a} r^3 \cdot 1\ drdθ\) 　\(=\dsi_{0}^{2\pi} \dsi_{0}^{a} r^3 drdθ\) 　\(=\dsi_{0}^{2\pi} \left[\dsfr{1}{4}r^4\right]_{0}^{a}\ dθ\) 　\(=\dsi_{0}^{2\pi} \dsfr{1}{4}a^4 dθ\)
　\(=\dsfr{1}{4}a^4 \left[ θ \right]_{0}^{2\pi}\) \(=\dsfr{1}{2}\pi a^4 \)
　　　

coffe

[コーヒーブレイク/閑話］…お疲れさまでした