線積分とは
場の積分にはスカラー場の線積分とベクトル場の線積分があります。 今回はスカラー場の線積分について学びます。
今までの積分はx軸に沿った積分、すなわち1変数関数なら、関数f(x)とx軸によってできる面積を求めることでした。
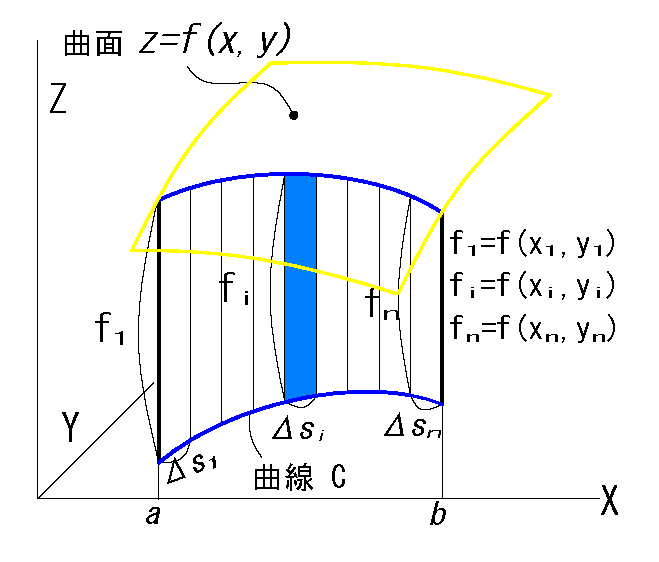
fig1 スカラー場
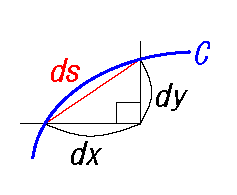
fig2 微小部拡大
線積分は曲線に沿った積分です。
ここでは2変数関数のz=f(x,y)の3次元の曲線を考えます
下図の通り、曲面z=f(x,y) をx,y 平面の
曲線 C で切った断面積が線積分です。
\(Δs\) を線素といい、\(s\)は弧長という。
切断面を曲線の沿って分割した短冊の面積の総和は:
\( \displaystyle \sum_{i=1}^n f(x_i,y_y) Δs_i \)
上式の\(n\) を大きくして、\(Δs\)→0 の極限である次の積分式を「曲線C に沿った線積分」という。
すなわち、
曲線C で切った断面積です。
\(C\):積分領域の曲線, \(f(x,y)\):短冊高さ, \(ds\):短冊幅
\(\color{red}{ \displaystyle \int_{C} \ f(x,y)\ ds }= \displaystyle \int_{a}^{b} f(x,y) ds\)
\(=\displaystyle \lim_{n \to \infty} \displaystyle \sum_{i=1}^n f(x_i,y_i) Δs_i \) \(\ ❶\) ※
※:上式の\(n\) を大きくすることは 「\(Δs\)→0」となることです。
ここで、思いだそう「曲線の長さ」
【講義名:定積分5/曲線の長さ】
【参照先】
被積分関数 \(f(x,y)=1\)(定数=1)のときの線積分の結果はどうなるだろうか…曲線の長さだと想定するでしょう。
その通りです…
\(L=\displaystyle \int_a^b \sqrt{ (\frac{dx}{dt})^2 +(\frac{dy}{dt})^2 }\ dt\)
以下に示す式❸の\(f(x(t),y(t))=1\) としたときの式と同じになる。
被積分が 【「xy平面の曲線の各点」 と 「各点の応する\(z=f(xy)=1\)」】ならその積分は「曲線の長さ」ですね。
線積分の計算1
曲線C はxy平面上にあり、\(y=g(x)\) で表すと (x,y)=(x,g(x))となる。
\(z=f(x,y)=f(x,g(x))\) ---1変数関数となる。
極めて小さい 線素 ds は直線と見なして、次のように展開できる。
\(ds=\sqrt{dx^2+dy^2}\)
\(ds= \frac{ \sqrt{dx^2+dy^2} }{dx} dx \)
\(=\sqrt{ (\frac{dx}{dx})^2 +(\frac{dy}{dx})^2 } dx \)
\(= \sqrt {1+ (\frac{dy}{dx})^2 } dx \)
これより、式❶は以下のように1変数の積分に変換できる。
\(\displaystyle \int_{C} \ f(x,y)\ ds\)
\(= \displaystyle \int_{a}^{b} f(x,g(x)) \sqrt {1+ (\frac{dy}{dx})^2 }\ dx \) \(\ ❷\)
線積分の計算2
曲線C とパラメータ(媒介変数)t を使い \((x(t),y(t))\) と表して計算する方法。
\( f(x,y)=f(x(t),y(t))\)
となり、f はt の1変数関数となり、計算が簡単になる。
(パラメータt が決まれば、x,y も決まるわけ)
\(\displaystyle \int_{C} \ f(x,y)\ ds\)\(=\displaystyle \int_{C} \ f(x(t),y(t))\ ds\)
ds を次のように展開する。
\(ds=\sqrt{dx^2+dy^2}\)
\(= \frac {\sqrt{dx^2+dy^2} } {dt} dt \)
\(=\sqrt {\frac {dx^2+dy^2}{dt^2} } dt \)
\(=\sqrt{ (\frac{dx}{dt})^2 +(\frac{dy}{dt})^2 } \ dt \)
これより、式❶は以下のように1変数t の積分に変換できる。
\(\displaystyle \int_{C} \ f(x,y)\ ds\)
\(= \displaystyle \int_{a}^{b} f(x(t),y(t)) \sqrt{ (\frac{dx}{dt})^2 +(\frac{dy}{dt})^2 } \ dt \)
\(\ ❸\)
線積分の計算の補足
上記の式❷、式❸について下式が成り立ちます。
経路が「\(C:a→b\)」の逆の「\(-C:b→a\)」 のとき:
\(\displaystyle \int_{-C} \ f(x,y)\ ds\)
\(=-\displaystyle \int_{C} \ f(x,y)\ ds\) \(\ ❹\)
経路\(C\) の分割(\(C=C_1+C_2+\cdots+C_n\))のとき:
\(\displaystyle \int_{C} \ f(x,y)\ ds\)
\(=\displaystyle \int_{C_1} \ f(x,y)\ ds\)
\(+\displaystyle \int_{C_2} \ f(x,y)\ ds\)
\(+\cdots\)
\(+\displaystyle \int_{C_n} \ f(x,y)\ ds\)\(\ ❹\)
例題1
スカラー場\(f(xy)\) の曲線C 沿っての線積分を求めよ。
\(f(x,y)=2x+y\) \(\quad \) \(C:y=2x\) \(\ (0\le x \le 4)\)
式❷を使い求める。
\(\int_{a}^{b} f(x,g(x)) \sqrt {1+ (\frac{dy}{dx})^2 }\ dx \) \(\ ❷\)
\(y=g(x)=2x\)
\(f(x,y)=f(x,g(x))=2x+2x=4x\)
\(\der{y}{x}=(2x)'=2\)
これらを式❷に代入する。
\(\displaystyle \int_{C} \ (2x+y)\ ds\)
\(= \displaystyle \int_{0}^{4} 4x \sqrt {1+ (2)^2 }\ dx \)
\(=4\sqrt{5} \ \left[ \frac{1}{2}\ x^2 \right]_0^4\)\(= 32 \sqrt{5}\)
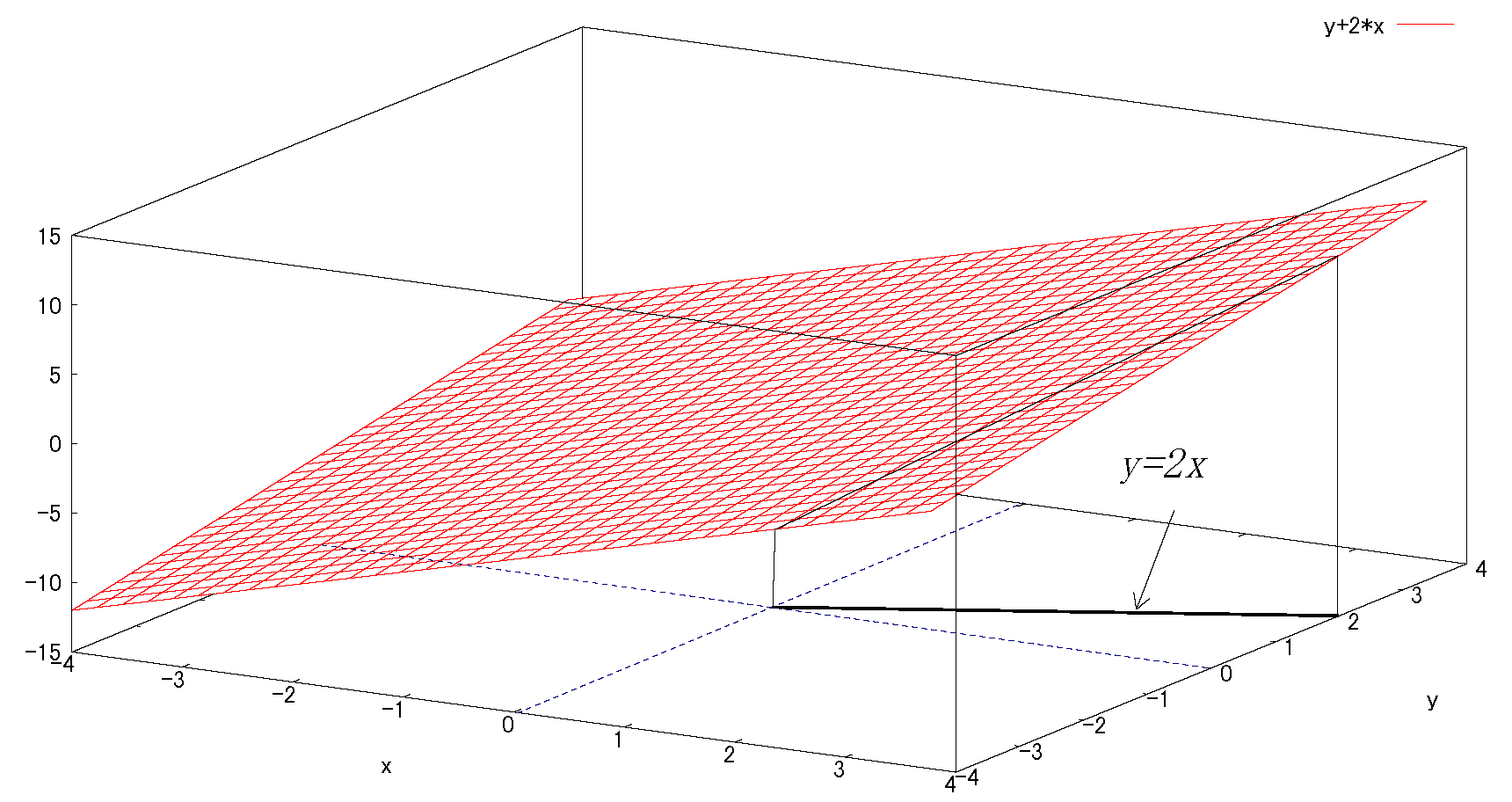
fig3 \(f(x,y)=2x+y\)
例題1と同じスカラー場、曲線において 媒介変数t による線積分を求めよ。
\(f(x,y)=2x+y\) \(\quad \) \(C:y=2x\) \(\ (0\le x \le 4)\) に対し
式❸を使い求める。
\(\int_{a}^{b} f(x(t),y(t)) \sqrt{ (\frac{dx}{dt})^2 +(\frac{dy}{dt})^2 } \ dt \)
\(\ ❸\)
\(x=t\) とすると\(y=2t\) \(\ (0\le t \le 4)\) である。
\(\der{x}{t}=(t)'=1\) \(\ \) \(\der{y}{t}=(2t)'=2\)
これらを式❸に代入する。
\(\displaystyle \int_{C} \ (2x+y)\ ds\)
\(=\displaystyle \int_{0}^{4} (2t+2t) \sqrt {1^2+ (2)^2 }\ dt \)
\(=\displaystyle \int_{0}^{4} (4t) \sqrt {5}\ dt \)
\(=4\sqrt{5} \ \left[ \frac{1}{2}\ t^2 \right]_0^4\) \(= 32 \sqrt{5}\)
例題3
スカラー場\(f(xy)\) の曲線C 沿っての線積分を求めよ。
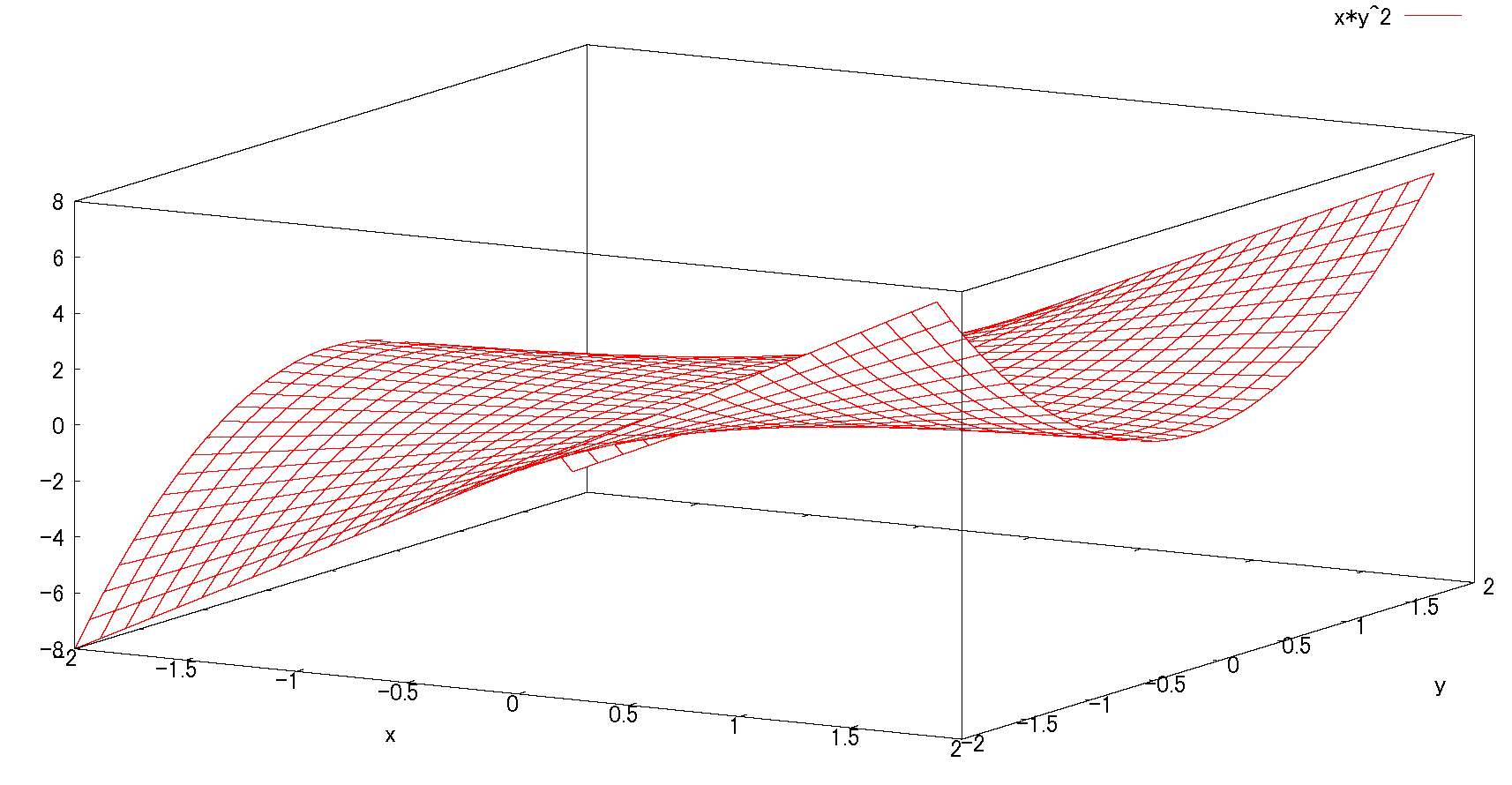
\(f(x,y)=xy^2\) \(\quad \) \(C=(t,2-t)\) \(\ (0\le t \le 2)\)
\( (t,2-t)=(x,y) \)とする
式❸を使い求める。
積分経路の明記がないから\(x=t,\ y=2-t\)として\((0,2)-(2,0)\)を結ぶ直線である。
すなわち\(y=-x+2 \)の経路である。
\(\der{x}{t}=(t)'=1\) \(\ \) \(\der{y}{t}=(2-t)'=-1\)
これらを式❸に代入する。
\(\displaystyle \int_{C} \ xy^2\ ds\)
\(=\displaystyle \int_{0}^{2} t(2-t)^2 \sqrt {1^2+ (-1)^2 }\ dt \)
\(=\displaystyle \int_{0}^{2} t(2^2-4t+t^2) \sqrt {2}\ dt \)
\(=\sqrt {2} \displaystyle \int_{0}^{2} (4t-4t^2+t^3) \ dt \)
\(=\sqrt {2} \left[\frac{4}{2}t^2-\frac{4}{3}t^3+\frac{1}{4}t^4 \right]_0^2\)
\(=\sqrt{2} \ \left[8-\frac{32}{3}+4 \right]\)
\(=\sqrt{2} \frac{36-32}{3} \)
\(=\sqrt{2}\ \frac{4}{3}\)
例題4
例題3と同じスカラー場、積分経路において 式❷ により線積分を求めよ。
\(f(x,y)=xy^2\) \(\quad \) \(C=(t,2-t)\) \(\ (0\le t \le 2)\)
例題3の積分経路の\((x,y)\)表示の点は:
\(t=0 :(0,2) \quad t=2 :(2,0) \) だから
\(y=g(x)=-x+2\) となる。
これより
\(f(x,y)=f(x,g(x))\) \(=xy^2=x(-x+2)^2\)\(=x^3-4x^2+4x\)
\(\der{y}{x}=(-x+2)'=-1\)
これらを式❷ に代入する
\(\displaystyle \int_{C} \ xy^2\ ds\)
\(= \displaystyle \int_{0}^{2} (x^3-4x^2+4x) \sqrt {1+ (-1)^2 }\ dx \)
\(=\sqrt{2} \displaystyle \int_{0}^{2} (x^3-4x^2+4x)dx\)
\(=\sqrt{2} \ \left[ \frac{1}{4}\ x^4-\frac{4}{3}\ x^3 + \frac{4}{2}\ x^2 \right]_0^4\)
\(=\sqrt{2} \ \left( \frac{16}{4}-\frac{32}{3} + \frac{16}{2}\right) \)
\(=\sqrt{2} \ \left( 4+8 -\frac{32}{3} \right) \)
\(= \sqrt{2}\ \frac{4}{3}\)
勿論、答は例題3 と同じになりました。