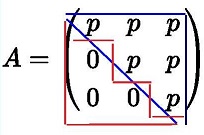
階段行列でない例:
\(\begin{pmatrix} 1 & 2 & 1 \\
1 & 2 & 2 \\
0 & 0 & 0
\end{pmatrix}
\quad
\begin{pmatrix} 0 & 5 & 3 \\
3 & 1 & 2 \\
0 & 0 & 1
\end{pmatrix} \)
\( \begin{pmatrix} 1 & 2 & 1 \\
0 & 0 & 2 \\
0 & 1 & 2
\end{pmatrix}\)
上の3つの行列は下に向かい、左からゼロが増えてる形でない。
しかし3番目の行列は2行と3行を入れ替えれば階段行列となる。
\( \begin{pmatrix} 1 & 2 & 1 \\
0 & 1 & 2 \\
0 & 0 & 2
\end{pmatrix} \)
階数: \(rank(A)=3 \)
2.行基本変形の例
(row basic transformation)
階段行列に変形して階数を求めてみます。
注:「②-①」とは「②行目から①行目を減算」を意味します。
②-①、③-① → ②と③の入れ替え
\(\begin{pmatrix} 1 & 2 & 1 \\
1 & 2 & 2 \\
1 & 3 & 3
\end{pmatrix}
\begin{array}{c}
①\\
②\\
③
\end{array}
\rightarrow
\begin{pmatrix} 1 & 2 & 1 \\
0 & 0 & 1 \\
0 & 1 & 2
\end{pmatrix} \)
\( \quad \rightarrow
\begin{pmatrix} 1 & 2 & 1 \\
0 & 1 & 2 \\
0 & 0 & 1
\end{pmatrix} \)
この行列は単位行列にできるが、階数を求めるだけならここで終わる。
3.拡大係数行列における階数
(rank of expantion coefficient matrix)
(連立方程式の解の種類)
はじめに、記載する行列の書式を説明します。
\( a_{i1} x_1 + a_{i2} x_2 + a_{i3} x_3= b_i\)
の連立方程式の行列を以下のように表します。
\(
\left( \begin{array}{ccc|c}
x_1 & x_2 & x_3 & b_i\\
\hline
a_{11} & a_{12} & a_{13}& b_1\\
a_{21} & a_{22} & a_{23}& b_2\\
a_{31} & a_{32} & a_{33}& b_3\end{array}
\right)
\)
これから連立方程式の
階数から方程式の自由度、解の存在について述べていきます。
•拡大係数行列\(V\ \)は係数行列\(A\ \)と定数項の\(b\ \)から構成されている。
•方程式は\(Ax=b \)
•拡大係数行列\( V(A|b)\),そのランクは\(rank(A,b)\)と表す。
•未知数 \(n=3 \ (x_1,x_2,x_3)\) とします。
ここで一例をあげます
③+②x4 ➝
\(
\left( \begin{array}{cccc}
1 & 1 & 1 & 0\\
0 & -1 & 1 & 0\\
0 & 4 & -5 & -3\end{array}
\right)
\)
\(
=\left( \begin{array}{cccc}
1 & 1 & 1 & 0\\
0 & -1 & 1 & 0\\
0 & 0 & -1 & 1\end{array}
\right)
\)
これより 階数
\(rank(A)=rank(A,b)=3\) が求まりました。
この行列はさらに行変形ができ、次のように単位行列にもちこめる。
(行変形の過程は割愛します)
\(
\left( \begin{array}{cccc}
1 & 0 & 0 & 3\\
0 & 1 & 0 & -2\\
0 & 0 & 1 & -1\end{array}
\right)
\)
\(
\begin{array}{c}
x_1=3\\
x_2=-2\\
x_3=-1\end{array}
\)
未知数の\(x_1,x_2,x_3\) が直接求められました。
以下は3つの代表的な例です。
【例1】解は一意
\(
\left( \begin{array}{cccc}
1&2&1&2\\
0&1&2&2\\
0&0&1&1\end{array}
\right)
\)
\(rank(A)=rank(A,b)=3\)
行列Vの階数と行列Aの階数が等しい。
自由度\(=n-3=0 \)
方程式の
解は一意。
(解の未知数\(x_1,x_2,x_3 \)はただ一つ)
注:これと同値は
係数行列があとで学ぶ
正則なことです。
すなわち行列式|A|が「0」でないことです。
【例2】解は無数
\(
\left( \begin{array}{cccc}
1&1&-1&3\\
0&-1&5&0\\
0&0&0&0\end{array}
\right)
\)
\(rank(A)=rank(A,b)=2\)
自由度\(=n-2=1 \)
この
解は無数ある。
…なぜ?【参考先】
【例3-1】解は存在しない
\(
\left( \begin{array}{cccc}
1&0&-1&1\\
0&1&2&2\\
0&0&0&1\end{array}
\right)
\)
\(rank(A)=2, rank(A,b)=3\)
\(rank(A)<rank(A,b)\)
この
解は存在しない。
…なぜ?【参考先】
【例3-2】解は存在しない
\(
\left( \begin{array}{cccc}
2& -1& 2& -1\\
0& 0& 0& 7\\
0& 0& 0& 0\end{array}
\right)
\)
\(rank(A)=1, rank(A,b)=2\)
\(rank(A)<rank(A,b)\)
この
解は存在しない。
4.拡大係数行列の一般化
(generalization of expantion coeffient matrix)
今までのことを一般的な拡大係数行列\(V\ \)に表記に展開します。
まず、次の拡大係数行列を考えます。
\(V=\left( \begin{array}{rr|rr}
1&0&-1&2\\
0&1&2&3\\
\hline
-2&3&4&4\end{array}
\right)
\)
この拡大係数行列の係数行列
(\(rank(A)=2\))
は単位行列ではないが、左上部は(2x2)型行列の単位行列です。
このように行基本変形により単位行列を左上に配置したきれいな型に変形します。
階数を求める操作には係数行列部の列の交換(※)をしてもよい。
注(※):前回学んだ
列基本変形の中の操作
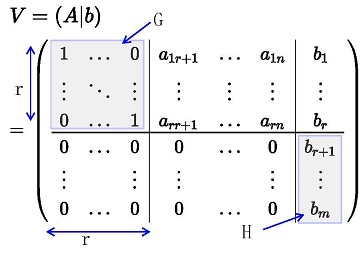
これを一般的な拡大係数行列\(V\ \)で表記してみます。
A(m行,n列)、b(m行,1列) V(m行,n+1列)
この行列の持つ意味について解説していきます。
拡大係数行列\( V(A|b)\),
そのランクは\(rank(A,b)\)と表す。
•この図のAの行列:
rank(A)=r (最大はm )
•階数の範囲:
\( m≥rank(A,b)≥rank(A)\)
•解を持つ条件:
\(rank(A,b)=rank(A)=r \)
(H部の\( b_{r+1} \dots b_m \)が全て0の時)
•H部が0でない時:
\(rank(A,b)>rank(A)\)であり、解はもたない。
•解の自由度:\(n-r\)
•解が一意の条件:
(解がただ1つ)
\(rank(A)=r=n \)
上記と重複するが;
H部が全部ゼロなら方程式は解を持つ。
\(rank(A,b)=rank(A)=r \)
\( b_{r+1}, \dots ,b_m=0\)
H部にゼロ以外が1つでもあれば方程式は解を持たない。
\(rank(A,b)>rank(A)\)
5.正則行列
(regular matrix)
正則行列は線形代数において次のような重要な性質をもちます。
正方行列である
n 次正則行列Aにおいて:
•行列式\( |A| =det|A|\neq 0 \)
•\(rank (A)=n\) ⇒ただ1組の解をもつ。
•Iを単位行列として、
\( XA=AX=I \)
となるXが存在するとき、行列Aは正則行列である。
このときのXをAの
逆行列という。
\(A^{-1}\)と表す。
以下は逆行列の性質です。
①\(A^{-1} A=A A^{-1}=I \)
②行列\(A\) の逆行列はただ1つ存在する。
逆行列は証明や式の変形などに、よく多用される。
•AとBが同次の正則行列のとき、その積 AB も正則行列であり、その逆行列は次式となる。
\( (AB)^{-1}=B^{-1}A^{-1}\)
[証明】:
\((AB)\)
の左から\(B^{-1}A^{-1}\)をかける。
\(\color{red}{(B^{-1}A^{-1})} \color{blue}{(AB)} =B^{-1}(A^{-1}A) B\)
\(=B^{-1}I B=B^{-1} B=I \)
同様に
\((B^{-1}A^{-1})\)
の左から\((AB)\)をかける。
\(\color{blue}{(AB)}\)\(\color{red}{(B^{-1}A^{-1})} \)=\(A (B B^{-1}) A^{-1} \)
\(=A I A^{-1}\)\(=A A^{-1}=I \)
すなわち
\((AB)\)
の逆行列が存在し、
\( (AB)^{-1}=B^{-1}A^{-1}\)
です。
6.逆行列の求め方
(how to find inverse matrix)
逆行列の求め方は掃き出し法と余因子による方法があります。ここでは掃き出し法による方法で逆行列を求めます。
余因子による方法は後の講義で行います。
正則な正方行列Aに対して行基本変形を何回か行い、右辺にできる行列は単位行列になります。
左側が行列\(A\)、右側に単位行列\(I\)を並べる。
そして
左側の行列\(A\)に行基本変形をして単位行列にすると、右側が求める逆行列\(A^{-1}\)になる。
【例題1】
次の(2x2)型行列の逆行列を求める
\(A=
\begin{pmatrix} 6 & 2 \\
3 & 2
\end{pmatrix} \)
【例題2】
次の(3x3)型行列の逆行列を求める
\(A=
\begin{pmatrix} 1 & 2 & -1 \\
1 & -1 & 1 \\
0 & -2 & 1
\end{pmatrix} \)