関数 f(x) の x軸上の点 a の近傍における近似式を与えるのがテイラー展開、また原点 (x=0) 近傍における近似式を与えるのがマクローリン展開です。
テイラーの定理でm 個の有限個のべき級数(整級数)、すなわち有限級数で表現されいる。
テイラー展開は無限級数で表現され、テイラー級数とも呼ばれている。
|
1変数のテイラーの定理
f(x) は開区間 I=(a,b) において \(n\) 回微分可能(\(C^{n}\)級 )のとき、
下式が成り立つ。
テイラーの定理の式は多項式を有限個にとめて最後の項に剰余項をつけている。 \(f(x)=\color{blue}{f(a)+\frac{f'(a)}{1!}(x-a)+\frac{f''(a)}{2!}(x-a)^2+}\) \(\color{blue}{\cdots+\frac{f^{(n-1)}(a)}{(n-1)!}(x-a)^{(n-1)}}\)\(+\frac{f^{n}(c)}{n!}(x-a)^n \) :❶ \(f(x)=\color{blue}{ \displaystyle \sum_{m=0}^{n-1} \frac{f^{m}(a)}{m!}(x-a)^m}\)\(+\frac{f^{n}(c)}{n!}(x-a)^n\) :❶' 最終項の剰余項だけ f(a) でなく f(c) であり、またこの項を\(R_n\)とおくと。 \(R_n=\frac{f^{n}(c)}{n!}(x-a)^n\) :❷ \(R_n\)のことをラグランジュの剰余項(または誤差項)と呼んでいる。
\(c\) は
\(c=a+θ(x-a)\)
であり、θは小さな値として\(0\ltθ\lt1\)と定義されている。 n が無限大、剰余項が 0 に収束するとき下式が成り立つ: \(f(x)=\color{blue}{ \displaystyle \sum_{m=0}^{n-1} \frac{f^{m}(a)}{m!}(x-a)^m}\) 注:以下のように、式❶の x を b にした式もある。
開区間 (a,b)においてn回微分可能として |
関数\(z(t)\)は\(C^{n}\)級(※)とする。
\(z(t)=f (\ x(t),y(t)\ )=f\ (a+ht,b+kt) \)
\(x(t)=a+ht\) \( \ ,\ \) \(y(t)=b+kt\)
全微分可能ならば連鎖律【参照先】が使える。
偏導関数が存在し、その偏導関数が連続なら全微分可能(※)である。
上記の「\(z(t)\)は\(C^{n}\)級(※)」がこれを満足している。
\(\dera{z}{t}=\pder{z}{x}\dera{x}{t}+\pder{z}{y}\dera{y}{t}\)
\(=\pder{z}{x}h+\pder{z}{y}k\)
(\(\dera{x}{t}=h\) \( \ ,\) \(\frac{dy}{dt}=k\))
\(=(h\pder{}{x}+k\pder{}{y})z\)
\(\dera{z}{t}=\dera{f}{t}=\color{red}{(h\pder{}{x}+k\pder{}{y})} \ f\)
\(\pder{f}{x}=\color{red}{\pder{}{x}}\ f\)
\(\color{red}{\pder{}{x}}\)
を微分作用素という。 \(\color{red}{\pder{}{x}}\)は\(f\)に(微分操作)を作用している。
\(\color{red}{(h\pder{}{x}+k\pder{}{y})}\)も微分作用素といえる。
|
2変数関数のテイラーの定理
\(z=f(x,y)\)は開領域 \(D\) において\(C^{n}\)級とする。
\( (a,b) \in D\) \(\quad \) \( h,k \in \bv{R}\) ((a,b)は開領域 \(D\) 内で定義され、\( h,k \)は実数である。)
線分 \((a,b)-(a+h,b+k)\)は領域 \(D\)に含まれる。 \(R_n= \frac{1}{n!} (h\pder{}{x}+ k \pder{}{y})^n\) \( \ f(a+\theta h, b+\theta k)\) :② |
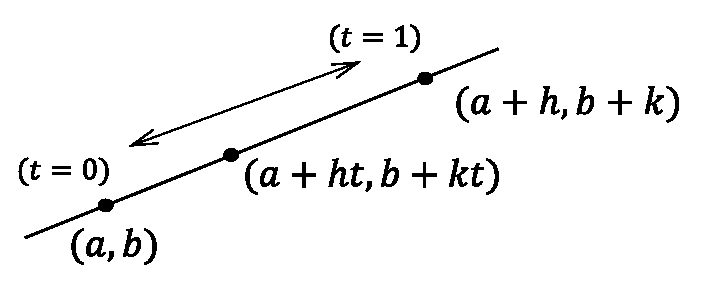
\(x(t)=a+ht\) \( \ ,\) \(y(t)=b+kt\)
\(F(t)=f (\ x(t),y(t)\ )\) \(=f(a+ht,b+kt)\)
\(F(\theta)=f (\ x(\theta),y(\theta)\ )\) \(=f(a+h\theta ,b+k\theta )\)
\(F^{(1)}(t)=f'=\dera{f}{t}\) \(=\pder{f}{x}\dera{(ht)}{t} + \pder{f}{y}\dera{(kt)}{t}\) \(=\pder{f}{x}h + \pder{f}{y}k\) \(=(h \pder{}{x} + k \pder{}{y})\ f \)
\(F^{(2)}(t)=\dera{}{t}\dera{f}{t} \)\(=\color{red}{\dera{}{t}}[(h\pder{}{x} + k\pder{}{y})\ \color{red}{f}\ ] \)
\(=\color{red}{\dera{f}{t}}\ (h\pder{}{x} + k\pder{}{y}\ ) \)
\(=\color{red}{(h\pder{}{x} + k\pder{}{y}\ )f } \ (h\pder{}{x} + k\pder{}{y}\ ) \)
\(\quad =(h\pder{}{x} + k\pder{}{y})^2 \ f \)
同様にして
\(\quad \quad \quad \vdots\)
\(F^{(m)}(t)= (h\pder{}{x} + k\pder{}{y})^m\)\( \ f(a+ht,b+kt) \) \(:(ⅰ)\)
\(f(x)=\displaystyle \sum_{m=0}^{n-1} \frac{f^{m}(a)}{m!}(x-a)^m\)\(+\frac{f^{n}(c)}{n!}(x-a)^n\)
:❶'
最終項の剰余項を\(R_n\)とおく。
\(R_n=\frac{f^{n}(a+θ(x-a))}{n!}(x-a)^n\) :❷'
式❶'に対して
\(t\) は \(0→1\) を動くから (x-a) に (1-0) を代入、t=1 だから x に 1 を代入すると:
(\((1-0)→(x-a),\ 1(=t)→x \ \))
\(f(1)=\displaystyle \sum_{m=0}^{n-1} \frac{f^{m}(0)}{m!}(1-0)^m\)\(+\frac{f^{n}(c)}{n!}(1-0)^n\)
\(f(1)=\displaystyle \sum_{m=0}^{n-1} \frac{f^{m}(0)}{m!}\)\(+\frac{f^{n}(c)}{n!}\)
\(:(ⅱ)\)
となる。
\(\color{blue}{F(1)}=f(a+h,b+k)\) \(=\displaystyle \sum_{m=0}^{n-1} \frac{ F^{(m)}(0) } {m!} (1-0)^n\)\(+R_n\) \(=\displaystyle \sum_{m=0}^{n-1} \frac{ F^{(m)}(0) } {m!}\) \(+\color{red}{R_n}\)
上記の剰余項 \(R_n\)は:
\(\color{blue}{F(1)}=\displaystyle \sum_{m=0}^{n-1} \frac {F^{(m)}(0)}{m\ !}\) \(+ \frac { F^{(n)} }{n\ !}(\theta)\)
\(:(ⅲ)\)
\(F(1)=f(a+h,b+k)\)
\(F(0)=f(a,b)\)
\(F^{(m)}(0)=(h\pder{}{x} + k\pder{}{y})^m \ f(a,b)\)
\(R_n=F^{(n)}(\theta)\)\(=(h\pder{}{x} + k\pder{}{y})^n\ f(a+h\theta , b+k \theta)\)
\(f(a+h,b+k)\)\(=\displaystyle \sum_{m=0}^{n-1} \frac{1}{m!} (h\pder{}{x} + k\pder{}{y})^m f(a,b)\)\( +R_n\)
\(R_n=\frac{F^{(n)}(\theta)}{n!}\)\(=\frac{1}{n!}(h\pder{}{x} + k\pder{}{y})^n\ f(a+h\theta , b+k \theta)\)
|
2変数関数のマクローリンの定理
\(f(x,y)=\displaystyle \sum_{m=0}^{n-1} \frac{1}{m!}
(\ h\pder{}{x}+ k \pder{}{y}\ )^{\ m} \ f\ (0,0)\) \(+R_n \) :③
\(R_n= \frac{1}{n!} (h\pder{}{x}+ k \pder{}{y})^n\) \( \ f(\theta x, \theta y)\) :④ 注:上式の\(h,k\) を\(x,y\) に表記した式もある。 \( \quad(\because x=a+ht,\ a=0,\ t=1 \rightarrow x=h) \) |
\((x+h,y+k)\)\(\rightarrow\)\((x,y)\), \(R_n\)項の \(h,k\)\(\rightarrow\)\(x,y\)
\(h \rightarrow\ x-a\) \(,\) \(k\ \rightarrow\ x-b\)
(\(\because\ t=1\)として \(x=a+h\) \(,\) \(y=b+k\))
|
2変数関数のテイラー展開
\(f(x,y)=\displaystyle \sum_{m=0}^{n-1} \frac{1}{m!}
(\ (x-a)\pder{}{x}+ (y-b) \pder{}{y}\ )^{\ m} \ f\ (a,b)\) \(+R_n \) :⑤
\(R_n= \frac{1}{n!} (h\pder{}{x}+ k \pder{}{y})^n\) \( \ f(\theta x, \theta y)\) :⑥ テイラー級数 \( \displaystyle \lim_{ n \to \infty } R_n(x) = 0 \) のときテイラー展開は級数(無限)となる。 \(f(x,y)=\displaystyle \sum_{m=0}^{\infty} \frac{1}{m!} (\ (x-a)\pder{}{x}+ (y-b) \pder{}{y}\ )^{\ m} \ f\ (a,b)\) :⑦ |
|
2変数関数のマクローリン展開
\(f(x,y)=\displaystyle \sum_{m=0}^{n-1} \frac{1}{m!}
(\ x\pder{}{x}+ y \pder{}{y}\ )^{\ m} \ f\ (0,0)\) \(+R_n \) :⑧
\(R_n= \frac{1}{n!} (h\pder{}{x}+ k \pder{}{y})^n\) \( \ f(\theta x, \theta y)\) :⑨ マクローリン級数 \( \displaystyle \lim_{ n \to \infty } R_n(x) = 0 \) のときマクローリン展開は級数(無限)となる。 \(f(x,y)=\displaystyle \sum_{m=0}^{\infty} \frac{1}{m!} (\ x\pder{}{x}+ y \pder{}{y}\ )^{\ m} \ f\ (0,0)\) :⑩ |
・\(h=x-a\)\(\ ,\ \) \(k=y-b\)とする。
・また展開途中に\(f(a,b)\) の\((a,b)\) を省略している。
\(\frac{1}{1!}(h\pder{}{x}+k \pder{}{y})^{1} f(a,b)\)
\(=1\cdot(h\pder{}{x}+k \pder{}{y})\cdot f\)
\(=1\cdot(h\pder{f}{x}+k \pder{f}{y})\)
\(=hf_x(a,b)+kf_y(a,b)\)
\(\frac{1}{2!}(h\pder{}{x}+k \pder{}{y})^{2} f(a,b)\)
\(=\frac{1}{2}(h^2 \pdera{f}{x}+2hk\frac{\partial^2 f}{\partial y \partial x}+k^2\pdera{f}{y})\)
\(=\frac{1}{2}(h^2 f_{xx}(a,b) +2hkf_{xy}(a,b)+k^2f_{yy}(a,b))\)
(注:\(f_{yx}=f_{xy}\) を用いた)
\(\frac{1}{3!}(h\pder{}{x}+k \pder{}{y})^{3} f(a,b)\)
\(=\frac{1}{6} (h^2 f_{xx}+2hkf_{xy}+k^2f_{yy})(h\pder{}{x}+k \pder{}{y})\)
\(=\frac{1}{6} (h^3f_{xxx}+3h^2kf_{xxy}+3hk^2f_{xyy}+k^3f_{yyy})\)
\(\frac{1}{4!}(h\pder{}{x}+k \pder{}{y})^{4} f(a,b)\)
\(=\frac{1}{4!}(h^3f_{xxx}+3h^2kf_{xxy}+3hk^2f_{xyy}+k^3f_{yyy})\)\((h\pder{}{x}+k \pder{}{y})\)
\(=\frac{1}{24} [h^4f_{xxxx}(0,0)\) \(+4h^3k f_{xxxy}(0,0)+6h^2 k^2f_{xxyy}(0,0)\)\(+4hk^3f_{yyyx}(0,0)+k^4f_{yyyy}(0,0)]\)
上記は次の微分順序交換(シュワルツの定理)を使っている。【参照先】
\(f_{xxy}=f_{xyx}=f_{yxx}\)
\(f_{yyx}=f_{yxy}=f_{xyy}\)
\(f(x,y)=f(a,b)+hf_x(a,b)+kf_y(a,b)\)
\(h\)と\(k\)を元に戻し書き直すと
これは点(a,b) での接平面の方程式である。【参照先】
冒頭の2変数関数のテイラー展開の1次近似は接平面であることが確認できた。
\(f_x(2,1)=2x=4\) \(,\ \) \(f_y(2,1)=-4y=-4\)
\(f_{xx}(2,1)=2\) \(,\ \) \(f_{yy}(2,1)=-4\)
\(f_{xy}=f_{yx}=0\)
\(f(x,y)=\displaystyle \sum_{m=0}^{n-1} \frac{1}{m!} ( (x-a)\pder{}{x}+ (y-b) \pder{}{y} )^{m}\)\(f (a,b)\)
\(f(x,y)=\underbrace{f(a,b)}_{m=0}\)\(+\underbrace{hf_x(a,b)+kf_y(a,b)}_{m=1}\)
\(+\underbrace{\frac{1}{2}(h^2 f_{xx}(a,b) +2hkf_{xy}(a,b)+k^2f_{yy}(a,b))}_{m=2}\)
\(=f(2,1)\)\(+[hf_x(2,1)+kf_y(2,1)]\)
\(+[\frac{1}{2}(h^2 f_{xx}(2,1) +2hk\underbrace{f_{xy}(2,1)}_{0}+h^2 f_{yy}(2,1))]\)
\(=f(2,1)\)\(+ [(x-2)f_x(2,1)+(y-1)f_y(2,1)] \)
\(+[\frac{1}{2}((x-2)^2 f_{xx}(2,1) + (y-1)^2 f_{yy}(2,1)) ]\)
\( =2+[(4(x-2)-4(y-1)]\) \( + [\frac{1}{2}( 2(x^2-2x+4)-4(y^2-2y+1) )]\)
\( =\underline{2+[(4x-4y-4]}\) \( + \frac{1}{2}[( 4x^2-4x-8)-4y^2+8y+4]\)
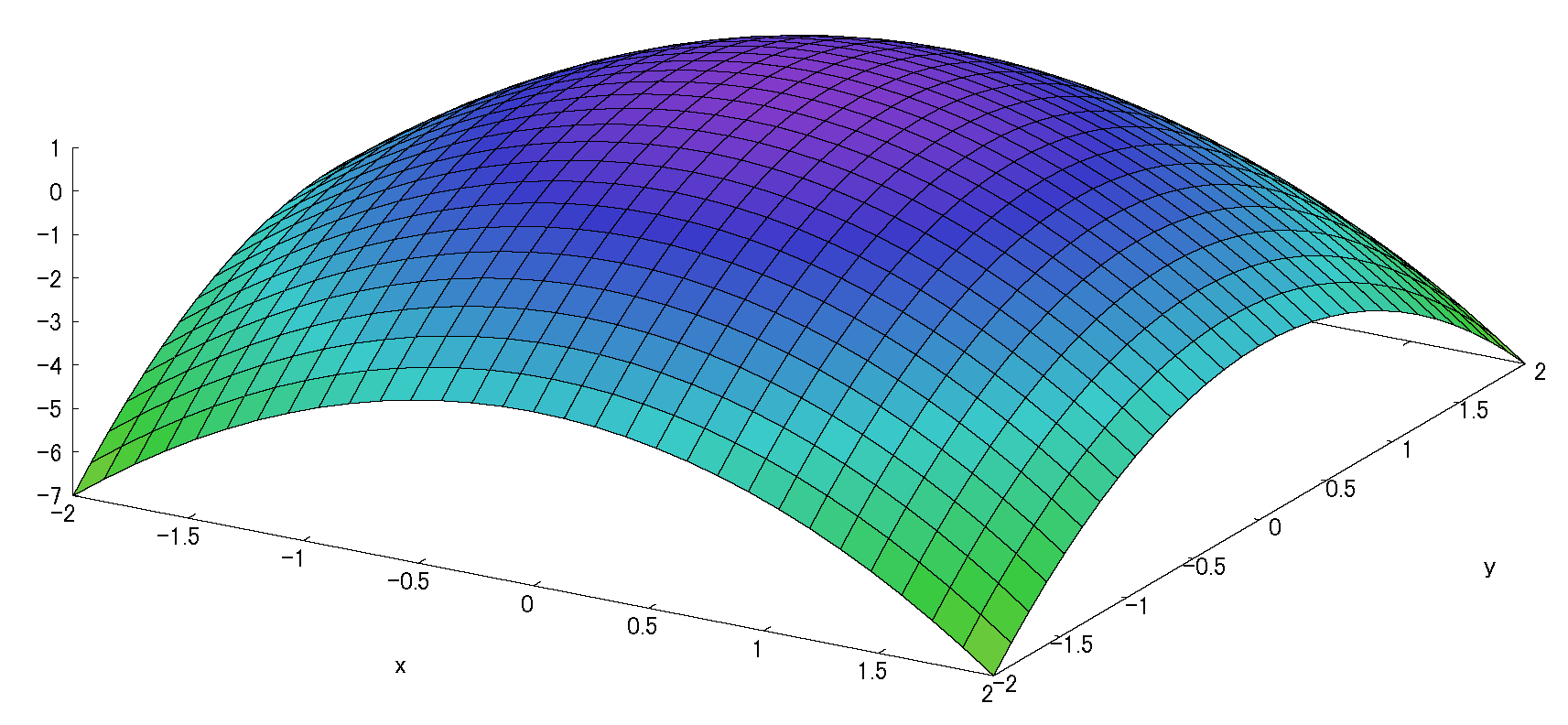
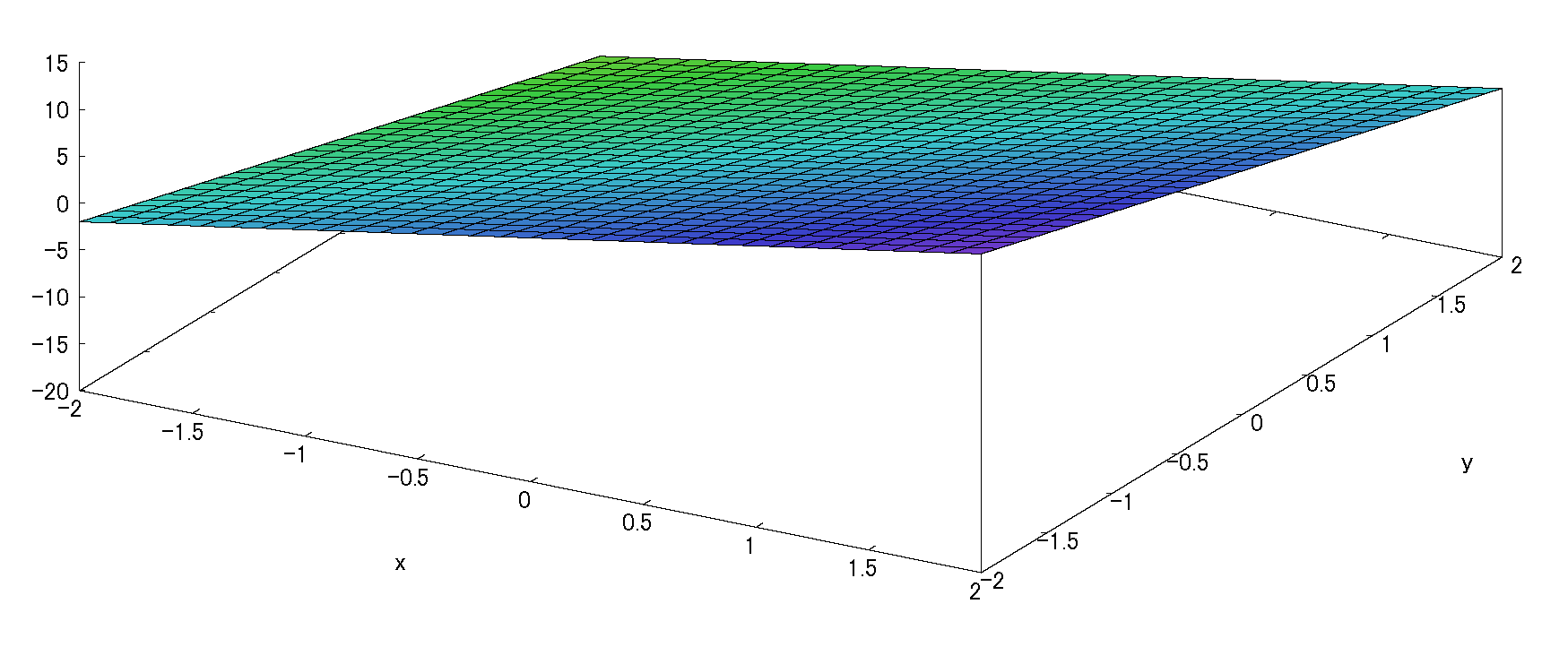
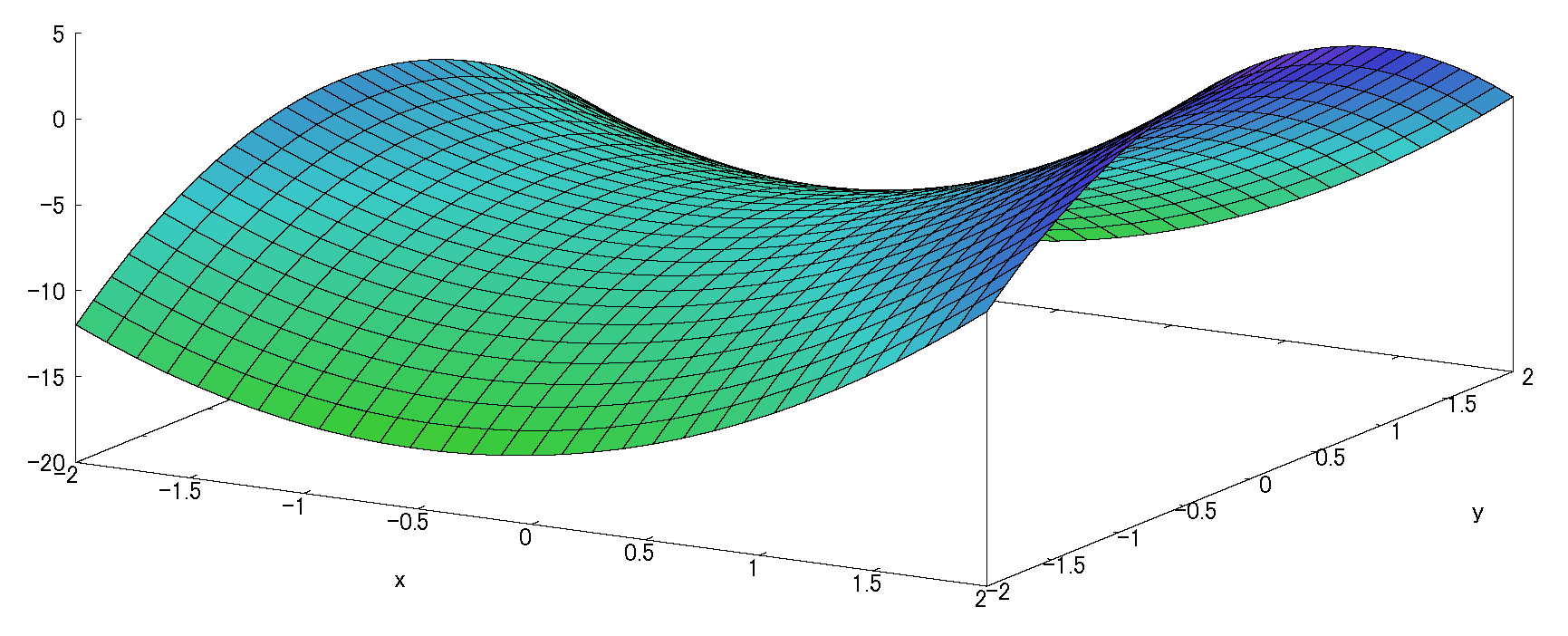
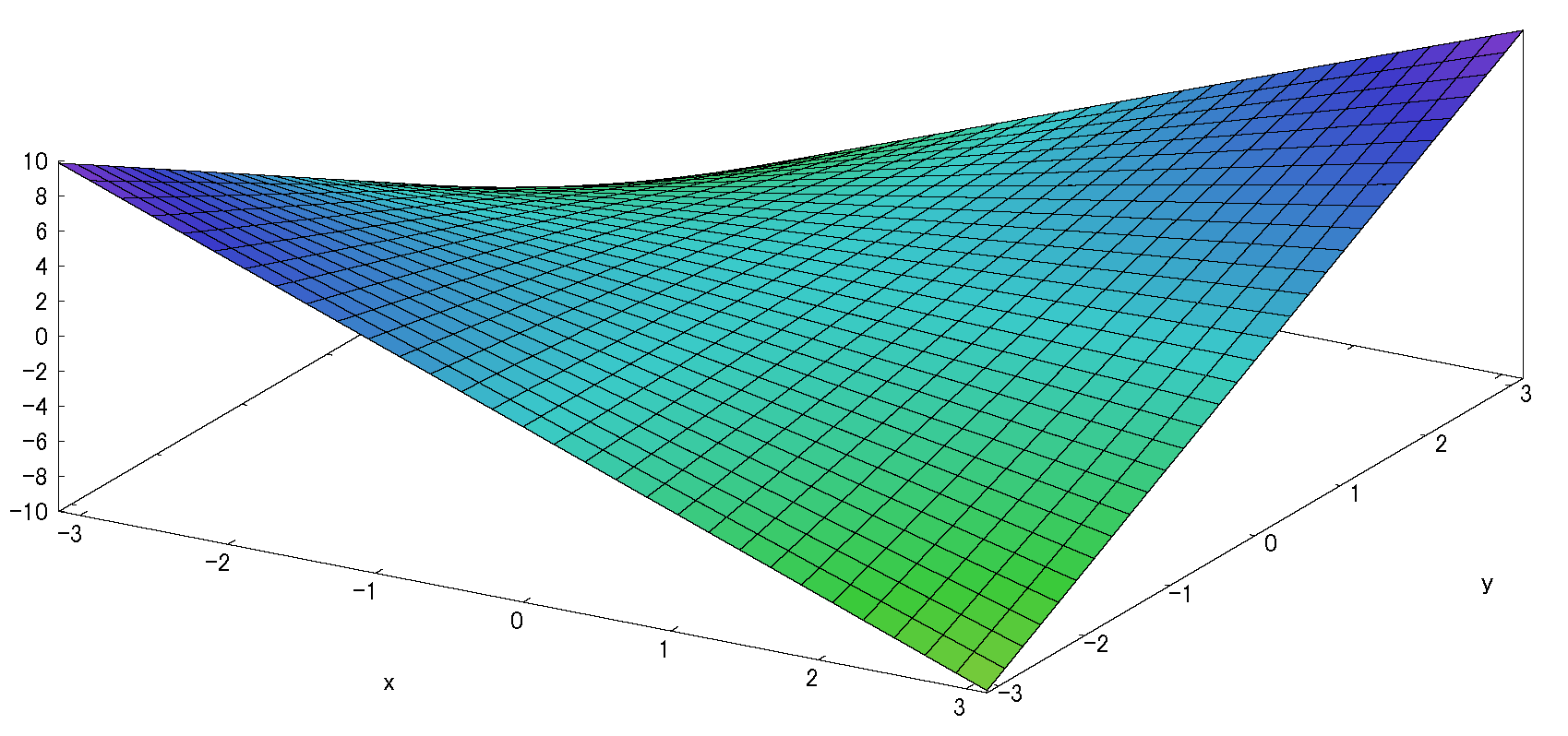
\(\therefore f(x,y)=2(x^2+x-y^2-4)\)
:(fig2.3)
\(f(x,y)=4y-4y-2\)
\(f_x(0,0)=e^y \frac{1}{1+x}=e^0 \frac{1}{1+0}=1\) \(\ ,\ \) \(f_{xx}(0,0)=e^y \frac{-1}{(1+x)^2}=-1\) \(\ ,\ \)
\(f_{xxx}(0,0)=e^y \frac{2}{(1+x)^3}=2\)
\(f_y(0,0)=f_{yy}=f_{yyy}\)\(=e^y log(1+x)=0\)
\(f_{xy}(0,0)=f_{yx}\)\(=e^y \frac{1}{1+x}=1\)
\(f_{xxy}(0,0)=f_{xyx}=f_{yxx}\)\(=e^y \frac{-1}{(1+x)^2}=-1\)
\(f_{yyx}(0,0)=f_{yxy}=f_{xyy}\)\(=e^y \frac{1}{1+x}=1\)
\(f(0,0)=e^y log(1+x)=0\)
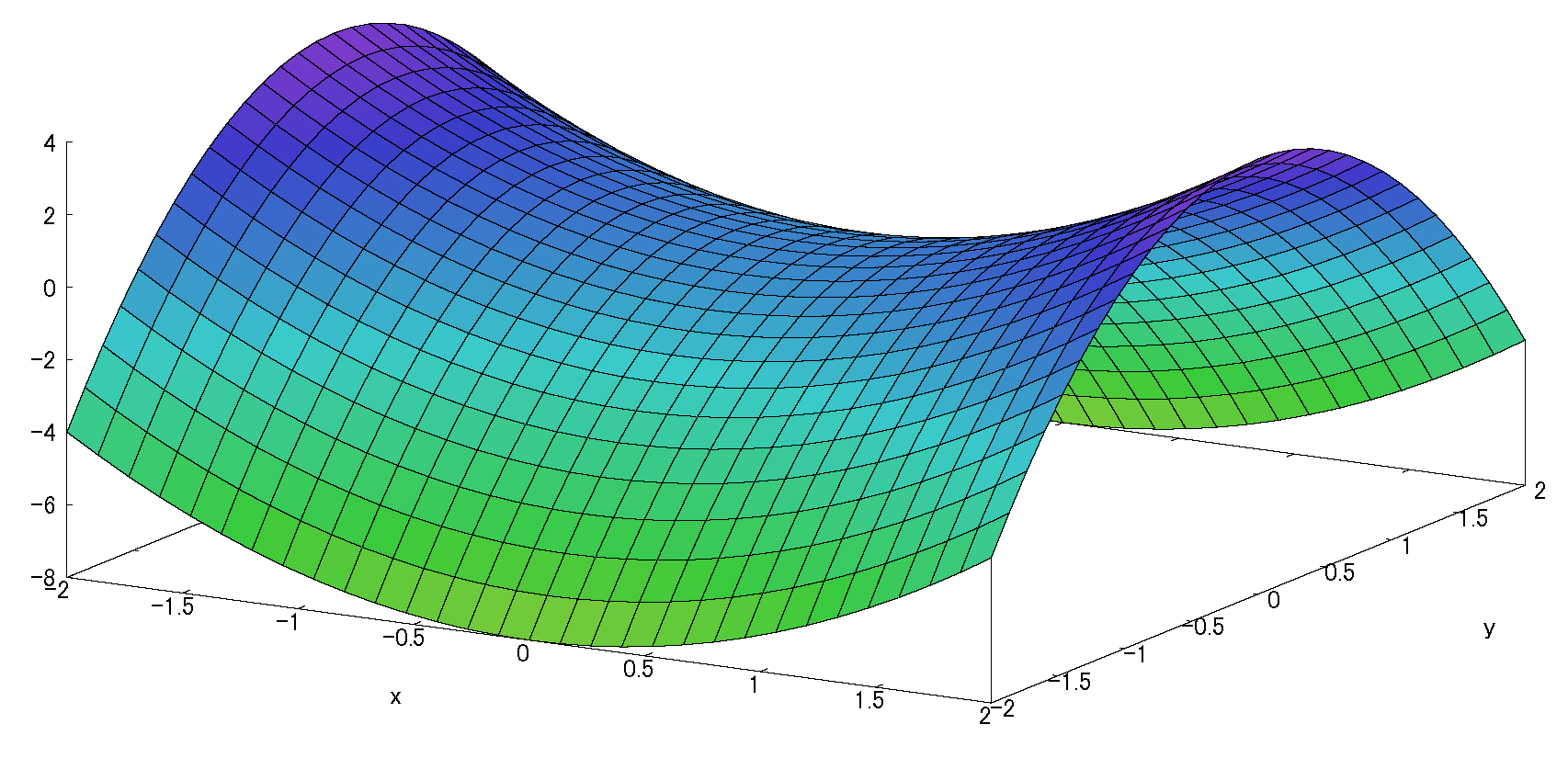
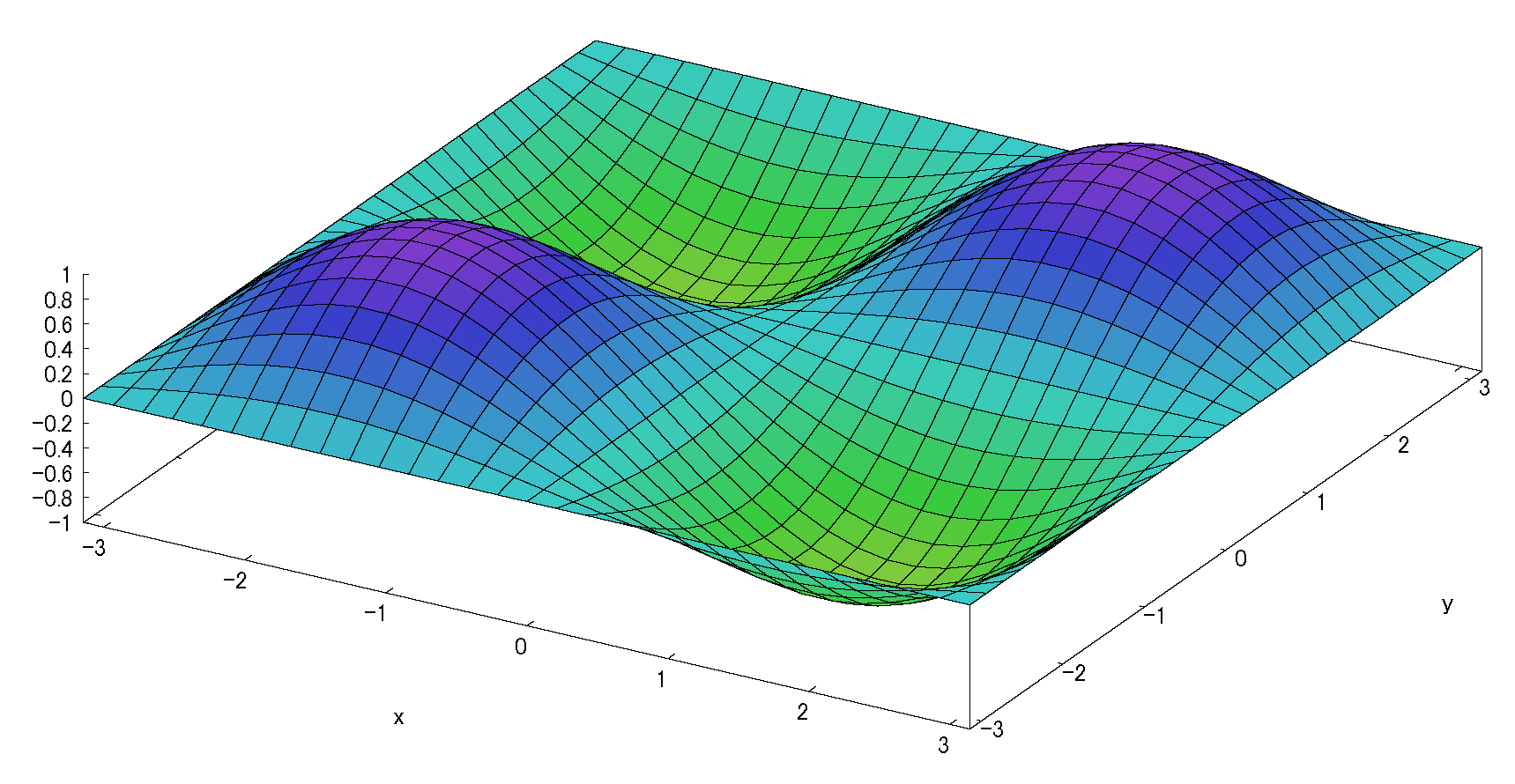
\(\therefore f(x,y)=x\)\(+[\frac{1}{2}(-x^2+2xy)]\) \(+[\frac{1}{6} (2x^3-3x^2y+3xy^2)] \)(※1)
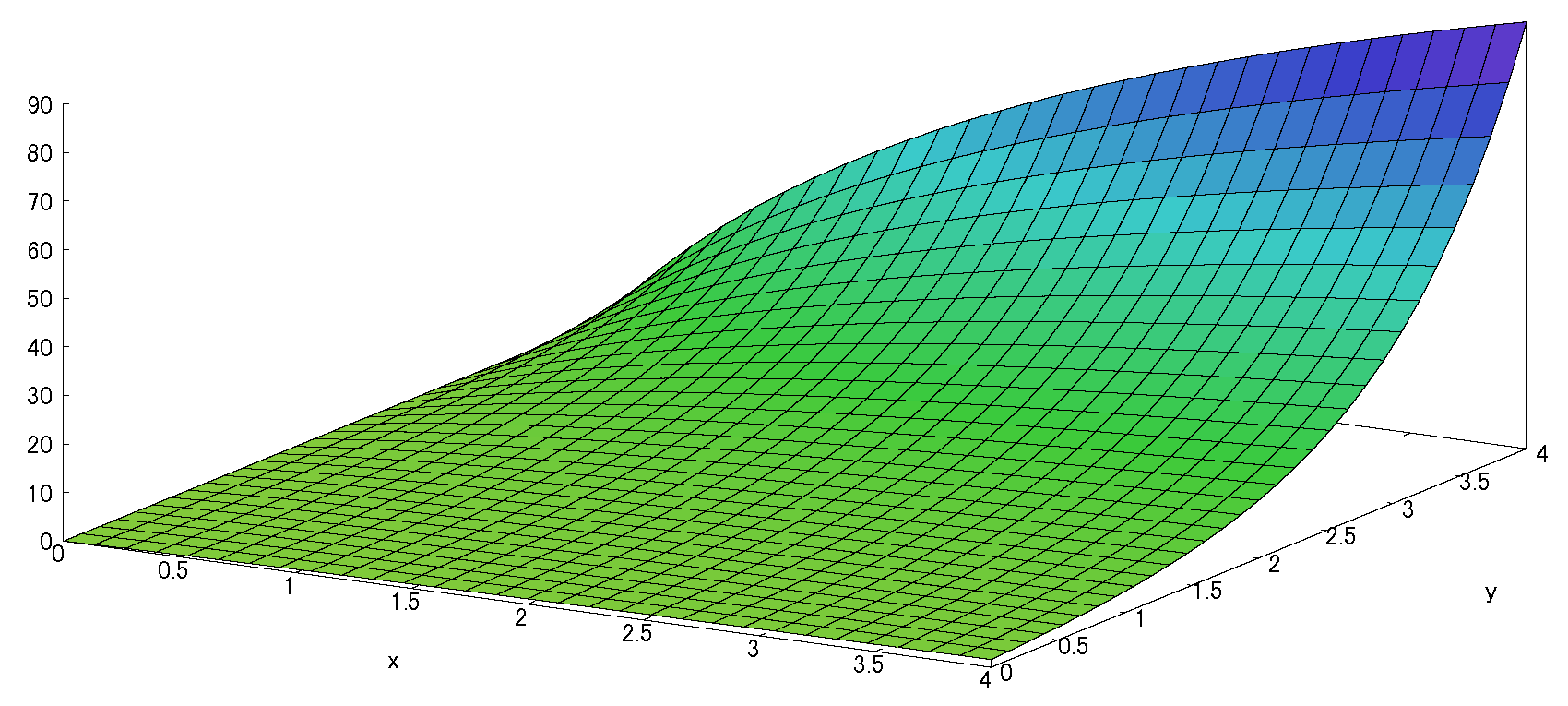
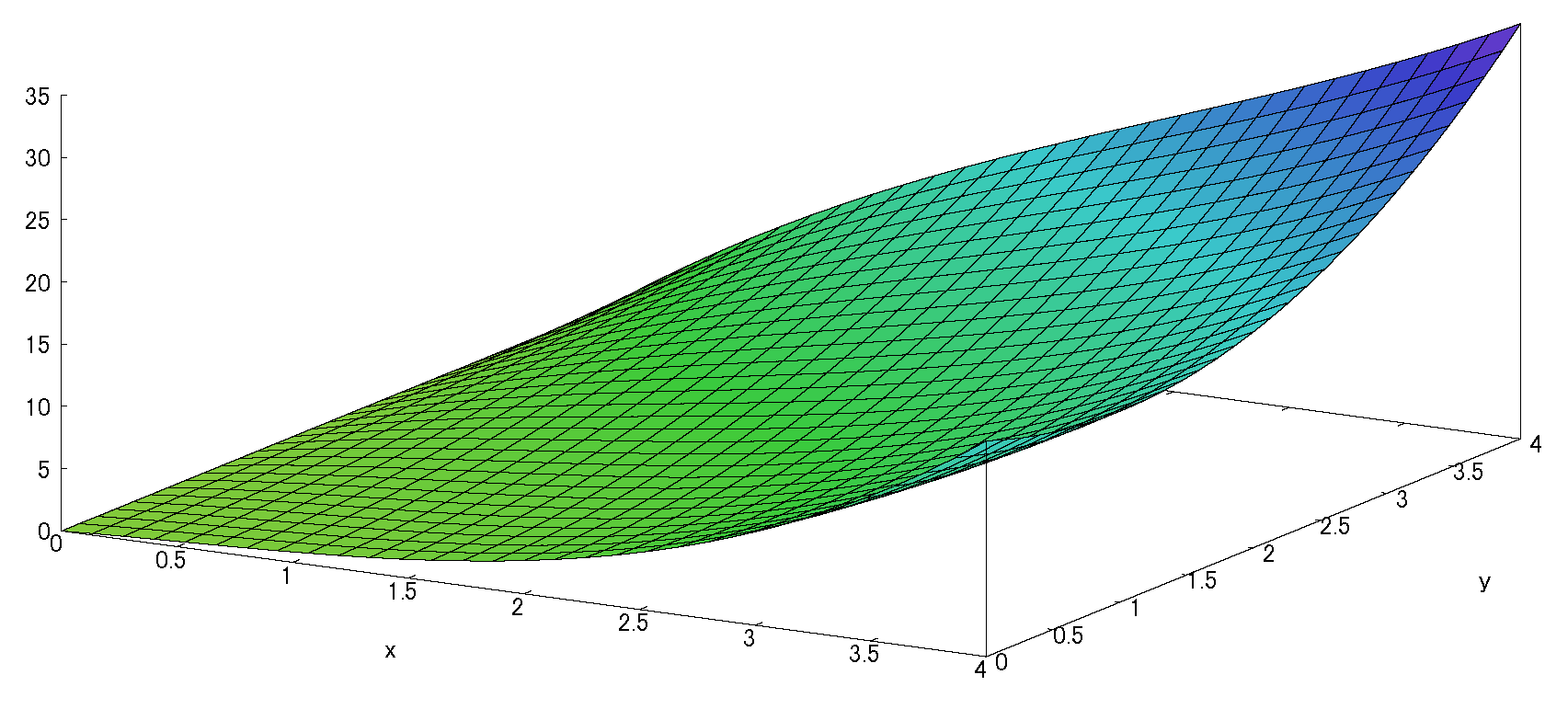
注:1次近似は「0」だから接平面の傾きが「0」、すなわち「x軸-y軸平面」の水平面である。
(以下の図(fig)に接平面がないのは同様に理由です。)
\(f_x(0,0)=y\ cosxy=0\) \(\ ,\ \) \(f_y(0,0)=x\ cosxy=0\)
\(f_{xx}(0,0)=-y^2\ sinxy =0\) \(\ ,\ \) \(f_{yy}(0,0)=-x^2\ sinxy=0\)
\(f_{xy}(0,0)=cosxy-xy\ sinxy=1\) \(\ ,\ \) \(f_{yx}(0,0)=cosxy-xy\ sinxy=1\)
\(f_{xxx}(0,0)=-y^3\ cosxy=0\) \(\ ,\ \) \(f_{yyy}(0,0)=-x^3\ cosxy=0\)
\(f_{xxy}=-2y\ sinxy-xy^2cosxy=0\) \(\ ,\ \) \(f_{yyx}=-2xsinxy-x^2y\ coxxy=0\)
以下のように下線以外の項は「0」である。
\(\underline{f(x,y)}=f(0,0)\)
\(+[xf_x(0,0)+yf_y(0,0)]\)
\(+[\frac{1}{2}(x^2 f_{xx}(0,0)+\underline{2xyf_{xy}(0,0)}\)\(+y^2f_{yy}(0,0))]\)
\(+\frac{1}{6} (x^3f_{xxx}(0,0)+3x^2yf_{xxy}(0,0)+3xy^2f_{xyy}(0,0)\)\(+y^3f_{yyy}(0,0))\)
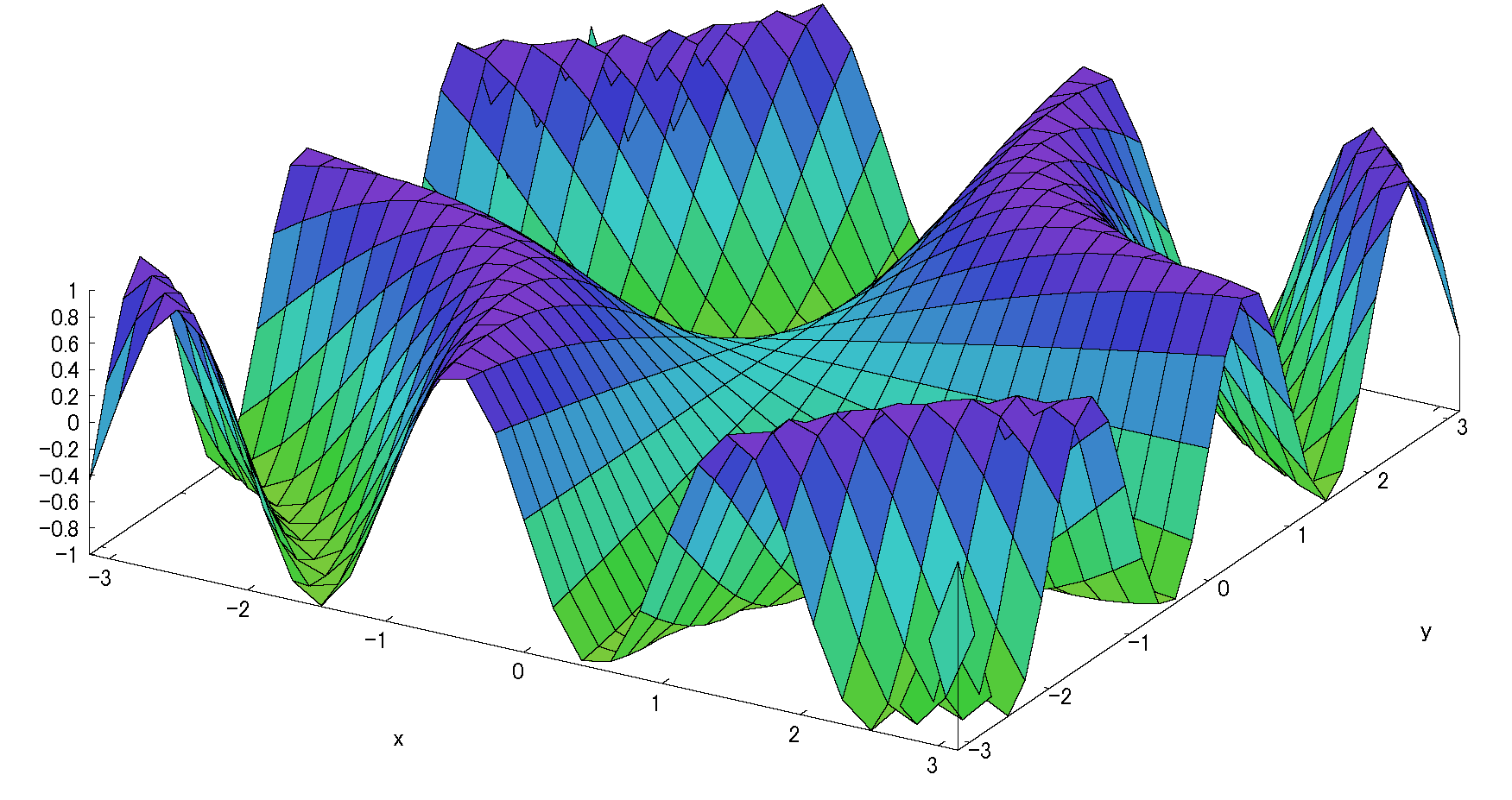
\(f_x(0,0)=cos x\ sin y=0\) \(\ ,\ \) \(f_y(0,0)= sinx\ cos y=0\)
\(f_{xx}(0,0)=-sin x\ sin y=0\) \(\ ,\ \) \(f_{yy}(0,0)=-sin x\ sin y=0\)
\(f_{xy}(0,0)=cos x\ cos y=1\) \(\ ,\ \) \(f_{yx}(0,0)=cos x\ cos y=1\)
\(f_{xxx}(0,0)=-cos x\ sin y=0\) \(\ ,\ \) \(f_{yyy}(0,0)=-sin x\ cos y=0\)
\(f_{xxy}=-sin x\ cos y=0\) \(\ ,\ \) \(f_{yyx}=-cos x\ sin y=0\)
\(f_{xxxx}(0,0)=sin x\ sin y=0\) \(\ ,\ \) \(f_{yyyy}(0,0)= sin x\ sin y=0\)
\(f_{xxxy}(0,0)=-cos x\ cos y=1\) \(\ ,\ \) \(f_{yyyx}(0,0)=-cos x\ cos y=1\)
\(f_{xxyx}(0,0)=-cos x\ cos y=1\) \(\ ,\ \) \(f_{yyxx}(0,0)=sin x\ sin y=0\)
4次項
\(=\frac{1}{4!} [x^4f_{xxxx}(0,0)\) \(+4x^3y f_{xxxy}(0,0)+6x^2 y^2f_{xxyy}(0,0)\)\(+4xy^3f_{yyyx}(0,0)+y^4f_{yyyy}(0,0)]\)
\(=\frac{1}{24} [0 - 4x^3y\cdot 1 \)\(+ 0 - 4xy^3\cdot 1 + 0 ]\)
\(=\frac{1}{6} [-x^3y - xy^3 ]\)
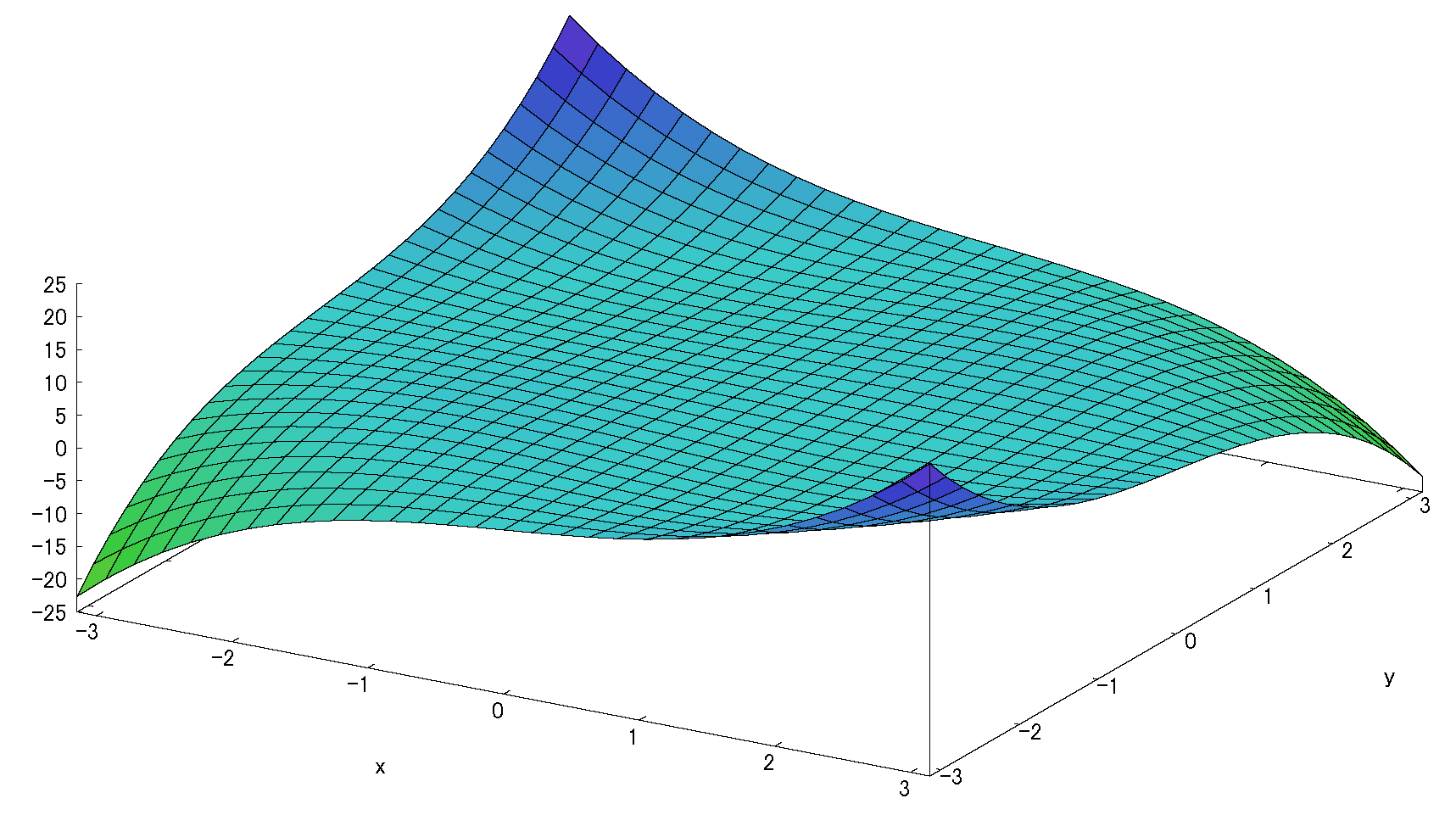
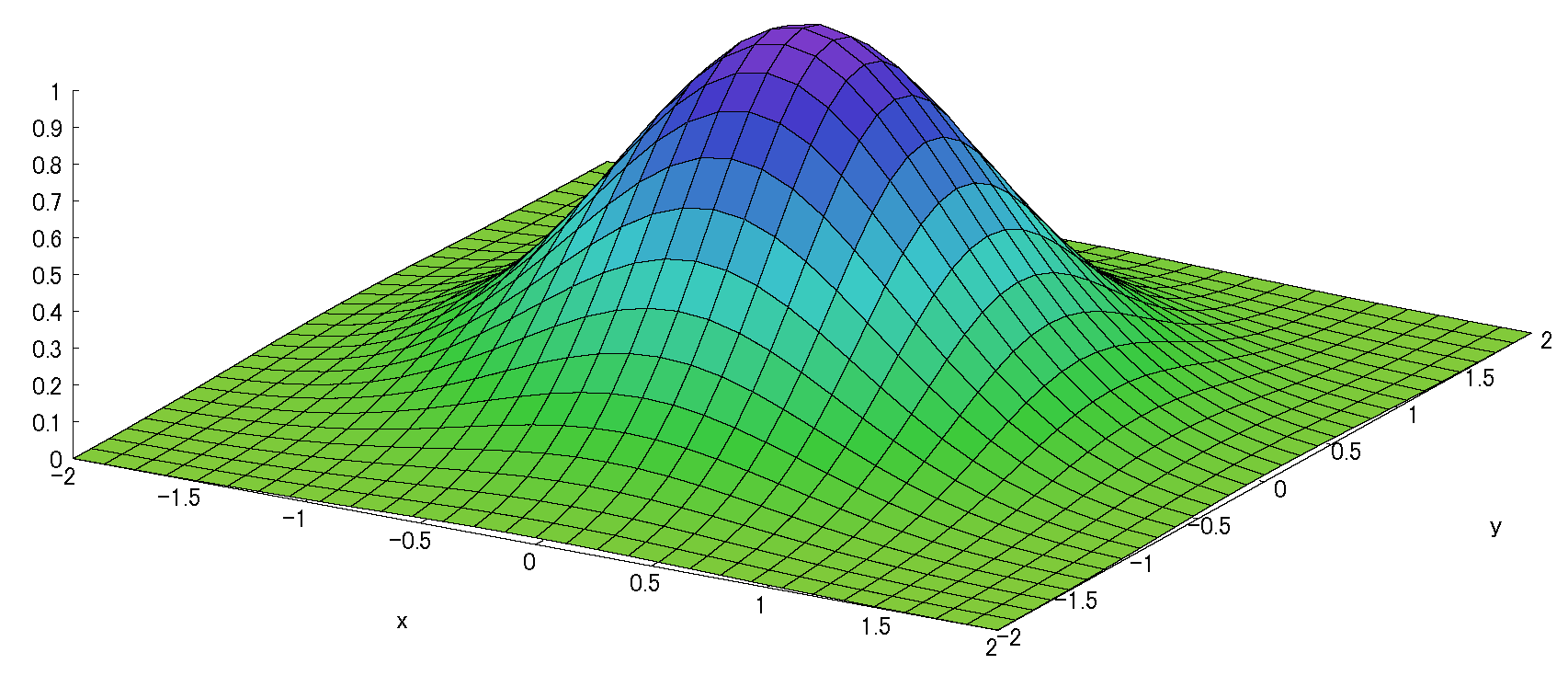
\(u=-(x^2+y^2)\)とする。(表記の簡略のために)
\(f_x(0,0)=-2xe^u=0 \) \(\ ,\ \) \(f_y(0,0)=-2ye^u=0\)
\(f_{xx}(0,0)=-2e^u+4x^2e^u=-2\) \(\ ,\ \) \(f_{yy}(0,0)=-2e^u+4ye^u=-2\)
\(f_{xy}(0,0)=4xye^u=0\) \(\ =\ \) \(f_{yx}\)
\(f_{xxx}(0,0)=12xe^u-8x^3e^u=0\) \(\ ,\ \) \(f_{yyy}(0,0)=12ye^u-8y^3e^u=0\)
\(f_{xxy}(0,0)=4ye^u-8x^2ye^u=0 \) \(\ ,\ \) \(f_{yyx}(0,0)=4xe^u-8xy^2e^u=0\)