この定理の主張は「上図のうように閉区間の列を縮小(これを減少列と呼ぶ)していき、その減少列が0 に収束するとき、その減少列はすべての閉区間に属する1 点 αに収束すること」である。

閉区間の列\(I_n=[a_n,b_n] \) \((n=1,2,3,\cdots)\) において、

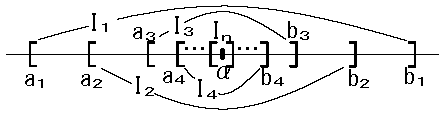
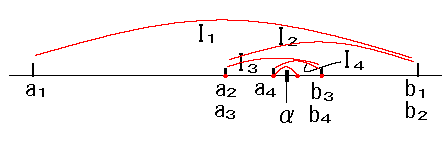
1)\(I_1 \subset I_2 \subset I_3 \cdots\)
2)\(\displaystyle \lim_{n \to \infty}(b_n-a_n)=0\)

ならば、これらはすべての閉区間に属するただ1つの点α が存在し、

\(\displaystyle \lim_{n \to \infty}a_n = α =\displaystyle \lim_{n \to \infty}b_n\) である。

　

実数の切断(A,B) があって、境界はmaxA か minB のいずれかです。
閉区間\([a_1,b_1]\)の中点C をとり、この中点C がA に属するかB に属するか調べる。
中点C は\(C=\frac{a_1+b_1}{2}\) で求められる。
\(I_1=[a_1,b_1]\quad\)\((a_1\in A,b_1\in B)\)
すなわち 縮小1 の\(I_1\)は次のいずれか

\(C\in A:\) \(a_2=\frac{a_1+b_1}{2}\) \(\ , b_2=b_1\)
↑上図場合
\(C\in B:\) \(b_2=\frac{a_1+b_1}{2}\) \(\ , a_2=a_1\)

つぎの縮小2 の\(I_2\)：

\(C\in A:\) \(a_3=\frac{a_2+b_2}{2}\) \(\ , b_3=b_2\)
\(C\in B:\) \(b_3=\frac{a_2+b_2}{2}\) \(\ , a_3=a_2\)
↑上図場合

中点C がA組にいれば、次の中点はB 組に行く方向にいくようにする。
こうすると閉区間\(I_n\)がジグザグにしながら縮小し、切断(A,B) 点に近づく。

すなわち

\(I_1\subset I_2\subset \cdots \subset I_n \cdots \)
\(b_n-a_n=\frac{b_1-a_1}{2^{n-1}}=0\)　:➀　\(\quad (n\to \infty) \)

上式が0 となるのはアルキメデスの公理に基づきます。（後述します【※3】 ）

上記の無限回の縮小の収束先はαです。
したがい、区間縮小定理より、すべての閉区間\(I_n\) に属するただ1点αが存在し

\(\displaystyle \lim_{n \to \infty}a_n = α =\displaystyle \lim_{n \to \infty}b_n\)

であり、次の関係を最確認すと：

\(a \lt b\) \(\quad \) \(a_n\le α \le b_n\)
\(α\in A\) \(\ or \) \(α\in B\)である。

以下は

\(α\in B\)として\(x\gt α\)　\((x\in B)\) として考える。
\(\displaystyle \lim_{n \to \infty}(b_n-a_n)=0\)です。

ここで任意の\(ε\) が存在し、あるm が存在し\(n \gt m\) に対し \(b_n-a_n\) が\(ε\) 未満となる。

\(ε_1=\frac{x-α}{2}\) とする。
この\(ε_1\)に対し\(n\ge N_1\) が存在して　\(b_n-a_n \lt ε_1\)
\(b_{N1}\lt a_{N1}+ ε_1 \le α + ε_1\) \(=α+\frac{x-α}{2}=\frac{x+α}{2}\)\(\lt \frac{2x}{2}=x\)
これより\(b_{N1}\lt x\)

\(\therefore\)\(α\in B\) と、上記より \(α=min B\) である。　

【※3】:アルキメデスの公理により 式➀ が0 となる根拠