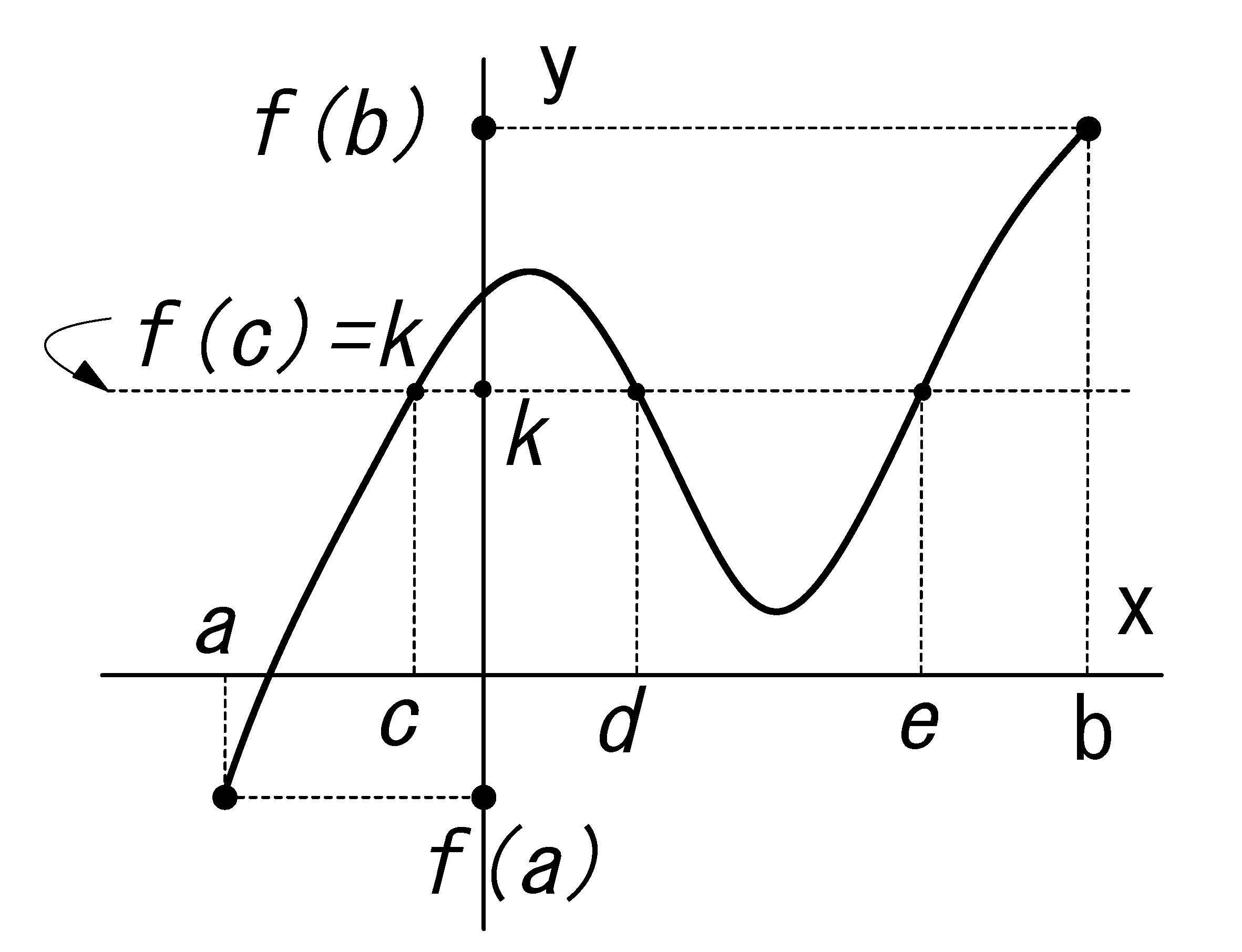
|
【中間値の定理】
関数 f(x) が閉区間 [a, b ] において連続とします。
\( f(a) \ne f(b) \) (図では \( f(a) <f(b) \) )ならば: \(f(a)\) と \(f(b)\) の間に ある k に対して、 \( f(c)=k \) を満足する c が a-b 間に少なくても 1 つは存在する。 |
上図では\( f(a) <f(b) \)であるが、\( f(a) \gt f(b) \) であっても、その中間に\(k\) があって、その\(k\) に対応する\(c\) が少なくても1 つ存在することです。
図のとおり複数存在してもよいです。
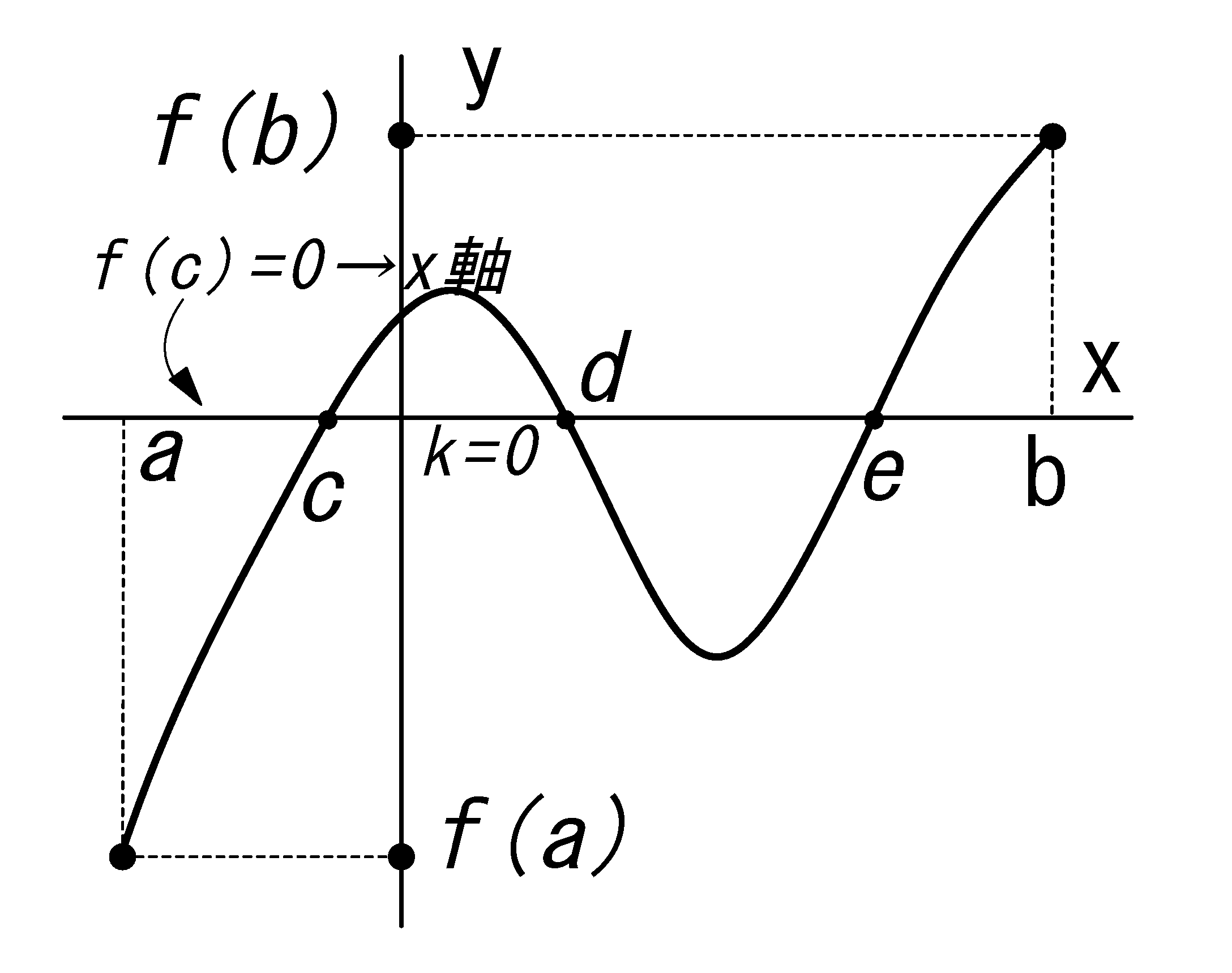
|
【中間値の定理(特殊形)】
関数 f(x) が閉区間\([a, b ]\) において連続とします。
\(f(a)\) と \(f(b)\) が異符号なら 関数\(f(x)\) は x 軸と交差する。 このことは閉区間\([ a, b ]\) において、\(f(x)\) は実数解をもつことである。 (1項の中間値定理の\( f(c)=k\)を\(\rightarrow f(c)=0\) に対応したのと同じ ) |
|
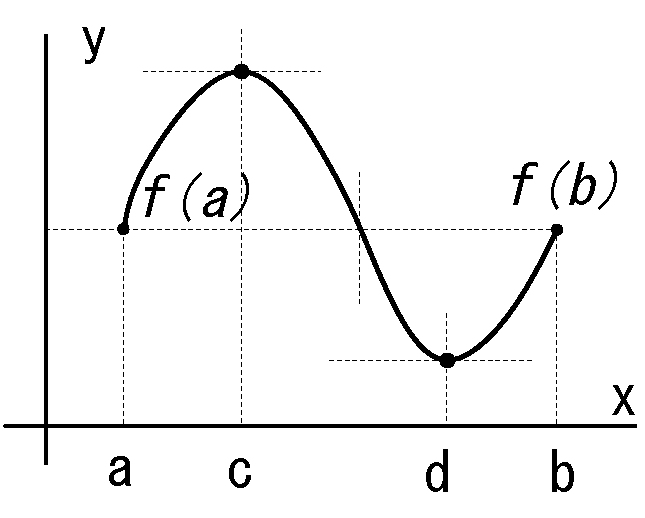
【ロルの定理】
関数 f(x)が閉区間\([a, b ]\) において連続とします。
・閉区間 \((a, b )\) で微分可能。(※1) ・\(f(a)=f(b)\) であるとき \(f'(c)=0\) (1階微分) を満足する\( c \) がすくなくても 1つ存在する。 |
|
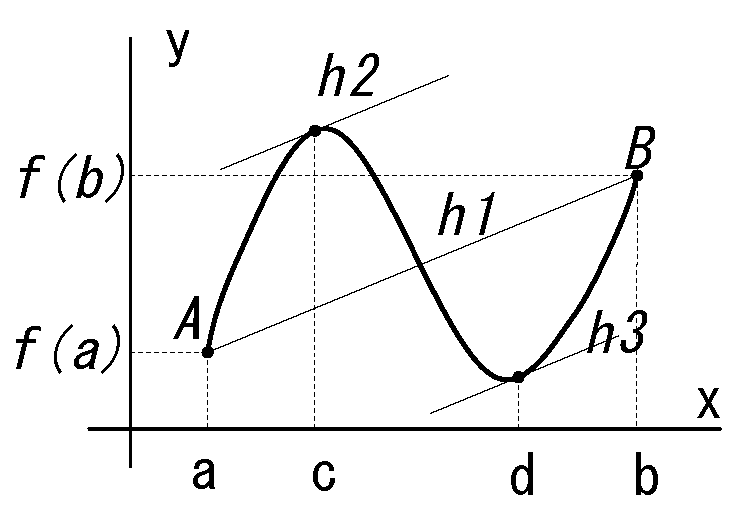
【平均値の定理】(ラグランジュの平均値の定理)
関数 f(x)が
・閉区間 \([ a, b ]\) において連続。 ・開区間 \((a, b )\) で微分可能。 のとき、関数 f(x)に対し、 \( \frac{f(b)-f(a)}{b-a}=f'(c) \) を満たす \(c\) が 開区間 \((a,\ b)\)(※1) に少なくても1つ存在する。 (直線 AB と同じ傾きをもつ接線 \(f'(c)\) となる x 軸上の点 \(c\) が必ず1つ存在する) (※1:\(a<c<b\) ) |
|
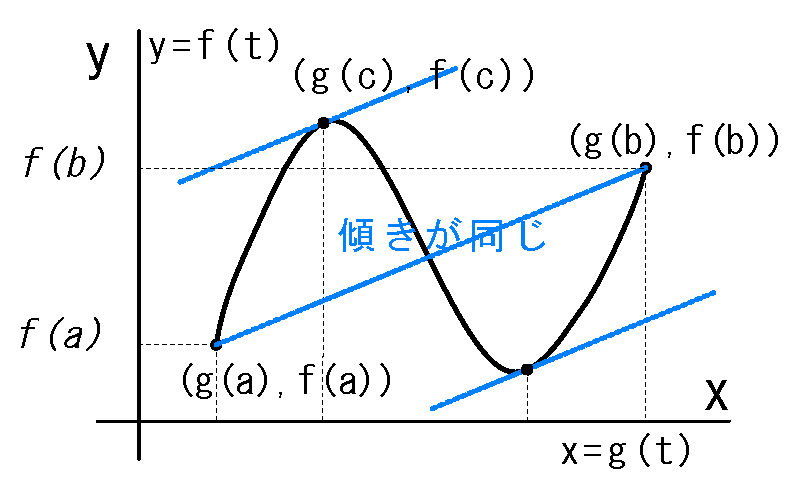
【コーシーの平均値の定理】
関数 f(x) と g(x) が
・閉区間 \([ a, b ]\) において連続。 ・開区間 \((a, b )\) で微分可能。 ・\(g'(x)\ne 0\) ・\(g(b)-g(a)\ne 0\) のとき、関数 f(x), g(x) に対し、 \( \frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f'(c)}{g'(c)} \) を満たす \(c\) が 開区間 \((a,\ b)\)(※1) に少なくても1つ存在する。 (言い換えると、点\(c\)において 両端点を結ぶ直線と同じ傾き(\( \frac{f'(c)}{g'(c)}\))の接線が1つ以上存在する) (※1:\(a<c<b\) )
注:\(g(x)=x\)とおくと「コーシーの平均値」は「ラグランジュの平均値」に帰着する。
∵\(g(x)=x\)とおくと
\(g'(x)=1,\ g'(c)=1\)
\(,\ g(b)=b,\ g(a)=a\) |