湘南理工学舎・解析学・実数の連続性

はじめに

実数の連続性を当たり前のようにして受け入れて微分積分を学んできました。
実数の連続性の証明は遠い昔ではなく19世紀後半です。ここにデデキントをはじめカントール、ワイエルシュトラスが登場します。
整数、有理数に無理数が加わったのが実数ですが、この無理数はピタゴラスの定理により\(\sqrt{1^2+1^2}=\sqrt{2}\) が得られます。
ピタゴラスは紀元前500年、無理数を加えた実数を証明し公理となったのは1800年代の後半です、長い年代がかかっています。

実数の連続の証明の歴史に対して、微分積分学ではどうか…微分についての極限の概念は紀元前、積分の基礎は10世紀ごろ始まり近代にはいり、17世紀において、ニュートンをはじめとする数学者により微分積分学の統合が行われた。

これからデデキントの切断公理により実数の連続性を解説していきます。
（この公理を「連続の公理」,「デデキントの連続公理」,「実数の連続性公理」などと呼んでいます）

切断とは

すべての数をA,B の二組の集合に分けて、A に属する各数をB に属する各数より小さいとすると、この組(A,B) をデデキントの切断いう。
A組を下組、B組を上組といい、どんな数も、もれなく下組か上組のいずれか一方にのみに属する。
これをもっと具体的に言うと：
・集合A、B は空集合ではない
・AとBの共通部は空集合である。
・A組の元a 、B組の元b に対し \(a \lt b\)である。
ここではまだ、数は 有理数\(\bm{ Q }\) か実数\(\bm{ R }\) は決めていない。
（以下では実数\(\bm{ R }\)で表現している)
切断を集合の記号を用いて表現するなら以下となる（実数を例にすると）
(A,B) が数の切断とは： (実数\(\bm{ R }\)を例にして)

1)\(A \ne \emptyset \ , \ B \ne \emptyset\)

A,B 空集合ではない

2)\(A∪B=\bm{ R } \ , \ A∩B＝ \emptyset\)

A,Bの和集合は実数
A,Bの共通は空集合 (A とB は互いに交わらない)
いずれの元も、A組かB組のいずれかに属す

3)\(\forall a\in A\) かつ　\(\forall b\in B\)　に対し \(a \lt b\)

A の任意の元a とB の任意の元b について \(a \lt b\)

このとき (A,B) を実数 \(\bm{ R }\) の切断(A,B)という。
(または有理数\(\bm{ Q }\) の切断(A,B)という。)

これから切断の境界の最大数(最小数)について論じるので、最大値(最小値)について復習しおこう。

集合A の最大値(最小値)とは（参考）

\(a\in A\) かつ \(\forall x\in A\) に対し \(x \le a\)(\(x \ge a\))のとき
a が集合A の最大値(最小値)という。

(a はA の元　そしてA内の全ての数に対して a が最大のとき)

☞ポイント 最大値a とはA の元、A に属していること。

次の例で確認しよう。

・閉区間A=[1,2]=\(1\le x \le2\)　

集合A に1,2 を含むから最小値=1、最大値=2がある。

・開区間A=(1,2)=\(1\lt x \lt2\)

有界であるが集合A に1,2 を含まないから最大値、最小値はない。

fig1 最大値・最小値

次に進む前に少し考察しましょう。
一般に「数が連続」の直感的な表現は「数直線に穴がないこと」といわれています。
これを数学的に表わさなければならない。
数が連続とは一般に上記切断パターンの 1）、2) のことです。
また「実数の連続の公理」（デデキントの連続公理）は上記の切断パターンの 1）、2) のいずれかが成立することです。
この公理について後半に詳しく述べます。

はじめに有理数の切断について：
有理数の切断

1)、2)は数が連続の状態です。分かり易く表現すると：
境界点の数をC としてC がA組か B組のどちらかにある切断です。
1)はC がA組の元にあるとき、すなわち次の状態のとき：

・C 以下の数がA組、Cより大きい数がB組のとき
・A組とB組= (-∞,C ] ( C,∞ )

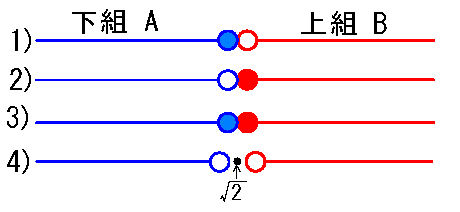
A組はC で右半閉区間、B組はC で左半開区間

2)はC がB組の元にあるとき、すなわち次の状態のとき：

・C より小さいの数がA組、C以上数がB組のとき
・A組とB組= (-∞,C ) [ C,∞ )

3)は起こりえない切断です…これを背理法で証明します。

・a=max A かつ b=min B が存在すると仮定すると：
・切断の定義の \(a\in A\ と\ b\in B \),\(\ a\lt b\) に対して有理数の稠密性より \(a\lt C\lt b\) なる\(C\) が存在する。
・このC は A より大きいのでA には属さない。またB より小さいのでB にも属さない。
・これは切断の定義の2) に矛盾する。
☞ポイント

a) C はA かB のいずれかに属すこと。
b) A∩B＝\(\emptyset\) 共通部は空(A とB は交わらない)

4)は起こりえる切断です
次の場合を考える

\( \begin{cases} A組：2乗して2より大きい有理数\ かつ x\gt 0)\\ B組:A組以外の有理数 \end{cases} \)
記号で表すと:
\( \begin{cases} A=\{x\in \bm{ Q }|x^2\gt 2\ かつ x\gt 0\}\\ B=\bm{ Q } \setminus A\quad (B=Q-A:差集合)\\ \end{cases} \)
この場合、境界にある数\(x^2=2\) であり…有理数にはない数で、有理数の数直線では穴が開いています。
これは無理数の\(\sqrt{2}\)です。
そこで稠密な有理数にさらに、稠密な無理数を加えた実数が登場します。

次に実数の切断について：
実数の切断

切断による境界のパターン 1),2),4) は有理数の切断と同じです。
注目すべきは 4)の「A組に最大数がなく、B組に最小数がない」ことです。
有理数は稠密性により数直線を埋め尽くし、実数はさらに無理数が加わり数で詰まっていて充実しているはずです。
疑問は実数の間に、新しい数が存在し、実数の切断において4) の場合があるか、どうかです。
答えは次の「連続の公理（別名：デデキントの連続公理」です。
（公理なので、証明なしで受け入れるのが一般です）
以下はデデキントの連続公理にくわえ、実数に関連した公理です。

実数の公理
次の4つ公理を満たす集合\(\bm{R}\) を実数体といい、その元を実数という。
1.連続の公理（デデキントの公理）

実数の切断(A,B)において、次のいずれかが成立する。
1)A組に最大数があり、B組には最小数がない。
2)A組に最大数がなく、B組には最小数がある。
これは実数が連続であることを示している。

2.四則演算に関する性質

実数において0 による除法を除いて、加減乗除の四則演算は自由に行える。
（これを実数の体を作るという）

3.大小の順序に関する性質

実数は次の大小関係をもつ
1)任意の2元 a,b の間には
a>b a=b a<b
のうちただ一つの関係だけが成り立つ。

2) a>b, b>c ならば　a>c　である。

4.大小の順序と演算に関する性質

大小の順序と演算について次が成り立つ
1) a>b ならば a+c>b+c　
2) a>b, c>0 ならば ac>bc

5.アルキメデスの公理

任意の正の定数 h , 任意の正の数 K に対して
　nh > K
となる自然数がn が存在する。(※)

(※)アルキメデスの公理の説明

・公理なので証明しませんが、「2つの正の数 h,k があるとき、h を何倍(n)かすると、いつかはk をこえる」との意味。
・論理記号表示では:
\( \forall k>0 ,\quad \exists N>0, \ s.t.　\ n>N\) \(\Rightarrow nh>k \) \(\ :❶\)

任意の正の数k に対して、\(n>N\)ならば、\(nh<k\)　となるN が存在する

最後に一言:
偉大な数学者が実数の連続性を証明し、公理にしたのだから、我々はそれを利用して先に進むのも、よいことでしょう。

参考図書：田島一郎、「解析入門」　岩波書店　　

coffe

[コーヒーブレイク/閑話］…お疲れ様でした。