楽しく学ぶ…熱力学
束縛エネルギー\(~\rm TS~\)項の意味
納得の行く説明が見当たらない。どこまでできるかやってみよう。
束縛エネルギー\(~\Vec T\Vec S\) 自由に取り出せないエネルギーであるが。
一般的な説明 大変分かり難い。\(TS~\)は取り出せるのか取り出せないのか?
自由エネルギーは熱機関というよりも,「平衡系の熱力学」への応用の方が有意義であるが, ここでは話を簡単にするために熱機関で考えよう。
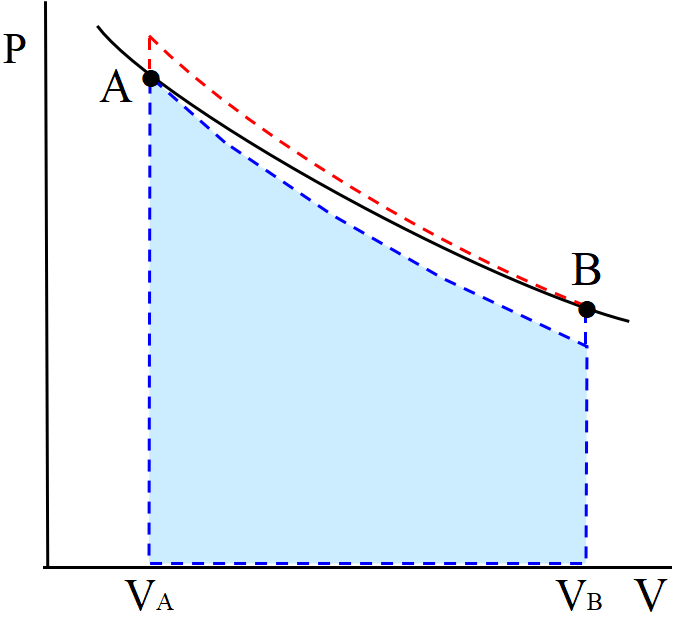
\(~A\to B~\)の等温膨張過程で
熱機関から取り出せる最大のエネルギーは,
\[F=U-TS \tag{1}\]
であった。これを\(~U=F+TS~\)として, 内部エネルギーは,
\(\quad\)自由に取り出せる自由エネルギー\(~F~\)と,
\(\quad\)自由に取り出せないエネルギー\(~TS~\)
から成り立っている, と説明される。後者を「束縛エネルギー」あるいは稀に「不自由エネルギー」と呼ぶ。
熱機関が等温膨張する時の様子を再確認しておこう。
一般に膨張過程では温度が下がるから熱浴からピストンへ熱が流れ込む。等温過程では, 膨張によって外界へ仕事をした, すなわち減少した内部エネルギーは, 流れ込んだ熱量で完全に補われ, 結局内部エネルギーは変化しない。
「内部エネルギーのうち, 取出せるエネルギーを自由エネルギーという」と表現されるが, 等温膨張では内部エネルギーは全く取り出されず, 更に正確に言えば取り出す必要もなく, 流入した熱量が仕事に変わっただけである。燃焼させた石炭の熱が仕事に変わるわけだから, 熱機関としては至極当然のことである。
もっとも, 先ず内部エネルギーにより膨張し, すかさず熱浴から熱が流入するから「内部エネルギーが取り出された」と言えなくもないが, 些末な議論であろう。ともかく「内部エネルギーは変化していない」。ばねの伸縮による弾性エネルギーとは異なる。
(1)式の全微分を取れば,
\[dF=dU-TdS-SdT \]
内部エネルギーは変化していないから\(~dU=0\), 等温過程であるから\(~dT=0~\)。従って,
\[dF=-TdS \]
外部に仕事をした分だけ失われたのは自由エネルギー\(~F~\)である。ここのところは教科書, ネット記事同じである。
そして\(~\varDelta F~\)はエントロピーに起因する熱量, \(T\varDelta S(=T\x \varDelta Q/T=\varDelta Q) ~\)である。ここの記述がバラバラである。
殆どは\(~T\varDelta S~\)は取出せないエネルギー, あるいは温度を維持するために必要なエネルギーと説明される。
因みに\(~A\to B~\)の等温膨張でのエントロピー変化は,
理想気体のエントロピーの繰り返しになるが, 熱力学第一法則より,
\[d'q=dU+pdV=nC_V dT+\frac{nRTdV}{V} \]
積分因子\(~1/T~\)を乗ずると,
\[dS=\frac{d'q}{T}=\frac{nC_V dT}{T}+\frac{nRdV}{V} \]
となる。これを積分すると,
\[\varDelta S=S(B)-S(A)=\int_{A}^{B}nC_V\frac{dT}{T}+\int_{A}^{B}nR\frac{dV}{V}\]
となり状態量\(~S\), エントロピーが算出される。等温過程では\(~T_A=T_B~\)より右辺積分第一項は消えて
\[\varDelta S=nRlog\frac{V_B}{V_A} \]
と算出される。これに\(~T~\)を乗じた\(~T\varDelta S~\)が外部へ取出された自由エネルギーである。
「\(TS~\)項は自由に取り出せないどころではなく, 外部へ為す仕事の源泉である」と筆者は考えるが, あまり見かけない議論である。
金属結晶格子欠陥 \(~\rm TS~\)項は
ヘルムホルツ自身による電池の説明では分かり易いが, 理想気体で考察するのは難しい。
熱力学の特徴として, その抽象性が挙げられる。現象の捉え方が曖昧としている反面, 原子が数十個から宇宙大までの神羅万象を記述する。
ただヘルムホルツの自由エネルギー\(~F=U-TS\), ギブスの自由エネルギー\(~G=H-TS~\)の\(~TS~\)項については抽象的な議論では中々納得が得られない。少なくとも筆者はそうであった。
抽象的な言葉で説明するより, 実際の物質について計算で示した方が理解し易い。ここでは金属結晶中の格子欠陥\(~(lattice\; defect)~\) を考えて見よう。
原子空孔 最も基本的な金属結晶格子欠陥
今までは全て理想気体を対象として議論してきた。金属結晶の格子欠陥は, 固体で混合エントロピーの使える数少ない例である。自由エネルギーの\(~TS~\)項の説明については理想気体よりも適しているように感じており, 取上げることとする。
金属結晶は原子が整然と並んでいるわけでは無く, 何らかの不規則, 欠陥がある。
欠陥には図のような点欠陥の他に, 面としてずれる線状の欠陥, 転位\(~(dislocation)~\)がある。詳しくは材料科学等の教科書を参照されたい。
結論から言ってしまうと, 融点近くの金属で, 格子欠陥個数\(~n~\)は基層原子に対し, 空孔は\(~\sim 10^{-4}~\)程度, 自己格子間原子は\(~\sim 10^{-11}~\)程度であり, 空孔\(~(vacancy)~\)を考えれば十分である。空孔は別名ショットキー\(~(Schottky)~\)欠陥とも呼ばれる。
空孔形成エネルギーと空孔移動エネルギー
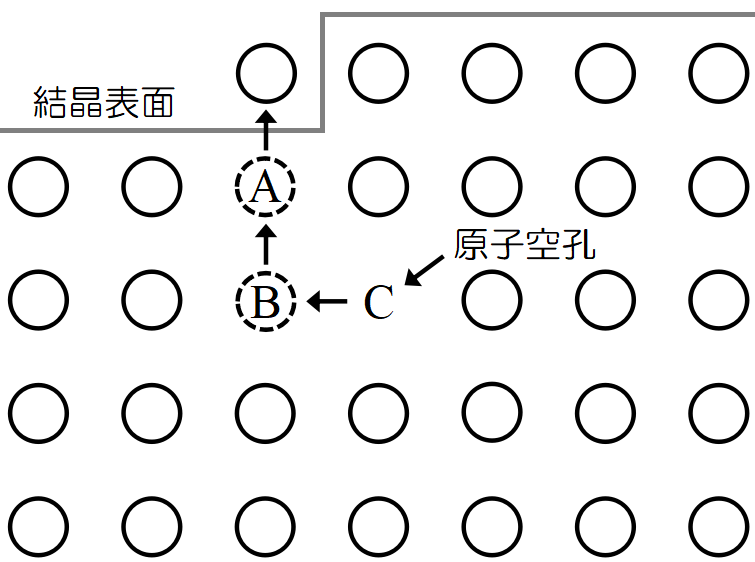
空孔形成の過程は種々あるが, 図の例が分かり易い。結晶表面にある原子\(~\rm A~\)が激しく振動して元の位置から抜け出す。次にそれによって生じたスペースを原子\(~\rm B~\)が埋め, さらに原子\(~\rm B~\)のスペースを原子\(~\rm C~\)が埋めて, 原子\(~\rm C~\)の位置が原子空孔となる。空孔が結晶内を移動すると考えても良い。このプロセスが概ね正しい事は次の様にして分かる。
結晶中にある1原子が, その周りを\(~Z~\)個の原子で取り囲まれているとする。原子間結合がこれらの\(~Z~\)個の最近接の配位原子のみによって与えられると仮定すると, 原子を取り去るエネルギーは
\[E_{remove}=Z\varepsilon_b \]
で与えられる。ここで\(~\varepsilon_b~\)は個々の原子間の結合手の結合エネルギーである。次に, 取り去った原子を表面に置くと, 表面の原子と結合することになる。
結晶内から取り除かれた原子が表面に置かれ新たな表面を形成するとすれば, その原子の結合手は表面の法線方向だけが繋がっていないので, 結合は3分の2になり結合した分だけ, すなわち
\[E_{surface}\simeq\frac{2Z}{3}\varepsilon_b \]
だけエネルギーが低下する。これより空孔を作るエネルギーは概ね
\[E_V=E_{remove}-E_{surface}=\frac{Z\varepsilon_b}{3} \]
となる。ここで固相から直接気相に変化する昇華\(~(sublimation)~\)のエネルギーを\(E_{sub}~\)とすると, これは結晶を構成する原子間の結合手を全て切るために必要なエネルギーであるから,
\[E_{sub}=Z\varepsilon_b \]
である。よって,
\[E_V=\frac{E_{sub}}{3}\tag{2} \]
とおおよその値が得られる。
実際には, もう少し複雑であるが, 銅\(~(Cu)~\)の場合, 昇華熱\(~3.54(eV)~\)(理論値)を3で割れば\(~1.18(eV)~\)となり, 空孔形成エネルギー\(~1.17(eV)~\)(実験値)と良い一致を示す。
上記の説明では空孔を介して原子が移動するのに必要なエネルギー(空孔移動エネルギーと呼ぶ.)が抜けている。(2)式が実測値と良い一致を示すという事は, 空孔移動エネルギーは空孔生成エネルギーと比べてかなり低い事を示唆している。
空孔が移動するには隣の原子の振動エネルギーに打ち勝つ必要がある。空孔移動エネルギー\(~(E_{move})~\)を格子点の原子の振動エネルギーと同程度と考えれば,
\[E_{move}\simeq k_BT \]
程度であろう。
原子空孔の熱平衡濃度 教科書の定番
格子点が\(N~\)個の金属結晶を考え, そのうち\(~n~\)個が空孔になっているものとする。
空孔がゼロの完全結晶が最も内部エネルギーが低い凝縮状態である。空孔ができると内部エネルギーは
\[\varDelta U=nE_V\tag{3} \]
だけ増加する。
次にエントロピーの変化を見よう。空孔が存在すると, 空孔を格子に配置する方法の多様性が配置のエントロピーを与える。\(~n~\)個の空孔を\(~N~\)個の格子点に配置する『場合の数』は,
\[W={}_NC_n=\frac{N!}{(N-n)!\;n!}\tag{4} \]
である。ボルツマンの原理(関係式)により, 空孔の配置によるエントロピーの変化\(~\varDelta S_C~\) は
\[\varDelta S_C=k_BlogW=k_B[NlogN-(N-n)log(N-n)-nlog\;n]\]
で与えられる。スターリングの近似式, \(N\gg 1~\)の時\(~logN!=NlogN-N~\)を用いた。
\(S_C~\)は混合エントロピーまたは配置\(~(configration)~\)のエントロピーと呼ばれる。後者のほうが一般的な様である。
また空孔が生成されたことにより, 空孔の周囲の熱振動が変化し, エントロピーの変化をもたらす。空孔1つ当たりのこのエントロピー変化を\(~S'~\)とすると, 結局エントロピーの変化は,
\[\varDelta S_C=k_B[NlogN-(N-n)log(N-n)-nlog\;n]+nS'\tag{5} \]
となる。\(S'~\)は振動エントロピー, または欠陥生成エントロピーと呼ぶ。
ここで
\(~U=U(S,V)~\)平衡曲面上の状態点\(~(U_0,S_0,V_0)~\)における接平面が示す値のうち, \(F_0=U_0-T_0S_0~\)に注目する。
本来は\(~G_0~\)の方が適切であるが, \(F_0~\)の方が解析が容易であり, また\(~G_0~\)との差は大きくない。
(3), (5)式より
\[\varDelta F=\varDelta U-T\varDelta S=nE_V-k_BT[NlogN-(N-n)log(N-n)-nlog\;n]-nTS'\tag{6}\]
が得られる。注意点を挙げておく。\(N\gg n~\)だから, 上式で
\[NlogN-(N-n)log(N-n)-nlog\;n=-nlog\;n\tag{7} \]
と近似すると, 空孔濃度\(~n/N~\)が求められなくなる。また, その近辺での精度も劣るので,
\[NlogN-(N-n)log(N-n)-nlog\;n=nlogN-nlog\;n \]
とした方が良い。(7)式で筆算をして随分時間を無駄にした。
ここで例として銅\(~(\rm Cu)~\)原子を考える。次の値を用いた。\(N=8.5\x 10^{22}/cm^3,\;E_V=1.17\,(eV),\;S'/k_B=1.5\)。
\(N~\)以外はデータも少なく(多くは1960年代の測定), またばらつきも大きいので, ある程度, 定性的な議論になるのは止むを得ない。
\(k_B=1.341\x 10^{-23}(J/\mathrm{^\circ K})~\)を用いると, \(k_BT_{300}=2.51\x 10^{-2}(eV)\), \(k_BT_{1356}=1.13\x 10^{-1}(eV)\), \(T_{300}S'=0.04(eV),\;T_{1356}S'=0.17(eV)~\)程度となる。\(TS'~\)の項は, \(E_V=1.17(eV)~\)と比べて小さいので省略しても大差は無いが, 本記事ではそのまま用いている。\(1356\mathrm{^\circ K}~\)は銅\(~(\rm Cu)~\)の融点である。
因みに\(~N~\)は, 銅\(~(\rm Cu)~\)の原子量\(~63.546~\), 比重\(~8.94g/cm^3~\)より, 単位体積当たりの原子数は,
\[N=6.02\x 10^{23}\x \frac{8.94}{63.546}=8.5\x 10^{22}/cm^3 \]
と算出される。色々調べている時に, T大と並ぶ某有名大学の演習問題になっているのを見つけた。高校一年生程度と思うが。
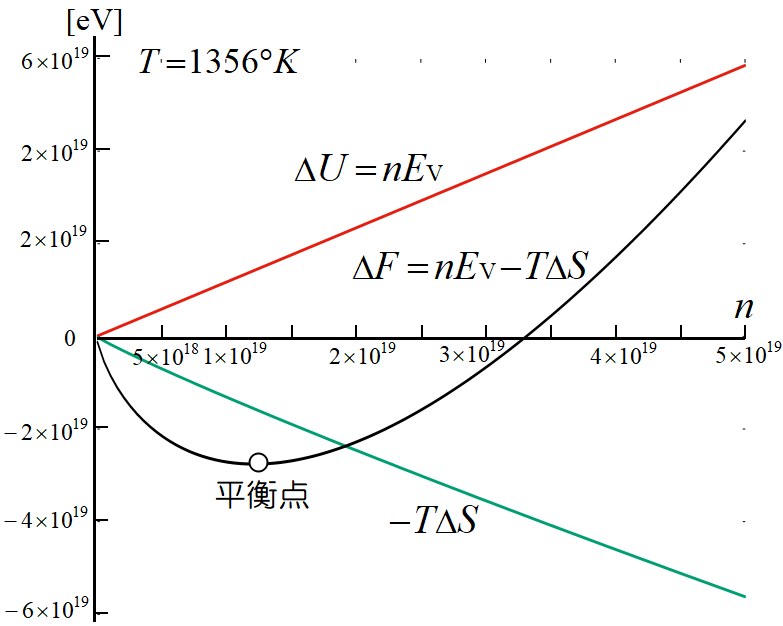
これらの値を用いて(3), (5), (6)を図示すると, \(1cm^3~\)の銅\(~(\rm Cu)~\)原子の空孔について次図を得る。
すぐ下の説明(8)式で分かるように, 平衡点の空孔濃度は\(1.43\x 10^{-4}~\)なので, 空孔数は\(~N=8.5\x 10^{22}~\)をかけて, \(~n=1.22\x 10^{19}~\)個となる。
\(\varDelta F~\)は20倍に拡大してある。計算値は赤線と緑線の間に収まっている。
図では緑色の\(-T\varDelta S~\)も直線に見えるが, 僅かに下に凸の曲線である。計算ソフトは精確で, 定規を当ててみると分かる。
\(\varDelta U~\)と\(~T\varDelta S~\)は拮抗しており, その差である\(\varDelta F~\)は小さな値を取る。
ギブスの平衡曲面によれば, 系が\(~T,\;p~\)が一定の多相平衡状態にあれば, \(G\equiv U-TS+pV,\;F\equiv U-TS,\;H\equiv U+pV~\)等の値が一定となる。
上図で平衡点と記した点である。
この点はまた, \(\partial \varDelta F/\partial n=0~\)から計算出来て,
\[\dd{\varDelta F}{n}=E_V-TS'-k_BTlog(n/N)=0 \]
より
\[C_V=\frac{n}{N}=exp\left(\frac{S'}{k_B}\right)exp\left(\frac{-E_V}{k_BT}\right)\tag{8} \]
を得る。\(C_V~\)は\(~F~\)が極小, ギブスの表現では\(\varDelta F~\)が一定となる点を与える空孔の濃度である。
多くの教科書, ネット記事では\(~\partial \varDelta F/\partial n=0~\)を当然の如くに扱うが, その正当性は, 化学ポテンシャルを含む多くの試行錯誤の結果得られたものである。当初は理由は分からないが平衡点で\(~G,F~\)等が一定の値を保つというのが正しい解釈と思う。
因みに\(~300\rm{^\circ}K,\;1356\rm{^\circ}K~\)における空孔濃度は, \(E_V=1.17\,(eV),\;S'/k_B=1.5~\)を用いると,
\[C_{V_{300}}=2.55\x 10^{-20},\;C_{V_{1356}}=1.43\x 10^{-4} \]
である。他の金属でも融点近くの空孔濃度は\(~\sim 10^{-4}~\)であることが分かっている。
前掲の, 銅\(~(\rm Cu)~\)における結晶欠陥数\(~n~\)と\(~\varDelta U,\;-TS,\;\varDelta F~\)の関係図は, \(~\varDelta F~\)を拡大していることもあって分かり難い。(拡大しないと極小点が殆ど見えず, 更に分かり難い。筆者も探し当てるのに苦労した.)。
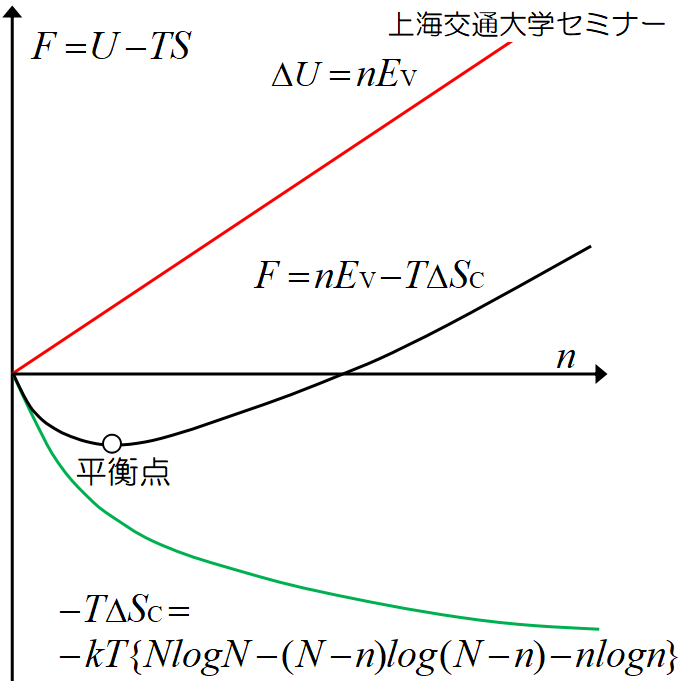
一方, 下図は様々な文献で引用される結晶欠陥のエネルギー図であり, 遥かに分かり易い。筆者は作成方法が分からず, 時間を無駄にしただけであったが, 説明には便利なのでこの図を引用させて頂く。
\(F=U-TS=nE_V-kT_BlogW~\)が極小値を持つのは, \(n~\)が平衡濃度に達するまでは, \(logW~\)が直線より急激に変化するのが原因である。
絶妙な自然の配慮と言えなくもない。
\(\rm TS~\)項の意味 不自由エネルギーの正体は?
ある温度\(~\rm T~\)で, 原子空孔が\(~n~\)個あったとする。
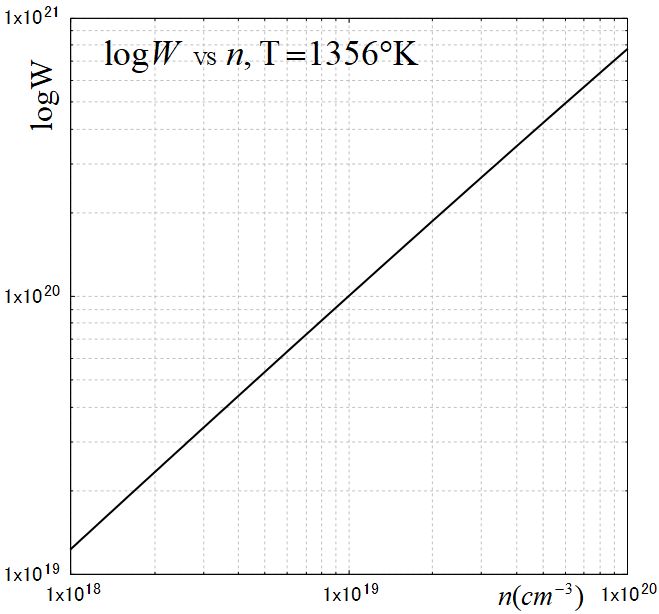
図は空孔数\(~n~\)と空孔の配置の組み合わせの対数, \(logW=NlogN-(N-n)log(N-n)-nlog\;n~\)をプロットしたものである。直線の様に見えるがわずかに上に凸の曲線である。
例えば平衡濃度に近い\(~n=1\x 10^{19}(cm^{-3})~\)の時, \(logW\simeq 10^{20}\)であるから, \(W\simeq exp(10^{20})~\)で天文学的な配置数になる。平衡状態ではこの天文学的な組み合わせのうちの何通りかの配置を行き来し, その時\(~k_BT~\)程度のエネルギーが使われる。
因みに配置換えに要する時間を\(~1\x 10^{-12}sec=1psec~\)とすると, この配置数を全て実現するのに要する時間は\(~exp(10^{21})\x 10^{-12}sec~\)であるが, 筆者のソフトでは計算不能であった。\(~exp(10^{2})\x 10^{-12}~\)でも\(~2.69\x 10^{31}sec~\)で宇宙の年齢を遥かに超える。\(300^{\circ}\rm K~\)でも事情は同じである。
\(\rm TS~\)項の働き(1) 配置換えのエネルギー
先ず空孔を増加させる過程を考えて見よう。外界から熱(エンタルピー)を加えて\(~n~\)個の空孔を実現するには, 空孔形成エネルギー \(~nE_V~\)の他に空孔移動の\(~kT_B\x logW~\)程度のエネルギーが必要である。対数を取っているので, この表現は不正確である。本来は「エントロピー換算熱」とでも言わねばならないが, 「エントロピー」を使えば, また分からなくなる。他に良い表現が無いので, このまま使う。\(kT_B\x logW=TS~\)は空孔の配置が入れ替わる時に必要な「不本意なエネルギー」であり, 膨大な配置数のうちのいくつかを実現する時に使われる。
空孔が増加して結晶の内部エネルギーが増加すると, 空孔の配置替えに必要な「不本意なエネルギー」も増加し, 取出せるエネルギーもその分だけ減少する。内部エネルギーの増加\(~=~\)取出せるエネルギーの増加とはならない。
平衡濃度に至る段階では, 配置換えエネルギー\(~k_BTlogW=k_BT\{NlogN-(N-n)log(N-n)-nlog\;n\}~\)の変化の方が空孔形成エネルギー\(~nE_V~\)よりも大きい。つまり取出せるエネルギーが思うように増えないどころではなく, 内部エネルギーの増加よりも「不本意エネルギー」の増加の方が大きくなり, 却って取出せるエネルギーが減少してしまう。
ヘルムホルツの主張
「束縛エネルギーとは, 温度\(~T~\)において物体のエントロピー\(~S~\)を生み出すために物体に取り込まなければならない熱量の力学的等価量である.」, あるいは「エンタルピーとエントロピーのせめぎあい」とはこういう事である。
\(\rm TS~\)項の働き(2)
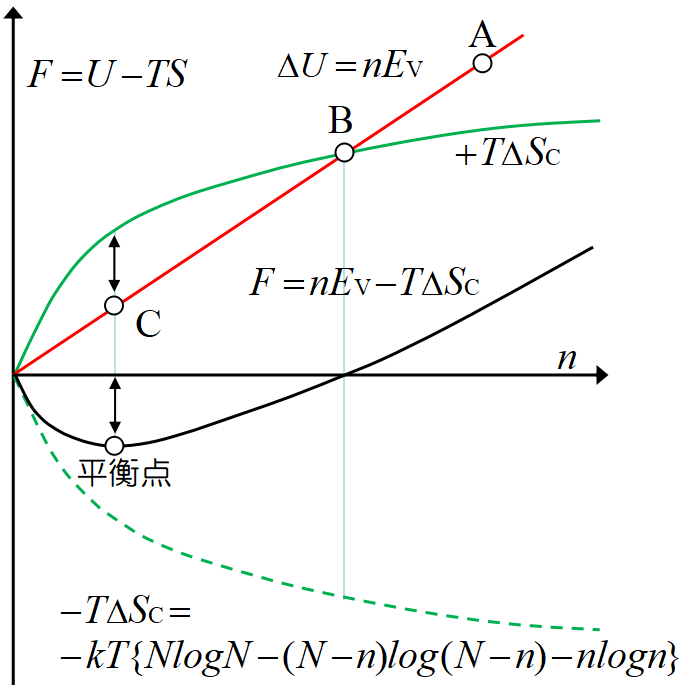
改めて下図を使って, 平衡点に至る過程を説明しよう。こちらの方が分かり易いかもしれない。
緑実線は\(~+T\varDelta S_C~\)であり, \(F=\varDelta U-T\varDelta S_C~\)は赤線と緑実線の差である。
物質が\(~\rm A~\)点にあったとしよう。内部エネルギーは減少しようとするので\(~\rm A\to B\to C~\)と変化する。図から明らかに赤線と緑実線の差は極小値を取った後 0 に向かう。
ヘルムホルツは全ての物理現象を「最小作用の原理」で説明しようとした。この試みは成功しなかったが, 電池の化学反応で, 実際に\(~F~\)の微分が電池の電圧を与え, また\(~F~\)の極小点で平衡反応を示すことから, ヘルムホルツは自信を持って\(F=U-TS~\)を
自由(ポテンシャル)エネルギーと命名したのであろう。現代では当然の如く\(~\partial F/\partial n=0~\)とするが。
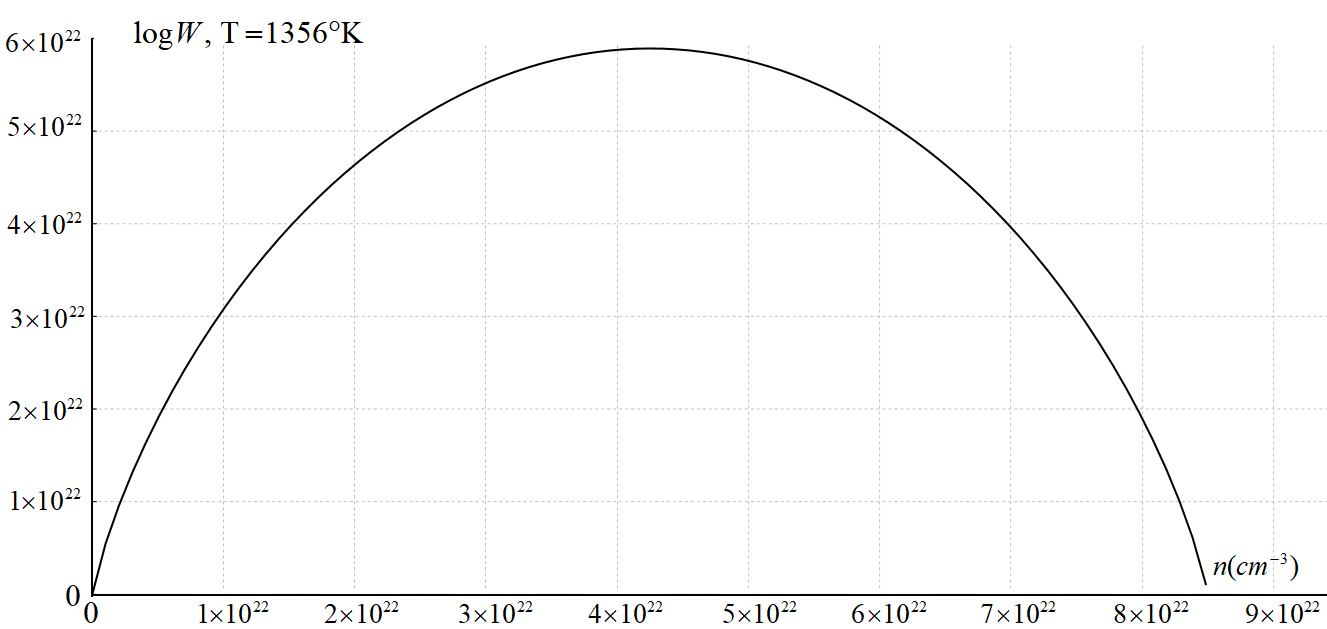
なお下図は空孔数\(~n~\)に対する\(~logW~\)である。\(n=N/2~\)の時\(~logW~\)が最大値を取る, すなわち\(~TS=k_BTlogW~\)が極大値を取るのが, \(F=U-TS~\)が極小値を持つ理由であると考えやすいが間違いである。\(logW(n)~\)と\(~n~\)の変化の仕方が, たまたま極小値を作り出しただけである。
余談 完全結晶
ウィスカー, ひげ結晶と呼ばれる無欠陥の金属もある。錆びやすい金属の代名詞である鉄のひげ結晶は全く錆びない。応力強さも通常の鉄の10倍もの強度を持つ。学生時代筆者も見た事があるが, 金(Gold)のようであった。少しひねって欠陥を入れるとたちまち錆びる。
積み木崩しの積み木は, 隙なくきっちり組めば高く積み上げられる。しかし10の23乗個もの積み木を完璧には組めない。ある割合で崩れた積み木が混じるのは止むを得ないし, そのほうが安定する。必要悪というところであろうか?