楽しく学ぶ…熱力学
熱力学関数(2) グリーンの定理
積分定理の王。粉ひき風車小屋で, 苦学の数学者ジョージ・グリーンによって与えられた。
線積分が積分経路に依らないための必要十分条件
前節において, ベクトル場の線積分が積分経路に依らない例を見た。結論を言ってしまおう。全微分
\[d'W=\Vec F(\bm{r})\cdot d\bm{r}=P(x,y)dx+Q(x,y)dy\tag{1} \]
に於いて,
\[\dd{P(x,y)}{y}=\dd{Q(x,y)}{x}\tag{2} \]
が成り立つ時, ベクトル場の線積分は経路に依らない。
例1 \(\Vec F(\bm{r})=(2y,3x)~\)の場合は積分経路に依って異なる値を取った。
\[d'W=\Vec F(\bm{r})\cdot d\bm{r}=2ydx+3xdy \]
で見てみると,
\[\dd{P}{y}=\dd{(2y)}{y}=2,\quad \dd{Q}{x}=\dd{(3x)}{x}=3 \]
で, (2)式の条件を満たしていない。
例2 \(\Vec F(\bm{r})=(2xy^3,3x^2y^2)~\)の場合は積分経路に依らず, 同じ値を取った。
\[d'W=\Vec F(\bm{r})\cdot d\bm{r}=2xy^3dx+3x^2y^2dy\tag{3} \]
で見てみると,
\[\dd{P(x,y)}{y}=\dd{(2xy^3)}{y}=6xy^2, \quad\dd{Q(x,y)}{x}=\dd{(3x^2y^2)}{x}=6xy^2 \]
であり,
\[\dd{P(x,y)}{y}=\dd{Q(x,y)}{x} \]
となり, 確かに(2)式の条件を満たしている。
更に\(~\Vec F(\bm{r})=(2xy^3,3x^2y^2)~\)では,
\[W(x,y)=x^2y^3\tag{4} \]
が得られ, 勾配\(~\nabla W(x,y)~\)を求めると,
\[\nabla W(x,y)=\left(\dd{W}{x},\dd{W}{y}\right)=(2xy^3,3x^2y^2) \]
すなわち,
\[\Vec F(\bm{r})=(-)\nabla W(\bm{r}) \]
となっている。
(3)式の右辺を 0 と置いた完全微分方程式
\[2xy^3dx+3x^2y^2dy=0 \]
の解は,
\[\Phi(x,y)=x^2y^3=C \]
であり, (4)式と一致していた。
全微分\(~d'W=P(x,y)dx+Q(x,y)dy~\)が
\(~\partial{P(x,y)}/\partial{y}=\partial{Q(x,y)}/\partial{x}~\)を満たすとき, この微分形式\(~d'W~\)を
完全微分(完全な全微分で完全全微分の方が自然な気がするが)と呼ぶ。
最早 '(ダッシュ)をつける必要はなく, \(d'W \to dW~\)として良い。全微分が完全微分になる。
完全微分\(~dW~\)は積分可能である。積分可能とは, 計算ができるだけではなく, 積分値が一つに確定する, という意味である。
適当な基準点\(~\bm{r}_0=(x_0,y_0)~\)を選んで,
\[W(\bm{r})=\int_{\bm{r_0}}^{\bm{r}}dW \]
で, 点\(~\bm{r}=(x,y)~\)の積分値を定義すれば, その値は経路に依らず, 一つに定まるという事である。
グリーンの定理
グリーンの定理は平面上の線積分を面積分に書き換えたり,その逆をするのに使われる。流体力学, 電磁気学等において不可欠であるばかりでなく, 純粋数学においても大変重要で, リーマンはグリーンの定理を基礎として, 複素関数の理論を構築した。変分法, 固有関数, 積分方程式など至る所でこの定理に出会う。なおこの記事は「平面のグリーンの定理」で, 他にガウスの発散定理から導かれるグリーンの定理があるので注意。
グリーンの定理証明 ベクトル解析の例はガウスの発散定理とストークスの回転定理を参照
証明すべき定理は以下の(5)式である。単純閉曲線\(~C~\)の周回線積分と, \(~C~\)の囲む領域\(~S~\)の2重積分が等しいことを表している。
\[\oint_CP(x,y)dx+Q(x,y)dy=\iint_S dxdy\left(\dd{Q(x,y)}{x}-\dd{P(x,y)}{y}\right)\tag{5} \]
(証明)
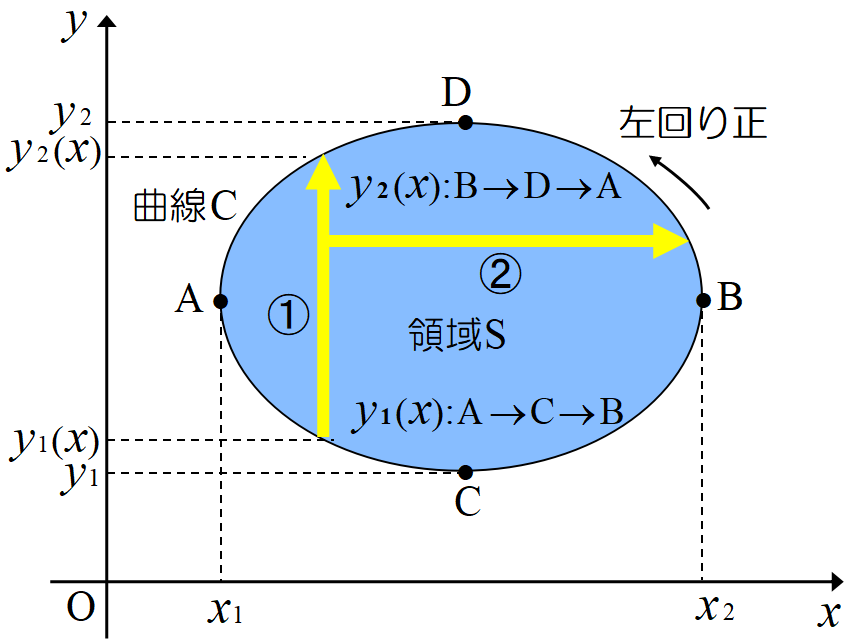
(5)式右辺, 領域\(~S~\)について, 第2項から積分を行う。①先ず\(x~\)を固定して\(~y~\)方向に積分した後, ②\(~x~\)方向に積分する。
\[\begin{align}
-\iint_S dxdy\dd{P(x,y)}{y}
=&-\int_{x_1}^{x_2}dx\int_{y_1(x)}^{y_2(x)}dy\dd{P(x,y)}{y} \\
=&-\int_{x_1}^{x_2}dx[P(x,y_2(x))-P(x,y_1(x))] \\
=&\int_{x_2}^{x_1}dxP(x,y_2(x))+\int_{x_1}^{x_2}dxP(x,y_1(x)) \\
=&\oint_C P(x,y)dx \tag{6}
\end{align}\]
1→2行目は\(~y~\)で微分して\(\left(\displaystyle \dd{}{y}\right)\), \(y~\)で積分\(~(dy)~\)するので, 不定積分は\(~P(x,y)~\)である。従って,
\[\int_{y_1(x)}^{y_2(x)}dy\dd{P(x,y)}{y}=\left[P(x,y)\right]^{y_2(x)}_{y_1(x)}=P(x,y_2(x))-P(x,y_1(x)) \]
2→3行目では, 第1項の積分の順序を変え, 符号を(ーから+へ)変えた。
(5)式右辺第1項も同様にして,
\[\begin{align}
\iint_R dxdy\dd{Q(x,y)}{x}
=&\int_{y_1}^{y_2}dy\int_{x_1(y)}^{x_2(y)}dx\dd{Q(x,y)}{x} \\
=&\int_{y_1}^{y_2}dy[Q(x_2(y),y)-Q(x_1(y),y)] \\
=&\int_{y_1}^{y_2}dyQ(x_2(y),y)+\int_{y_2}^{y_1}dyQ(x_1(y),y)) \\
=&\oint_C Q(x,y)dy \tag{7}
\end{align}\]
(6)式と(7)式の辺々を加えると, グリーンの定理(5)式が得られる。
より一般的な閉曲線の場合は, グリーンの定理で検索されたし。
線積分が積分経路に依らないための必要十分条件
さて(5)式グリーンの定理に於いて, \(~\partial{Q(x,y)}/\partial{x}=\partial{P(x,y)}/\partial{y}~\)の時, 右辺の被積分関数は 0(ゼロ) だから, 左辺の周回積分も 0 である。
周回積分が 0(ゼロ)の時, ポテンシャル関数\(~F(x,y)~\)が存在した。
改めて整理すると, \(~C^2~\)級の2変数関数(この熱力学では2変数関数に限ります)\(~F(x,y)~\)が存在して,
\[dF(x,y)=\dd{F(x,y)}{x}dx+\dd{F(x,y)}{y}dy=P(x,y)dx+Q(x,y)dy\tag{8} \]
と表したとき,
\[\dd{P(x,y)}{y}=\dd{Q(x,y)}{x}\tag{9} \]
ならば, \(F(x,y)~\)はポテンシャル関数で, 積分経路に依らない状態量を与える。
補足すると, (9)式が成り立つ時,
\(~dF=0~\)すなわち, \(F(x,y)=Const.~\)なる関数が存在し, \(F(x,y)~\)はポテンシャル関数となる。
次の説明の方が直接的である。"周回積分"という用語は出て来ない。
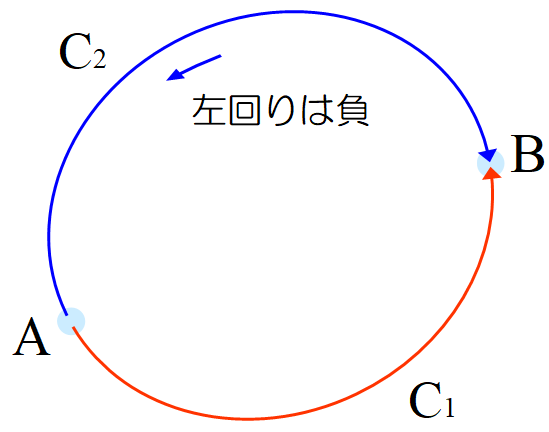
(5)式における左辺の周回積分を, 経路\(~C_1~\)と\(~C_2~\)上の線積分の和として表す。\(C_2~\)が\(~C_1~\)と逆向きであることを考慮して, (5)式は
\[\int_{C_1}P(x,y)dx+Q(x,y)dy-\int_{C_2}P(x,y)dx+Q(x,y)dy=\iint_S\left(\dd{Q(x,y)}{x}-\dd{P(x,y)}{y}\right) \]
と書ける。ここで\(~\partial{Q(x,y)}/\partial{x}=\partial{P(x,y)}/\partial{y}~\)ならば
\[\int_{C_1}P(x,y)dx+Q(x,y)dy=\int_{C_2}P(x,y)dx+Q(x,y)dy \]
\(C~\)が任意, すなわち\(~C_1,\;C_2~\)が任意の時, \(A\to B~\)の積分値\(~F(B)-F(A)~\)は経路に依らない状態量である。
つまり任意の関数が, その積分経路に依らず, 始点と終点のみに依るとは, 関数\(~F(x,y)~\)の全微分
\[dF=\dd{F(x,y)}{x}dx+\dd{F(x,y)}{y}dy \]
が完全微分になる事である。
グリーンの定理の幾何学的意味
\[\oint P(x,y)dx+Q(x,y)dy=\iint_S\left(\dd{Q(x,y)}{x}-\dd{P(x,y)}{y}\right)dxdy \]
において, \(P(x,y)=0,\;Q(x,y)=x~\)とおくと,
\[\oint xdy=\iint_S 1\cdot dxdy\tag{10} \]
今度は\(~P(x,y)=y,\;Q(x,y)=0~\)とおくと,
\[-\oint ydx=\iint_S 1\cdot dxdy\tag{11} \]
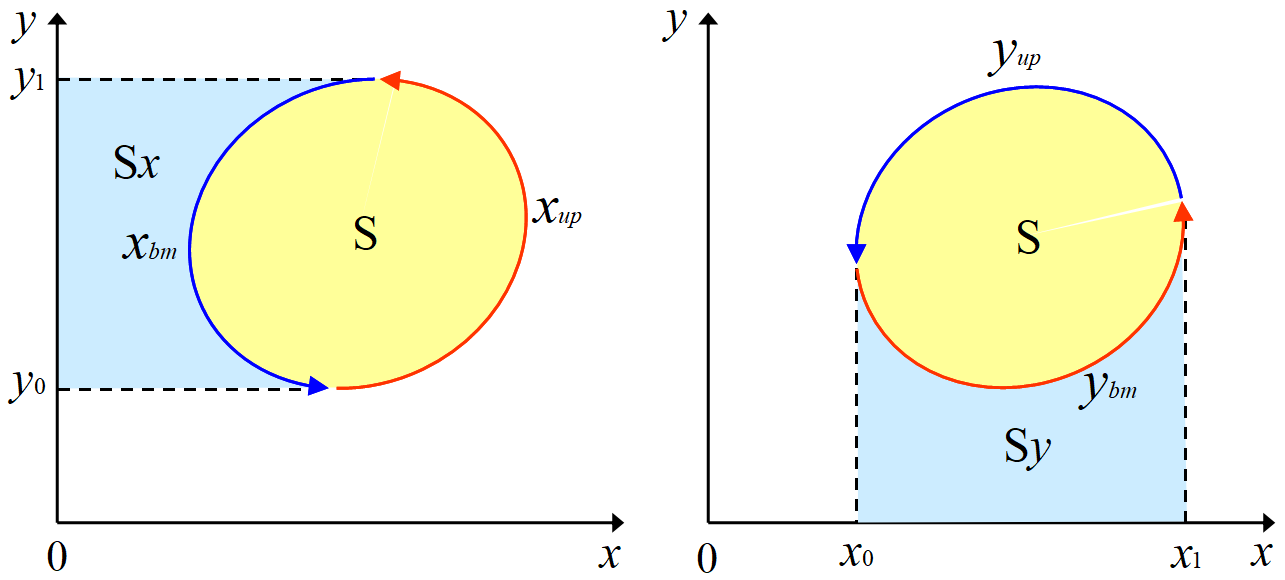
この2つの式の左辺の面積分は何れも図の面積\(~S~\)にとるものとする。
すると(10), (11)式左辺の線積分はそれぞれ,
\[\begin{align}
\oint_Cxdy&=\int_{y_0}^{y_1}x_{up}dy+\int_{y_1}^{y_0}x_{bm}dy \\
&=(S+S_x)+(-S)=S
\end{align}\]
および,
\[\begin{align}
-\oint_Cydx&=-\int_{x_0}^{x_1}y_{bm}dx-\int_{x_1}^{x_0}y_{up}dx \\
&=-S_y-(-S-S_y)=S
\end{align}\]
すなわち, 閉曲線\(~C~\)で囲まれた面積\(~S~\)を求める2通りの方法が
同じであることを示している。