|
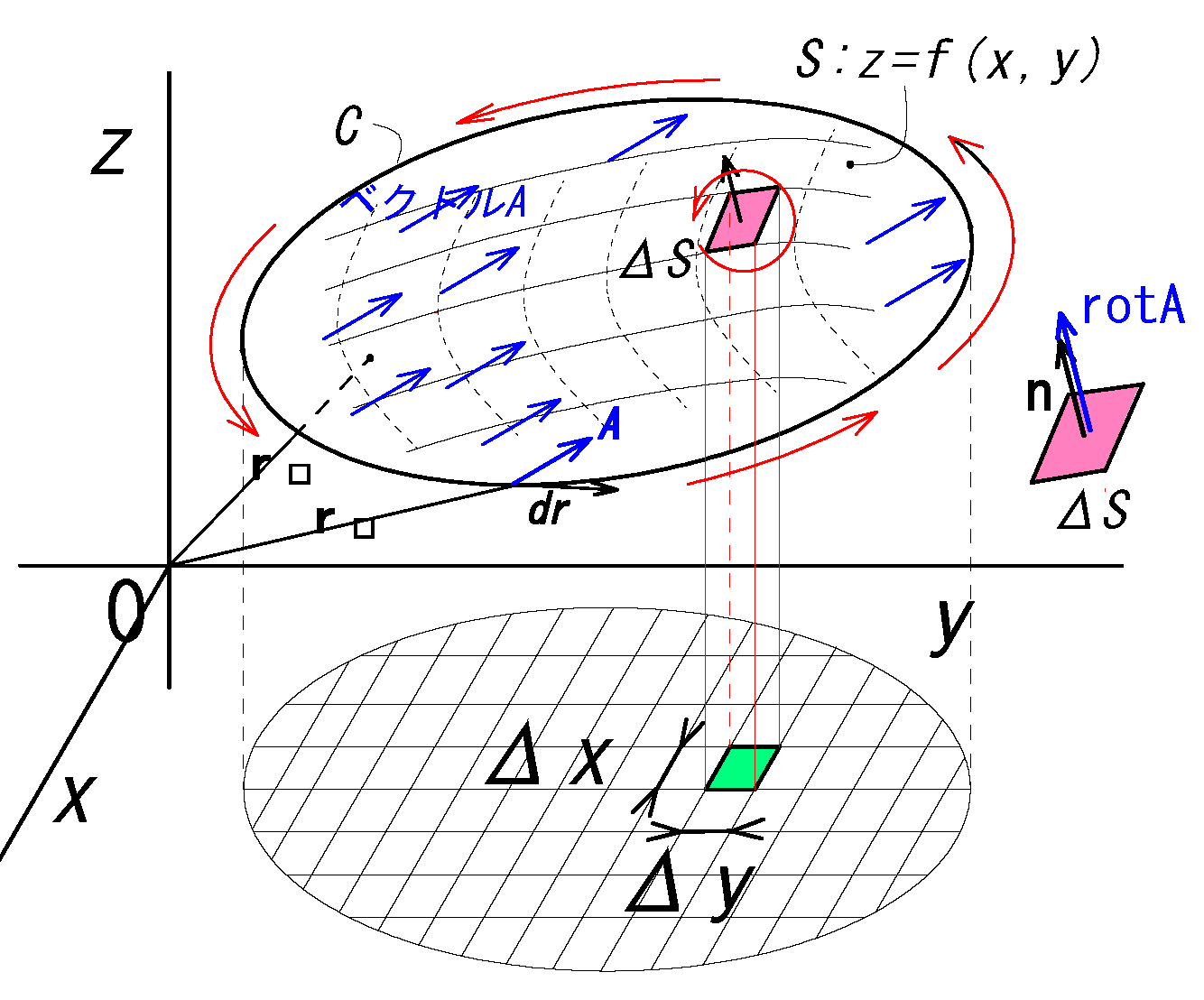
ストークスの定理
ベクトル場\(A(x,y,z)\)内におけるた単一閉曲線\(C\)、その平曲面上にある曲面を\(S\)とすると次式が成り立ちます。
\(\dsii_{S} (rot \bv{A}) \cdot \bv{n}dS \) \(=\displaystyle \oint_{C} \bv{A} \cdot \bv{u}dr\) \(=\displaystyle \oint_{C} \bv{A} \cdot d\bv{r}\) \(\quad ❶\) \(\bv{r}(x,y)\):曲面Sの位置ベクトル \(\bv{n}\):曲面Sの微小領域の単位法線ベクトル \(\bv{u}\):曲線Cの単位接線ベクトル |
\(rot\bv{A}=\left( \begin{array}{c} \pder{}{x}\\ \pder{}{y}\\ \pder{}{z} \end{array} \right) \) \( \x \) \( \left( \begin{array}{c} A_x \\ A_y \\ A_z \end{array} \right) \) \(= \left( \begin{array}{c} \pder{A_z}{y}-\pder{A_y}{z}\\ \pder{A_x}{z}-\pder{A_z}{x}\\ \ul{\pder{A_y}{x}-\pder{A_x}{y}} \end{array} \right) \)
2次元で考えると(上の縦行列の2行は0)\(\left( \begin{array}{c} \pder{}{x}\\ \pder{}{y}\\ \end{array} \right) \) \( \x \) \( \left( \begin{array}{c} A_x \\ A_y \\ \end{array} \right) \) \(= \left( \begin{array}{c} \ul{\pder{A_y}{x}-\pder{A_x}{y}} \end{array} \right) \)
これより
\( rot\bv{A}=\left(0,0,\pder{A_y}{x}-\pder{A_x}{y}\right) \)
\( \bv{n}=(0,0,1)\)
\( rot\bv{A}\cdot\bv{n}\)\(=(0,0,\pder{A_y}{x}-\pder{A_x}{y})\cdot(0,0,1)\)
\(=(0,0,\pder{A_y}{x}-\pder{A_x}{y})\)
\(\therefore\ \ul{rot \bv{A} \cdot \bv{n}}\ dS\)\(\simeq \ul{(\pder{A_y}{x} - \pder{A_x}{y})}\ ΔS \)
\(ΔS=ΔxΔy\) だから
\(Δx, Δy \to 0 \) にすると \(dS=dxdy\) となる。
これより
左辺
\(ⓐ=\dsii_{S} (rot \bv{A}) \cdot \bv{n}\ dS \)
\(=\dsii_{S} (\pder{A_y}{x}-\pder{A_x}{y})\ dxdy\)
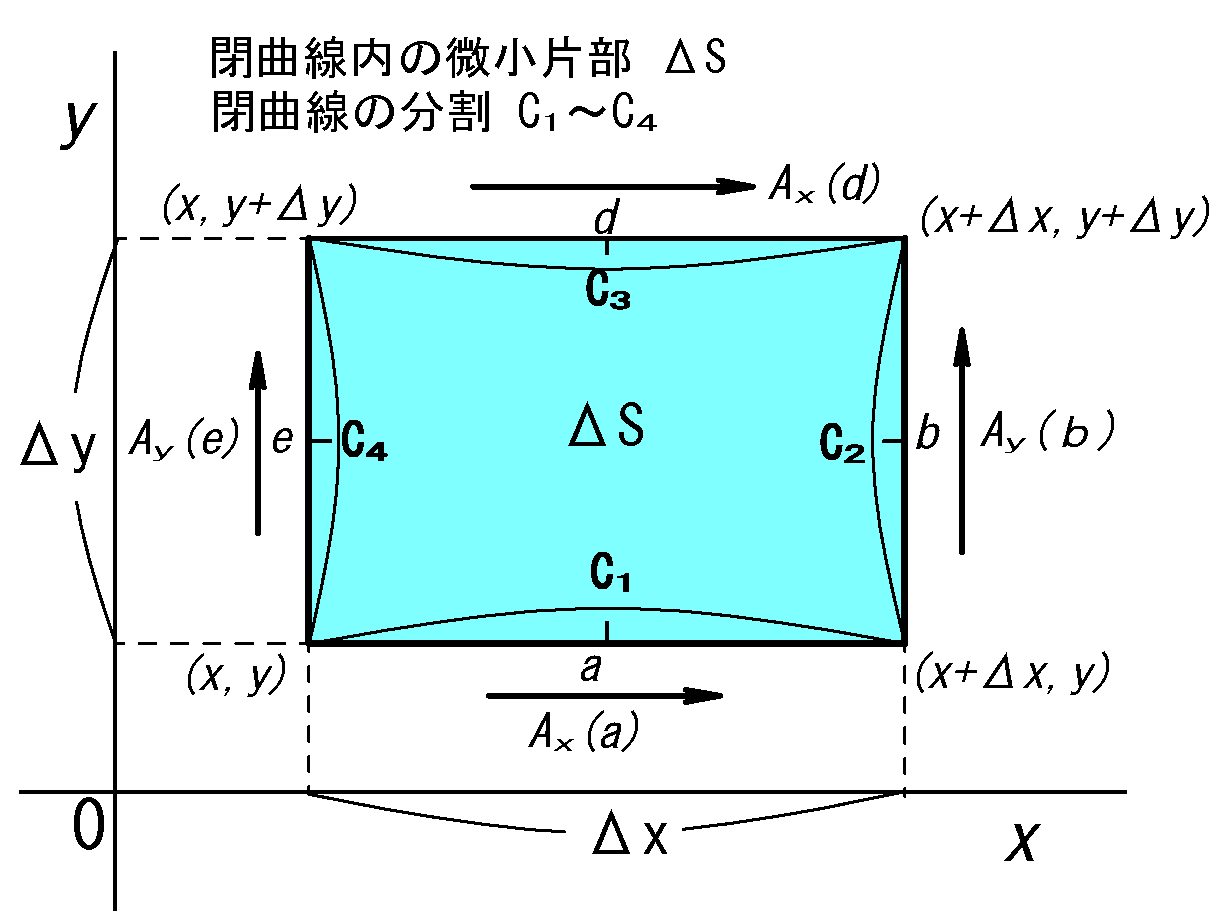
\( \displaystyle \oint_{C_j} \bv{A}\cdot d\bv{r}\) \(=\color{blue}{\dsi_{c_1} \bv{A}\cdot d\bv{r}}\) \(+\color{red}{\dsi_{c_2} \bv{A}\cdot d\bv{r}}\) \(+\color{blue}{\dsi_{c_3} \bv{A}\cdot d\bv{r}}\) \(+\color{red}{\dsi_{c_4} \bv{A}\cdot d\bv{r}}\)
積分領域が長方形、また線積分だから積分記号を外した次式で書ける。\(=\color{blue}{\bv{A_x}(a)\cdot \bv{C}_1}\)\(+\color{red}{\bv{A_y}(b)\cdot \bv{C}_2}\) \(+\color{blue}{\bv{A_x}(d)\cdot \bv{C}_3}\) \(+\color{red}{\bv{A_y}(e)\cdot \bv{C}_4}\)
\(\bv{C}_1= (x+Δx-x,y-y)=(Δx,0)\)
\(\bv{C}_2= (x+Δx-(x+Δx),y+Δy-y)=(0,Δy)\)
\(\bv{C}_3= (x-(x+Δx),y+Δy-(y+Δy))\) \(=(-Δx,0)=-(Δx,0)\)
\(\bv{C}_4= (x-x,y-(y+Δy))\) \(=(0,-Δy)=-(0,Δy)\)
\(a=(x+\frac{Δx}{2},y)\) \(\ ,\ \) \(b=(x+Δx,y+\frac{Δy}{2})\)
\(d=(x+\frac{Δx}{2},y+Δy)\) \(\ ,\ \) \(e=(x,y+\frac{Δy}{2})\)
\(\color{blue}{\bv{A_x}(a)\cdot \bv{C}_1}\)\(+\color{blue}{\bv{A_x}(d)\cdot \bv{C}_3}\)
\(= \bv{A_x}(x+\frac{Δx}{2},y)\cdot (Δx,0)\)\(+\bv{A_x}(x+\frac{Δx}{2},y+Δy)\cdot (-Δx,0)\)
\(= \bv{A_x}(x+\frac{Δx}{2},y)Δx\)\(-\bv{A_x}(x+\frac{Δx}{2},y+Δy)Δx\)
\(= \{\bv{A_x}(x+\frac{Δx}{2},y)\) \(-\bv{A_x}(x+\frac{Δx}{2},y+Δy)\}Δx\)
\(= \ul{ - \dsfr{ [\bv{A_x}(x+\frac{Δx}{2},y+Δy)-\bv{A_x}(x+\frac{Δx}{2},y) ] } {Δy} }ΔxΔy\)
\(\color{blue}{\bv{A_x}(a)\cdot \bv{C}_1}\)\(+\color{blue}{\bv{A_x}(d)\cdot \bv{C}_3}\) \(=\ul{-\color{blue}{\pder{\bv{A}_x}{y} } ΔxΔy}\)\(:(1)\)
上式は\(\bv{A_x}\)についての周回積分です。\(\color{red}{\bv{A_y}(b)\cdot \bv{C}_2}\)\(+\color{red}{\bv{A_y}(e)\cdot \bv{C}_4}\) \(=\color{red}{\pder{\bv{A}_y}{x}ΔxΔy}\)\(:(2)\)
(1),(2)より\(\therefore\) \(\displaystyle \oint_{\color{red}{C_j}} \bv{A} \cdot d\bv{r}\) \(=\color{red}{\pder{\bv{A}_y}{x}ΔxΔy}\)\(-\color{blue}{\pder{\bv{A}_x}{y}ΔxΔy}\) \(=(\pder{\bv{A}_y}{x}-\pder{\bv{A}_x}{y})dxdy\)
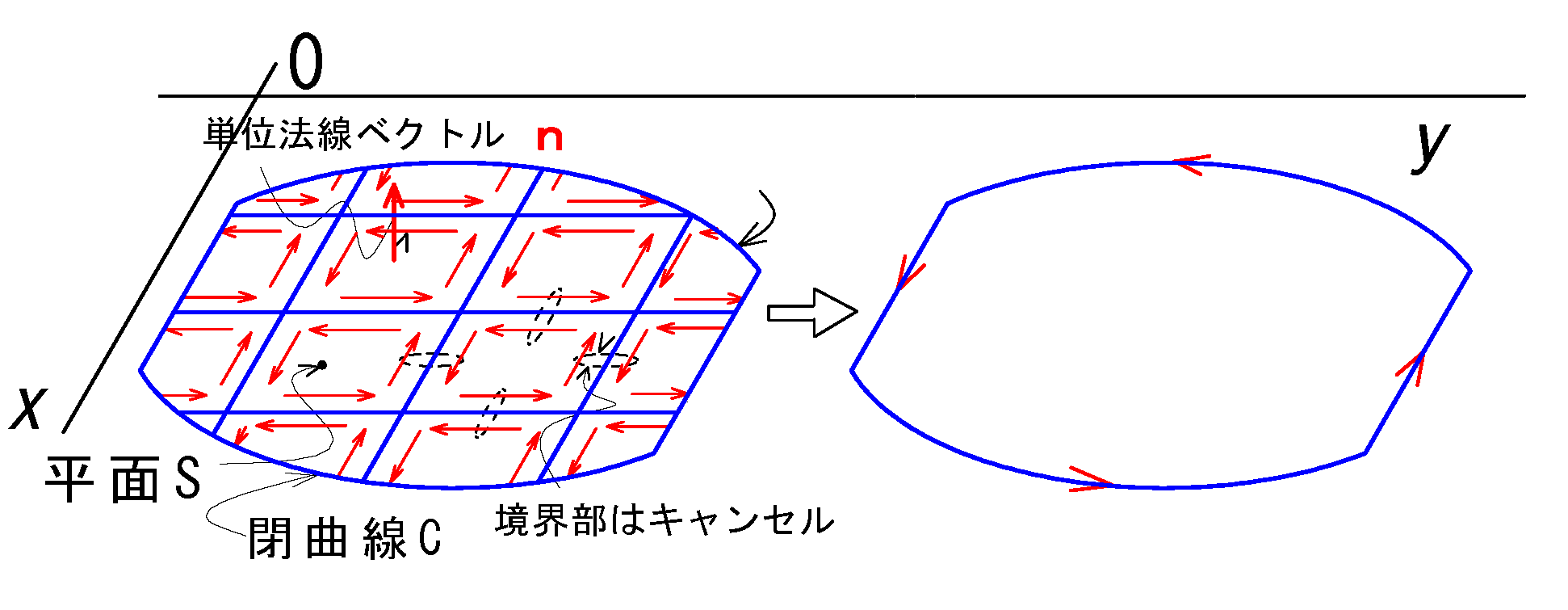
上記は微小片\(C_j\)における周回積分であり、曲面全体の閉曲線\(C\) における周回積分の総和は
積分領域\(C_j\)\(\to\)\(C\)にして
右辺
\(ⓑ=\displaystyle \oint_{\color{red}{C}} \bv{A} \cdot d\bv{r}\)
\(=\dsii_{S} (\pder{\bv{A}_y}{x}-\pder{\bv{A}_x}{y})dxdy\)
\(\bv{r}=(r_x,r_y,r_z)\)として:
\(\bv{n}=\dsfr{∇ r }{|∇ r|}\)
\(∇ r=(\pder{r_x}{x},\pder{r_y}{y},\pder{r_z}{z})\)
\(|∇ r|=\sqrt{(\pder{r_x}{x})^2+(\pder{r_y}{y})^2+(\pder{r_z}{z})^2}\)
\(\dsii_{S} (rot \bv{A}) \cdot \bv{n}dS \)
\(=\displaystyle \oint_{C} \bv{A} \cdot d\bv{r}\)
\(\ \scriptsize {:❶}\)
\(=\left( \begin{array}{c} \pder{}{x}\\ \pder{}{y}\\ \pder{}{z}\\ \end{array} \right) \) \( \x \) \( \left( \begin{array}{c} -y \\ x \\ 0 \\ \end{array} \right) \) \(= \left( \begin{array}{c} \pder{x}{x}-\pder{y}{y}\\ 0\\ 0 \end{array} \right) \) \(=(0,0,1-(-1))\)\(=(0,0,2)\)
☞ ベクトルの方向余弦 【参照先】
「面素・面素ベクトル」の❷-3,❼-1を用いて
\(\bv{n}=(cosα,cosβ,cosγ)\) \(\ \scriptsize {:❼-1}\)
\(dS=\dsfr{1}{|cosα|}yz\)\(=\dsfr{1}{|cosβ|}zx\)\(=\dsfr{1}{|cosγ|}xy\)
\(\ \scriptsize {:❼-1}\)
\(α,β=\frac{1}{2}\pi,\ γ=0\)
\(dS=\frac{1}{cos γ}dxdy\)\(,\ \) \(γ=0\)(∵円板)
\(dS=dxdy\)
極座標変換する----
\(dxdy=Jdrdθ=rdrdθ\)
ヤコビアン \(J=r\)
閉曲線\(C:x^2+y^2=4\)(半径2の円) より x,yをtで表すと:
\(\ x=2cost\) \(, \) \(\frac{dx}{dt}=-2sint\)
\(\ y=2sint\) \(, \) \(\frac {dy}{dt}=2cost\)
\(∇r=(\pder{r_x}{x},\pder{r_y}{y},\pder{r_z}{z})\)
\(=(2x,2y,2z)\)
\(|∇ r|=\sqrt{(\pder{r_x}{x})^2+(\pder{r_y}{y})^2+(\pder{r_z}{z})^2}\)
\(=\sqrt{(2x)^2+(2y)^2+(z)^2}\)
\(=\sqrt{4(x^2+y^2+z^2)}\)
\(=2\sqrt{x^2+y^2+z^2}\)
\(=2\sqrt{4}=4\)
\(dS=\frac{1}{cos γ}dxdy\)\(,\ \) \( cosγ=\dsfr{z}{2}\) \((∵上記ⓐ)\)
\(dS=\dsfr{2}{z}dxdy\)
\(=\dsii_{M} 2 rdrdθ\) \(=2 \dsi_0^{2\pi} \dsi_0^{2} \ r\ dr\ dθ \) \(=2 \dsi_0^{2\pi} \left[\dsfr{1}{2}r^2\right]_0^2 \ dθ \) \(=2 \dsi_0^{2\pi} \ 2 dθ \) \( = 2 \left[ 2 θ \right]_0^{2\pi}\) \(=2 \cdot 4 \pi=8\pi\)
\(\therefore \dsii_{S} (rot \bv{A}) \cdot \bv{n}dS=8\pi \)
\(\dsii_{S} (rot \bv{A}) \cdot \bv{n}dS \)
\(=\displaystyle \oint_{C} \bv{A} \cdot d\bv{r}\)
\(\ \scriptsize {:❶}\)

・\(\bv{E}\):電場\(\small{(N/C)}\) ・\(V\):電位\(\small{(V)=(J/C)}\)
・\(\bv{B}\):磁場\(\small{(Wb/m^2)}\)(磁束密度)
・\(\Phi\):磁束\(\small{(Wb)}\) ・\(ds\):積分の面要素
・\(S\):積分の閉曲面領域
・\(∂S\):積分の閉曲線(=C) (ここでの∂記号は「境界」を表している)
・\(n\):面要素\(dS\)の単位法線ベクトル
・\(x\):距離 \(\small{(m)}\)
・\(\oint_{C}=\oint_{∂S} \):周回積分
\(\dsii_{S}\ ( \color{blue}{∇\x \bv{E}+\pder{\bv{B}}{t} }) \cdot \bv{n}dS =0\) \(\ :②'\)
\(\qquad \qquad \quad \Downarrow \)
\( \underbrace{ \dsii_{S}\ ∇\x \bv{E} \cdot \bv{n}dS}_{Ⓐ}\)
\(= \underbrace{ \dsii_{S}\ -\pder{\bv{B}}{t} \cdot \bv{n}dS}_{Ⓑ}\)
\(Ⓐ\to \dsii_{S}\ ∇\x \bv{E} \cdot \bv{n}dS\)
\(=\displaystyle \oint_{C} \bv{E} \cdot d\bv{r}\)
左辺が式Ⓐとかけることがストークスの定理の応用です。
\(Ⓑ\to \dsii_{S}\ -\pder{\bv{B}}{t} \cdot \bv{n}dS\)
\(=-\dsfr{d}{dt} \dsii_{S} \bv{B} \cdot \bv{n}dS\)
(真中の式)「曲面Sを貫く磁束の時間的変化」と(左辺) その曲面の縁と交わる「閉曲線Cに沿った電場Eの総和(起電力)」に等しい。
物理的に言うと:(右辺)「閉回路を貫く磁束の変化速度」と(左辺)「閉回路に生じる起電力」の関係式である。
以下は一般のファラデーの電磁誘導の式です。