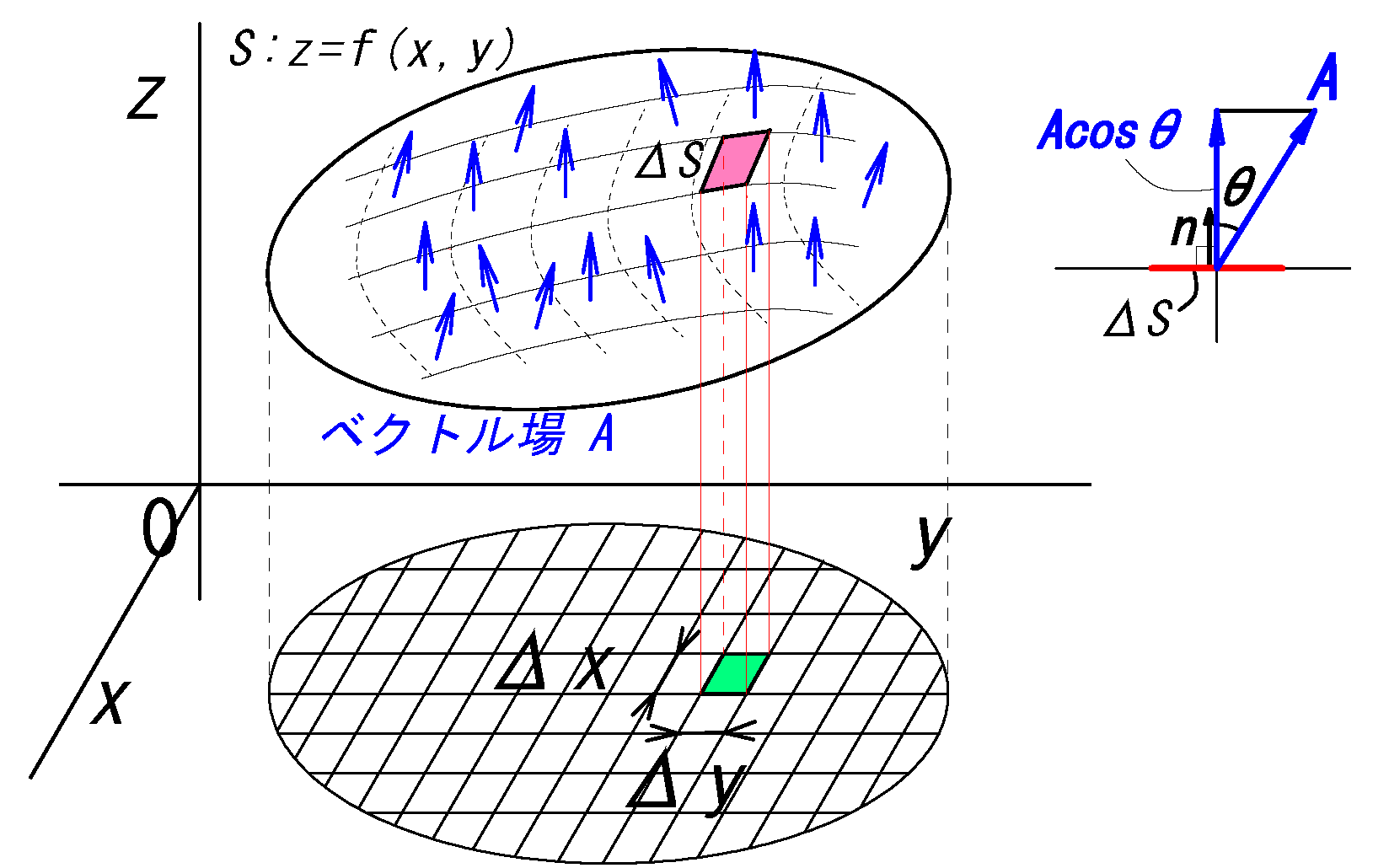
物理数学・ベクトル場の面積分|湘南理工学舎

導出の手順として被積分項を次の➀ と➁ に分けて導出していく。

\(　\iint_S \ \underbrace{\ \b{A}\cdot\b{n}\ }_{➀} \underbrace{\ dS\ }_{➁}\)

\(ｄｓ\) (➁ ) の導出

表記の簡素化のため、ここでは\(x_{+\Delta},y_{+\Delta y}\) を次のように表す。
\(\color{red}{ x_{+\Delta} }=x+\Delta x\) \(,\ \)\(\color{red}{ y_{+Δ} }=y+\Delta y\)
ベクトル\(\b{B},\b{C}\)は：

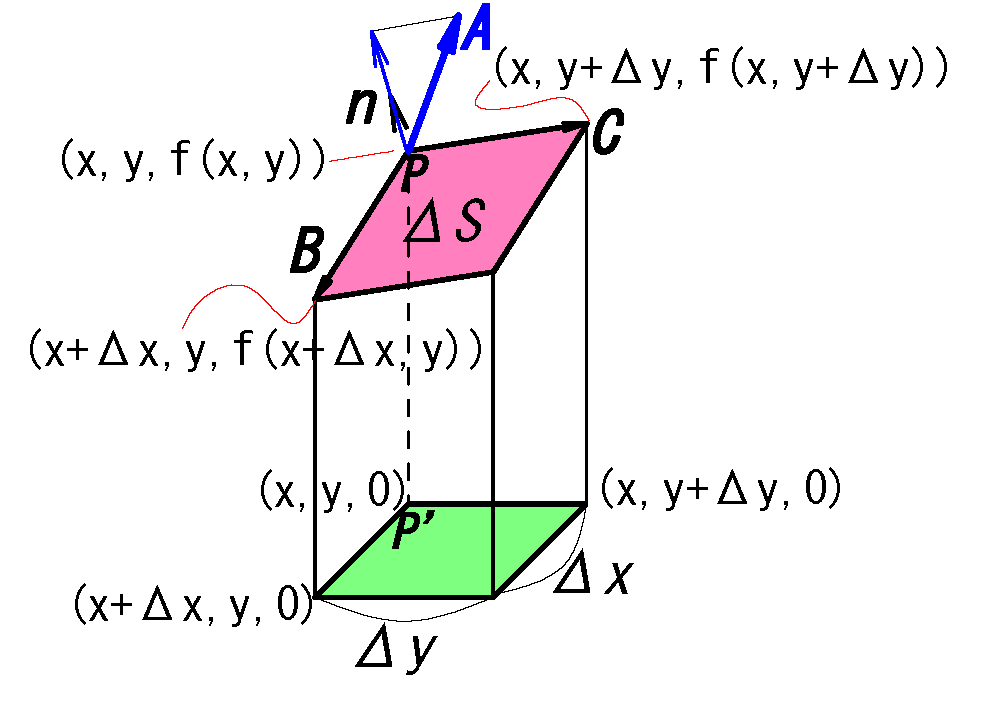
fig2 からベクトルの成分を求める（＝終点-始点）
例：\(\b{B}\)\(=(x_{+\Delta}-x,\ y-y,\ f(x_{+\Delta},y)-f(x,y))\)

\(\b{B}=( Δ x,\ 0,\ f(x_{+Δ},\ y)-f(x,y))\)
\(\b{C}=( 0,\ Δ y,\ f(x,\ y_{+Δ})-f(x,y))\)

ベクトル積（外積、クロス積）についてワンポイント：
・ベクトル積の大きさ（絶対値）\(|\color{red}{ \b{B} \x \b{C} }|\) は\(ΔS\) の面積を表します。
・ベクトル積 \(\color{red}{ \b{B} \x \b{C} }\) の結果(ベクトル)は、\(ΔS\)に垂直、すなわち法線ベクトルです。但し単位法線ベクトルではありません。
・単位法線ベクトルを求める式：　 \(\displaystyle \frac{\b{B} \x \b{C}}{|\b{B} \x \b{C}|}\)
・ベクトルの大きさは絶対値で表し、3平方の定理により計算（各成分の2乗の和の平方根）

上記を参考にして、ベクトルを以下のように縦行列に表示するとベクトル積の計算しやすい

\(\bv{B} \x \bv{C}\) \(=\left( \begin{array}{c} 　　Δ x　　\\ 　 0 \\ f(x_{+Δ},\ y)-f(x,y) 　　\end{array} \right) \) \( \x \) \( \left( \begin{array}{c} 0 \\ Δ y \\ f(x, y_{+Δ})-f(x,y) \end{array} \right) \)
☞ 上記のベクトル積の計算の【参照先】
\(= \left( \begin{array}{c} -(f(x_{+Δ}, y)-f(x,y))Δy\\ -(f(x, y_{+Δ})-f(x,y))Δx \\ ΔxΔy \end{array} \right) \)

上式から\(ΔxΔy\)(スカラーとして) を外に出せる。そして展開すると：
\(G=\frac{-(f(x_{+Δ}, y)-f(x,y))}{Δx}\)
\(H=\frac{-(f(x, y_{+Δ})-f(x,y))}{Δy}\)

\(= \left( \begin{array}{c} -\color{fuchsia}{ \frac{(f(x_{+Δ}, y)-f(x,y))}{Δx} }\\ -\color{fuchsia}{ \frac{(f(x, y_{+Δ})-f(x,y))}{Δy} }\\ 1 \end{array} \right) \)\(ΔxΔy\) \(= \left( \begin{array}{c} -G\\ -H\\ 1 \end{array} \right) \)\(ΔxΔy\)

上のベクトル成分からベクトルの大きさ（絶対値）が求まる：

\(ΔS\)\(=|\bv{B} \x \bv{C}|\) \(=\sqrt{G^2+H^2+1}\)\(ΔxΔy\) \(:(a)\)

\(\Delta x\) と \(\Delta y\) を 0 に近付けると：

ⓐ以下は x とy における偏微分

\(\pder{f}{x}=\displaystyle \lim_{\Delta x \to 0} \frac{(f(x_{+Δ}, y)-f(x,y))}{Δx}\)
\(\pder{f}{y}=\displaystyle \lim_{\Delta y \to 0} \frac{(f(y_{+Δ}, y)-f(x,y))}{Δy}\)

ⓑ\(ΔS\)は\(dS\) となる。
ⓐ と ⓑから式(a)の変形として：
\(dS=\sqrt{(\pder{f}{x})^2 + (\pder{f}{y})^2+1 \ }\) \(dxdy\)　

\(\b{A} \cdot \b{n}\) (①) の導出
1)ベクトル\(\b{A}\)は：

\(\b{A}(x,y,z)=(A_x,A_y,A_z)\)である。

2)単位法線ベクトル\(\b{n}\)求める。

微小面積の面要素\(dS\) を張るベクトルは次の「 B、C の偏微分」です。
(B,C の偏微分は面要素\(dS\)の接ベクトルです)

\(\pder{\b{B}}{x}\)\(=(1,0,\pder{f}{x})\) \( \ \) \(\pder{\b{C}}{y}\)\(=(0,1,\pder{f}{y})\)
\(\pder{\b{B}}{x} \x \pder{\b{C}}{x}\) \(=\left( \begin{array}{c} 1\\ 0\\ \pder{f}{x} \end{array} \right) \) \( \x \) \( \left( \begin{array}{c} 0 \\ 1 \\ \pder{f}{y} \end{array} \right) \) \(=\left( \begin{array}{c} -\pder{f}{x}\\ -\pder{f}{y} \\ 1 \end{array} \right) \) \(=(-\pder{f}{x},-\pder{f}{y},1) \)

ベクトル積の大きさ（絶対値）は（3平方定理を用いて）：

\(| \pder{\b{B}}{x} \x \pder{\b{C}}{x} |\) \(=\sqrt{ (-\pder{f}{x})^2+(\pder{f}{y})^2+1 } \)

2つのベクトル積は面要素\(dS\)の法線ベクトルです、これを自身の絶対値で割ると単位法線ベクトルになります。

\(n=\displaystyle \frac{ \pder{\b{B}}{x}　\x \pder{\b{C}}{y} }{ |\pder{\b{B}}{x}　\x \pder{\b{C}}{y}| } \) \(=\displaystyle \frac{(-\pder{f}{x},-\pder{f}{y},1)}{\sqrt{ (\pder{f}{x})^2+(\pder{f}{y})^2+1 }}\)

積分関数を先に計算すると：

\( \b{A} \cdot \b{n}\ dS\) \(=\displaystyle \b{A} \cdot \frac{(-\pder{f}{x},-\pder{f}{y},1)}{\sqrt{ (\pder{f}{x})^2+(\pder{f}{y})^2+1 }}\) \( (\sqrt{ (\pder{f}{x})^2+(\pder{f}{y})^2+1 }\ )dx\ dy\)
\(=\displaystyle \b{A} \cdot (-\pder{f}{x},-\pder{f}{y},1) dx\ dy \) \(=\displaystyle (A_x,A_y,A_z) \cdot (-\pder{f}{x},-\pder{f}{y},1) dx\ dy \)
内積演算すると
\(=\displaystyle (-A_x\pder{f}{x}-A_y\pder{f}{y}+ A_z)　dx\ dy \)

\(\therefore\underline{\dsii_S \b{A}\cdot\b{n} dS }\) \(=\underline{ \dsii_D (-A_x \pder{f}{x} -A_y \pder{f}{y} + A_z) \ dxdy }\) \(\ \scriptsize {(❶)}\)
\(\ \small {これで ❶ の証明ができました}\)

注：\(\b{n}dS\) のことを面要素ベクトルといいます。( \(\b{n}\)はベクトル、\(dS\)はスカラー)
ここでは面積要素 \(dS\) を使い説明しましたが、本によっては、またこの先に「面要素ベクトル \(\b{n}dS\)」用いて説明することがあります。

次に曲面の近似が接平面であり、細かく分割した接平面の\(ΔS\)と\(\b{A}\cdot \b{n}\)の積の、領域についての総和がベクトルの面積分の概念から面積分を求めます。
具体的に「ベクトル場の\(\b{A}\)」,「曲面の\(\bv{r}(u,v)\)」,「曲面の接平面の接線ベクトル\(\b{B},\ \b{C}\)」を用いてベクトル場の面積分を求めていきます。

曲面は\(\bv{r}(u,v)=\bv{r}(x(u,v),y(u,v),z(u,v))\)で表している。
参考:以下はベクトル積の性質です。

・ベクトル積 \(\b{B} \x \b{C}\)はΔS の法線である。
・ベクトル積の絶対値 \(|\b{B} \x \b{C}|\)はΔS の面積である。

　 fig3 接平面と\(\Delta S\)　

ベクトル場の面積分2

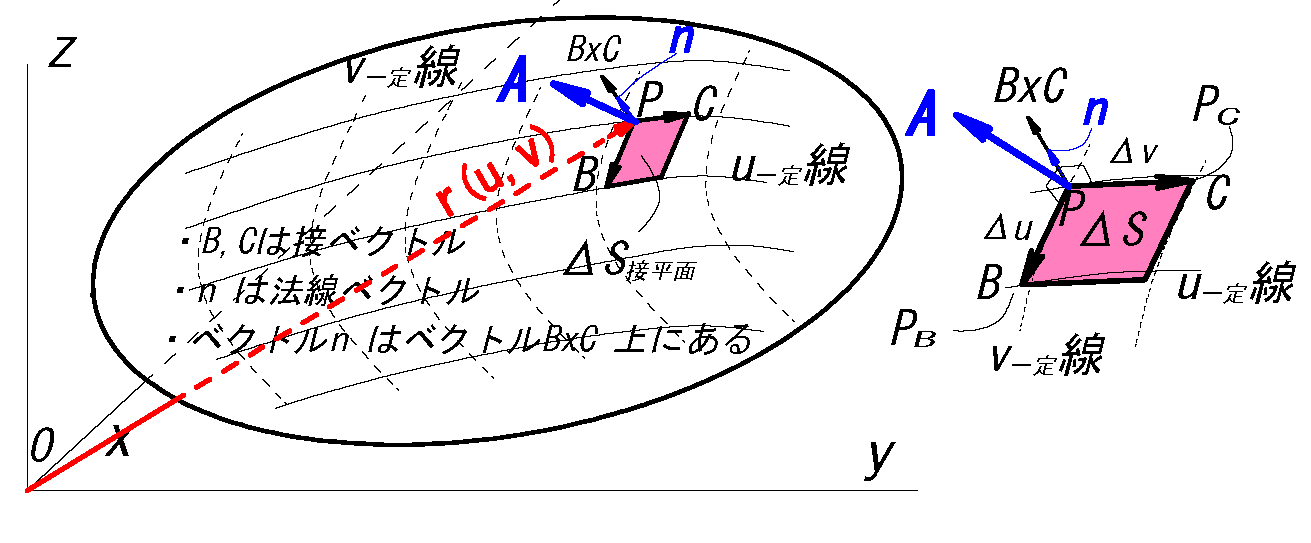
fig3 においてベクトル場\(A(x,y,z)\)と曲面\(S\) をパラメータ\(u,v\)を使い表わす。

・曲面S は\(\bv{r}(u,v)\) で表す。
・\((x,y,z)\)は\(u,v\)で決まる。

ベクトル場:
\(\b{A}(x,y,z)=\bv{A}(u,v)\)\(=\bv{A}(x(u,v),y(u,v),z(u,v))\)
曲面S:
\(\bv{r}(u,v)\)\(=\bv{r}(x(u,v),y(u,v),z(u,v))\)
このときベクトル場\(A(u,v)\) の曲面S における面積分は次式により定義される。

\(　\dsii_S \b{A} \cdot \b{n} dS\) \(=\dsii_D \b{A} \cdot (\pder{\bv{r}}{u} \x \pder{\bv{r}}{v}) \ dudv\) \(\ :❷\)

式 ❷ の導出

２つの接線ベクトルが張る平面が接平面です。　その接線ベクトルは次式で表せる。
\(\dspder{r}{u}\) \(,\quad \) \(\dspder{r}{v}\)
これは接線の傾きであり、単位接線ベクトルだから面積素\(\Delta S\)を構成する接線ベクトル \(\bv{B},\bv{C}\)と\(\Delta S\)は:

\(\bv{B}=\dspder{r}{u}\Delta u\) \(,\quad \) \(\bv{C}=\dspder{r}{v}\Delta v\)
\(\Delta S=|\bv{B} \x \bv{C}|\)\(=|\dspder{r}{u}\Delta u \x \dspder{r}{v}\Delta v|\) \(=|\dspder{r}{u} \x \dspder{r}{v}|\Delta u \Delta v\)

外積の性質から\(\Delta u\ \Delta v \) は正のスカラーだから絶対値の外に出せる。
\(\Delta u\)\(,\) \(\Delta v\) を 0 に近付けると：
\(\color{red}{ dS=|\dspder{r}{u} \x \dspder{r}{v}|du dv }\)
ここから前回の「スカラー場の面積分」と異なります。まず、単位法線ベクトルを求めます。
B C のベクトル積はΔSの法線だから、 ΔSの単位法線ベクトルは次から得られる。
（ベクトルの外積は\(dS\)の法線ベクトル、これを自身の絶対値で割ると厳密な単位法線ベクトルが得られる）
\(　\b{B}\x \b{C}\)　\(=\dspder{r}{u}\Delta u \x \dspder{r}{v}\Delta v\) \(=(\dspder{r}{u} \x \dspder{r}{v})\Delta u \Delta v\)

\( \color{blue}{ \b{n}}=　\dsfr {\b{B}\x \b{C} }{ |\b{B} \x \b{C}| } \) \(=　\dsfr {(\dspder{r}{u}\x \dspder{r}{v} ) \Delta u \Delta v}{|\dspder{r}{u}\x \dspder{r}{v}| \Delta u \Delta v } \) \(=\color{blue}{　\dsfr {(\dspder{r}{u}\x \dspder{r}{v} ) }{|\dspder{r}{u}\x \dspder{r}{v}| } }\)

\(　\dsii_S \b{A} \cdot \b{n} dS \) \(=\dsii_D \b{A} \cdot \color{blue}{\dsfr {(\dspder{r}{u}\x \dspder{r}{v} ) }{|\dspder{r}{u}\x \dspder{r}{v}|} }\) \(\color{red}{|\dspder{r}{u} \x \dspder{r}{v}|du dv }\)
\(=\dsii_D \b{A} \cdot (\pder{\bv{r}}{u} \x \pder{\bv{r}}{v}) \ dudv\) \(\ :❷\)
式❷の導出ができました。

例題1
☞重積分(累次積分)を忘れた方は：【参照先】

　 fig4 曲面全体　

　 fig5 積分領域　

ベクトル場\(\underline{ \b{A}=(x,2y,z-2) }\) の次の曲面S における面積分を求めよ。
積分すべき曲面S は次の曲面とx,y,z軸の交わりで作る曲面。
\(S:\ \underline{ z=f(x,y)=2-2x-y }\) （空間内の平面です）
　

式❶を使い解く：

\(　\dsii_S \b{A}\cdot\b{n} dS\) \(=\dsii_D (-A_x \pder{f}{x} -A_y \pder{f}{y} + A_z) \ dxdy\) \(\ :❶\)

\(A_x=x,\ A_y=2y,\ A_z=-2x-y\)
\( A_z=z-2=(2-2x-y)-2=-2x-y \)

以上より

\((A_x,\ A_y,\ A_z)=(x,\ 2y,\ -2x-y)\)
\(\pder{f}{x}=-2\) \(\ ,\ \) \(\pder{f}{y}=-1\)

従い、式❶は以下になる：

\(\dsii_S \b{A}\cdot\b{n} dS\) \(=\dsii_D \{-x(-2)-2y(-1)+(-2x-y) \} dx dy \)
\(= \dsii_D　(2x+2y-2x-y) dxdy　\) \(=\dsi_0^1 \dsi_0^{2-2x} y\ dy\ dx \)
\(=\dsi_0^1\ \left[ \dsfr{1}{2}y^2 \right]_0^{2-2x} dx\)

\( \dsfr{1}{2} \left[ y^2 \right]_0^{2-2x}\) \(=\dsfr{1}{2}(2-2x)^2\) \(=\dsfr{1}{2}(4-8x+4x^2)\) \(=(2-4x+2x^2)\)

\(=\dsi_0^1\ (2-4x+2x^2) dx\) \(=\left[2x-\dsfr{4}{2}x^2+\dsfr{2}{3}x^3 \right]_0^1\) \(=(2-\dsfr{4}{2}+\dsfr{2}{3})\) \(=\dsfr{2}{3}\)

例題2
問題は例題1と同じだが、パラメータを使う式❷により解く

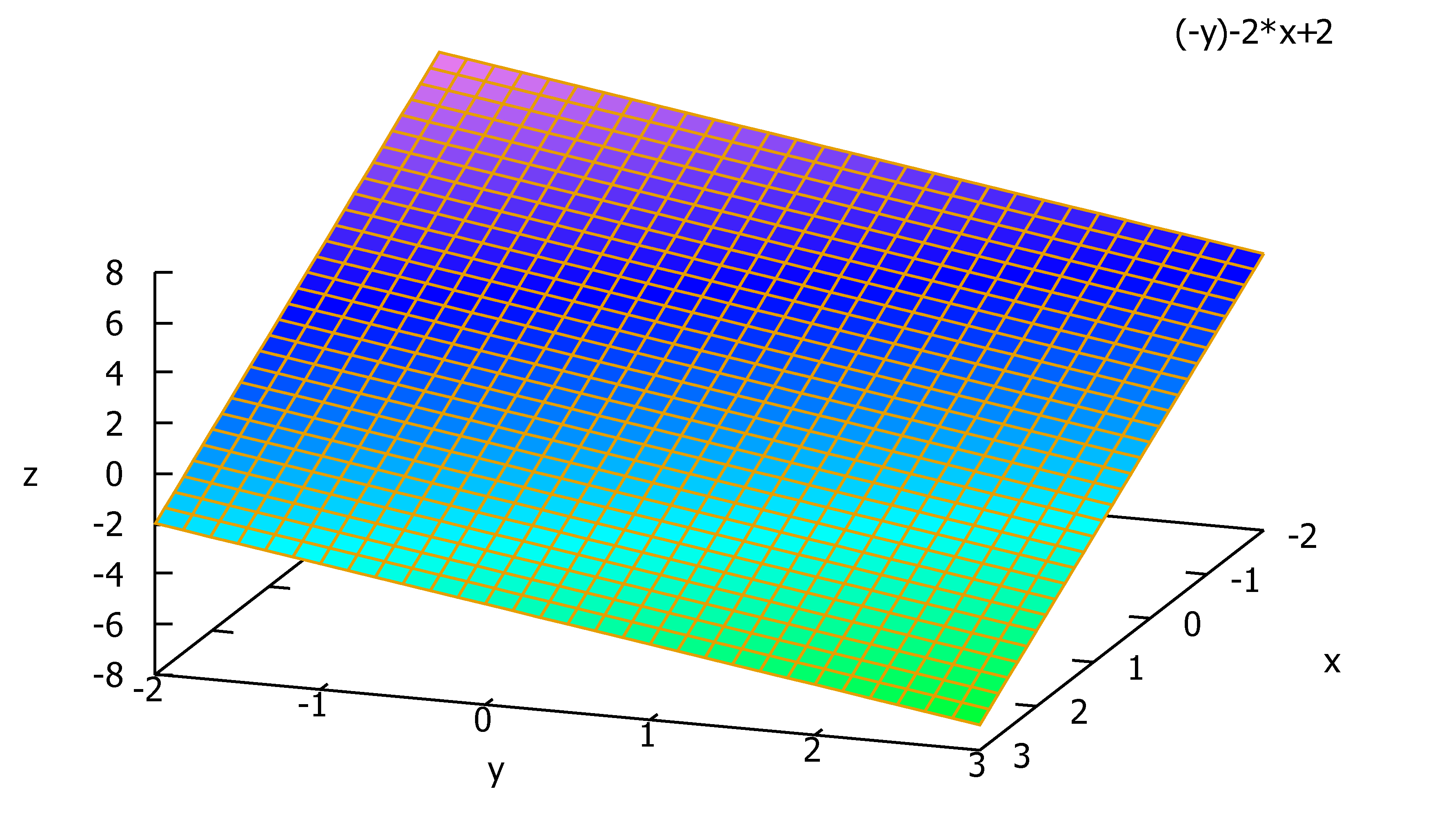
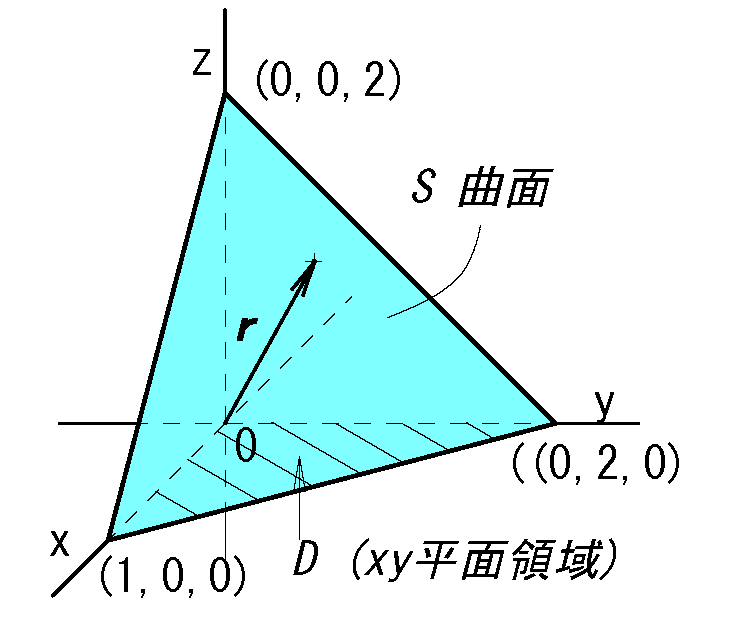
ベクトル場\(\b{A}=(x,2y,z-2)\) の次の曲面S における面積分を求めよ。
積分すべき曲面S は次の曲面とx,y,z軸の交わりで作る曲面。
\(S:z=f(x,y)=2-2x-y\)

\(x=u,\ y=v\) とすると \(z=2-2u-v\) ※a
ここでは曲面S をベクトル\(\b{r}\)で表す。（fig5)
\(\b{r}\)は原点を中心に、変数(u,v)で決まる位置ベクトルです。
\(\underline{ \b{r}=(u,v,2-2u-v)}\) \( \quad ( p(x,y,z) )\)

\(\b{A}=(x,2y,z-2)=(u,2v,(2-2u-v)-2))\)より
\(\underline{ \b{A}=(u,2v,-2u-v) }\) \(=(A_x,\ A_y,\ A_z)\)

これより以下のような式展開となる。

\(\pder{r}{u}=(1,0,-2)\) \(\ ,\ \) \(\pder{r}{v}=(0,1,-1)\)

\(ndS=\pder{r}{u} \x \pder{r}{u} dudv\)
\(=\left( \begin{array}{c} 1\\ 0\\ -2 \end{array} \right) \) \( \x \) \( \left( \begin{array}{c} 0 \\ 1 \\ -1 \end{array} \right) dudv \) \(=\left( \begin{array}{c} 2\\ 1\\ 1 \end{array} \right) dudv \)

\(A \cdot ndS=(u,\ 2v,\ 2-2u-v)\cdot (2,1,1)dudv \) \(=(2u+2v+(-2u-v))dudv\)\(=v\ dudv\)

これを式❷に代入して重積分を解く。
\(　\dsii_S \b{A} \cdot \b{n} dS\) \(=\dsii_D \b{A} \cdot (\pder{\bv{r}}{u} \x \pder{\bv{r}}{v}) \ dudv\) \(\ :❷\)

※a より
\(D:\ u=0 \to 1\) \(\quad\) \(v=0 \to 2-2u\)

\(　\dsii_S \b{A} \cdot \b{n} dS\) \(=\dsii_D　v\ dudv\) \(=\dsi_0^1 (\dsi_0^{2-2u} v　\ dv)\ du\)
\(=\dsi_0^1 \left[　\dsfr{1}{2} v^2 \right]_0^{2-2u} du\) \(=\dsi_0^1 \dsfr{1}{2} (2-2u)^2 du\) \(=2 \dsi_0^1 (u^2-2u+1) du\)
\(=2 \left[ \frac{u^3}{3}-u^2+u \right]_0^1 \) \(=2(\frac{1}{3}-1+1)\)\(=\dsfr{2}{3}\)
答えは例題1 と同じになりました。

coffe

[コーヒーブレイク/閑話］…お疲れさまでした