この数列を見ても、とても規則性は分かりませんね!
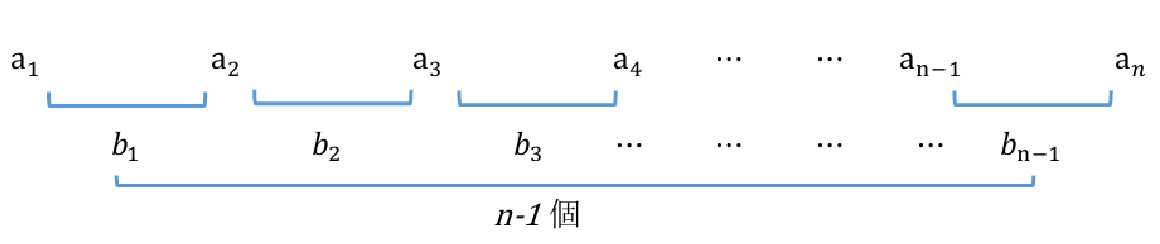
以下に、この数列の階差数列を求めていきます。
1回目の階差数列:
\(\{b_n\}=2,\ 3,\ 5,\ 8,\ 12,\ 17,\ 23,\ 30,\ \cdots\)
これでも規則性がみえません
2回目の階差数列:
\(\{c_n\}=1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7, \ \cdots\)
これで規則性がみえした。初項1、交差1 の等差数列ですね。
(等差数列の一般項の公式( (\( b_n=a_1+(n-1)d \) )
これから一般項を求めていきます。
\(\{c_n\} \)の一般項は:
\(\underline{ c_n=1+(n-1)1=n } \)
\(\{b_n\} \)の一般項は:
\( { b_n} =b_1+\displaystyle \sum_{ k = 1 }^{ n-1 } c_k =2+\displaystyle \sum_{ k = 1 }^{ n-1 }n \)
\( \underline{ =2+ \frac{1}{2}n(n-1)} \) \( \underline{ = 2+\frac{1}{2}n^2-\frac{1}{2}n }\)
\(\{a_n\} \)の一般項は:
\( { a_n} =a_1+\displaystyle \sum_{ k = 1 }^{ n-1 } b_k \)
\(=3+\displaystyle \sum_{ k = 1 }^{ n-1 }(2+\frac{1}{2}n^2-\frac{1}{2}n) \)
\(=3+\displaystyle \sum_{ k = 1 }^{ n-1 }2 + \displaystyle \sum_{ k = 1 }^{ n-1 } \frac{1}{2}n^2
-\displaystyle \sum_{ k = 1 }^{ n-1 } \frac{1}{2}n \)
\(=3+ 2\displaystyle \sum_{ k = 1 }^{ n-1 }1 + \frac{1}{2} \displaystyle \sum_{ k = 1 }^{ n-1 } n^2
-\frac{1}{2}\displaystyle \sum_{ k = 1 }^{ n-1 } n \)
\(=3+ 2(n-1)\cdot 1\) \( + \frac{1}{2}(\frac{1}{6}(n-1)n(2n-1))\) \( -\frac{1}{2} \cdot \frac{1}{2} (n-1)n \)
\(=3+(2n-2)\) \( + \frac{1}{12}n (2n^2-3n+1)\) \( -\frac{1}{4}(n^2-n) \)
\(=(1 +2n)\) \( + (\frac{1}{6}n^3 +\frac{1}{4}n^2 + \frac{1}{12}n)\) \( -(\frac{1}{4}n^2-\frac{1}{4}n) \)
\( \underline { =\frac{1}{6}n^3 - \frac{2}{4}n^2 + \frac{7}{3}n +1 }\)
【確認】
初項は3 です。
(求めた式より n = 1 のとき \(a_1=3\) )
この一般項は n=1でも成り立ち、
\(\ (n\geq1) \)
となります。