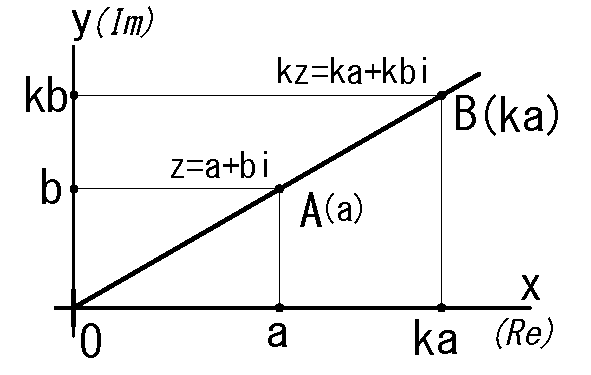はじめに
虚数は実数で表せない数を表すため導入された概念, これは 2乗して負になる数, \(x^2=-1\) の解
\(x=\sqrt{-1}\) のことです。
虚数は英語の"imaginary number" 想像上の数,大きさなどが見えない数, 現実の生活からかけ離れた抽象的な数ですが, 実は物理学から電気工学(交流理論)まで多くの分野, 身近なところではコンピューターグラフィックス, 先端技術では量子力学などに使われ, 不可欠な存在になっています。
複素数を利用すると, 単位円内での複素数の回転により三角関数の加法定理,ド・モアブルの定理が導出できます。
ある数をa を2乗して負になる数, 例えば \(x^2=-1\) の解は\(x=\sqrt{-1 }\) となり, 実数の定義域では
解無しの数です。
そこで
2乗して -1 となる数を
虚数, \(\st{i=\sqrt{-1 } }\) を
虚数単位といい, \(\st{i^2=-1}\) となる。
さらに次式で表せる数を
複素数 \(\st{z}\) といいます。
a,b は実数として
\(\ul{z=a+bi}\)…\(\s{❶}\)
・複素数の
a は実部, b は虚部 という。
・\(b= 0\) のとき \( \st{z=a}\) は
実数。
・\(b\ne 0\) のとき\(\ z=a+bi\) を
虚数(複素数でもある)という。
・\(b\ne 0,\ a=0\) のとき\(\ z=b\ i\) を
純虚数という。
複素数の極形式
次式❷は複素数の
極形式です。
極形式とは動径 r (原点O と点A までの距離)と偏角 θの成分\(A(r,θ)\) により複素数を表す式。
極座標の成分は\(A(r,θ)\)で表し、直交座標の成分は\(A(a,b)\)で表す。
極形式は複素数の回転の動きを表現するのに都合がよい。
直交座標の\(z=a+bi\) に対し
極形式は:
\(\ul{z=r(cosθ+isinθ)}\)…\(\s{❷}\)
\(r=|z|=\s{ \sqrt{a^2+b^2} }\)
\( θ=sin^{-1}(\frac{b}{r}) \)
\( a=rcosθ,\ b=rsinθ \)
θ はzの偏角という。 \( 0\le θ\lt 2\pi \)
偏角(argument)の記号は \(arg\ z\) で表す。
我々は自然数からはじめ,整数, 有理数, 無理数 に拡張し, それらを包含した実数が数直線を形成している, 虚数に数直線にあたるものは何か? それがfig1 の虚軸であり, 数直線の原点0点を中心に90°回転した線, すなわち垂線です。
横軸の実軸と縦軸の虚軸に複素数を表す平面を
複素平面(ガウス平面ともいう)といいます。
実数は1次元の世界, 複素数は実数と虚数の2次元の世界になります。
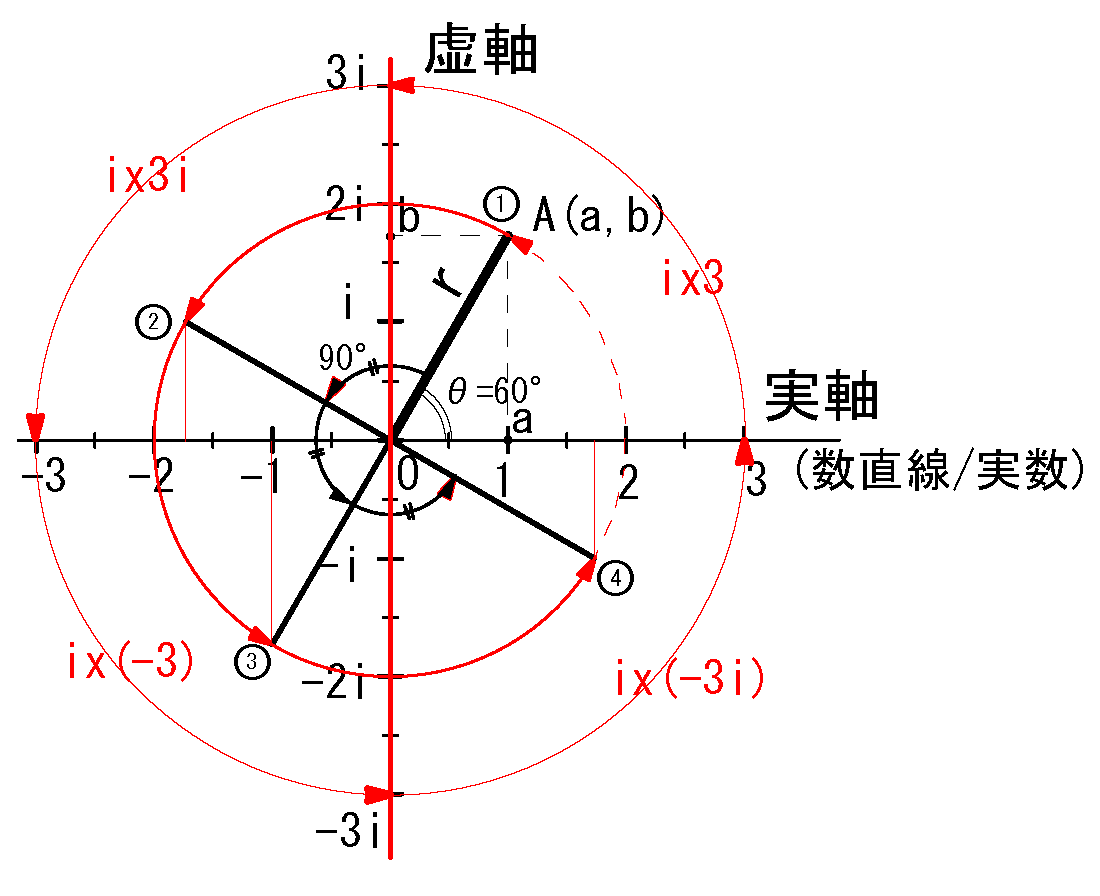
fig1 数直線と虚軸
原点O を中心に90° 回転した虚軸の点\(3\ i\) に移ることです。(fig1の赤の円)
これにより数直線(実軸)の1次元から,実数と虚数の2次元の世界に変わります。
さて,数直線上の3 をi倍、さらにi 倍していくどうなるか:
・数直線上の3 を\(i\) 倍すると\(i\x 3=3i\) に…左に90° 回転(※)した虚軸の点\(3\ i\) に移ります。
(※)反時計方向に回転を示す
・さらに\(3i\) を\(i\) 倍すると \(i\x 3i=-3i^2=-3\) に…左に90° 回転した点, 実軸の\(-3\) に移ります。
・さらに\(-3\) を\(i\) 倍すると \(i\x -3=-3i\) に…左に90° 回転した点, 虚軸の\(-3\ i\) に移ります。
・さらに\(-3i\) を\(i\) 倍すると \(i\x -3i=-3i^2=3\) に…左に90° 回転した点(スタート点), 実軸の3 に移ります。
この結果は \(i\) を4回掛けると一周(360°回転)して元の点に戻りました。
\(r=2 ,θ=\frac{ \pi}{3}\)の複素数
\(z=2(cos\frac{ \pi}{3}+i\ sin\frac{ \pi}{3})\)
①初期状態 偏角θ=\(\frac{ \pi}{3}\)
②[\(i\x ①\)]の結果:偏角 \(\to θ+\frac{\pi}{2}\)
③[\(i\x ②\)]の結果:偏角 \(\to θ+\frac{2\pi}{2}\)
④[\(i\x ③\)]の結果:偏角 \(\to θ+\frac{3\pi}{2}\)
さらにi を掛けると初期状態①に戻る。
①[\(i\x ④\)]の結果:偏角 \(\to θ+2\pi\)(※)
(※) \(\scriptsize{∵cosθ=cos(θ+2\pi),sinθ=sin(θ+2\pi)}\)
•実数または複素数に\(\st{i}\) を掛けるとは反時計方向に90°回転の操作に相当する。
•\(\st{-i}\) を掛けるとは逆の時計方向に90°回転の操作となる。
複素数の四則演算に進む前に
共役な複素数とその性質を学びます。
共役な複素数
複素数\(z=a+bi\) に対し\(\st{ \ol{ z }=a-bi }\) を
共役な複素数と言います。
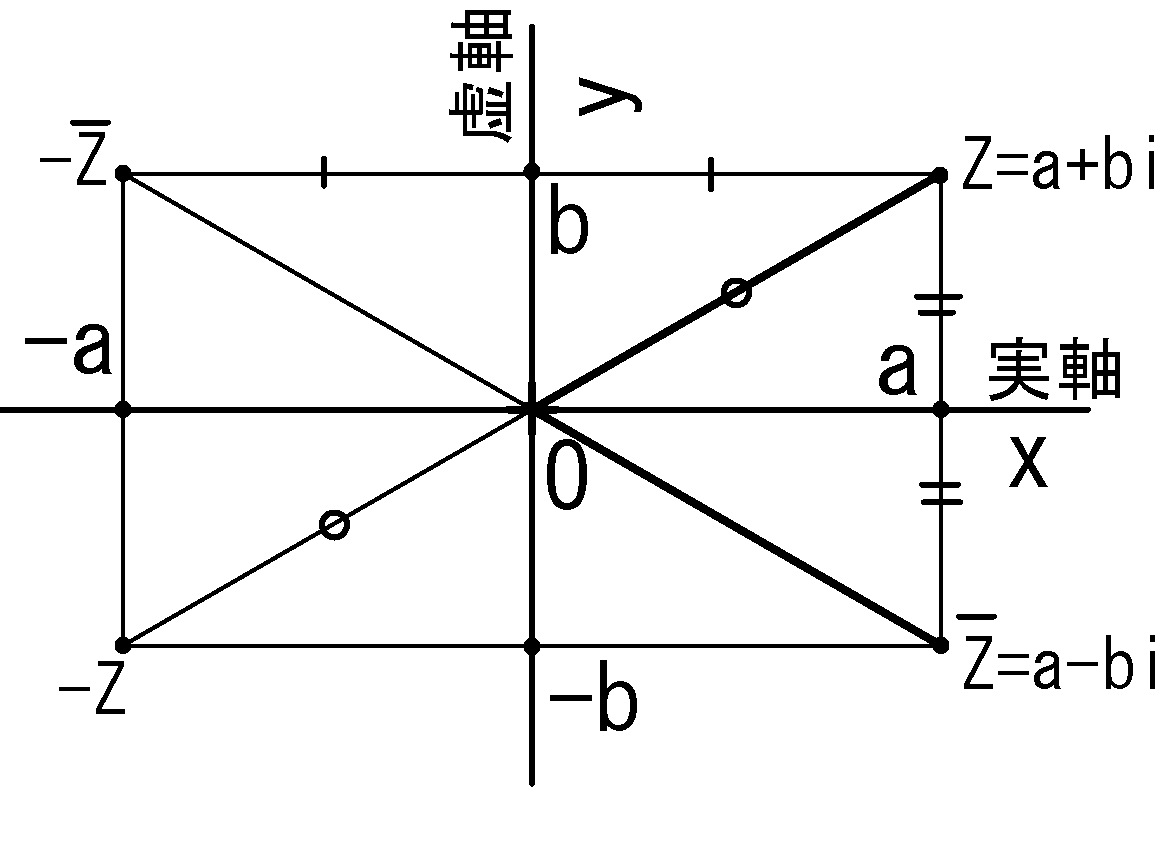
fig2 共役な複素数
fig2について:
・\(\ol{ z }\) はx軸に関して対称
・\(-z\) は\(z\) と原点\(O\) に関して対称
・\(-\ol{ z }\) は\(z\) とy軸に関して対称
共役な複素数の性質
任意の複素数\(z,w\)に関して次の性質がある。
1) \(\ol{z+w}=\ol{z}+\ol{w}\)
2) \(\ol{z-w}=\ol{z}-\ol{w}\)
3) \(\ol{zw}=\ol{z} \ \ol{w}\)
4) \(\ol{(\dsfr{z}{w})}=\dsfr{\ol{z}}{\ol{{w}}}\)
5) \( \ol{\ol{z} }=z \) :共役を2回のとき元に戻る
6) \(z+\ol{z}=\)実数 :複素数とその共役な複素数の和は実数
7) \(\ol{z^n}=(\ol{z})^n\)
8) \(z=\ol{z} \Longleftrightarrow\) \(z\) が実数
( \(z=\ul{a}+0\ i\) )
9) \(z=-\ol{z} \Longleftrightarrow\) \(z\) が純虚数
(\(z=0+\ul{b\ i}\) )
演算例
(上記 1),2) の導出例)
\(z=a+bi\)\(,\quad w=c+di\)について以下の計算をする。
\(\s{1_1}:\ \ol{z+w}= \ol{a+bi+c+di}\) \(=\ol{(a+c)+(b+d)i}\) \(=(a+c)-(b+d)i\)
\(\s{1_2}:\ \ol{z}+\ol{w}=\ol{a+bi}+\ol{c+di}\) \(=a-bi+c-di\) \(=(a+c)-(b+d)i\)
\(\s{2_1}:\ \ol{z w}= \ol{(a+bi)(c+di)}\) \(=\ol{(ac-bd)+(bc+ad)i}\)\(=(ac-bd)-(bc+ad)i\)
\(\s{2_2}:\ \ol{z}\ \ol{w}\)\(= (a-bi)(c-di)\)\(=(ac-bd)-(bc+ad)i\)
複素数\(z=a+bi\) について下式を \(z\) の絶対値 \(|z|\)といいます。
\(|z|=\sqrt{a^2+b^2}\)…\(\s{❸}\)
また, 絶対値\(|z|\) は原点O と\(z\) の点との距離でもある。
複素数の絶対値の性質
複素数の絶対値\(|z|\)に関して次の性質がある。
1) \(|z|=0 \Longleftrightarrow z=0\)
\(\ \scriptsize{(同値)}\)
2) \(|z|=|-z|=|\ol{z}|\)
3) \(z\ol{z}=|z|^2\)
4) \(|z_1z_2|=|z_1||z_2| \)
5) \(|\dsfr{z_1}{z_2}|=\dsfr{|z_1|}{|z_2|}\)
2)と3)の証明
2) \(|z|=|-z|=|\ol{z}|\)
\(|z|=\sqrt{a^2+b^2}\)
\(|-z|=|-a-bi|=\sqrt{(-a)^2+(-b)^2}\)\(=\sqrt{a^2+b^2}\)
\(|\ol{z}|=|a-bi|=\sqrt{(a)^2+(-b)^2}\)\(=\sqrt{a^2+b^2}\)
3)\(z\ol{z}=|z|^2\)
\(z\ol{z}=(a+bi)(a-bi)\)\(=a^2+b^2\)
\(|z|^2=(\sqrt{a^2+b^2})^2 \) \(=a^2+b^2\)
複素平面上の2点間の距離は次のように絶対値を使い求められる。
複素数\(z_1=a+bi\) と\(z_2=c+di\) の距離は下図より
\(\sqrt{(c-a)^2+(d-b)^2}\)
また \(z_2-z_1=(c-a)+(d-b)i\) から
上式は \(|z_2-z_1|\) であることが分かる。
一般に複素平面上の
2点間の距離は:
\(\large{ |z_2-z_1|=\sqrt{(c-a)^2+(d-b)^2} }\)…\(\s{❹}\)
である。
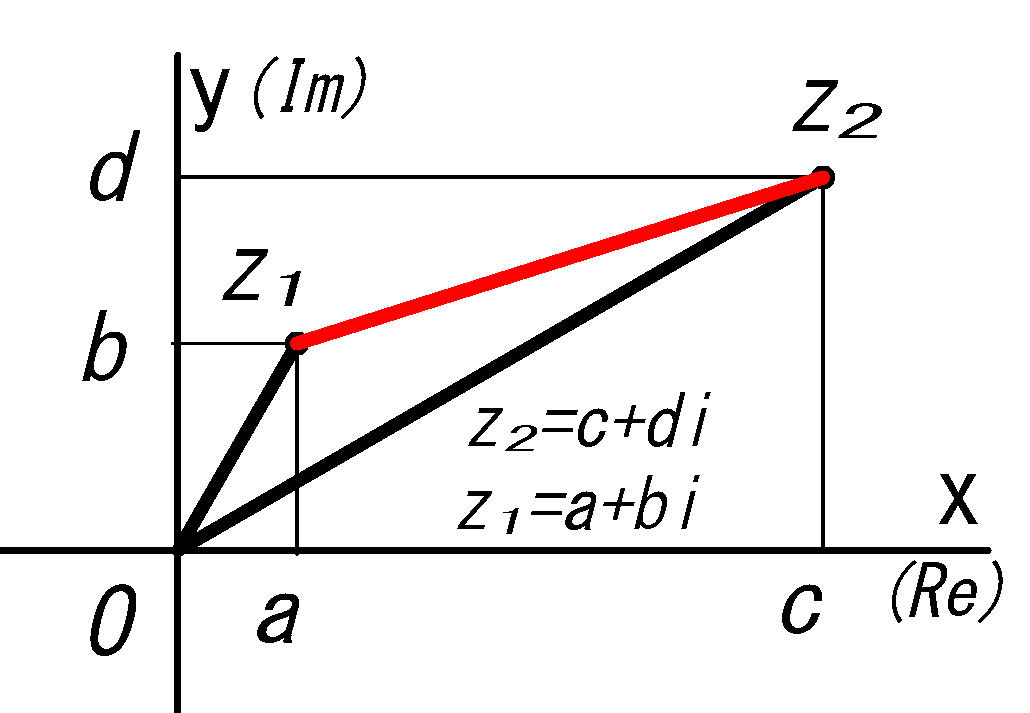
fig3 2点間の距離
複素数の実数倍
実数\(k\) と複素数\(z=a+bi\) について\(kz=ka+kbi\) が成り立つ。但し\(a\ne 0\)
図形的な意味は下図の点A と点B で実部と虚部との比がおなじなので原点O, 点A, 点Z は
同一直線上にあります。
この直線上の点は複素数zの
実数倍の複素数を表します。
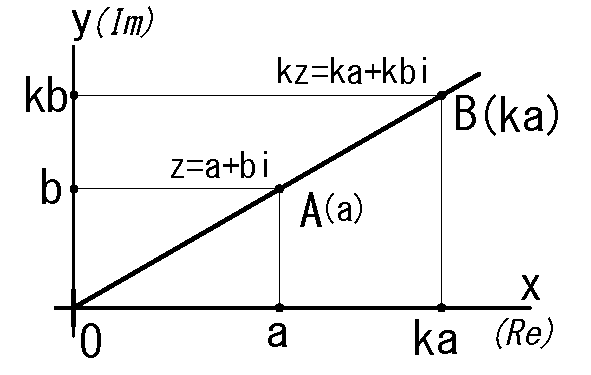
fig4 実数倍
複素数の四則演算の加減算はベクトルの演算とよく似てます、乗除算は複素数特有の演算です。
複素数の加減算
\(z_1=a+bi\)\(,\quad z_2=c+di\) として
\(z_1+z_2=a+bi+c+di\)\(=(a+c)+(b+d)i\)
\(z_1-z_2=a+bi-(c+di)\)\(=(a-c)+(b-d)i\)
図示方法は
加算:\(z_1\)を座標(c,d)=(1,2)の位置に平行移動する。
(下図 の左側\(z_3\)が加算結果)
減算:\(z_1\)を座標(-c,-d)=(-1,-2) の位置に平行移動する。
(下図 の右側\(z_3\)が減算結果)
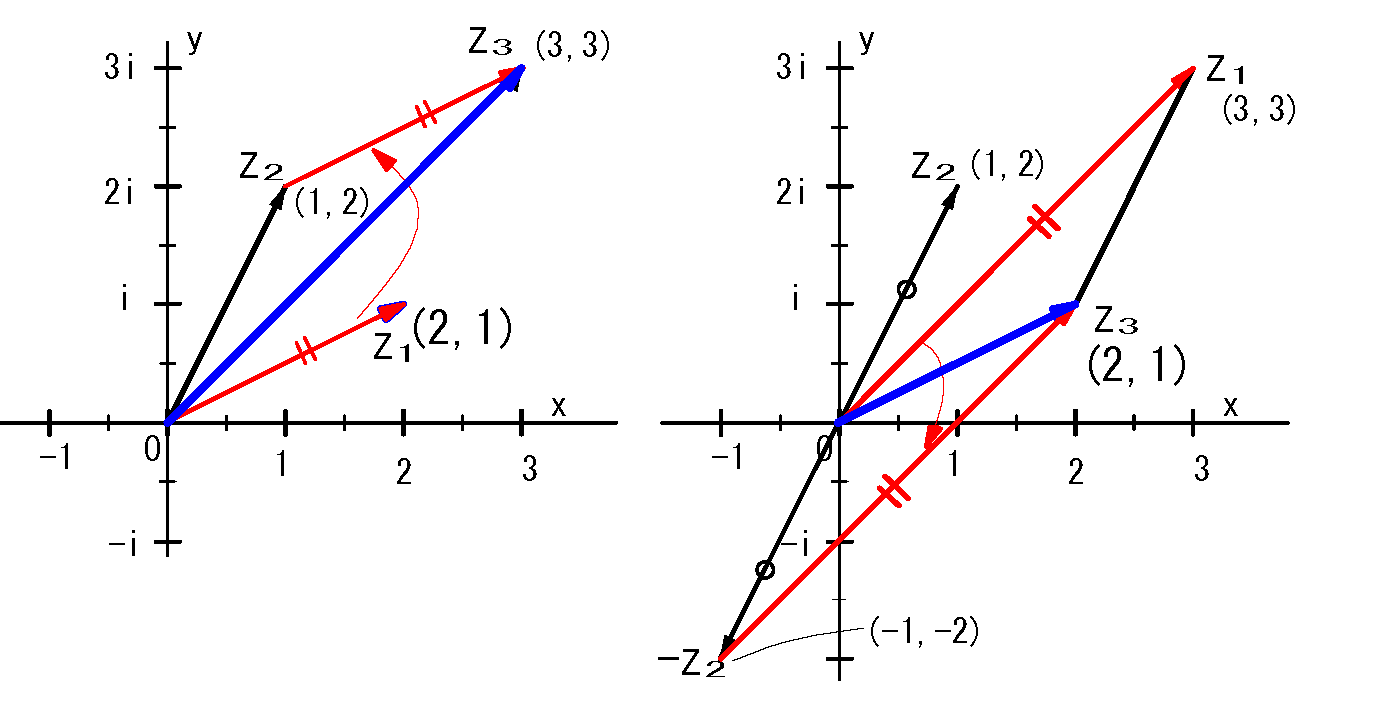
fig5 加減算
複素数の乗除算
複素数の乗除算には先に述べた極形式により演算します。
次の複素数の積を求める。
\(z_1=r_1(cosθ_1+isinθ_1)\)
\(z_2=r_2(cosθ_2+isinθ_2)\)
但し\(r_1=|z_1|,\ r_2=|z_1|\)
\(\ul{z_1 z_2}=r_1(cosθ_1+isinθ_1)\)\(\cdot r_2(cosθ_2+isinθ_2)\)
\(=r_1 r_2[(cosθ_1 cosθ_2+i^2 sinθ_1 sinθ_2)\)\(+i(cosθ_1sinθ_2+sinθ_1cosθ_2)]\)
\(=r_1 r_2[\color{red}{(cosθ_1 cosθ_2-sinθ_1 sinθ_2)}\)\(+i\ \color{blue}{(cosθ_1sinθ_2+sinθ_1cosθ_2)}]\)
赤字部,青字部は三角関数の加法定理により簡単化
☞加法定理
【参照先】
\(\therefore \ul{z_1 z_2}=r_1 r_2[\color{red}{(cos(θ_1 + θ_2)}\) \(+i\ \color{blue}{ (sin(θ_1+θ_2))} ]\)
乗算\(z_1z_2\) の結果 は複素数の点\(C\), この位置が図形的な意味を与える。
(下図 左側参照)
・絶対値: \(|z_1z_2|=r_1 r_2\)
・偏角: \(arg(z_1z_2)=θ_1+θ_2\)
・\(z_1\)に対して絶対値は\(r_2\)倍, 偏角は\(θ_2\)増えた。
・動径の回転位置が\(θ_2\) 進み,大きさが拡大/縮小したイメージ。
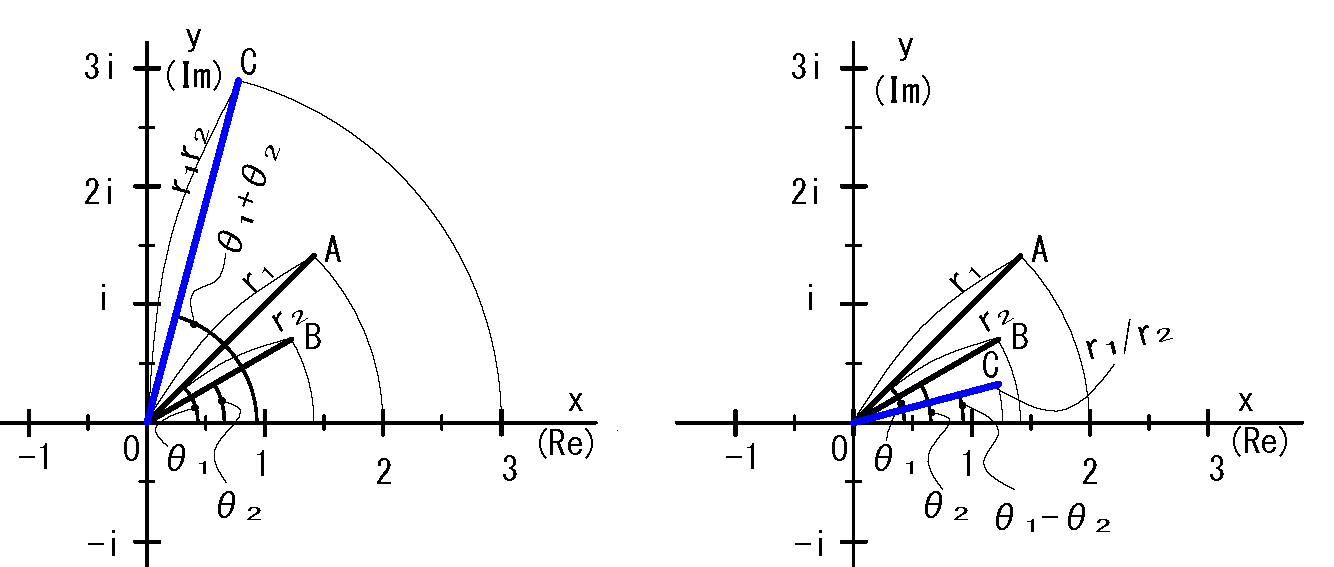
fig6 乗除算
次に複素数の商を求める。
分母にi があるときは無理数の有理化のように分母の実数化を行う。
\(\dsfr{z_1}{z_2}\)\(=\dsfr{z_1}{z_2}\ \ul{ \dsfr{(cosθ_1+isinθ_1)}{(cosθ_2+isinθ_2)} }\)
以下は下線部の展開
分母の共役複素数を掛け分母の実数化をする
\(\dsfr{(cosθ_1+isinθ_1)}{(cosθ_2+isinθ_2)}\)
\(=\dsfr{(cosθ_1+isinθ_1)(\color{red}{cosθ_2-isinθ_2})}{(cosθ_2+isinθ_2)(\color{red}{cosθ_2-isinθ_2})}\)
分母\(=(cos^2θ_2+sin^2θ_2)=1\)
\(=(\color{red}{(cosθ_1 cosθ_2+sinθ_1 sinθ_2)}\)
\(+i(\color{blue}{(sinθ_1 cosθ_2- cosθ_1 sinθ_2)}\)
分子は加法定理により簡単化
\(=(\color{red}{cos(θ_1-θ_2)})+i(\color{blue}{sin(θ_1-θ_2)})\)
\(\therefore \dsfr{z_1}{z_2}\)\(=\dsfr{r_1}{r_2}[cos(θ_1-θ_2)+i\ sin(θ_1-θ_2)]\)
除算\(\frac{z_1}{z_2}\) の結果 は複素数の点\(C\),この位置が図形的な意味を与える。
(上図 右側参照)
・絶対値: \(|\frac{z_1}{z_2}|=\frac{|r_1|}{|r_2|}\)
・偏角: \(arg(\frac{z_1}{z_2})=θ_1-θ_2\)
・\(z_1\)に対して絶対値は\(\frac{1}{r_2}\)倍, 偏角は\(-θ_2\)分減る。
・動径が\(θ_2\)分 逆転し(位相遅れ) ,大きさが拡大/縮小したイメージ。
例題3 次の複素数を極形式で表せ
1)\(z=1+\sqrt{3}\ i\) (参照 fig1 点A)
次の如く, 絶対値\(|z|\) と偏角\( arg\ θ \) を求める。
解:\(r=|z|=\s{ \sqrt{1^2+\sqrt{3}^2} }=2\)
\(arg\ θ=sin^{-1} (\frac{\sqrt{3}}{2})=\frac{\pi}{3}\)(=60°)
\(\therefore z=2(cos\dsfr{\pi}{3}+isin \dsfr{\pi}{3})\)
☞三角比
【参照先】
2)\(z=1-\sqrt{3}\ i\)
注:虚数部が負に注意
解:\(r=|z|=\s{ \sqrt{1^2+\sqrt{3}^2} }=2\)
\(arg\ θ=sin^{-1} (\frac{-\sqrt{3}}{2})=-\frac{\pi}{3}\)(=-60°)
\(\therefore z=2(cos(-\dsfr{\pi}{3})-isin(-\dsfr{\pi}{3}))\)
第4象限にあり,上記の1)とx軸に関し対称な複素数である
次の距離をもとめよ。
次の複素数\(z_1,\ z_2\)が示す2点間の距離
\(z_1=2+i,\ z_1=-2-i\)
\(z_1-z_2=2+i-(-2-i)=4+2i\)
\(|z_1-z_2|=\sqrt{4^2+2^2}=2\sqrt{5}\)
例題5 次の複素数を乗除算せよ
\(z_1=2(cos\dsfr{\pi}{4}+i\ sin\dsfr{\pi}{4})\)
\(z_2=\sqrt{2}(cos\dsfr{\pi}{6}+i\ sin\dsfr{\pi}{6})\)
解:乗算(参照 fig6 左図)
\(z_1 z_2=2\sqrt{2}\ [cos(\frac{\pi}{4}+\frac{\pi}{6})+i\ sin(\frac{\pi}{4}+\frac{\pi}{6})]\)
\(=2\sqrt{2}\ [cos\frac{5\pi}{12}+i\ sin\frac{5\pi}{12} ] \)
\( \therefore z_1 z_2=2\sqrt{2}\ (cos\dsfr{5\pi}{12}+i\ sin\dsfr{5\pi}{12})\)
解:除算(参照 fig6 右図)
\(\frac{z_1}{z_2} = \frac{2}{\sqrt{2}}\ [cos(\frac{\pi}{4}-\frac{\pi}{6})+i\ sin(\frac{\pi}{4}-\frac{\pi}{6})]\)
\(=\frac{2}{\sqrt{2}} \frac{\sqrt{2}}{\sqrt{2}}\ ( cos\frac{\pi}{12}+i\ sin\frac{\pi}{12} ) \)
\(\therefore \dsfr{z_1}{z_2}=\sqrt{2}\ ( cos\dsfr{\pi}{12}+i\ sin\dsfr{\pi}{12} ) \)
…以上