ファラデーの考えた電気力線 電気力管・ファラデー管
導体の表面張力
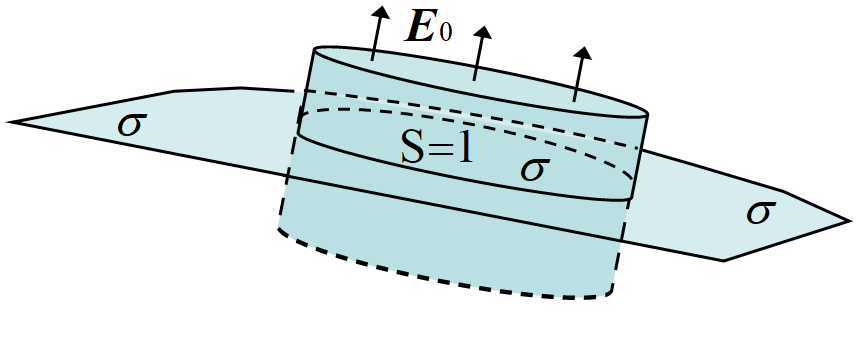
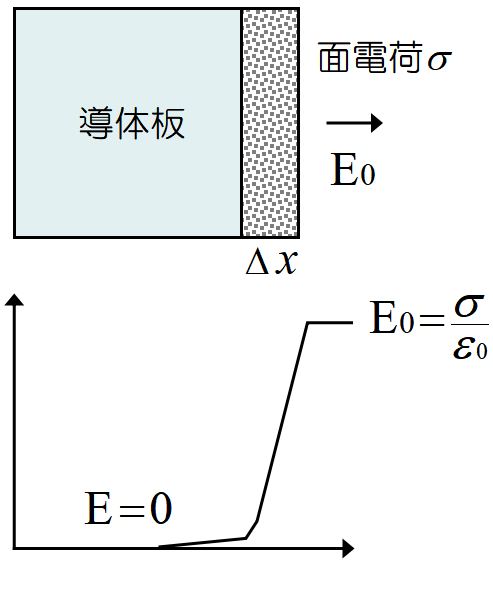
導体が面密度\(~\sigma~\)の電荷を持つとき, 電荷は表面に分布し, 内部の電場は 0 である。表面の電場は面に垂直で,
\[E_0=\frac{\sigma}{\varepsilon_0}\]
である。
この時, 導体表面に存在する電荷には, 導体の単位面積当たり
\[F=\sigma\frac{1}{2}E_0=\frac{1}{2}\varepsilon_0E^2_0\;[N/m^2]\tag{1}\]
の力が働く。\(F=\sigma E_0~\)ではなく, \(1/2~\)が付く理由は次による。(ファインマン物理III p97)
極板面上の電荷が薄い層を成しているとすると, 場は層の内側の境界での値\(~0~\)まで変化している。面電荷に働く平均の場は\(~E_0/2~\)である。これが \(1/2~\)が付く理由である。
電荷の薄い層内の体積電荷密度を\(~\rho~\)としたとき, \(~\sigma=\rho\triangle x~\)が表面電荷密度である。
マックスウェル応力 張力と圧力
ファラデーは多くの力線の様子を観察し, 力線は線の方向に縮み, 直角方向には膨らむ性質を持つと考えるに至った。
空間には一種の弾性的性質があって, 電場は電気的なひずみを受けた弾性体のようにふるまい, 電気的な力はその中を応力として伝わる。この応力の完全な形は, 後年にマックスウェルによって与えられた。
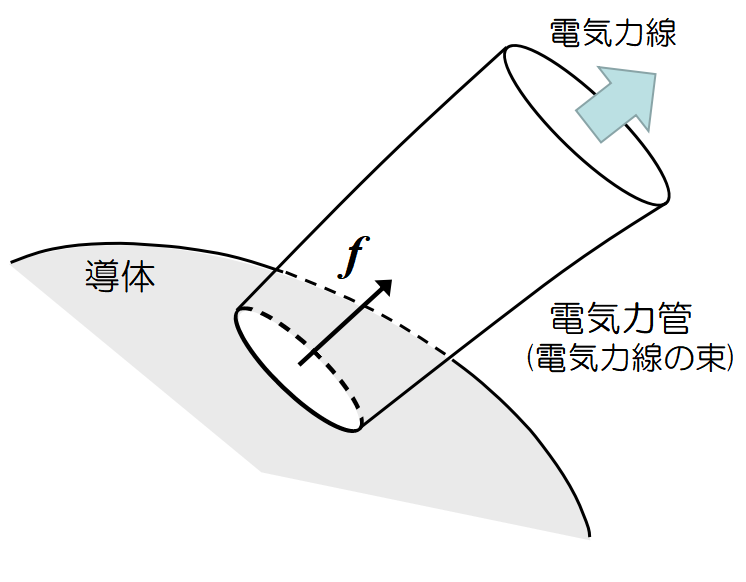
ファラデーはこの様子を, 図の様な帯電した導体表面から出る細い電気力管がゴムの様に伸縮すると考えた。
この電気力管を通して, 導体表面の電荷は電場から静電張力(1)を受ける。作用・反作用から電場は電荷から同じ力を受けることになる。しかし電場, すなわち空間には反作用を受け止める存在は無く, 反作用は空間を次々と伝わり, 電場を作っている他の電荷にまで達して,そこで反作用が受け止められる。
\(\qquad\)電気力管に沿った方向に\(\qquad\displaystyle f=\frac{1}{2}\varepsilon_0E^2_0~\)の張力
\(\qquad\)電気力管に垂直な方向に\(\qquad\displaystyle f=\frac{1}{2}\varepsilon_0E^2_0~\)の圧力
がはたらく。この張力と圧力を総称してマックスウェル応力と呼ぶ。
電荷間の力が遠隔作用的に働くのでなく, 電荷がその周りの電場を変化させ, その変化した電場を通して働くというこの近接作用的な考え方は, 多くの研究者に受け入れられ, その後の電磁気学の発展に, 豊かな実りをもたらした。
張力と圧力が等しいということ
張力と圧力が等しい, ということに疑問を持つ読者がいると思う。証明はいくつかの方法があるが, いずれも微小体積を考えて力の釣り合いを解いて得られる。ここでは(FNの高校物理マックスウェル応力→電場内の応力)から引用させて頂いた。
証明では立体角を用いる。立体角になじみのない読者に簡単に説明しておく。
\(\qquad\)平面角 \(\displaystyle \theta(rad)=\frac{L}{r}\left(=\frac{L_1}{r_1}=\frac{L_2}{r_2}=\cdots \right)\)
円周上の弧\(~L~\)と半径\(~r~\)の比。
\(\qquad\)立体角 \(\displaystyle \Omega(sr)\,\,=\frac{S}{r^2}\left(=\frac{S_1}{r^2_1}=\frac{S_2}{r^2_2}=\cdots \right)\)
球面上の面積\(~S~\)と半径\(~r^2~\)の比。
平面角\(~\theta~\)はお馴染みの角度で単位はラジアン。円弧の長さの最大は\(~2\pi r~\)なので\(~0\leqq\theta\leqq 2\pi\)。
立体角\(~\Omega~\)の単位はステラジアン。球面の面積(切取る面積の最大値)は\(~4\pi r^2~\)なので\(~0\leqq\Omega\leqq 4\pi\)。
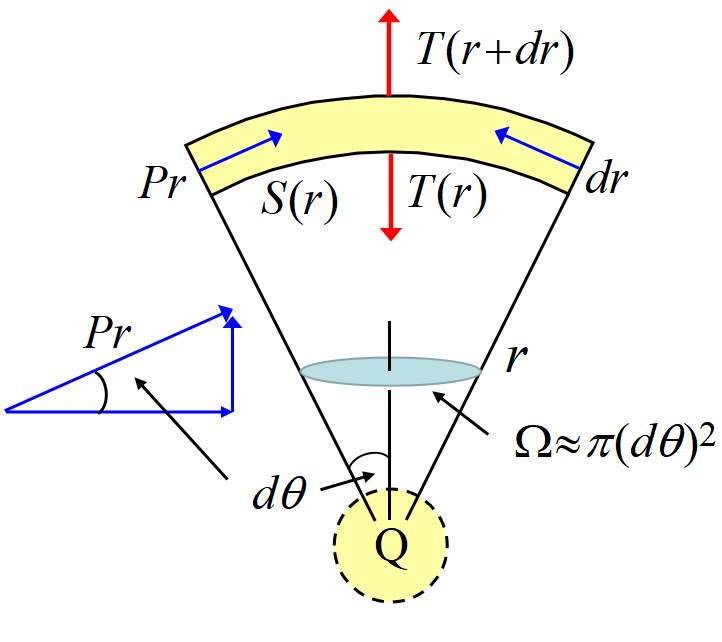
内部に電荷\(~Q~\)を含む半径\(~r~\)の導体の, 球殻の微小体積部分の力の釣合いを考える。
半径\(~r~\), 立体角\(~\Omega~\)の面\(~S(r)~\)に働く静電力は, 表面の電場を\(~E_r~\)とすると, (1)より
\[T=\frac{\varepsilon_0}{2}E_r^2 S(r)\]
である。\(S(r)=r^2\Omega\), \(\displaystyle E_r=\frac{Q}{4\pi\varepsilon_0 r^2}\)を用いて整理すると,
\[T=\frac{\varepsilon_0}{2}\left(\frac{Q}{4\pi\varepsilon_0}\right)^2\x \frac{\Omega}{r^2}\]
\(r\to r+dr~\)のとき, 静電張力\(~T~\)の変化は
\[\begin{align}
dT&=\frac{\varepsilon_0}{2}\left(\frac{Q}{4\pi\varepsilon_0}\right)^2
\left(-2\frac{1}{r^3}dr\right)\Omega \\
&=\frac{\varepsilon_0}{2}\left(\frac{Q}{4\pi\varepsilon_0 r^2}\right)^2
(-2rdr)\Omega \\
&=-\frac{\varepsilon_0}{2}E_r^2(2rdr)\Omega \tag{2}
\end{align}\]
変化はー(マイナス)だから, \(T~\)は球の中心を向き, 電気力管に沿って働く張力である。
一方単位面積当たりの圧力を\(~P_r\)とすると, 球殻の微小体積部分の側面に働く圧力の動径方向成分は
\[\begin{align}
P&=P_r\,sind\theta\x 2\pi r d\theta dr \\
&=P_r\,d\theta\,2\pi r\,d\theta\,dr \\
&=P_r\,2rdr\,\Omega \quad(\gets\Omega=\pi(d\theta)^2) \tag{3}
\end{align}\]
\(2\pi r d\theta dr\)は切り取り部分の側壁の面積である。体積要素に対する応力の釣合い, (2)=(3)から
\[P_r=\frac{\varepsilon_0}{2}E_r^2 \tag{4}\]
となり, 電気力管の張力と圧力は等しい。
電気力線の実在性
電気力線が実在するかどうか?哲学的に考えて結論の出る問題ではないが, 多くの例を通して考えるのが良いと思う。
筆者も多くの例を通じて, 電気力線, 場というものが単なる想像だけではないと考える様になった。
以下は「鏡像法」として良く知られており, 詳細な計算を知りたい読者はそちらを参照されたい。
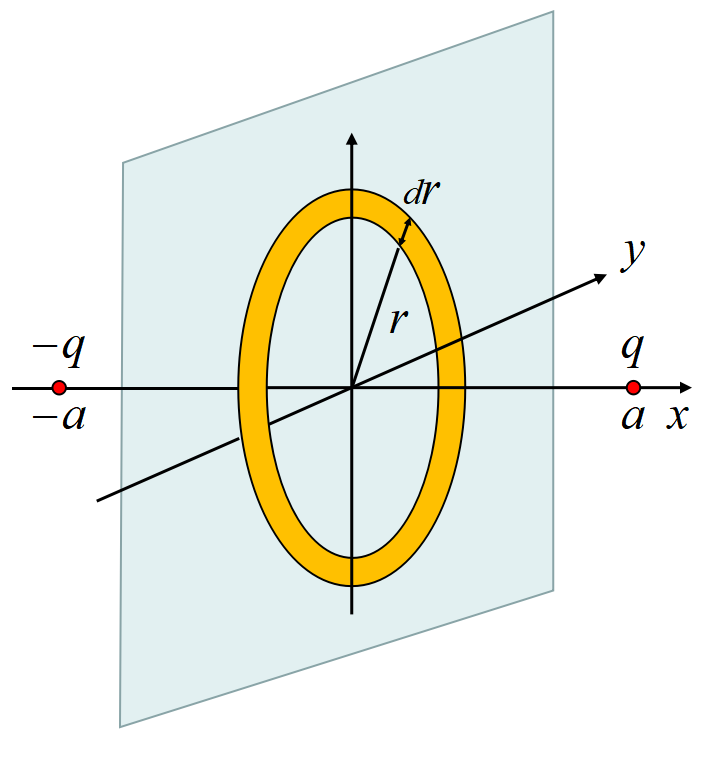
導体表面から距離\(~a,\,-a~\)に点電荷\(~q,\,-q~\)を置いたとき, この2つの電荷の引き合う力を, 電気力管の張力から求めてみよう。
位置\(~x~\)におけるポテンシャルは, 点電荷\(~q,\,-q~\)の作るポテンシャルの和だから
\[\phi=\phi_q+\phi_{-q}=\frac{q}{4\pi\varepsilon_0} \left(\frac{1}{\sqrt{(x-a)^2+r^2}} -\frac{1}{\sqrt{(x+a)^2+r^2}}\right) \]
\(x~\)方向の電場成分は\(~x~\)で偏微分して,
\[E_x=-\dd{\phi}{x}=\frac{q}{4\pi\varepsilon_0}\left(\frac{x-a}{\{(x-
a)^2+r^2\}^{\frac{3}{2}}}-\frac{x+a}{\{(x+a)^2+r^2\}^{\frac{3}{2}} }\right)\]
導体表面では\(~x=0~\)とおいて
\[\Vec E=\frac{q}{4\pi\varepsilon_0}\frac{-2a}{(a^2+r^2)^{\frac{3}{2}}}\bm{n}\]
ここで, \(\bm{n}~\)は導体表面の外向きの単位法線ベクトルである。また, 点電荷から導体表面におろした垂線の足を\(~O~\)とし, 導体表面上\(~O~\)からの距離を\(~r~\)とした。
要するに, 点電荷\(~q~\)から電気力管が伸びてきて, 張力\(~\frac{1}{2}\varepsilon_0 E^2~\)の働く領域を導板上に作る訳である。
中心からの距離が\(~r~\)の点における張力は(4)を(1)に代入して
\[\sigma=\frac{-a^2q^2}{8\pi^2\varepsilon_0}\frac{1}{(a^2+r^2)^3}\]
\(~r\sim r+dr~\)の面積が\(~2\pi r dr~\)だから, 導体面全体では
\[F=\int_{0}^{\infty}\sigma\,2\pi r dr
=\frac{q^2}{4\pi\varepsilon_0}\frac{1}{(2a)^2}\]
で, 電荷\(~q\)から伸びてきた電気力管が導体表面に及ぼす張力の合計が, 距離\(~2a~\)隔てて置かれた2つの電荷\(~q~\)と\(~-q~\)の間に働くクーロン力の大きさに等しい。
電磁場の運動量 質量を持たない「場」の運動量とは?
ファインマンのパラドックス 運動量保存則は破れたか?
電荷を持った2つの粒子の運動を考える。それぞれの電荷を\(~q_1,\,q_2~\), 質量を\(~m_1,\,m_2~\), 位置座標を\(\bm{x}_1,\,\bm{x}_2~\)とする。2つは互いに垂直にそれぞれ速度\(~\bm{\upsilon}_1,\,\bm{\upsilon}_2~\)で等速直線運動をしている。
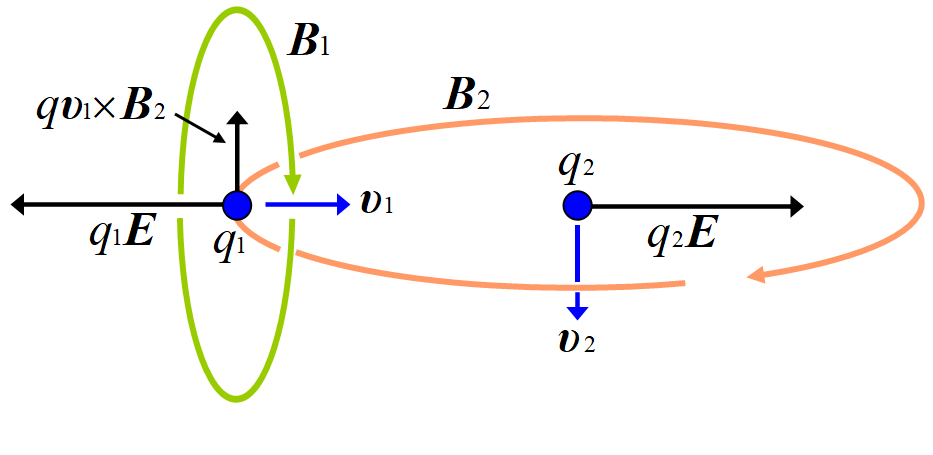
電荷\(~q_2~\)は電荷\(~q_1~\)(以下\(~q_2,\,q_1~\))の前方で\(~q_1~\)が通
る直線軌道を横切った。粒子2が丁度, 粒子1の運動直線上通過する瞬間において粒子2によって粒子1に働く力およびその逆を考える。各電荷に働く力は電場および磁場によるローレンツ力である。\(~q_1~\)はその運動直線にそう磁場を作らないから, \(~q_2~\)に働くのは\(~q_1~\)による電場だけである。一方\(~q_1~\)には\(~q_2~\)による電場だけではなく, \(~q_2~\)の作る磁場\(~\Vec B~\)の中で運動しているから, その磁場による力も受ける。力は図のようになる。\(~q_1~\)と\(~q_2~\)とに働く電場の力は, 大きさが等しく向きは反対である。しかし\(~q_1~\)には磁場\(~\Vec B_2~\)による上向きの磁場の力があり, \(~q_2~\)には横向きの力がない。作用・反作用が成り立っていない様に見える。つまり運動量保存則は成り立たないのだろうか?
運動方程式を立てて検討してみよう。粒子1の運動方程式は
\[m_1\frac{d^2\bm{x}_1}{dt^2}=q_1\Vec E_2(\bm{x}_1)+q_1\bm{\upsilon}_1\x \Vec B_2(\bm{x}_1)\tag{5}\]
である。ここに\(~\Vec E_2(\bm{x}_1)~\)および\(~\Vec B_2(\bm{x}_1)~\)は, 粒子2が粒子1の位置に作る, 電場および磁場である。それぞれ
\[\begin{align}
\Vec E_2(\bm{x})&=\frac{q_2}{4\pi\varepsilon_0}\frac{\bm{x}-\bm{x}_2}{|\bm{x}-\bm{x}_2|^3} \\
\Vec B_2(\bm{x})&=\frac{q_2\mu_0}{4\pi}\frac{d\bm{x}_2}{dt}\x
\frac{\bm{x}-\bm{x}_2}{|\bm{x}-\bm{x}_2|^3}
\end{align}\]
これを(5)式に代入して
\[m_1\frac{d^2\bm{x}_1}{dt^2}
=\frac{q_1q_2}{4\pi\varepsilon_0}\frac{\bm{x}_1-\bm{x}_2}{|\bm{x}_1
-\bm{x}_2|^3}
+\frac{q_1q_2\mu_0}{4\pi}\bm{\upsilon}_1\x \left(\bm{\upsilon}_2\x
\frac{\bm{x}_1-\bm{x}_2}{|\bm{x}_1-\bm{x}_2|^3}\right) \tag{6}\]
粒子2は(6)式の 1 と 2 を入れ替えて
\[m_2\frac{d^2\bm{x}_1}{dt^2}
=\frac{q_1q_2}{4\pi\varepsilon_0}\frac{\bm{x}_2-\bm{x}_1}{|\bm{x}_2
-\bm{x}_1|^3}
+\frac{q_1q_2\mu_0}{4\pi}\bm{\upsilon}_2\x \left(\bm{\upsilon}_1\x
\frac{\bm{x}_2-\bm{x}_1}{|\bm{x}_2-\bm{x}_1|^3}\right) \]
これらの式の両辺の和を取ると, 電場の項がキャンセル(作用・反作用)され
\[\begin{align}
m_1\frac{d^2\bm{x}_1}{dt^2}+m_2\frac{d^2\bm{x}_1}{dt^2}
&=\frac{q_1q_2\mu_0}{4\pi}
\left[ \bm{\upsilon}_1\x \left(\bm{\upsilon}_2\x \frac{\bm{x}_1-\bm{x}_2}{|\bm{x}_1-\bm{x}_2|^3}\right)
+\bm{\upsilon}_2\x \left(\bm{\upsilon}_1\x \frac{\bm{x}_2-\bm{x}_1}{|\bm{x}_2-\bm{x}_1|^3}\right) \right] \\
&=\frac{q_1q_2\mu_0}{4\pi|r_{12}|^3}
[\bm{\upsilon}_1\x \{\bm{\upsilon}_2\x (\bm{x}_1-\bm{x}_2)\}
+\bm{\upsilon}_2\x \{\bm{\upsilon}_1\x (\bm{x}_2-\bm{x}_1)\}]
\end{align}\]
右辺[ ]内第2項で \(~\bm{x}_2-\bm{x}_1~\)は粒子\(~q_1~\)から\(~q_2~\)へ向かうベクトルで, 速度ベクトル\(~\bm{\upsilon}_1~\)と同じ向きだから, \(\bm{\upsilon}_1\x (\bm{x}_2-\bm{x}_1)~\)はゼロ。\(\bm{\upsilon}_1\x \{\bm{\upsilon}_2\x (\bm{x}_1-\bm{x}_2)\}\)は明らかにゼロではないから, 右辺全体はゼロではない。すなわち,
\[m_1\frac{d^2\bm{x}_1}{dt^2}+m_2\frac{d^2\bm{x}_2}{dt^2}\neq0 \]
が得られる。この左辺を粒子1および2の運動量\(~\bm{p}_1~\)および\(~\bm{p}_2~\)を用いて書くと,
\[\frac{d(\bm{p}_1+\bm{p}_2)}{dt}\neq 0 \]
となり, \(\bm{p}_1+\bm{p}_2~\)は保存しないことが確認できる。
厳密にいえば, 運動量が保存されないのではなく, 「粒子の運動量は保存されない」である。
では, 保存される運動量とは一体何なのであろうか?
自己場 自分自身が周囲に作りだす電場への影響
唐突であるが, 自己場に触れておかなければならない。電荷が周りの電荷から受ける力→応力テンソル→電磁波の運動量と話が進む。そのためには自己場の考察が必要である、
電荷が周りの電荷から力を受ける場合, その電荷自身が周囲に作る電場の影響はどう取り込めばよいのであろうか?
結論から言えば, 何も考えなくて良い。点電荷で普通に\(~E=q/r^2~\)とすると, \(r=0~\)の点で電場が無限大の特異点になってしまう。
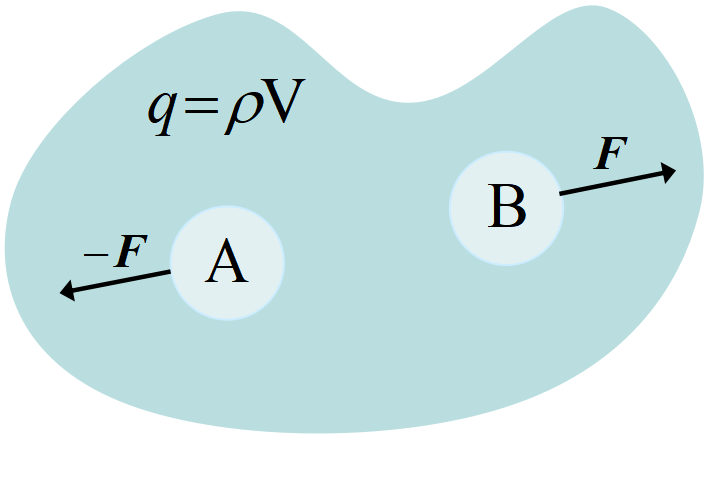
そこで電荷が小領域に雲のように密度\(~\rho~\)で分布して, 全体で電荷\(~q~\)になっていると考える。
小さな領域の中のさらに微小な領域\(~A~\)内の電荷が, 別の微小領域\(~B~\)内の電荷に力\(~F~\)を及ぼす時, 逆に\(~B~\)内の微小電荷は\(~A~\)内の電荷に\(-F~\)の力を及ぼすので, 領域全体としては力が釣り合っている。
電磁波の運動量 質量を持たない電磁波に運動量は存在するのか?
高校物理での運動量は\(~\bm{p}=m\bm{\upsilon}~\)であった。電磁場は質量を持たないので, 今までの「質量×速度」で運動量を論ずることはできない。
質量が無くとも運動量は存在すると言われても, そう簡単には納得できない。
元々ニュートンの運動方程式は運動量の時間変化が力であった。この運動方程式およびケプラーの第3法則から, 質量という物理量は, お互いに引き合う万有引力を生み出す, という発見がニュートン力学の集大成であった。
ここでは視点を変え, 運動量の時間微分が力, すなわち\(~\Vec F=d\bm{p}/dt~\)から運動量を定義しよう。
電荷\(~q~\)の粒子が電磁場から受ける力は
\[\Vec F=q(\Vec E+\bm{\upsilon}\x \Vec B)\]
である。粒子が複数存在する場合, 力はその和\(~\Vec F=\sum_{i}q_i(\Vec E+\bm{\upsilon}_i\x \Vec B)~\)となる。
粒子の分布が連続的と見なす事が出来る場合, 電荷密度\(~\rho~\), 電流密度\(~\bm{j}~\)を用いて, 次のように書ける。
\[\Vec F=\int_V(\rho\Vec E+\bm{j}\x \Vec B)\,dV \]
領域\(~V~\)内の全粒子の運動量の総和を\(~\Vec P_{粒子}~\)とすると, ニュートンの運動方程式より
\[\frac{d\Vec P_{粒子}}{dt}=\int_V(\rho\Vec E+\bm{j}\x \Vec B)\,dV \tag{7}\]
と書ける。\(\rho~\)および\(~\bm{j}\)を
\[\rho=\varepsilon_0 div\Vec E,\qquad \bm{j}=\frac{1}{\mu_0}rot\Vec B-\varepsilon_0\dd{\Vec E}{t} \]
を用いて, 「場」を表す\(~\Vec E~\)と\(~\Vec B~\)で書き換えると, 単位体積当たりの力は
\[\begin{align}
\rho\Vec E+\bm{j}\x \Vec B
&=(\varepsilon_0 div\Vec E)\Vec E
+\left(\frac{1}{\mu_0}rot\Vec B-\varepsilon_0\dd{\Vec E}{t}\right)\x \Vec B\\
&=\varepsilon_0\left(\Vec E div\Vec E-\dd{\Vec E}{t}\x \Vec B\right)-\frac{1}
{\mu_0}\Vec B\x rot\Vec B \tag{8}
\end{align}\]
となる。後々都合の良くなるよう, 外積の順序を入替え, 符号を変えた。
領域内の荷電粒子に作用する力の総和は, 領域内の電荷および電流間の相互作用と, 領域外の電荷および電流間による電磁場との相互作用の和である。領域内の電荷および電流の間に作用する力は作用反作用の法則により相殺するため, 力の総和には寄与しない。したがって領域内の電荷に作用する力の総和は, 領域外の電磁場だけによるものだけを考えれば良い。
ここで注意すべきは, (8)式の\(~\Vec E~\)および\(~\Vec B~\)は領域内の電荷密度\(~\rho~\)および電流密度\(~\bm{j}~\)から与えられるものであり, したがって領域内の物理量だけで力の総和が与えられることを示している。
ある領域\(~V~\)内の電荷\(~\rho(\bm{x})~\)が周囲から受ける力を計算する時, 自己場は無視して, 領域\(~V~\)外の電荷だけに着目すれば良かった。新しい結論は, その領域\(~V~\)外の電荷も無視して, 領域\(~V~\)内の電場\(~\Vec E~\)を使えば良いというのである。一体何を使えば良いのか混乱する。落ち着いて考えよう。
計算すべき領域\(~V~\)外の電荷は, 領域\(~V~\)内の電荷に影響を与え,
その影響は, 領域\(~V~\)内の電場に現れている。だから領域\(~V~\)内の電場を使って計算すれば良い。ということである。
ここで, ポインティング・ベクトルを導入するために, (8)式右辺の2番目の項を書き直す。先ず
\[\dd{}{t}(\Vec E\x \Vec B)=\Vec E\x \dd{\Vec B}{t}+\dd{\Vec E}{t}\x \Vec B \]
より,
\[-\dd{\Vec E}{t}\x \Vec B=-\dd{}{t}(\Vec E\x \Vec B)+\Vec E\x \dd{\Vec B}{t}=-\dd{}{t}(\Vec E\x \Vec B)-\Vec E\x rot\Vec E \]
と書き直す。式変形の最後はファラデーの法則\(~rot\Vec E=-\partial \Vec B/\partial t~\)である。(7), (8)式に代入して
\[\begin{align}
\frac{d\Vec P_{粒子}}{dt}
&=\int_V(\rho\Vec E+\bm{j}\x \Vec B)\,dV \\
&=\int_V \left[\varepsilon_0\{\Vec E div\Vec E -\dd{}{t}(\Vec E\x \Vec B)
-\Vec E\x rot\Vec E\}-\frac{1}{\mu_0}\Vec B\x rot\Vec B\right]\,dV \\
&=\int_V \left[\varepsilon_0(\Vec E div\Vec E-\Vec E\x rot\Vec E) -\frac{1}
{\mu_0}\Vec B\x rot\Vec B -\varepsilon_0\dd{}{t}(\Vec E\x \Vec B)\right]\,dV\tag{9}
\end{align}\]
時間微分の項を左辺に集めて
\[
\frac{d}{dt}\left(\Vec P_{粒子}+\int_V \varepsilon_0(\Vec E\x \Vec B)dV \right)
=\int_V \left[\varepsilon_0(\Vec E div\Vec E-\Vec E\x rot\Vec E) -\frac{1}
{\mu_0}\Vec B\x rot\Vec B\right]\,dV
\]
を得る。技巧的なところが多いが, 先人も苦労したのだろう。技巧ついでに, 右辺, 積分の被積分項に
\(\displaystyle~\frac{1}{\mu_0}\Vec B div\Vec B=0~\)を加えて
\[
\frac{d}{dt}\left(\Vec P_{粒子}+\int_V \varepsilon_0(\Vec E\x \Vec B)dV \right)
=\int_V \left[\varepsilon_0(\Vec E div\Vec E-\Vec E\x rot\Vec E)+\frac{1}
{\mu_0}(\Vec B div\Vec B-\Vec B\x rot\Vec B)\right]\,dV \tag{10}
\]
としておこう。(9)式の右辺は元々「力」であったから,
\[\frac{d}{dt}\left(\Vec P_{粒子}+\int_V \varepsilon_0(\Vec E\x \Vec B)dV \right)=\Vec F\]
これはニュートンの運動方程式であり, 粒子系の(力学的)運動量\(~\Vec P_{粒子}~\)のほかに
\[\Vec P_{field}=\int_V \varepsilon_0(\Vec E\x \Vec B)\,dV \tag{11} \]
で定義される新しい運動量が, 粒子以外の「なにものか」によって運ばれていることになる。
あとは(9)式右辺, 積分 [ ] の被積分項, 単位体積に働く, 電磁場の力の正体を突き止めるだけである!
マックスウェルの応力テンソル 電気力管の張力・圧力
静電応力テンソル (1) エレガントな解法の前に具体的イメージを掴もう!
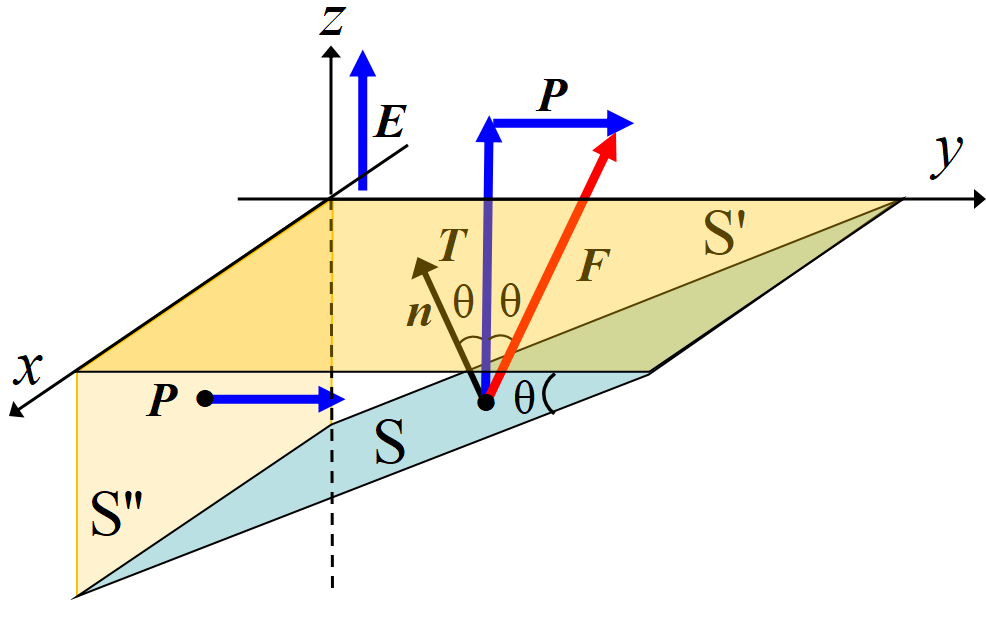
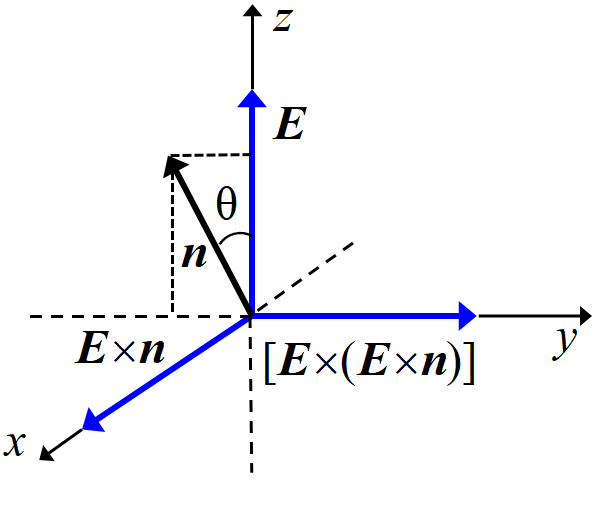
\(z~\)軸方向に向いた電場\(~\Vec E~\)の中の微小体積に働く応力を考えよう。
FN高校物理→マックスウェル応力を筆者が理解できるように改編した。
この微小体積の面積要素\(~S~\)に働く力を考える。\(~S~\)の単位法線\(~\bm{n}~\)と電場\(~\Vec E~\)のなす角を\(~\theta~\)とする。
まず電場\(~\Vec E~\)による張力であるが, (1)より, \(\displaystyle \frac{1}{2}\varepsilon_0 E^2~\)に面積要素\(~S~\)の\(~xy~\)平面への正射影\(~S'~\)を乗じたものに等しい。すなわち張力\(~T~\)は
\[T=\frac{1}{2}\varepsilon_0 E^2 S cos\theta \tag{12}\]
圧力は(張力と同じ), \(\displaystyle \frac{1}{2}\varepsilon_0 E^2~\)に面積要素\(~S~\)の\(~xz~\)平面への正射影\(~S''~\)を乗じたものに等しい。すなわち圧力\(~P~\)は
\[P=\frac{1}{2}\varepsilon_0 E^2 S sin\theta \tag{13} \]
面積要素\(~S~\)に働く応力\(~\Vec F~\)はこれら力をベクトル的に足し合わせたものである。
さて張力方向, 圧力方向のベクトルはどう表現したらよいだろうか?
(12)式の\(~E^2cos\theta~\)は\(~E^2~\)の単位法線ベクトル\(~\bm{n}~\)への正射影であるから, \((\Vec E\cdot\bm{n})\Vec E~\)が丁度, 大きさが\(~E^2 cos\theta~\)で方向が\(~\Vec E~\)のベクトルである。
\(~\varepsilon_0/2~\)をかければ, 張力ベクトル\(~\Vec T~\)となる。
もう一つの圧力方向のベクトルは工夫が必要である。\(\Vec E\x(\Vec E\x \bm{n})~\)が丁度この目的に合うベクトルである事が分かる。
\(\Vec E\x \bm{n}~\)は外積で, 大きさが\(~Esin\theta~\)である。すると\(\Vec E\x(\Vec E\x \bm{n})~\)は大きさが\(~E^2 sin\theta~\)で向きが\(~\Vec E~\)と\(~\Vec E\x \bm{n}~\)に垂直, すなわち圧力\(~\Vec P~\)と同じ向きのベクトルである。
つまり(12)式と(13)式をベクトル的に加え合わせるには,
\[\Vec F=\frac{\varepsilon_0}{2}(\Vec E\cdot\bm{n})\Vec E
+\frac{\varepsilon_0}{2}[\Vec E\x (\Vec E\x \bm{n})] \tag{14}\]
とすれば良い。これで応力\(~\Vec F~\)の電場\(~\Vec E~\)による表現が得られた。
ここでベクトル公式\(~[\Vec A\x (\Vec B\x \Vec C)]=(\Vec A\cdot\Vec C)\Vec B-(\Vec A\cdot\Vec B)\Vec C~\)を使うと, (14)式は以下のように変形できる。
\[\begin{align}
\Vec F&=\frac{\varepsilon_0}{2}(\Vec E\cdot\bm{n})\Vec E
+ \frac{\varepsilon_0}{2}[\Vec E\x (\Vec E\x \bm{n})] \\
&=\frac{\varepsilon_0}{2}(\Vec E\cdot\bm{n})\Vec E
+ \frac{\varepsilon_0}{2}[(\Vec E\cdot\bm{n})\Vec E-(\Vec E\cdot \Vec E)\bm{n}]\\
&=\varepsilon_0(\Vec E\cdot\bm{n})\Vec E
- \frac{\varepsilon_0}{2}(\Vec E\cdot \Vec E)\bm{n}
\end{align}\]
このベクトル\(~\Vec F~\)の成分は, 単位法線ベクトルを\(~\bm{n}=(n_x.n_y,n_z)~\)とすると
\[F_x=\varepsilon_0(E_xn_x+E_yn_y+E_zn_z)E_x-\frac{\varepsilon_0}{2}(E_x^2+E_y^2+E_z^2)n_x\]
\[F_x=\varepsilon_0(E_xn_x+E_yn_y+E_zn_z)E_y-\frac{\varepsilon_0}{2}(E_x^2+E_y^2+E_z^2)n_y\]
\[F_x=\varepsilon_0(E_xn_x+E_yn_y+E_zn_z)E_y-\frac{\varepsilon_0}{2}(E_x^2+E_y^2+E_z^2)n_y\]
となる。面積要素\(~S~\)の法線ベクトル\(~\bm{n}~\)が\(~(1,0,0)~\)の時, すなわち\(~x~\)軸に垂直な単位面積に働く応力の成分は,
\[\begin{align}
T_{xx}&=\varepsilon_0 E_x^2-\frac{\varepsilon_0}{2}(E_x^2+E_y^2+E_z^2)
=\varepsilon_0 E_x^2-\frac{\varepsilon_0}{2}\Vec E^2\\
T_{xy}&=\varepsilon_0 E_xE_y \\
T_{xz}&=\varepsilon_0 E_xE_z
\end{align}\]
ベクトル\(~\bm{n}~\)が\(~(1,0,0)\)だから, 上記の応力は\(~x~\)軸の正側より負側の体積要素に対して働いている力を意味する。また, \(~x~\)成分は面に垂直に働く張力であり, \(~y,\,z~\)成分は面に沿って働く剪断力である。
\(T_{xx}~\)は\(~x~\)軸に垂直な面で\(~x~\)軸方向の張力を, \(T_{xy}~\)は\(~x~\)軸に垂直な面で\(~y~\)軸方向の張力を, \(T_{xz}~\)は\(~x~\)軸に垂直な面で\(~z~\)軸方向の張力を表す。
同様にして法線ベクトル\(~\bm{n}~\)が\(~(0,1,0)\)および\(~(0,0,1)\)のとき,
\[\begin{align}
T_{yx}&=\varepsilon_0 E_yE_x \\
T_{yy}&=\varepsilon_0 E_y^2-\frac{\varepsilon_0}{2}(E_x^2+E_y^2+E_z^2)
=\varepsilon_0 E_y^2-\frac{\varepsilon_0}{2}\Vec E^2\\
T_{yz}&=\varepsilon_0 E_yE_z
\end{align}\]
および
\[\begin{align}
T_{zx}&=\varepsilon_0 E_zE_x \\
T_{zy}&=\varepsilon_0 E_zE_y \\
T_{zz}&=\varepsilon_0 E_z^2-\frac{\varepsilon_0}{2}(E_x^2+E_y^2+E_z^2)
=\varepsilon_0 E_z^2-\frac{\varepsilon_0}{2}\Vec E^2
\end{align}\]
となり, これらを行列表示した
\[
T=\varepsilon_0
\begin{pmatrix}
E_x^2-\frac{1}{2}\Vec E^2 & E_xE_y & E_xE_y \\
E_yE_x & E_y^2-\frac{1}{2}\Vec E^2 & E_yE_z \\
E_zE_x & E_zE_y & E_z^2-\frac{1}{2}\Vec E^2 \tag{15}
\end{pmatrix}\]
を
電場に対するマックスウェルの応力テンソルと呼ぶ。
この行列は自身の転置行列と一致する正方行列で対称行列と呼ぶ。対角成分を挟んで, 右上と左下が対称になっており, 応力テンソルでは必ず対称行列となる。
静電応力テンソル (2) 一般の教科書の導き方。こちらも必要。
以下の解法はエレガント過ぎるような気もするが, 静磁場のエネルギーの時もそうであったように, 磁場が関係すると, 数学的手法に頼らざるを得ない。磁荷\(~m~\)が存在しないことが, その理由と思われるが, 我々が実体験できる環境から離れるほど, このような傾向があるようだ。
電荷および電場のみが静的に存在し, 電流および磁場が存在しない場合, 領域\(~V~\)内の電荷が受ける力の総和は(7)式右辺積分の第1項だけとなる。
\[\Vec F=\int_V \rho(x)\Vec E(x)\,dV \tag{16} \]
ガウスの法則\(~div\Vec E=\rho/\varepsilon_0~\)を用いると
\[\Vec F=\varepsilon_0\int_V \Vec E div\Vec E\,dV \tag{17} \]
となる。(17)式の積分の被積分項を成分で書くと
\[\begin{align}
(\Vec E div\Vec E)_x&=\dd{}{x}\left(E^2_x-\frac{1}{2}\Vec E^2\right)
+\dd{E_x E_y}{y}+\dd{E_x E_z}{z} \tag{18} \\
(\Vec E div\Vec E)_y&=\dd{E_x E_y}{x}+\dd{}{x}\left(E^2_y
-\frac{1}{2}\Vec E^2\right)+\dd{E_y E_z}{z} \\
(\Vec E div\Vec E)_z&=\dd{E_x E_z}{x}+\dd{E_y E_z}{y}+\dd{}{z}\left(E^2_z
-\frac{1}{2}\Vec E^2\right) \\
\end{align}\]
突然(18)式が出てきてしまった。大変技巧的であるが次の式変形による。
\[\begin{align}
(\Vec E div\Vec E)_x&=E_x\left(\dd{E_x}{x}+\dd{E_y}{y}+\dd{E_z}{z}\right)\\
&=E_x\dd{E_x}{x}+E_x\dd{E_y}{y}+E_x\dd{E_z}{z}\\
&=\frac{1}{2}\left(\dd{E_x^2}{x}\right)+\dd{E_xE_y}{y}-E_y\dd{E_x}{y}
+\dd{E_xE_z}{z}-E_z\dd{E_x}{z} \\
&=\frac{1}{2}\left(\dd{E_x^2}{x}\right)+\dd{E_xE_y}{y}-E_y\dd{E_y}{x}
+\dd{E_xE_z}{z}-E_x\dd{E_x}{x} \\
&=\frac{1}{2}\left(\dd{E_x^2}{x}\right)+\dd{E_xE_y}{y}+\dd{E_xE_z}{z}
-\frac{1}{2}\dd{}{x}(E_y^2+E_z^2) \\
&=\dd{}{x}(E_x^2)+\dd{E_xE_y}{y}+\dd{E_xE_z}{z}
-\frac{1}{2}\dd{}{x}(E_x^2+E_y^2+E_z^2) \\
&=\dd{}{x}\left(E_x^2-\frac{1}{2}\Vec E^2\right)+\dd{E_xE_y}{y}+\dd{E_xE_z}
{z}\tag{19}
\end{align}\]
ふ~。3行目から4行目で, 右辺第3項目および第5項目は, \(~rot\Vec E=0~\)の成分,
\[\dd{E_x}{y}=\dd{E_y}{x},\quad \dd{E_x}{z}=\dd{E_z}{x}\]
の関係を用いた。
\[\Vec T_x=\varepsilon_0\left(E^2_x-\frac{1}{2}\Vec E^2,\; E_x E_y,\; E_x E_z\right) \tag{20} \]
で定義されるベクトル\(~\Vec T_x~\)を導入すると, (17)式は
\[F_x=\int div\Vec T_x\,dV \tag{21} \]
と表される。ガウスの発散定理を使って面積分にすると,
\[F_x=\int_{\sum}\Vec T_x\cdot\bm{n}dS=\int_{\sum}\Vec T_x\cdot d\Vec S \tag{22}\]
と書ける。ここで\(~\bm{n}~\)は\(~V~\)を取り囲む閉曲面\(~\sum~\)に垂直な単位法線ベクトルである。この式は\(~\Vec T_x\cdot\bm{n}~\)が単位面積当たりの力, すなわち圧力の\(~x~\)成分であることを示している。同様に\(~y~\)成分, \(z~\)成分は
\[\Vec T_y=\varepsilon_0\left(E_x E_y,\; E^2_y-\frac{1}{2}\Vec E^2,\;E_y E_z\right) \tag{23} \]
\[\Vec T_z=\varepsilon_0\left(E_x E_z,\; E_y E_z,\; E^2_z-\frac{1}{2}\Vec E^2\right) \tag{24} \]
で定義されるベクトル\(~\Vec T_y,\,\Vec T_z~\)を導入して,
\[F_y=\int_{\sum}\Vec T_y\cdot\bm{n}dS,\quad F_z=\int_{\sum}\Vec T_z\cdot\bm{n}dS \tag{25}\]
と書くことが出来る。(22)式および(25)式は,
\[
T=\varepsilon_0
\begin{pmatrix}
E^2_x-\frac{1}{2}\Vec E^2 & E_xE_y & E_xE_z \\
E_yE_x & E^2_y-\frac{1}{2}\Vec E^2 & E_yE_z \\
E_zE_x & E_zE_y & E^2_z-\frac{1}{2}\Vec E^2
\end{pmatrix}
\]
で定義されるテンソルを用いることにより, 次のように\(~x,y.z~\)成分をまとめて表すことが出来る。
\[\Vec F=\int_\sum \Vec T\cdot\bm{n}dS \tag{26} \]
(14)式と同じこのテンソル\(\Vec T~\)は, 静電応力テンソルと呼ばれる。
電荷に働く力を, ある領域の表面に働く応力の合計として表すことが出来ることが分かった。
電気力線には, ゴムひものように「短くなろうとする性質」すなわち張力と, 「互いに離れようとする性質」すなわち斥力がある。応力テンソルはその張力と斥力を表すものである。
静電応力テンソルは実対称行列であることに注意されたい。実対称行列はかならず直交行列により対角化され, その固有値はかならず実数となる。また異なる固有値に属する固有ベクトルは直交する。実対称行列が現れる物理現象として
慣性モーメントテンソルがある。
\(Maxwell~\)の応力テンソル 一般的な, 磁場を含む応力テンソル。
上述の例は, 体積\(~V~\)内の電荷に働く力が\(~\Vec F=q\Vec E~\)の場合, すなわち電流およびその結果である磁場の働きがない場合であった。\(~\Vec F=q(\Vec E+\bm{\upsilon}\x \Vec B)~\)の場合はどのようになるのであろうか?(9)式の被積分の項を再掲すると, 単位体積について
\[\begin{align}
\rho\Vec E+\bm{j}\x \Vec B
&=(\varepsilon_0 div\Vec E)\Vec E
+\left(\frac{1}{\mu_0}rot\Vec B-\varepsilon_0\dd{\Vec E}{t}\right)\x \Vec B\\
&=\varepsilon_0\left(\Vec E div\Vec E- \dd{\Vec E}{t}\x \Vec B\right)-\frac{1}
{\mu_0}\Vec B\x rot\Vec B \\
&=\varepsilon_0(\Vec E div\Vec E-\Vec E\x rot\Vec E) -\frac{1}{\mu_0}\Vec B\x
rot\Vec B -\varepsilon_0\dd{}{t}(\Vec E\x \Vec B)\tag{9'}
\end{align}\]
であった。先ずは電場のみに関係する力として\(~\varepsilon_0(\Vec E div\Vec E-\Vec E\x rot\Vec E)~\)の成分を計算して見よう。
\[\begin{align}
(\Vec E div\Vec E-\Vec E\x rot\Vec E)_x
&=E_x\left(\dd{E_x}{x}+\dd{E_y}{y}+\dd{E_z}{z}\right)-E_y(rot\Vec E)_z+E_z(rot\Vec E)_y\\
&=E_x\dd{E_x}{x}+E_x\dd{E_y}{y}+E_x\dd{E_z}{z}-E_y\left(\dd{E_y}{x}-\dd{E_x}{y} \right)+E_z\left(\dd{E_x}{z}-\dd{E_x}{z}s\right)\\
&=E_x\dd{E_x}{x}+E_x\dd{E_y}{y}+E_x\dd{E_z}{z}-E_y\dd{E_y}{x}+E_y\dd{E_x}{y} +E_z\dd{E_x}{z}-E_z\dd{E_z}{x} \\
&=E_x\dd{E_x}{x}-E_y\dd{E_y}{x}-E_z\dd{E_z}{x} +E_x\dd{E_y}{y}+E_y\dd{E_x}{y}
+E_x\dd{E_z}{z}+E_z\dd{E_x}{z} \\
&=\frac{1}{2}\left(\dd{E_x^2}{x}\right)-\frac{1}{2}\left(\dd{E_y^2}{x}\right)-
\frac{1}{2}\left(\dd{E_z^2}{x}\right)+\dd{E_xE_y}{y}+\dd{E_xE_z}{z} \\
&=\frac{1}{2}\left(\dd{E_x^2}{x}\right)+\dd{E_xE_y}{y}+\dd{E_xE_z}{z}
-\frac{1}{2}\dd{}{x}(E_y^2+E_z^2) \\
&=\dd{}{x}(E_x^2)+\dd{E_xE_y}{y}+\dd{E_xE_z}{z}
-\frac{1}{2}\dd{}{x}(E_x^2+E_y^2+E_z^2) \\
&=\dd{}{x}\left(E_x^2-\frac{1}{2}\Vec E^2\right)+\dd{E_xE_y}{y}+\dd{E_xE_z}{z}
\end{align}\]
と(19)式と同じ結果が得られた。
(19)式の時は, \(~rot\Vec E=0~\)を使って, 無理やり形を整えたが, 電流, 磁場があっても\(~\Vec E\x rot\Vec E~\)は関係せず, 面積要素には同じ応力が働くということである。
上述の静電応力テンソルの議論を, (10)式右辺, 積分の中の磁場\(~\Vec B~\)の項にも適用すると, 磁気部分の応力テンソルが得られる。\(\Vec E~\)を\(~\Vec B~\)に換え, \(\varepsilon~\)を\(~1/\mu\)に換えれば良い。電場および磁場が存在する場合の応力テンソルは, 静電応力テンソルと磁気応力テンソルの和として,
\[\Vec T=\Vec T_e+\Vec T_m\]
のように表される。ただし,
\[
\Vec T_e=\varepsilon_0
\begin{pmatrix}
E^2_x-\frac{1}{2}\Vec E^2 & E_xE_y & E_xE_z \\
E_yE_x & E^2_y-\frac{1}{2}\Vec E^2 & E_yE_z \\
E_zE_x & E_zE_y & E^2_z-\frac{1}{2}\Vec E^2
\end{pmatrix}
\]
\[
\Vec T_m=\frac{1}{\mu_0}
\begin{pmatrix}
B^2_x-\frac{1}{2}\Vec B^2 & B_xB_y & B_xB_z \\
B_yB_x & B^2_y-\frac{1}{2}\Vec B^2 & B_yB_z \\
B_zB_x & B_zE_y &B^2_z-\frac{1}{2}\Vec B^2
\end{pmatrix}
\]
である。応力に関して, 電場と磁場は独立に働くのが面白い。
運動量保存則 ファインマンのパラドックスは解決できるか?
電磁場の運動量 ポインティング・ベクトル再び登場
電磁波の運動量で示唆される, 電磁波によって運ばれる運動量の正体が少しづつ明らかになってきた。(10)式を再掲しよう。
\[
\frac{d}{dt}\left(\Vec P_{粒子}+\int_V \varepsilon_0(\Vec E\x \Vec B)dV \right)
=\int_V \left[\varepsilon_0(\Vec E div\Vec E-\Vec E\x rot\Vec E)+\frac{1}
{\mu_0}(\Vec B div\Vec B-\Vec B\x rot\Vec B)\right]\,dV \tag{10}
\]
右辺の被積分の項は「応力テンソル」と呼ばれ, 単位体積当たりの電荷に働く力であることが分かった。
左辺第1項は粒子の力学的運動量である。すると第2項も運動量と同列に数えられる何らかの量であり, 電場や磁場で表されているから, これを電磁場の運動量を呼んでも良いであろう。実際積分の被積分項はポインティング・ベクトルであり, 電磁波の進む方向を表している。
もし考えている系の外部に電荷が無く(従って電流もなく)外部からの電磁場もない場合, (10)式の右辺はゼロとなる。従ってその系は以下の運動量保存則を満たすようにふるまう。
\[\frac{d}{dt}(\Vec P_{粒子}+\Vec P_{field})=0 \]
ここで\(~\Vec P_{field}~\)は新しく導入された運動量で, \(~\displaystyle \Vec P_{field}=\int_V \varepsilon_0(\Vec E\x \Vec B)dV~\)である。
「ファインマンのパラドックス」で述べた荷電粒子の奇妙な振る舞いはこのために起こる。荷電粒子は一見作用反作用の法則を破るような運動をするが,
電磁場の運動量まで考えると運動量の保存則は破られていない。
平面波が運ぶ運動量 \(E=mc^2~\)の芽がこんなところに!
ここで運動量密度\(~\bm{g}~\)を定義しよう。\(~\displaystyle \int_V \varepsilon_0(\Vec E\x \Vec B)dV=\int_V \frac{1}{c^2}(\Vec E\x \Vec H)dV~\)が新しい運動量であるから,
\[\bm{g}=\frac{1}{c^2}(\Vec E\x \Vec H)\quad[\Vec J\cdot s/m^4] \tag{27}\]
を(電磁場の)運動量密度とするのは自然だろう。\(\Vec E\x \Vec H~\)はポインティング・ベクトルである。今までと表記が異なるが, 歴史的にはこちらが先であり, \(\Vec E,\,\Vec B~\)系を採用する場合でも, ポインティング・ベクトルだけは, \(\Vec E\x \Vec H~\)とする場合が多いようである。
なを, (27)式の関係, すなわち 運動量密度=(エネルギー流れ密度)/\(c^2\)は, 電磁気に限らず, ビリヤード球がぶつかる場合でも成り立つ。電磁波が速度\(~c~\)で進むからという分けではない。(ファインマン物理学IV p91)
一例を示す。単位体積に\(~N~\)個の粒子があり, これらが速度\(~\bm{\upsilon}~\)で動いているとする。単位面積を1秒間に通過するエネルギーは, 面を1秒間に通過する粒子数\(~N\upsilon~\)に各粒子のエネルギーをかけたものである。各粒子のエネルギーは\(~m_0c^2/\sqrt{1-\upsilon^2/c^2}~\)であるから, 1秒間のエネルギーの流れは
\[N\upsilon \frac{m_0c^2}{\sqrt{1-\upsilon^2/c^2}}\]
となる。各粒子の運動量は\(~m_0\upsilon/\sqrt{1-\upsilon^2/c^2}~\)であるから, 運動量密度は
\[N \frac{m_0\upsilon}{\sqrt{1-\upsilon^2/c^2}}\]
となり, エネルギーの流れの\(~1/c^2~\)倍に等しい。
話を元に戻そう。ポインティング・ベクトルは「エネルギー流れ密度(電流密度に置換えて考えると分かりやすい)」だから, 単位時間に単位面積を通過するエネルギー量である。エネルギー密度を\(~u~\)とすると, \(u~\)に光速\(~c~\)をかけたものが単位時間に単位面積を通過するエネルギー量だから,
\[uc=|\Vec E\x \Vec H| \]
である。\(\displaystyle \bm{g}=\frac{1}{c^2}(\Vec E\x \Vec H)~\)と比べて
\[u=c|\bm{g}| \]
の関係がある事が分かる。光子はエネルギー\(~E~\)と運動量\(~\bm{p}~\)を持つ粒子であり,
\[E=c|\bm{p}|\]
は, どこかで見たことがあるだろう。
ポアンカレは, エネルギー\(~E~\)と運動量\(~p~\)を持つ光の波束を考え, ポインティングの考え\(~E=c\,p~\)に従って, 非相対論的なニュートンの関係式\(~p=m\upsilon~\)を適用して, エネルギー\(~E~\)の光束は質量\(~m=E/c^2~\)を持つ, つまり
\[E=mc^2\]
であると考えていたようである。
電磁波の持つ運動量とエネルギーの間の上の関係式は, 電磁場の量子化によって出てくる光子のエネルギーが\(~h\nu\), 運動量が\(~h\nu/c~\)であることに対応している。また相対論的なエネルギーと運動量の関係式,
\[E^2=p^2c^2+(mc^2)^2\]
において, 質量がゼロの場合の運動量とエネルギーの間の関係式
\[p=\frac{E}{c}\]
にも対応している。電磁波の運動量という概念は, 相対論的な新しい概念, すなわち, 質量がなくてもエネルギーに伴って運動量が現れることを示唆していた分けである。
高校物理の最後の章で, 光子のエネルギー\(~E=h\nu~\)とか, 運動量\(\displaystyle~p=\frac{h}{\lambda}=\frac{h\nu}{c}~\)だとかが唐突に出てきて戸惑った記憶のある読者も多いのではなかろうか?
相対論まで行かずとも, 電磁気学の範囲で得られた結果だったのだ。
電磁波は運動量を運ぶ
電磁波が運動量を持つ証拠はミクロの世界では観測されており, 例えばコンプトン効果は光と運動量の保存によるものと解釈される。天体現象では, 彗星の尾が反対方向に流されるが, これは太陽からくる光の圧力によるものと考えられている。
最近, 光が\(~p~\)で表される線形運動量だけではなく, 回転運動にまつわる運動量, すなわち軌道角運動量を持ちうることが見いだされ, 「光渦\(~(optical vortex)\)」として研究されている。光渦はその軌道角運動量を物体に移送することで物体に回転運動を与えることが確かめられ, 回転運動を与える光ピンセットとして応用されている。また, 光渦の軌道角運動量の自由度を量子ビットとして利用した情報通信への応用も研究されている。