角運動量保存則
向心力を受けて運動する物体の角運動量 まずは証明してしまおう。
位置\(~\bm{r}~\)において, 運動量 \(~\bm{p}~\)を持つ質点の原点まわりの角運動量\(~\Vec L~\)を
\[\Vec L≡\bm{r}\x \bm{p} \tag{1} \]
と定義する。
質量\(~m~\)の質点が中心力\(~\Vec F~\)を受けて運動しているとする。(1)の両辺を時間\(~t~\)で微分すると,
\[\begin{align}
\frac{d\Vec L}{dt}&=\frac{d}{dt}(\bm{r}\x \bm{p}) \\
&=\frac{d\bm{r}}{dt}\x \bm{p}+\bm{r}\x \frac{d\bm{p}}{dt} \tag{2} \\
&=\bm{\upsilon}\x m\bm{\upsilon}+\bm{r}\x \Vec F \tag{3} \\
&=\bm{0}+ \bm{0}\\
\end{align}\]
となり, 角運動量保存則が示される。(3)式の第1項は\(~\bm{\upsilon}~\)と\(~\bm{\upsilon}~\)が同じ向き。第2項は\(~\bm{r}~\)と\(~\Vec F~\)が平行(逆方向)なので, ともに外積は\(~0~\)。
とまあ, 何ともエレガントというか, カッコいいというか証明は終わりである。
途中 \(~\bm{r}\x \Vec F~ \)を力のモーメント\(~\Vec N= \bm{r}\x \Vec F~ \)として, 外力\(~\Vec N~\)が\(~0~\)の時, 角運動量が保存されるという方が一般的ではある。
ここで注目すべきは(2)式第1項の\(~d\bm{r}/dt~\)である。\(~\bm{r}~\)の向きだけではなく, 大きさが変化しても, 保存則は成り立つ。
我々は, 角運動量\(~r\x p~\)を考える時, \(~r~\)が一定の円運動を想い浮かべていないだろうか?
角運動量(正確には角速度)をベクトルとして取り扱ってよいという数学的根拠は, このような状況をも表現し得る。ちょっとした驚きである。このことについては, 後でまた触れる。
とは言っても,
角運動量ベクトルには, 方向等の実体は無く,
擬ベクトルという称号を得ている。
実体の無いベクトルの数式変形だけではどこか素直になれない。
もう少し物理現象が見える形で考えてみよう。
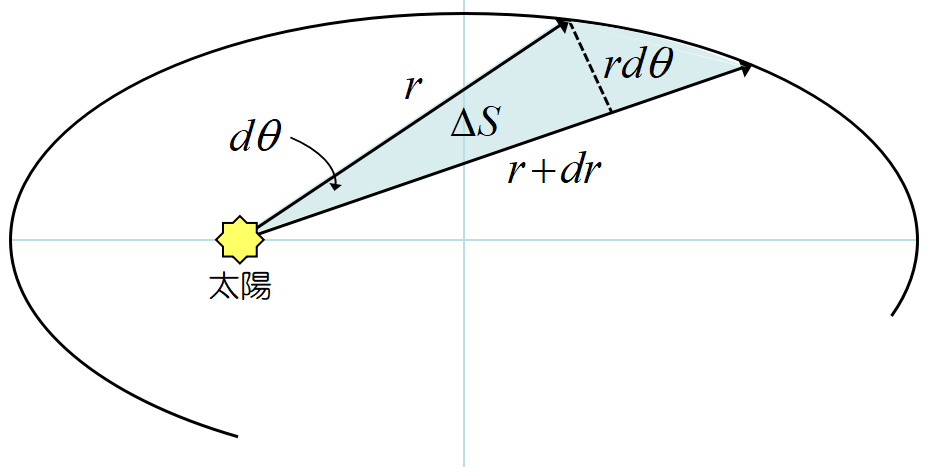
面積速度一定
ケプラーの法則より, 向心力を受けた物体の運動は面積速度が一定となる。
動径角が\(~d \theta~\)変化した時の面積の変化を\(\triangle S\)とすると,
\[\begin{align}
\triangle S &= \frac{1}{2}(r+dr)r d\theta \\
&= \frac{1}{2}(r^2 d\theta + r dr d\theta) \\
&= \frac{1}{2} r^2 d\theta \tag{4} \\
\end{align}\]
と表される。\(dr d\theta~\)の項は落とした。角速度を\(~\omega~ \)とすると\(~d\theta = \omega dt~\)だから, (4)式に代入して両辺を\(~dt~\)で割ると, 面積速度は
\[\frac{\triangle S}{dt}= \frac{1}{2} r^2 \omega = \frac{1}{2} r\x r\omega
= \frac{1}{2} r \upsilon \tag{5} \]
これが一定であるから, (5)式に質量\(~m~\)を掛けて2倍した
\[L=mr\upsilon=rm\upsilon=rp\]
は一定である。ここに\(~p~\)は質点の運動量である。動径\(~r~\)と運動量\(~p~\)の積が角運動量だから, 上式は角運動量保存則を表している。
途中(3)式で出てきた「力のモーメント」について説明をしておこう。
力のモーメント
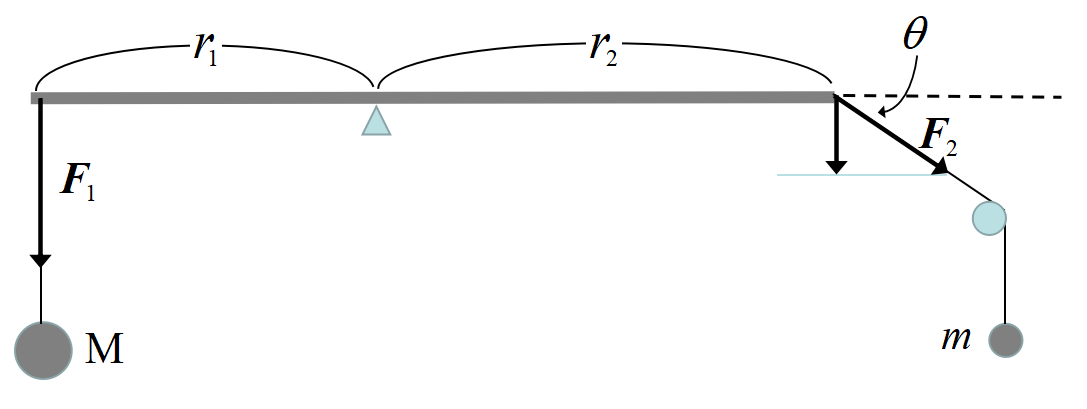
力のモーメント:回転させる力 実は小学校で習っている。
小学校6年の理科の教科書に, 腕の長さと重りの重さを掛けた値が等しいとき, 天秤が釣り合うとある。
図で天秤が釣り合っていると,
\[r_1 \x F_1= r_2 \x F_2 sin \theta \]
が成り立つ。小学校では\(~sin~\)は習わないが, バランスに有効な力は棒に垂直な成分である。中学受験の子供たちは知っている。
\[N = r\x Fsin\theta \]
を, 棒を回転させようとする力とすることには異論はないだろう。\(~sin\theta~\)が入っているから, 外積で表すのが便利だ。
\[\Vec N= \bm{r}\x \Vec F\]
として,
力のモーメントあるいは
トルクと呼ぶ。
「トルク」は一定の力で締め付ける「トルクレンチ」等日常語であるが, 何か全く新しい物理量であるかのような解説が多い。
(3)式を
\[\frac{d\Vec L}{dt} = \Vec N= \bm{r}\x \Vec F \tag{6} \]
と書き直すと,
単位時間当たりの角運動量の変化=回転させる力と言える。
そういえば, 運動方程式は
単位時間当たりの運動量の変化=併進させる力であった。併進運動の運動量と, 回転運動の角運動量には類似点がありそうである。
慣性モーメント
併進運動と回転運動のアナロジーをさらに進めよう。
併進運動の速度\(~\bm{\upsilon}~\)に対応する物理量として, 回転の速度を角速度ベクトル
\[~\bm{\omega} = \bm{n} d\phi /dt~\]
として, 運動量\(~\bm{p}=m\bm{\upsilon}~\)に対して, 角運動量を
\[\Vec L =I \bm{\omega} \tag{7}\]
という形で表してみたい。ここに\(~\bm{n}~\)は, 回転軸方向の単位ベクトルである。
\[\begin{align}
\Vec L &=\bm{r}\x \bm{p} \\
&=\bm{r}\x m\bm{\upsilon} \\
&=\bm{r}\x m\x r \bm{\omega} \\
&= mr^2\omega \tag{8} \\
\end{align} \]
(7)式と比べて, \(~I~\)を
\[I= mr^2\]
とすると辻褄があう。\(~I~\)を
慣性モーメントと呼ぶ。
慣性モーメントとは分かり難い言葉である。モーメントは恐らく\(~momentum~\)から来ており, 元々は, 弾み, 勢い, 推進力といった意味らしい。運動量は\(~momentum~\)の訳語である。回転のモーメントというと何となく分かるが, 大きな慣性モーメント, 慣性の勢いが大きいと言えば, 中々止まらない, 中々動き出さないといった意味合いであろうか? 英語圏で育った人はどのような感じを受けるのだろうか?
円板の慣性モーメント 一度は計算してみよう。
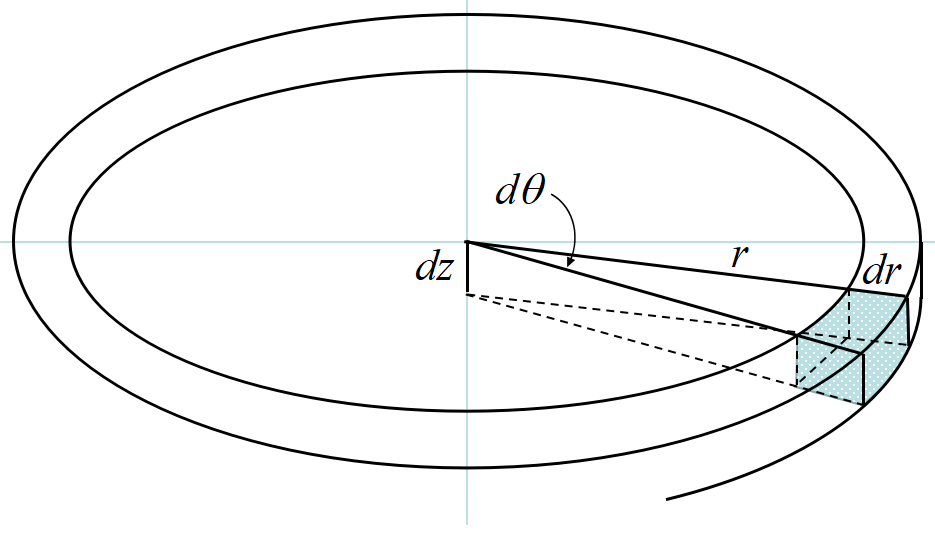
半径\(~a~\), 厚さ\(~b~\), 密度\(~\rho~\)の均一な円板を例に取って説明しよう。この場合は円筒座標が便利である。
図の微小分の質量は, 縦\(~dr~\), 横\(~rd \theta\), 高さ\(~dz~\)の直方体と考えて良いから,
\[dm= \rho \ dr r d\theta dz \]
従って全体の慣性モーメント\(~I~\)は
\[\begin{align}
I&= \int_{0}^{a} \int_{0}^{2 \pi} \int_{0}^{b} \rho dr r d\theta dz \cdot r^2 \\
&= \rho\ 2\pi b \left[\frac{1}{4}{r^4}\right]^a_0 \\
&= \frac{1}{2} \rho\ \pi a^2 b a^2 \\
&= \frac{1}{2} M a^2 \tag{9} \\
\end{align}\]
\(M=\rho \ 2\pi a^2 b~\)は全質量である。同じ半径ならば質量が大きい方が, また同じ質量ならば半径の大きい方が回しにくい。納得できるであろう。
球面座標の方が便利な時は\(~dm=\rho r^2 sin\theta drd\theta d\phi\)として計算すれば良い。
円板の回転の運動エネルギー
\(dm\)部分の運動エネルギー\(~dK~\)は, \(\upsilon= r\omega~\)より,
\[dK=\frac{1}{2}(\rho \ dr r d\theta dz)(r\omega)^2 \]
だから, 円板の全運動エネルギーは
\[\begin{align}
K&=\int_{0}^{a} \int_{0}^{2 \pi} \int_{0}^{b} \frac{1}{2}(\rho \ dr r d\theta dz)
(r\omega)^2 \\
&=\frac{1}{2}\rho \cdot 2\pi b \int_{0}^{a} r^3 \omega ^2 \ dr \\
&=\rho \pi b \left[\frac{1}{4}{r^4}\right]^a_0 \omega^2 \\
&=\frac{1}{4}\rho \pi a^2 b\cdot a^2 \omega^2 \\
&=\frac{1}{2}Ma^2\cdot\frac{1}{2}\omega^2 \\
&=\frac{1}{2}I\omega^2 \\
\end{align}\]
である、ここで今まで出てきた用語を整理しよう。
併進運動と回転運動対比
| 併進運動 | 回転運動 |
| \((速度)\ \bm{\upsilon}\) | \((角速度)\ \bm{\omega}\) |
| \((動き難さ)\ m \) | \((慣性モーメント)\ I\) |
| \((運動の勢い)\ \bm{p}=m\bm{\upsilon}\) | \((回転の勢い)\ \Vec L=\bm{r}\x \bm{p}=I \bm{\omega}\) |
| \(\displaystyle(力)\ \frac{d\bm{p}}{dt}=\Vec F\) | \(\displaystyle(トルク)\ \frac{d\Vec L}{dt}=\Vec N= \bm{r}\x \Vec F\) |
| \(\displaystyle(運動方程式)\ m\frac{d\bm{\upsilon}}{dt}=\Vec F\) | \(\displaystyle(回転方程式)\ I\frac{d\bm{\omega}}{dt}=\Vec N \) |
| \(\displaystyle(運動エネルギー)\ \frac{1}{2}m\upsilon^2 \) | \(\displaystyle(回転エネルギー)\ \frac{1}{2}I\omega^2 \) |
(回転方程式, 回転エネルギーは筆者の造語です)
これまでの議論だと, 慣性モーメントは併進運動における質量のような, スカラー量に思える。
はたしてこれで良いのだろうか?もう少し検討してみよう。
角運動量ベクトルと角速度ベクトルを
\[~\Vec L= \Vec L(L_x,L_y,L_z) \]
\[~\bm{\omega}= \bm{\omega}(\omega_x,\omega_y,\omega_z) \]
とすると,
\[L_x=I_x \omega_x,\ L_y=I_y \omega_y,\ L_z=I_z \omega_z \tag{10}\]
だろうから, (7)式の\(\Vec L =I \bm{\omega}~\)は
\[\begin{align}
\begin{pmatrix}
L_x \\
L_y \\
L_z \\
\end{pmatrix} =
\begin{pmatrix}
I_x & 0 & 0 \\
0 & I_y & 0 \\
0 & 0 & I_z \\
\end{pmatrix}
\begin{pmatrix}
\omega_x \\
\omega_y \\
\omega_z \\
\end{pmatrix} \tag{11}
\end{align}\]
と綺麗な形で表せる。本当にこれで良いのだろうか?半径\(~a~\), 厚さ\(~d~\)の円板の回転について考えてみよう。
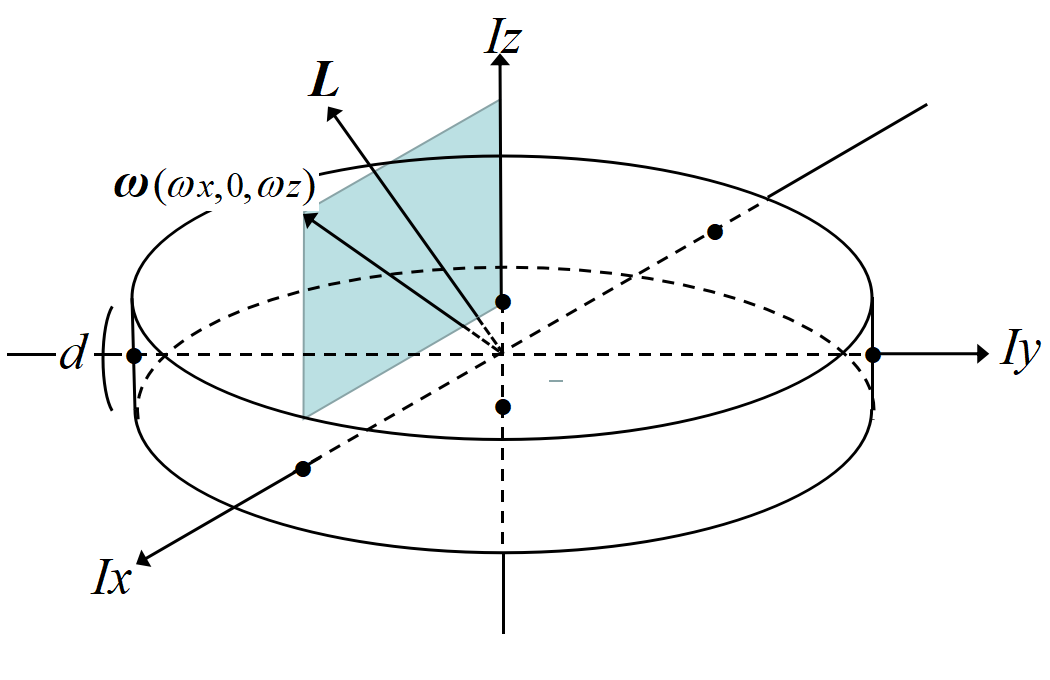
図の慣性モーメント\(I_z\)は(9)式から, \(I_x\),\(I_y\)は同様な計算または直交軸の定理から,
\[I_x=\frac{1}{4}Ma^2\]
\[I_y=\frac{1}{4}Ma^2\]
\[I_z=\frac{1}{2}Ma^2\]
である。\(\Vec L=\Vec I \bm{\omega}~\)を\((\omega_x,\omega_y,0)\)という回転軸で計算してみると,
\[\Vec L= \Vec L\left(\frac{1}{4}Ma^2\omega_x,\frac{1}{4}Ma^2\omega_y,0 \right)\]
と, 良さそうであるが, \((\omega_x,0, \omega_z)\)では
\[\Vec L= \Vec L\left(\frac{1}{4}Ma^2\omega_x, 0 ,\frac{1}{2}Ma^2\omega_z\right)\]
となり, \(~\bm{\omega}~\)と,\(~\Vec L~\)の方向が異なり, 角運動量が実際に回転している軸方向以外を向いてしまう。これは変だ!
(11)式は\(~\bm{\omega}~\)が\(~(\omega_x,0,0)\)とか, \(~(0,0,\omega_z)\)のように座標軸と一致するときにのみ当てはまるようだ。改めて
\[\Vec L= I\bm{\omega}\]
を注意深く考えよう。\(~\Vec L~\)と\(~\bm{\omega}~\)は物理的に異なるベクトルであって, 違った次元を持つ。
慣性モーメントも回転の演算子(無次元)とは異なり, 次元(\(質量 \x 長さ^2\))を持つ。やはり単純に運動量とは比較できない。
角運動量は実体の無いベクトルとはいえ, 数学者がベクトルとして取り扱って良いとのお墨付きを与えてくれている。(7)式のように安易に考えるのではなく, 数学者を信じて慎重に変形して行こう。
質点が複数ある場合を考えると,
\[\Vec L=m_i(\bm{r}_i \x \bm{\upsilon}_i) \tag{12} \]
ここで\(~\bm{r}_i~\)及び\(~\bm{\upsilon}_i~\)はそれぞれ, 固定点からみた\(~i~\)番目の粒子の動径ベクトルおよび速度である。\(~\bm{\upsilon}_i= \bm{\omega}\x \bm{r}_i~ \)を(12)式に代入して,
\[\Vec L= m_i[\bm{r}_i\x (\bm{\omega}\x \bm{r}_i)] \tag{13} \]
を得る。このベクトル3重積を展開すると(有名な公式がある),
\[\Vec L= m_i[\bm{\omega}r_i^2- \bm{r}_i(\bm{r}_i\cdot \bm{\omega})]\]
さらにスカラー積も展開すると, 角運動量の\(~x~\)成分\(~L_x~\)は
\[L_x= \omega_x m_i(r_i^2-x_i^2)-\omega_y m_i x_i y_i- \omega_z m_i x_i z_i \]
となる。\(r_i^2= x_i^2+ y_i^2+ z_i^2~ \)を使って書き直すと,
\[L_x= +\omega_x m_i(y_i^2+z_i^2)-\omega_y m_i x_i y_i- \omega_z m_i x_i z_i \]
\[L_y= -\omega_x m_i y_i x_i+ \omega_y m_i(z_i^2+x_i^2)-\omega_z m_i y_i z_i \]
\[L_z= -\omega_x m_i z_i x_i- \omega_y m_i z_i y_i +\omega_z m_i(x_i^2+y_i^2)\]
\(~L_y,L_z~\)も書き出した。\(\omega_y m_i x_i y_i\)等は, 同じ添え字が出てきた時は, 全て足し上げるアインシュタインの規約である。まとめて,
\[\begin{align}
\Vec L &=
\begin{pmatrix}
L_x \\
L_y \\
L_z \\
\end{pmatrix} \\
&=
\begin{pmatrix}
m_i(y_i^2+z_i^2) & -m_iy_iz_i & -m_iz_ix_i \\
-m_ix_iy_i & m_i(z_i^2+x_i^2) & -m_iz_iy_i \\
-m_ix_iz_i & -m_iy_iz_i & m_i(x_i^2+y_i^2) \\
\end{pmatrix}
\begin{pmatrix}
\omega_x \\
\omega_y \\
\omega_z \\
\end{pmatrix} \\
&=
\begin{pmatrix}
I_{xx} & I_{xy} & I_{xz} \\
I_{yx} & I_{yy} & I_{yz} \\
I_{zx} & I_{zy} & I_{zz} \\
\end{pmatrix}
\begin{pmatrix}
\omega_x \\
\omega_y \\
\omega_z \\
\end{pmatrix} \tag{14}\\
&=\Vec I \bm{\omega} \tag{15}
\end{align}\]
となる。対角成分は今まで説明してきた
慣性モーメント, 非対角成分は
慣性乗積と呼ぶ。
剛体が\(~I_x, I_y, I_z~\)といった主軸の回りを回転しているときは, 慣性モーメントしか現れない。(11)式は主軸のみの特別な場合であったわけだ。
慣性乗積は回転が主軸からずれた時の, 回転のしにくさを反映し, 歳差運動と深い関係がある。
そしてこの主軸からのずれによる影響の実測値は, 慣性乗積とピタリと合う。数学者がここまで考えたかどうかは分からないが, 大したものである。
いい加減な角運動量の定義は以下のようなものだろうか。
角運動量は動径の大きさと, 動径に垂直な運動量の成分を掛ける。この時\(~sin\theta~\)が出てきて丁度良いので外積にしてしまおう。
こんな軽いノリで
定義したとしたら, 慣性乗積のような信頼のおける結果はとても導き出せないであろう。
さて行列\(~\Vec I~\)の意味をもう少し考えてみよう。(14)式の一部を書き出すと,
\[L_x=I_{xx}\omega_x+ I_{xy}\omega_y +I_{xz}\omega_z \]
であるから, 角運動量の各成分は角速度ベクトルの全ての成分の1次関数である。
言い換えると角運動量ベクトルは角速度と1次変換で関係づけられている。
1次変換の演算子には, 座標変換と, ベクトル\(~\bm{r}~\)に作用して別のベクトル\(~\bm{r'}~\)に変換させる2通りの作用がある。\(~I~\)は明らかに後者である。
\(~\Vec L~\)と\(~\bm{\omega}~\)は物理的に異なるベクトルであって, 違った次元を持ち, 単に同じベクトルを2つの異なった座標系で表したものではない。
\(\Vec L= \Vec I\bm{\omega}~\)はベクトル\(~\bm{\omega}~\)に\(~\Vec I~\)を作用させると, 物理的に異なったベクトル\(~\Vec L~\)が得られると解釈すべきである。
(14)式の行列\(~\Vec I~\)が\(~\Vec L~\)と\(~\bm{\omega}~\)の関係を正しく結ぶものである。
ベクトルでも単なる行列でもないので, これを
慣性モーメントテンソルあるいは略して
慣性テンソルと呼ぶ。
これ以降は慣性モーメントテンソルは\(~\Vec I~\)ではなく, \(~\tilde{\Vec I}\)と書くこととしよう。
さて, もう少し異なった分野での例を考えてみよう。
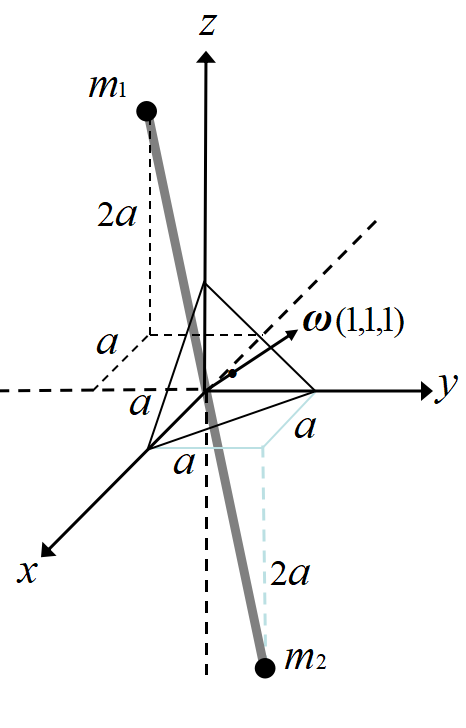
質量\(~m_1,m_2\)の2つの原子が, それぞれ\((-a,-a,2a),(a,a,-2a)\)の位置にあり, 強い力で結びついているとする。お互いの距離は不変とする。慣性モーメントテンソル\(~\tilde{\Vec I}\)は
\[\begin{align}
\tilde{\Vec I} &=
\begin{pmatrix}
I_{xx} & I_{xy} & I_{xz} \\
I_{yx} & I_{yy} & I_{yz} \\
I_{zx} & I_{zy} & I_{zz} \\
\end{pmatrix} \\
&=
\begin{pmatrix}
m_i(y_i^2+z_i^2) & -m_iy_iz_i & -m_iz_ix_i \\
-m_ix_iy_i & m_i(z_i^2+x_i^2) & -m_iz_iy_i \\
-m_ix_iz_i & -m_iy_iz_i & m_i(x_i^2+y_i^2) \\
\end{pmatrix} \\
&=
\begin{pmatrix}
5Ma^2 & -Ma^2 & 2Ma^2 \\
-Ma^2 & 5Ma^2 & 2Ma^2 \\
2Ma^2 & 2Ma^2 & 2Ma^2 \\
\tag{16}
\end{pmatrix}
\end{align}\]
ここで, \(M=m_1+m_2\)である。\(I_{xx}=5Ma^2\)は
\[~m_1(y_1^2+z_1^2)+ ~m_2(y_2^2+z_2^2)=m_1((-a)^2+(2a)^2)+m_2(a^2+(-2a)^2)=5Ma^2\]
等である。
(16)式の慣性モーメントテンソルはデカルト座標軸に対するものである。このテンソルの固有値と固有ベクトルを求め, 固有ベクトルを並べた直交行列を用いると, 対角化できる。
対角化の計算は本題では無いので結果だけを記すが, 対角化の意味に触れておく。
ベクトルに行列を作用させると, そのベクトルは伸縮, 回転, 平行移動を行う。この時, 特別な行列を用いると, 伸縮はするが向きは変わらないベクトル(固有ベクトル)が得られる。この特定の方向の際立った特徴(固有値)が抽出されて, 行列の対角成分にずらりと並ぶ。すなわち行列の対角化とは, その行列の際立った特徴をあぶりだすことである。
(16)式の慣性モーメントテンソルを対角化すると
\[
\tilde{\Vec I} =
\begin{pmatrix}
0 & 0 & 0 \\
0 & 6Ma^2 & 0 \\
0 & 0 & 6Ma^2
\end{pmatrix} \tag{17}
\]
となる。対角成分\(~I_1=0,I_2=6Ma^2,I_3=6Ma^2~\)を主慣性モーメントと呼ぶ。
\(~I_1\)は\(~(1,1,-2)~\)方向を回転軸(慣性主軸)とする慣性モーメントである。\(~(1,1,-2)~\)方向は2つの原子を結ぶ直線で, この直線を軸とするときは力のモーメントはゼロである。原子\(~m_1, m_2 ~\)はスピンのみで, 軌道角運動量はゼロである。
\(~I_2\)は\(~(1,-1,0)~\)方向を回転軸(慣性主軸)とする慣性モーメントである。ベクトル\(~(1,1,-2)~\)とベクトル\(~(1,-1,0)~\)は内積が\(~0~\)から分かるように, 原子を結ぶ軸に垂直である。
2つの重りを結び付けた棒の中心を持ち, 棒を水平に回転させる時が回りにくいのは感覚的に分かるであろう。
\(~(1,1,1)~\)方向も2つの原子を結ぶ軸に垂直で, \(~I_3\)は, \(~(1,1,1)~\)を主軸とする慣性モーメントである。
例えば角速度\(~\omega~\)の時, \(~(1,1,1)~\)軸周りの角運動量は,
\[\Vec L=I_3\ \omega= 6Ma^2\ \omega
\begin{pmatrix}
1 \\
1 \\
1 \\
\end{pmatrix} \]
と表される。
テンソルと行列は異なるものであるという説明をよく見かける。実際, 上の例で見たように慣性モーメントテンソルは次元を持っているのに, 単なる回転行列は無次元である。しかしこの区別を過度にすることは, 却ってテンソルの理解を妨げる。直交変換という限られた領域では,2階のテンソルとその成分によって作られる正方行列は実際同じように取り扱われる。実際のテンソル方程式にも, それぞれ1つの行列方程式が対応し, その逆も成り立つ。
"転置"や"反対称"のような行列代数の用語や操作は何の変更もせずに, テンソルに適用することが出来る。
一般相対論では, 多くの挑戦者がテンソルで打ちのめされる。今はあまり厳密な数理に捕らわれずに, 多くの計算を通して感覚的に身に着ける方が良いように思われる。筆者も「変換性」,「多重線形性」,「テンソル積」等随分と遠回りをした。