コンデンサー内部に働く力 受験生はポテンシャルの微分に慣れよう!
コンデンサー内部の力は, クーロンの法則から計算しても良いが, 多くの場合エネルギー保存則, すなわち
\[F_x=-\dd{U}{x}\tag{1}\]
を用いる方が簡単である。それほど難しくないので, 受験生も憶えておいた方が自信を持って試験に臨める。
なおこの記事では\(~F_x~\)は外力を表し, (1)式で求めるのは内部の力\(~F_c~\)であることに注意。
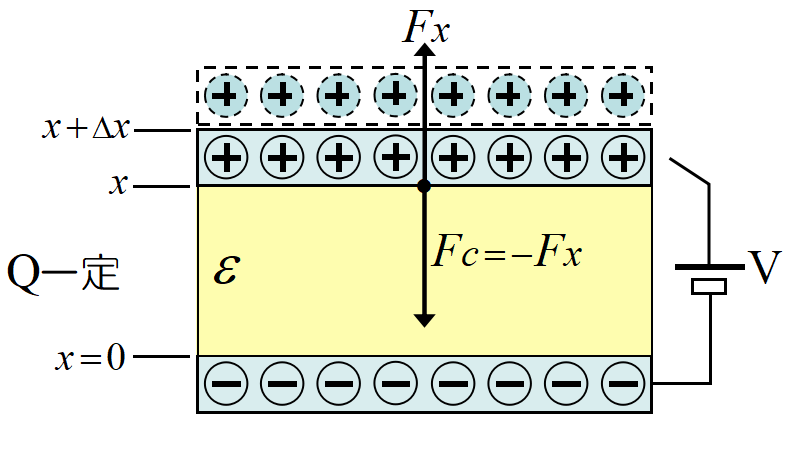
極板の引き合う力(1) 電荷が一定の場合
外部の力とコンデンサー内部の静電気力のみが働く。電池の作用が無く, これが基本。
極板の面積\(~S\), 距離\(~x~\)(普通は\(~d~\)とするが, 記述を統一した)誘電率\(~\varepsilon=\varepsilon_0\varepsilon_r~\)のコンデンサーを考える。
最初電池に繋ぎ, 電荷\(~Q=CV~\)を充電したのち, スイッチをオフにする。
極板の引き合う力を\(~F_c~\), 加える外力を\(~F_x~\)とする。きわめてゆっくり移動するので\(Fx=-F_c~\)である。
静電エネルギー\(~U~\)の表現は次の3通りの方法がある。
\[\begin{align}
U&=\frac{1}{2}QV \tag{2}\\
&=\frac{1}{2}CV^2=\frac{V^2}{2}\frac{\varepsilon S}{x} \tag{3}\\
&=\frac{Q^2}{2C}=\frac{Q^2}{2}\frac{x}{\varepsilon S} \tag{4}
\end{align}\]
ここで注意すべきは(2)式で, 電荷蓄積体が必ずこうなるわけでは無い。一般には
\[U=\int_{0}^{Q}V(Q)dQ\]
である。平行板コンデンサーが\(~Q=CV\), もっと分かり易く言えば\(~V=kQ~\)の形をしているので(2)~(4)になるのである。
(1) 外力を仮定する解法。受験関係の書籍, ネット記事に多い。\(dx~\)は使えないが\(~\triangle x~\)ならば良いのか?
\(Q~\)一定なので, (4)式を用いて
\[\begin{align}
\triangle U&=\frac{Q^2}{2}\triangle\left(\frac{x}{\varepsilon S}\right)\\
&=\frac{Q^2}{2\varepsilon S}\triangle x \tag{5}
\end{align}\]
一方, 外力\(~F_x~\)がした仕事は\(~\triangle W=F_x\x \triangle x~\)で, \(\triangle U=\triangle W\) だから(5)式と比べて
\[F_x=\frac{Q^2}{2\varepsilon S}\]
作用・反作用から
\[F_c=-\frac{Q^2}{2\varepsilon S} \tag{6}\]
-(マイナス)がついているので引力である。引き合うので当然ではある。
(2) 標準解法。外力は不要。 慣れれば最も簡単。受験生にお勧め。
(4)式に(1)式を適用して
\[F_c=-\dd{U}{x}=-\frac{\partial}{\partial x}\left(\frac{Q^2}{2}\frac{x}{\varepsilon S}\right)=-\frac{Q^2}{2\varepsilon S}\]
(6)式と同じ結果が得られた。
(3) 禁じ手。 なぜか解説は見たことが無い。ファインマンの教科書では別の説明になっているが。
コンデンサー内部の電場は
\[E=\frac{Q}{\varepsilon S}\]
である。極板の電荷\(~Q~\)がこの電場から受ける力は
\[F_c=\frac{Q^2}{\varepsilon S}\]
となりそうだが, これは間違い。
内部電場\(~E=Q/\varepsilon S~\)は\(~+Q~\)と\(~-Q~\)の2つの電荷によって形成されたものである。
コンデンサーの静電エネルギー・エネルギー密度。
自身の作った電場に自分の電荷\(~Q~\)をかけてはならない。
それならばこれはどうであろう。例えば単独の極板の作る電場は, 極板の面積が両面で\(~2S~\)だから,
\[E=\frac{Q}{2\varepsilon S}\]
である。この電場にもう一方の極板の電荷\(~Q~\)をかければ
\[F_c=-\frac{Q^2}{2\varepsilon S}\]
で(6)式と同じである。引力であるから-(マイナス)を付け加えた。良さそうな気がするが?
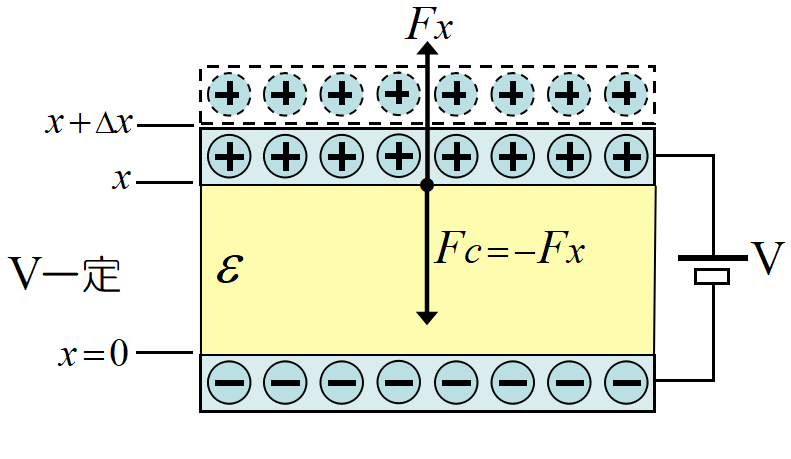
極板の引き合う力(2) 電圧が一定の場合\(~Q~\)一定の時とはかなり異なる挙動を示す。
外部の力とコンデンサー内部の静電気力に加え, 電池が作用するため注意が必要。
電圧\(~V~\)が一定だから, (3)式を使って,
\(\displaystyle F_c=-\dd{U}{x}=+\frac{V^2}{2}\frac{\varepsilon S}{x^2}=+\frac{Q^2}{2}\frac{1}{\varepsilon S}\)
となるが, \(F_c~\)は引力だからこれはおかしい。
(1)式は, 外力によってエネルギーを加え, そのエネルギーが全てその系に蓄えられるとき, すなわち
孤立系において成り立つ。
外部の電池をつなげば, 外力の加えたエネルギーはその電池に溢れ出すかあるいは電池から流入してくる。従ってこの場合(1)式は使えない。
間違いは分かったが, 新しい疑問が起こる。(6)式と符号だけが異なるのは何故だろう? もう少し丁寧に静電エネルギーの変化を考えよう。
(1) 外力を仮定する解法。
\(C,V,Q~\)の組み合わせは種々あるが, 思いつくままに変形してゆくと物理現象が見えなくなる。
辻褄合わせではなく, できるだけ物理変化に沿った形で進めよう。
\[\triangle U=F_x\triangle x+V\triangle Q\tag{7}\]
からスタートする。
左辺はこの系のエネルギー変化, 右辺第1項は外力により与えられるエネルギー, 第2項は電池によって与えられるエネルギーである。
熱力学第1法則に似てなくもない。
\(\triangle Q~\)が正ならばこの系の電荷の増加, 負ならば減少で電荷を電池に戻す。
コンデンサーの容量の変化が重要なので, 先ずここから見てゆく。
\(x \to x+\triangle x~\)となった時の容量の変化(減少)は
\[\triangle C=\triangle \left(\frac{\varepsilon S}{x}\right)=-\frac{\varepsilon S}
{x^2}\triangle x=-C\frac{\triangle x}{x} \tag{8}\]
である。元の容量\(~C~\)の\(~\triangle x/x~\)分だけ減少する。極板の距離が増加し, 容量は減少する。減少幅が\(~\triangle x/x~\)だというので大変分かり易い。
系のエネルギーの変化は電圧一定\(~\triangle V=0~\)を考慮して
\[\triangle U=\triangle \left(\frac{1}{2}CV^2\right)=\frac{V^2}{2}\triangle C =-
\frac{V^2}{2}C\frac{\triangle x}{x}\tag{9} \]
\(\triangle U~\)は負であるから, 外力を加えられたにも拘わらず, 静電エネルギーは減少する。
次に電荷\(~Q~\)の変化を見よう。
\[\triangle Q=\triangle (CV)=V\triangle C=-VC\frac{\triangle x}{x} \tag{10}\]
これも負であるからコンデンサーの電荷は減少する。すなわち電荷を電池に戻す。(9),(10)式を使って(7)式を書き直すと,
\[\begin{align}
F_x\triangle x&=\triangle U-V\triangle Q \\
&=-\frac{V^2}{2}C\frac{\triangle x}{x}+V^2 C\frac{\triangle x}{x}\tag{11}\\
&=+\frac{V^2}{2}C\frac{\triangle x}{x}\\
&=+\frac{Q^2}{2\varepsilon S}\triangle x \tag{12}
\end{align}\]
(12)式より\(~F_x=+Q^2/2\varepsilon S\)。極板間に働く力はその反作用として\(~F_c=-Q^2/2\varepsilon S\)となり, (6)式と同じ結果を得る。
符号が正になってしまうこともない。
電荷, 電圧が同じならば, 電池が繋がっていようといまいと, 極板に働く力は同じだろう。1兆分の1mm動かしたところで変わるはずは無い。
受験生としては(7)~(12)を計算する必要はない。電池が繋がっていても(6)式を答えれば良い。
さて(11)式をみると, コンデンサーのエネルギーの減少分の2倍が電池に戻される。この2倍とか2分の1とかいう記事はよく見かけるが, その理由に言及している例はあまり見ない。
筆者は(12)式よりもこの2倍とか, 絶対値は等しいが符号が逆になる方が気になって, この記事の出稿が相当遅れた。後で触れよう。
(2) 外力を仮定しない解法。
\(\displaystyle F_c=-\frac{\partial}{\partial x}\left(\frac{1}{2}CV^2\right)\)がうまくゆかなかったのは, \(~U~\)に電池を含めなかったからである。電池も含んだエネルギー保存則は
\[F_c\ \triangle x=-\triangle U+V\triangle Q\tag{13}\]
である。左辺は系が外部へする仕事, 具体的には電極支持物体に与えるエネルギーである。
右辺第1項は, 外部への仕事の代価として系が失ったエネルギー, 第2項は電池がコンデンサーに与えたエネルギーである。
\(\triangle U~\)の考え方が(7)式と異なっていることに注意。(7)式では\(~\triangle U~\)の正負は計算の結果に委ねるが, (13)式の\(~\triangle U~\)は正である。(1)式と整合性を取るためである。エネルギーが減少する時は, \(\triangle U\lt 0~\)ではなく, \(-\triangle U~\)とする。
\(~\triangle W~\)とした方が良いかもしれないが, \(~\triangle W~\)を内部エネルギーとしている記事も多い。
\(\triangle Q~\)は(7)式と同じである。正ならば電荷が電池から流入し, 負ならば電荷を電池へ戻すことになる。
(13)式で\(~\triangle x\to 0\)として,
\[\begin{align}
F_c&=-\dd{U}{x}+V\dd{Q}{x} \\
&=-\frac{\partial}{\partial x}\left(\frac{CV^2}{2}\right)+V\dd{(CV)}{x} \\
&=-\frac{V^2}{2}\dd{C}{x}+V^2\dd{C}{x} \tag{14}\\
&=+\frac{V^2}{2}\dd{C}{x} \\
&=-\frac{Q^2}{2\varepsilon S} \\
\end{align}\]
となり, (6)式と同じ値を得る。
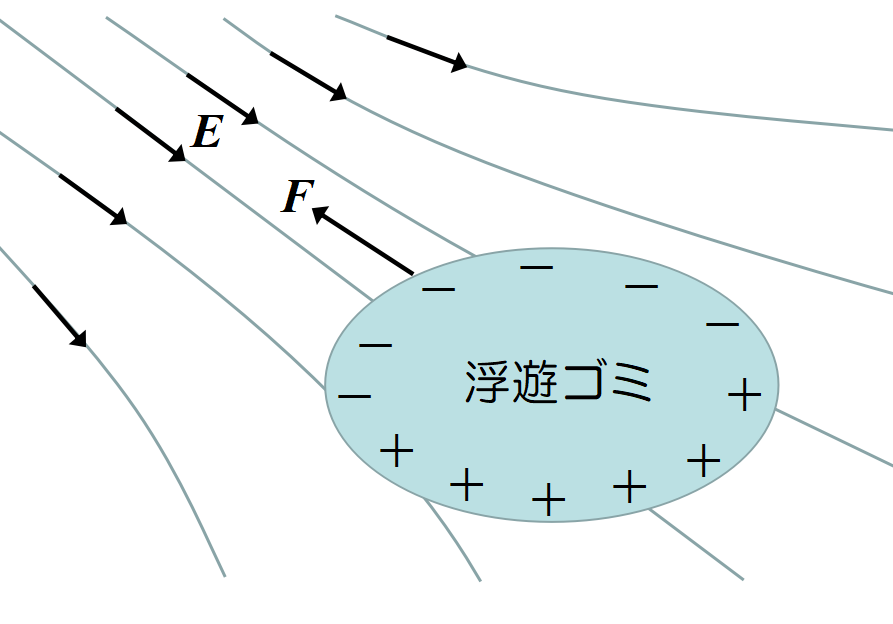
絶縁体がなぜ静電気に引き付けられるのか?
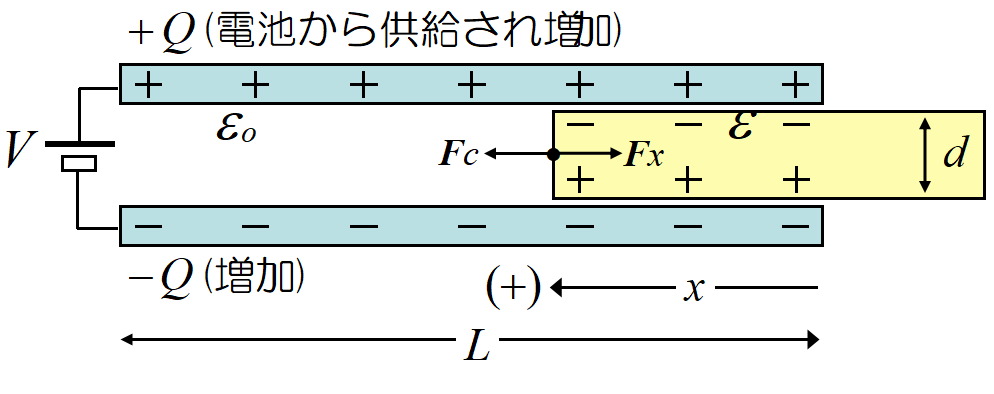
帯電体(プラスチック製品)があるとその周りには電場が発生する。
電場内の絶縁体は誘電分極し, 帯電体との引力が斥力よりわずかに勝り, 常に場の弱い所から強い所へと引かれる。
誘電体(金属でも同じ)はコンデンサーの極板間に引き込まれる。誘電分極(金属の場合は静電誘導)によって現れた電荷が, 極板上の電荷からクーロン力を受けるからである。
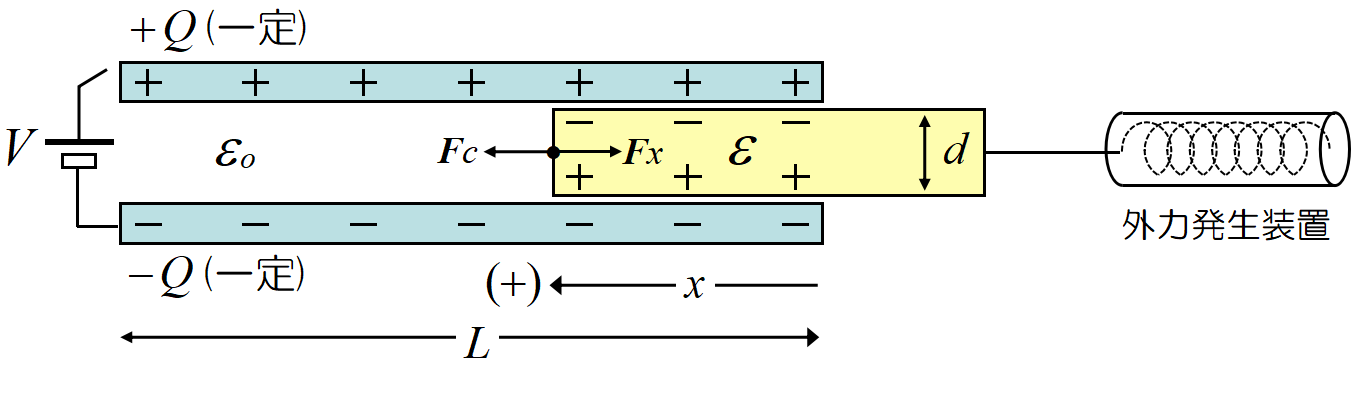
コンデンサーに引き込まれる誘電体(1) 電荷が一定の場合。
外部の力とコンデンサー内部の静電気力のみが働く。電池の作用が無いので簡単。極板間の電位は下がる。
金属板も, 絶縁体も, コンデンサーの極板間に引き込まれる。入試では頻出である。
電場中の双極子モーメントが受ける力が\(~\Vec F=(\bm{p}\cdot\nabla)\Vec E~\)を利用して, 誘電体がコンデンサーに引き込まれる力を直接計算しても求めることは出来る。しかしかなりの技巧と計算量が必要である。
極板の引き合う力と同様, \(\displaystyle F_x=-\dd{U}{x}\)を使った方がずっと簡単な場合が多い。
下図では外力\(~F_x~\)と\(~x~\)軸の向きが逆になっている。まあ, 結果が分かっているのでこの様に取ったが, 極板間の力での説明と異なるので注意。
上図の合成容量は誘電体の無い部分と, 誘電体のある部分の和である。コンデンサーの幅を\(~W~\)とすると合成容量は,
\[\begin{align}
C(x)&=\frac{\varepsilon_0 W(L-x)}{d}+\frac{\varepsilon Wx}{d}\\
&=\frac{W}{d}[\varepsilon_0 L+(\varepsilon-\varepsilon_0)x]\tag{15}\\
\end{align}\]
である。
(1) 外力を仮定する解法。前記同様受験関係の記事に多い。
容量の変化\(~\triangle C~\)は(15)式より
\[\triangle C=\frac{W}{d}(\varepsilon-\varepsilon_0)\triangle x\tag{16}\]
\(\displaystyle U=Q^2/2C\), および(16)式より
\[\begin{align}
\triangle U&=-\frac{1}{2}\frac{Q^2}{C(x)^2}\triangle C \\
&=-\frac{1}{2}\frac{Q^2}{C(x)^2}\frac{W}{d}(\varepsilon-
\varepsilon_0)\triangle x \tag{17} \\
\end{align}\]
これが, 外力がコンデンサーに与えたエネルギー\(~F_x\ \triangle x\)だから(17)式より
\[F_x=-\frac{1}{2}\frac{Q^2}{C(x)^2}\frac{W}{d}(\varepsilon-\varepsilon_0)\]
作用反作用により, \(F_c~\)は反対符号をつけて
\[F_c=+\frac{1}{2}\frac{Q^2}{C(x)^2}\frac{W}{d}(\varepsilon-
\varepsilon_0)\tag{18}\]
(17)式から分かるように, 静電エネルギーは減少する。そのエネルギーは\(F_x=-F_c~\)の外力発生装置に蓄えられる。
記号は+(プラス)なので\(~F_c~\)は\(~x~\)軸と同じ向き, すなわち誘電体を引込む。\(x~\)の項を含むので, 力は一定ではない。
(2) 外力を仮定しない解法。
\(Q~\)が一定なので\(~U=Q^2/2C(x)~\)および(15)式を使って
\[\begin{align}
F_c&=-\dd{U}{x} \\
&=+\frac{1}{2}\frac{Q^2}{C(x)^2}\frac{dC(x)}{dx}\\
&=+\frac{1}{2}\frac{Q^2}{C(x)^2}\frac{W}{d}(\varepsilon -\varepsilon_0) \\
\end{align}\]
で, (18)式と同じ結果が得られる。
コンデンサーに引き込まれる誘電体(2) 電圧が一定の場合
外部の力とコンデンサー内部の静電気力に加え, 電池が作用するため注意が必要。
\(V~\)が一定なので\(~\displaystyle U=\frac{1}{2}CV^2~\)を使って
\(\displaystyle F_c=-\frac{\partial}{\partial x}U=-\frac{\partial}{\partial x}\frac{1}{2}CV^2\)
を計算すると,
\[F_c=-\frac{V^2}{2}\frac{W}{d}(\varepsilon-\varepsilon_0) \tag{20}\]
となる。ー(マイナス)なので, \(~x~\)と反対向き, すなわち誘電体を排出する方向となる。前述したように, 非孤立系に(1)式を適用した間違いである。
ここも
極板の引き合う力(2) 電圧が一定の場合に倣って慎重に分析してみよう。
(1) 外力を仮定する解法。
\[\triangle U=F_x\triangle x+V\triangle Q\tag{21}\]
からスタートする。
左辺はこの系のエネルギー変化, 右辺第1項は外力により与えられるエネルギー, 第2項は電池によって与えられるエネルギーである。
コンデンサーの容量の変化は(16)式より
\[\triangle C(x)=\frac{W}{d}(\varepsilon-\varepsilon_0)\triangle x\tag{22}\]
系のエネルギーの変化は電圧一定\(~\triangle V=0~\)を考慮して
\[\triangle U=\triangle \left(\frac{1}{2}CV^2\right)=\frac{V^2}{2}\frac{W}{d}
(\varepsilon-\varepsilon_0)\triangle x\tag{23} \]
\(\triangle U~\)は正であるから, 静電エネルギーは増加する。次に電荷\(~Q~\)の変化を見よう。
\[\triangle Q=\triangle (CV)=V\triangle C=V\frac{W}{d}(\varepsilon-
\varepsilon_0)\triangle x\tag{24}\]
これも正であるからコンデンサーの電荷は増加する。(23),(24)式を使って(21)式を書き直すと,
\[\begin{align}
F_x\triangle x&=\triangle U-V\triangle Q \\
&=\frac{V^2}{2}\frac{W}{d}(\varepsilon-\varepsilon_0)\triangle x -V^2\frac{W}{d}(\varepsilon-\varepsilon_0)\triangle x \tag{25}\\
&=-\frac{V^2}{2}\frac{W}{d}(\varepsilon-\varepsilon_0)\triangle x
\tag{26}
\end{align}\]
(26)式より\(\displaystyle~F_x=-\frac{V^2}{2}\frac{W}{d}(\varepsilon-\varepsilon_0)\)。誘電体に働く力はこの反作用で
\[\displaystyle~F_c=\frac{V^2}{2}\frac{W}{d}(\varepsilon-\varepsilon_0)\tag{27}\]
となる。記号は+(プラス)なので\(~F_c~\)は\(~x~\)軸と同じ左き, すなわち誘電体を引込む。
静電エネルギーは増加する。誘電率\(~\varepsilon~\)の部分が増えるので当然ではある。\(x~\)の項を含まないので, 力は一定である。
(1) 外力を仮定しない解法。
電池も含んだエネルギー保存則は
\[F_c\ \triangle x=-\triangle U+V\triangle Q\tag{27}\]
である。左辺は系が外部へする仕事, 具体的には電極支持物体に与えるエネルギーである。
右辺第1項は, 外部への仕事の代価として系が失ったエネルギー, 第2項は電池がコンデンサーに与えたエネルギーである。
(27)式で\(~\triangle x\to 0\)として,
\[\begin{align}
F_c&=-\dd{U}{x}+V\dd{Q}{x} \\
&=-\frac{\partial}{\partial x}\left(\frac{CV^2}{2}\right)+V\dd{(CV)}{x} \\
&=-\frac{V^2}{2}\dd{C}{x}+V^2\dd{C}{x} \\
&=+\frac{V^2}{2}\dd{C}{x} \\
&=+\frac{V^2}{2}\frac{W}{d}(\varepsilon-\varepsilon_0)
\end{align}\]
となり, (27)式と同じ値を得る。
さて2倍とか2分の1であるが, 偶然か?答えは
偶然である(と思う)。
(11)式で2倍が表れている。電池からもらう, あるいは電池に戻すエネルギーは\(~Q~\)と\(~V~\)の積で\(~QV~\)である。それに対して静電エネルギーの変化は
\[\triangle U=\triangle \int_{0}^{Q}V(Q)dQ\]
である。平行板コンデンサーの場合は
たまたま\(~V=Q/C~\)の形をしていたので, \(\triangle U=\frac{1}{2}QV~\)となっただけである。
しかし平行板コンデンサーの容量は, ガウスの法則と, \(V=Ed~\)の基本法則から導かれる。
たまたまは言い過ぎではないか?
ガウスの法則によれば電荷\(~Q~\)と, 電場\(~E~\)は1次の関係にある。(\(E=\sqrt{Q}\)のようにはならないということ。)
電位差\(~V~\)は\(~E\x x\)。つまり\(~Q~\)と, 電位差\(~V~\)は1次の関係にある。
それならば,
偶然ではなく, 必然である。
しかし, 全てのエネルギー蓄積体がそうなのか?例外は無いのか?
物理の基本法則は満たしつつ,\(~V=k\ Q~\)の形ではない, 例えば\(V=k\ \sqrt{Q}~\)のようなエネルギー蓄積体は無いかと試行錯誤したが見つからない。無いという証明も出来ない。凡才の限界である。