位置エネルギーはどこに蓄えられるのか?
弾性力位置エネルギー 先ずは最も分かり易い例から
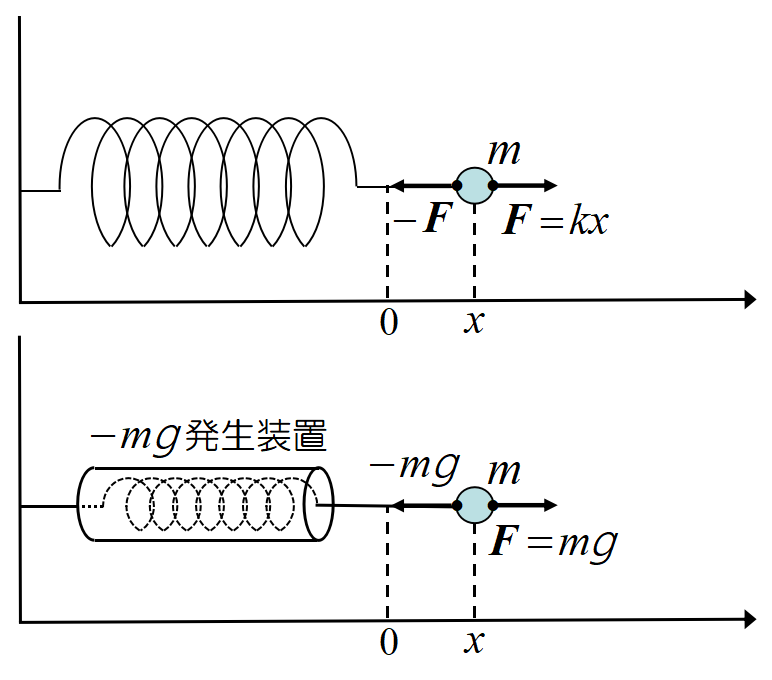
ばねに重りをつけ, 自然長の位置から外力\(~\ F~\)でゆっくり右へ引く。外力は重りに\(~F\cdot\ x~\)のエネルギーを与える。作用反作用により, この時重りは\(~F~\)の力でばねにより左側に引かれる。力の向きと移動方向が反対だから, 重りはばねにより, 外力により与えられたのと同じ量の負のエネルギー(仕事)を与えられる。当然だが重りにエネルギーは蓄えられない。外力が与えたエネルギーはばねが伸びて変形した部分に蓄えられる。
次に\(-mg~\)発生装置を取り付けた重りをゆっくり右に引く。こういう装置が出来るか否かは不明だが, 現代の技術を駆使すればそう難しいことでもあるまい。ばねとは異なり変形する部分が無いが, ばねと同じ推理により, 外力が与えたエネルギーは\(-mg~\)発生装置の内部に蓄えられるであろう。
重力位置エネルギー
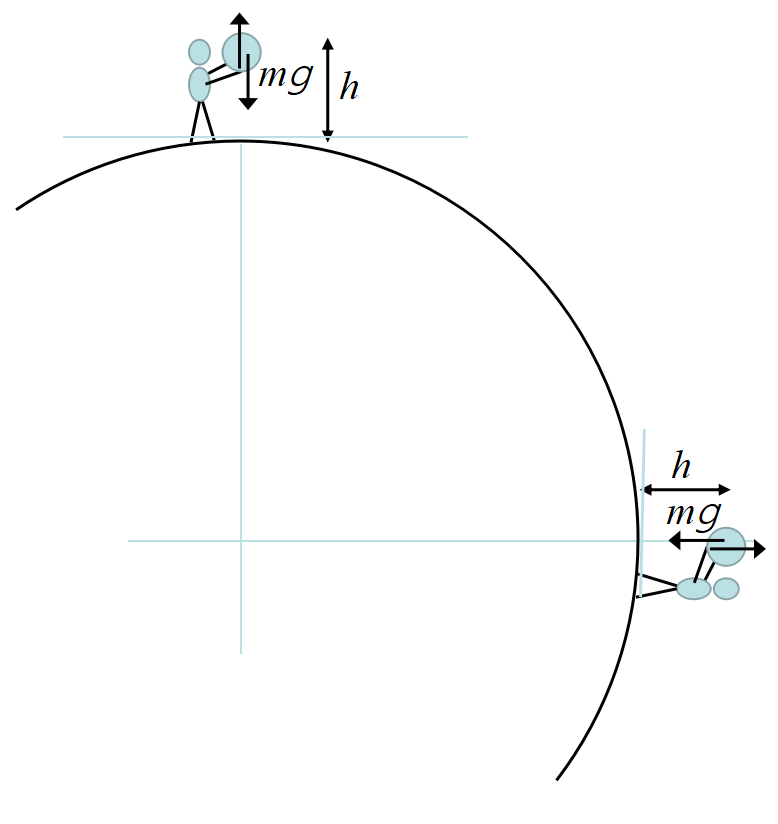
さて, 最も簡単な\(-mg~\)発生装置は地表の重力だろう。図の北極の位置で, 外力が質量\(~m~\)の物体を
\(~h~\)だけ, 静かに持ち上げる。外力は重りに\(~mgh~\)のエネルギー(力×距離)を与える。何度も習った重力位置エネルギーである。この時地球は\(-mgh~\)のエネルギーを重りに与えるので重りにエネルギーは蓄えられない。すなわち重りという「
質量」にはエネルギーは蓄えられない。
幼い頃からの経験で, 上に持ち上げた物は必ず落ちてくる。自然に落ちてくるのだから, どこにエネルギーが蓄えられるかと問われても, 困る人が大半であろう。
では, 赤道で同じことをしたらどうなるか?ばねの所で説明したように, 外力が加えたエネルギー\(~mgh~\)は\(-mg~\)発生装置に蓄えられるであろう。赤道では\(-mg~\)発生装置はただの空気である。さあ困った。エネルギーは, 目にも見えない, 何の変化も見られない空間「
重力場」に蓄えられるとしか考えざるを得ない。ばねの方がずっと分かり易い。
電場に蓄えられるエネルギー・静電エネルギー
分かり易いばねの話がまた分かり難くなってしまった!
ばねは僅かな原子の動きを拡大する装置である。構成する原子間の距離が伸縮によってばねは変形する。
では伸縮する原子のどこにエネルギーが蓄えられるのであろうか? 結晶の結合エネルギーは大まかに言って, 電気的なクーロン力と原子が近づいた時の反発力(ボルン反発力)の和で表されるが, ここではクーロン力に限って話を進めていこう。
コンデンサーの静電エネルギー・エネルギー密度
分かり易い平行板コンデンサーから。先ずは高校物理の復習。
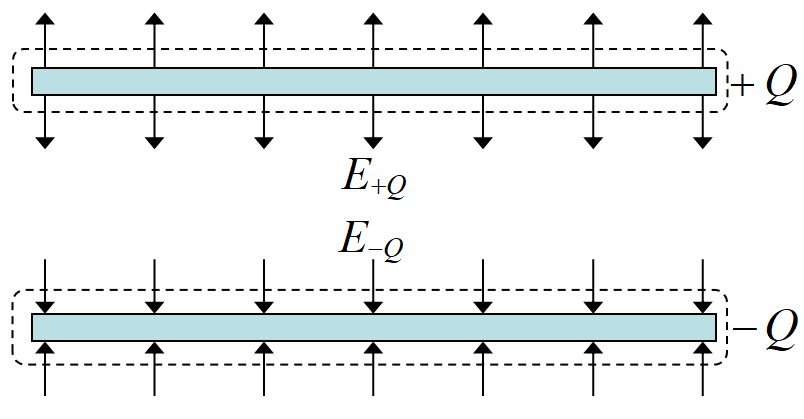
面積\(~S~\), 間隔\(~d~\)の極板に\(~+Q~\),\(~-Q~\), の電荷が分布しているコンデンサーを考える。
電気力線は極板の上下に出ているから, ガウスの法則を適用する場合, 面積は\(~S~\)ではなく\(~2S~\)である。
\[E_{+Q}\x 2S= \frac{Q}{\varepsilon_0} \]
すなわち
\[E_{+Q}= \frac{Q}{2 \varepsilon_0 S} \]
電荷\(~-Q~\)も同様の電場を生成するから, 中央部の電場は,
\[E=E_{+Q}+E_{-Q}= \frac{Q}{\varepsilon_0 S} \]
電極外部(図の上下)では, 電場\(~E_{+Q}, E_{-Q}~\)が打ち消しあい0(ゼロ)となる。極板間の電位差を\(~V~\)とすると\(~V=Ed\)から
\[\begin{align}
V&= \frac{d}{\varepsilon_0 S} Q \\
Q&= \frac{\varepsilon_0 S}{d} V \\
C&= \frac{\varepsilon_0 S}{d}
\end{align}\]
と, 高校物理でお馴染みの式となる。高校物理では\(\varepsilon_0 \to \frac{1}{4 \pi k_0}\)の方が普通か?
デジカメのフラッシュは, 内蔵コンデンサーの電荷を一気に放電して光らせる。充電したコンデンサーにはエネルギーが蓄えられている。
では, 充電したコンデンサーのエネルギーはどれくらいであろうか?
算出法は①正負の電荷を無限遠から運んでくる ②負電荷を正極板から負極板へ運ぶ方法がある。ここでは②の方でやってみよう。
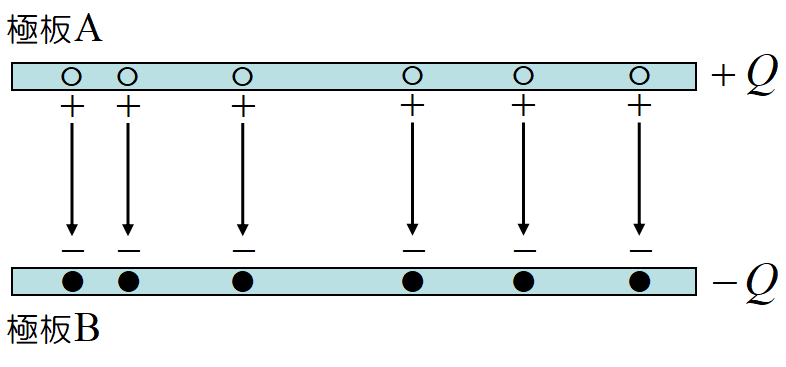
極板Aから負電荷を運び出し, 極板Bに移す。すると極板Aは正に, 極板Bは負に帯電し, またそれぞれの正, 負の電荷の大きさは等しい。極板A,Bに電荷がないときは, 電荷を運ぶ仕事はゼロであるが, 極板に電荷が貯まり始めると,負電荷は極板Aの正電荷から引力を受け, 極板Bからは斥力を受ける。従って負電荷を運ぶエネルギーは極板に貯まる電荷, すなわち極板の電位差が大きくなるほど大きくなる。
電荷の移動によって極板間の電位が変化する。微小電荷\(~\triangle q~\)を移動させている間は電位は一定と考えて良い。
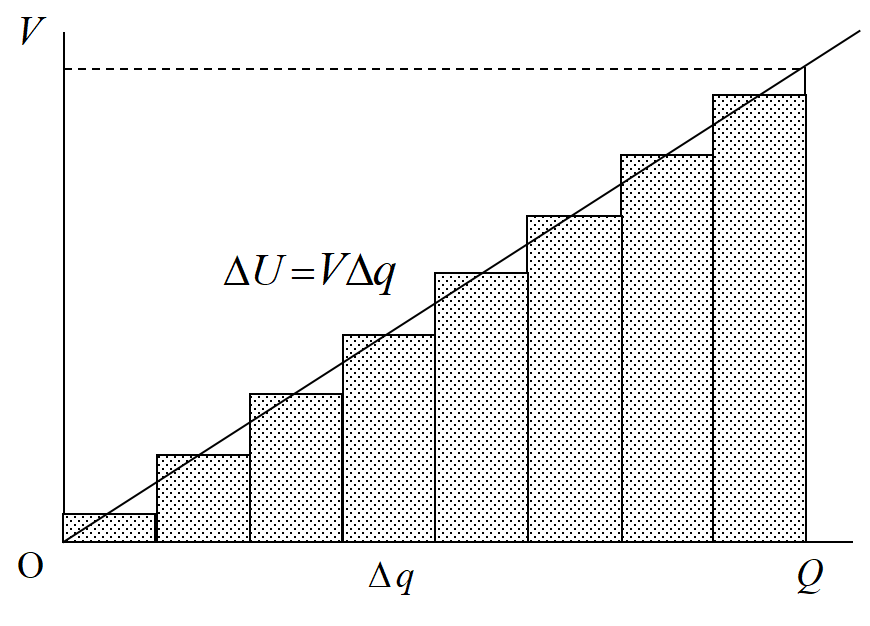
この時電荷\(~\triangle q~\)に与えるエネルギー(このエネルギーは通常電池によって与えられる)は\(~V \triangle q~\)である。これがコンデンサーのエネルギーを計算するとき\(~V-Q~\)図で\(~q~\)で積分する理由である。また\(~-Q~\)の計算が不要な理由も明らかであろう。
さてコンデンサーの場合\(~V-Q~\)は簡単で, \(~Q=CV~\)である。電荷\(~0~\)から合計\(~Q~\)の電荷を運ぶのに必要なエネルギーは
\[\begin{align}
U &= \int_{0}^{Q} V dq \\
&= \int_{0}^{Q} \frac{1}{C}Qdq \\
&= \frac{1}{2}\cdot \frac{Q^{2}}{C} = \frac{1}{2}QV= \frac{1}{2}CV^{2} \\
\end{align}\]
コンデンサーの体積は\(~S\x d~\)だから, 単位体積当たりのエネルギー, エネルギー密度は\(~V=Ed,C=\varepsilon_0 S/d~\)を使って
\[u_E= \frac{U}{Sd}= \frac{CV^{2}}{2Sd}=\frac{\varepsilon_0 S}{d}\cdot(Ed)^2\cdot\frac{1}{2Sd} =\frac{1}{2} \varepsilon_0 E^2 \tag{1} \]
と表せる。コンデンサーなので何となくそんな気もするが, 孤立電荷の作る電場にも当てはまるだろうか?
ところで頻繁に出てくる\(~\varepsilon_o\)であるが, \(~1/4 \pi \varepsilon_0 = 10^{-7}\x c^2 \)と定義された量である。よく\(~\varepsilon_o~\)の実測値というが, 光速の実測値である。また真空の誘電率というが, 真空は何も無いのであるから, 一定の電位差で電荷をより多く貯める誘電作用は当然無い。
孤立電荷の静電エネルギー・エネルギー密度
バネの中にコンデンサーが入っているわけじゃない!
ここから現実に近い孤立電荷で静電エネルギー, エネルギー密度を考えてみよう。
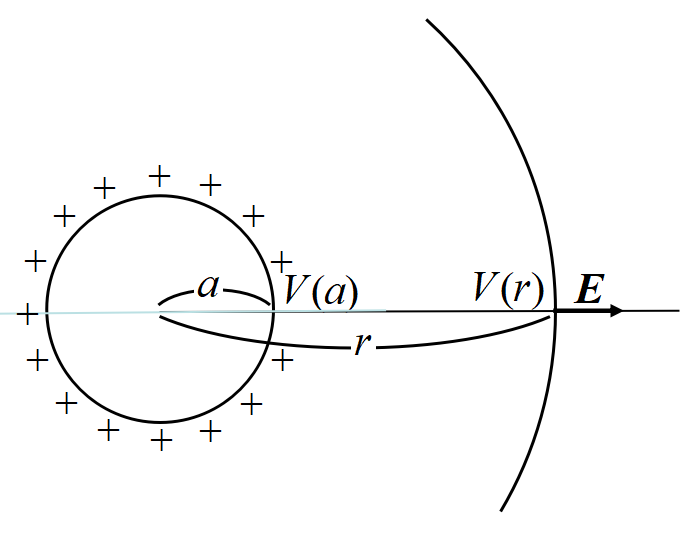
面密度\(~\sigma\)で帯電した, 半径\(~a~\)の導体球の表面電位を求める。
先ず, 半径\(~r~\)の球面での電場\(~E~\)はガウスの法則より, \(Q=4\pi a^{2}\sigma\)とすると
\[\begin{align}
E(r)\x 4\pi r^2 &= \frac{Q}{\varepsilon_0} \\
E(r) &= \frac{Q}{4 \pi \varepsilon_0 r^2} \tag{2}
\end{align}\]
となるが, これは点電荷\(~Q~\)が\(~r~\)の位置に作る電場と同じである。ならば導体球ではなく, 点電荷\(~Q~\)を用いれば良さそうであるが, 点電荷では積分が上手く出来ないという事情がある。式(6), (8)参照。
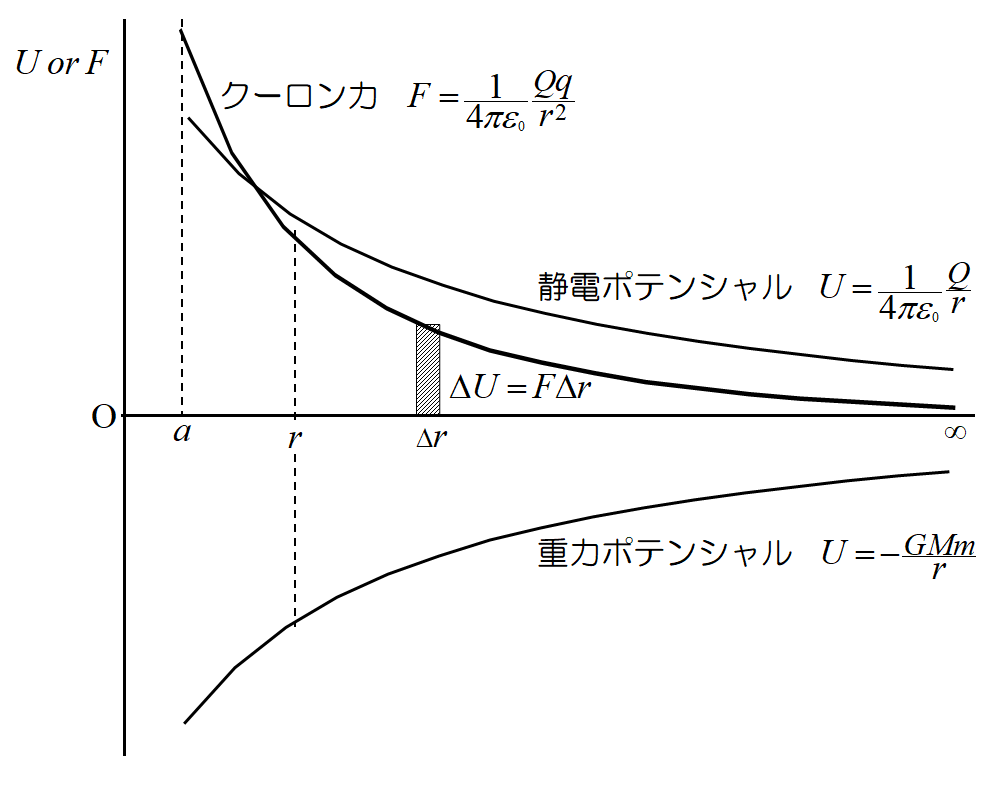
下図のクーロン力, 静電ポテンシャルは, 元々単位が異なり同一図には描けないが, 変化の傾向は分かるだろう。重力ポテンシャルにー(マイナス)がつくのが納得できない人が多い。自然は, エネルギーの高い方から低い方へ状態が変化するようになっており, 何もしなければ\(~+q~\)の電荷は遠ざかり, 彗星のかけらは太陽に引き寄せられる。無限遠を基準とすれば, 重力ポテンシャルは下図の様にー(マイナス)を付けなければならない。
電荷\(~q~\)を無限遠から距離\(~r~\)だけ離れた点に持ってくるのに要するエネルギー(クーロン力×距離)は移動方向と力の向きが逆であるから,
\[U(r)= \int_{\infty}^{r} - \frac{1}{4 \pi \varepsilon_0} \frac{Qq}{r^2}dr
= \frac{1}{4 \pi \varepsilon_0}\left[\frac{1}{r}\right]^r_\infty
= \frac{1}{4 \pi \varepsilon_0}\frac{Qq}{r} \tag{3} \]
電位とは探り電荷\(~q=+1[c]~\)のエネルギーだから, 導体球の表面電位は(2)式で\(~q=1, r=a~\)とおいて,
\[~V(a)= \frac{1}{4\pi \varepsilon_0} \frac{Q}{a} \tag{4} \]
となる。すなわち電位\(~V(a)~\)は, 表面に貯まった電荷に比例する。
(4)式は\(~C= 4\pi \varepsilon_0 a~ \)とおいて
\[Q= CV(a) \]
とする方が見慣れているかもしれない。平行板コンデンサーの結果をそのまま使って良いかの議論はあるが, コンデンサーでの考察
\[~\displaystyle U_E=\frac{1}{2} \frac{Q^2}{C}\]
により, この時導体球のエネルギーは\(~C= 4\pi \varepsilon_0 a~ \)を使って
\[U_E=\frac{1}{2} \frac{Q^2}{4 \pi \varepsilon_0 a} \tag{5} \]
となる。
電荷\(~q~\)を電場に逆らって近づける, すなわちエネルギーを加え\(~q~\)を加えて\(~Q~\)を増加させると, (3)式によって, 電位が上昇する。また(5)式によって電場のエネルギーが増えると言っても良い。目には見えないが, ばねが変形する時は, 静電場の値が変化する。つまりバネの弾性力位置エネルギーは静電場に蓄えられると考えられる。
導体球のエネルギー・正統的な方法
半径\(~a~\)の導体球に無限の彼方から無限小の電荷を少しづつ運んできて, 電荷を\(~0~\)から\(~Q~\)まで帯電させるのに必要なエネルギーは
\[\begin{align}
U_E&=\int_{0}^{Q}\int_{a}^{\infty} \frac{q\cdot dq}{4\pi \varepsilon_0 r^2}\,dr \\
&=\int_{0}^{Q}\frac{q\cdot dq}{4\pi \varepsilon_0}\left[-\frac{1}{r}\right]^\infty_a \tag{6} \\
&=\int_{0}^{Q}\frac{q}{4\pi \varepsilon_0 a}\cdot dq \\
&=\frac{1}{4\pi \varepsilon_0 a}\left[-\frac{1}{2}q^2\right]^0_Q \\
&=\frac{1}{2}\frac{Q^2}{4 \pi \varepsilon_0 a} \tag{7}\\
\end{align}\]
となり, 同じ結果を得る。(重積分については
重積分を参照)
孤立電荷の作る電場のエネルギー密度
式(1)より, 総電荷\(~Q~\)を持つ, 半径\(~a~\)の導体球で, 半径\(~r~\)の球面の電場は
\[ E(r)= \frac{1}{4 \pi \varepsilon_0}\frac{Q}{r^2} \]
であった。厚さ\(~dr~\)の球殻部分のエネルギーは
\[dU= \frac{1}{2}\varepsilon_0 E(r)^2 \x 4\pi r^2 dr \]
だから, この電場の総エネルギーは
\[\begin{align}
U_E&=\int_{a}^{\infty} \left\{\frac{1}{2}\varepsilon_0 E(r)^2 \right\}4\pi r^2dr \\
&=\int_{a}^{\infty} \frac{1}{2}\varepsilon_0 \left(\frac{1}{4\pi \varepsilon_0} \right)^2 \frac{Q^2}{r^4} 4\pi r^2dr \\
&=\frac{1}{2}\frac{Q^2}{4 \pi \varepsilon_0}\int_{a}^{\infty} \frac{1}{r^2}dr \\
&=\frac{1}{2}\frac{Q^2}{4 \pi \varepsilon_0}\left[-\frac{1}{r}\right]^\infty_a \tag{8} \\
&=\frac{1}{2}\frac{Q^2}{4 \pi \varepsilon_0 a} \\
\end{align}\]
となる。コンデンサーの結果を適用した簡易解(5), 正統的な解(7)と同じ結果が得られる。
導体球の回りには表面\(~r=a~\)から無限遠の彼方まで,
\[u_e= \frac{1}{2}\varepsilon_0 E(r)^2 \]
のエネルギー密度を有する空間が広がっていると考えて良い。
クーロン力による位置エネルギーはエネルギー密度\(\frac{1}{2}\varepsilon_0 E^2 \)の電場の中に, 蓄えられると考えて良さそうである。
遠隔作用と近接作用
クーロンの法則
\[F=k_0 \frac{q_1q_2}{r^2}\]
は, 力が瞬時に伝わる遠隔作用である。電場ベクトル
\[\Vec E= \frac{1}{4 \pi \varepsilon_0} \frac{Q}{r^2} \bm{e}_r \]
になると, 少し近接作用の感じがしてくるが, 今一歩である。そして全エネルギー。
\[\begin{align}
U_E&=\int_{0}^{Q}\int_{a}^{\infty} \frac{q\cdot dq}{4\pi \varepsilon_0 r^2}\,dr \\
&=\int_{a}^{\infty} \left\{\frac{1}{2}\varepsilon_0 E(r)^2 \right\}4\pi r^2dr\\
&=\frac{1}{2}\frac{Q^2}{4 \pi \varepsilon_0 a}
\end{align}\]
クーロンの法則の場合, 電荷の間の空間には何も無い。電場ベクトルは, そこに電場があるということで, 少し近接作用に近づく。最後の式は, 電荷の回りの空間にはエネルギーが満ち満ちているという事であり, これはもう正に近接作用だろう!!