\(u=1-x\) \(,\ \)\(\frac{du}{dx}=-1\) \( ,\ \)\(dx=-du\)
\(x=1-u\) \(,\ \)\([x=0 \to 1]\) ⇔ \([u=1 \to 0 ]\)
\(B(p,q)=\int_0^{1} x^\color{red}{{p-1}}(1-x)^\color{blue}{{q-1}}dx\) \(=\int_1^{0} (1-u)^{p-1}(1-(1-u))^{q-1}(-1)du\)
積分領域順序を換えると：
\(=\int_0^{1} (1-u)^{p-1}u^{q-1}du\)
ベータ関数の p とq の位置に注目
\(\therefore B(p,q)\)\(=\int_0^{1} u^\color{blue}{{q-1}} (1-u)^\color{red}{{p-1}}du\)\(=B(q,p)\)

\(x=sin^2θ\)\(,\ \) \(\frac{dx}{dθ}=2sinθcosθ\) \(,\ \) \(dx=2sinθcosθdθ\)
\([x=0 \to 1]\)⇔\([θ=0 \to \frac{\pi}{2}]\)
\(B(p,q)=\int_0^{1} x^{p-1}(1-x)^{q-1}dx\)
\(=\int_0^{\frac{\pi}{2}} (sin^2 θ)^{p-1}\color{red}{(1-sin^2 θ)}^{q-1} 2sinθcosθ dθ\) \(=2\int_0^{\frac{\pi}{2}} [(sin^2 θ)^{p-1}sinθ] \ [(cos^2 θ)^{q-1} cosθ] dθ\)
\((1-sin^2 θ)=cos^2θ\)
\(\therefore B(p,q)=2\int_0^{\frac{\pi}{2}} (sinθ)^{2p-1} (cosθ)^{2q-1} dθ\)

\(Γ(p)=\int_0^{\infty}e^{-x}x^{p-1}dx\)
これまでガンマ関数の変数は\(t\)でしたが、ここではp,q です。
\(x=u^2\) \(,\ \) \(\frac{dx}{du}=2u\) \( ,\ \) \(dx=2udu\)
\([x=0 \to \infty]\) ⇔ \([u=0 \to \infty ]\)
\(=\int_0^{\infty}e^{-u^2}(u^2)^{p-1}2udu\)\(=\ul{2\int_0^{\infty}e^{-u^2} u^{2p-1}du}\)

\(Γ(q)=\int_0^{\infty}e^{-x}x^{q-1}dx\)
\(x=v^2\) \(,\ \) \(\frac{dx}{dv}=2v\) \( ,\ \) \(dx=2vdv\)
\([x=0 \to \infty]\) ⇔ \([v=0 \to \infty ]\)
\(=\int_0^{\infty}e^{-v^2}(v^2)^{q-1}2vdv\)\(=\ul{2\int_0^{\infty}e^{-v^2} v^{2q-1}dv}\)

\(e\)の指数に注目すると、極座標変換が使えて、積分が簡単になる。
\(uv座標\to rθ 極座標\) \(,\)\( \ u^2+v^2=r^2\)
\(u=rcosθ\)\(,\) \(v=rsinθ\) \(,\) \(dudv=Jdrdθ=rdrdθ\):(ヤコビアンJ=r)
\([u,v:0\to\infty]\) ⇔\([r:0\to\infty \quad θ:0\to\frac{\pi}{2}]\)

上記と以下の式を比較する。
\(Γ(p)=2\int_0^{\infty}e^{-u^2} u^{2p-1}du\) \(,\) \(B(p,q)=2 \int_0^{\frac{\pi}{2}} (sinθ)^{2p-1} (cosθ)^{2q-1} dθ\)

\(=\int_0^{1} (\frac{1}{p}x^p)'(1-x)^{q}dx\)
\(=[\frac{1}{p}x^p (1-x)^{q}]_0^1\)\(-\int_0^{1} \frac{1}{p}x^p (-1)q(1-x)^{q-1}dx\) \(=0+\frac{q}{p}\int_0^{1} x^p (1-x)^{q-1}dx\) \(=\frac{q}{p}\int_0^{1} x^p (1-x)^{q-1}dx\)
定義式と比較して：
\(=\dsfr{q}{p} B(p+1,q)\)

従い
\(B(p,q+1)\)\(=\dsfr{q}{p} B(p+1,q)\)\(:❺\)
左辺を右辺替えると
\(B(p+1,q)\)\(=\dsfr{p}{q} B(p,q+1)\)\(:❺'\)

\(=\frac{p}{q} \int \{ x^{p-1}(1-x)^{q-1}-x^{p}(1-x)^{q-1}\} dx\) \(=\frac{p}{q} \int x^{p-1}(1-x)^{q-1}dx -\int x^{p}(1-x)^{q-1}dx\) \(=\frac{p}{q}\{\int_0^1 x^{p-1}(1-x)^{q-1}dx -\int_0^1 x^{p}(1-x)^{q-1}dx\}\) \(=\frac{p}{q}B(p,q)-\frac{p}{q}B(p+1,q)\)

\(B(p+1,q)=\frac{p}{q}B(p,q)-\frac{p}{q}B(p+1,q)\)

\(B(p,q)=\int_0^{1} \ul{x^{p-1}(1-x)^{q-1}}dx\)--定義式
\(=\int_0^{1} (\frac{1}{p}x^p)'　(1-x)^{q-1}dx\)
\(= [(\frac{1}{p}x^p)(1-x)^{q-1}]_0^1\)\(- \int_0^{1} \frac{1}{p}x^{p} ((1-x)^{q-1})' dx\) \(=0+\frac{q-1}{p} \int_0^{1} \ul{x^{p} (1-x)^{q-2}} dx\)
\(\therefore B(p,q)=\frac{q-1}{p}\ul{B(p+1,q-1)}\)

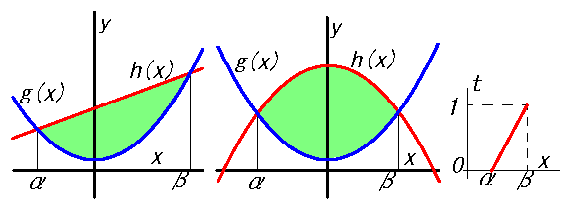
上図の右側で\(h\) が放物線 \(h=bx^2+dx+f\)のときは：
\(S=\int_α^β f(x)dx\) \(=\ul{|(b-a)|\int_α^β (x-α)(x-β)dx}　©' \)

\(S=\int_α^β f(x)dx\) \(=\int_α^β -a(x-α)(x-β)dx\) \(=-a\int_α^β (x-α)\{(x-α)＋(α-β)\}dx\) \(=-a\int_α^β \{(x-α)^2＋(α-β)(x-α)\}dx\) \(=-a [\frac{1}{3}(x-α)^3]_α^β -(β-α)\frac{1}{2}[(x-α)^2]_α^β\) \(= a\{-\frac{1}{3}(β-α)^3+\frac{1}{2}(β-α)^3\} \)
\(\therefore S=\frac{1}{6}|a|(β-α)^3\) \(:❾\)

上図の右側で\(h\) が放物線\(h=bx^2+dx+f\)のときは：
\(\therefore S=\frac{1}{6}|(b-a)|(β-α)^3\) \(:❾\)