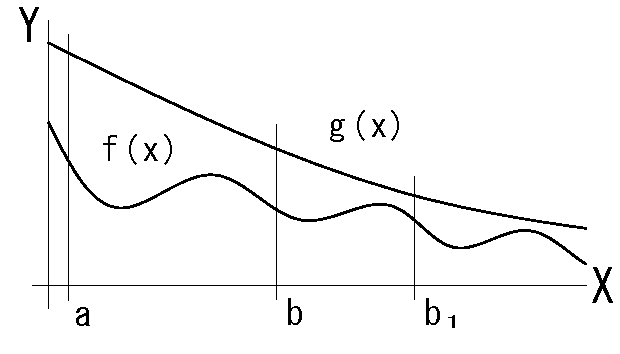広義積分 定義1
(1)
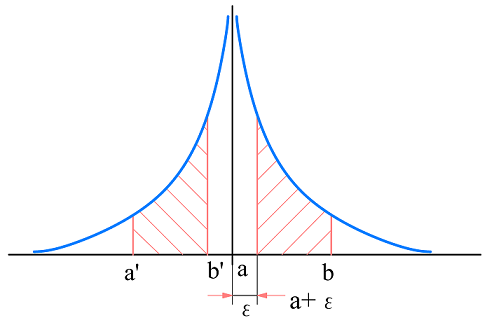
関数\(f(x)\) が半開区間 \((a,b]\) で連続、a では連続でない場合:
(図 fig1 右側参照 ):
点a に近い小さな 正の数 \(ε\)を設けて次の積分を考える。
\( \int_\color{red}{{a+ε}}^b f(x) dx \)
この定積分は成立します。
(∵\([a+ε,b]\)で連続)
そして次式の極限を考える。(積分範囲の\(ε\) を動かして極限をとる)
\( \displaystyle \lim_{ \color{red}{ε \to 0 }}\)\(\int_\color{red}{{a+ε}}^b f(x) dx \)
が存在するとき、その極限値を広義積分:
\( \int_a^b f(x) dx \)
と定義する。
(図 fig1 左側参照 ):
上記(1)と同様に
\( \displaystyle \lim_{ ε \to 0 }\)\(\int_{a'}^{{b'}-ε} f(x) dx \)
が存在するとき、その極限値を広義積分:
\( \int_{a'}^{b'} f(x) dx \)
と定義する。
|
例題1
次の広義積分の存在と値を求めよ。
\( \int_{0}^1 \frac{1}{\sqrt{x}} dx \)
(fig1の右側を参照)
\( \displaystyle \lim_{ ε \to 0 }\)\( \int_{0+ε}^1 \frac{1}{\sqrt{x}} dx \)
\(=\displaystyle \lim_{ ε \to 0 }\)\( \int_{0+ε}^1 x^{-\frac{1}{2}} dx \)
\(= \displaystyle \lim_{ ε \to 0 } \left[ 2\sqrt{x} \right]_{0+ε}^1\)
\(= \displaystyle \lim_{ ε \to 0 } 2( \left[ \sqrt{1}\right]-\left[\sqrt{0+ε} \right] ) \)\(=2\)
従って広義積分が存在し、その値は「2」 である。
次の広義積分の存在と値を求めよ。
\(\int_{-1}^0 \frac{1}{\sqrt{-x}} dx \)
(fig1の左側を参照)
\( \displaystyle \lim_{ ε \to 0 }\)\( \int_{-1}^{0-ε} \frac{1}{\sqrt{-x}} dx \)
\(= \displaystyle \lim_{ ε \to 0 } \left[-2\sqrt{-x} \right]_{-1}^{-ε}\)
\(= \displaystyle \lim_{ ε \to 0 } -2( \left[\sqrt{-ε}\right]-\left[\sqrt{1}\right] ) \)\(=2\)
2.広義積分Ⅱ
(無限区間の広義積分)
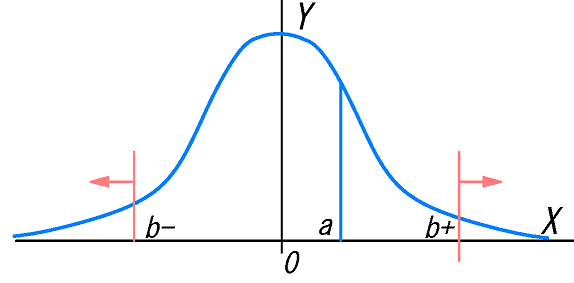
こんどは積分区分が \([a,∞)\) などの無限区間となるときの積分を考えます。
今、下図(右側)の積分区分\([a,b+]\)については積分可能とします。
次に\(a\) を固定して、\(b+\) を\(∞\) に動かし、このときの積分を次に表します。
\(\displaystyle \lim_{ b+ \to \infty }\)\( \int_{a}^{b+} f(x) dx \)
以下に積分区間が無限区間になる広義積分を定義します。
例題3
次の広義積分の存在と値を求めよ。
\( \int_{1}^{\infty} \frac{1}{x^2} dx \)
\(\displaystyle \lim_{ b \to \infty }\)\( \int_{1}^{b} \frac{1}{x^2} dx \)
\(=\displaystyle \lim_{ b \to \infty }\)\( \left[-\frac{1}{x} \right]_{1}^{b} \)
\(=\displaystyle \lim_{ b \to \infty } \left[-\frac{1}{b}+ \frac{1}{1} \right]\)
\(=[-0+1]=1\)
次の広義積分の存在と値を求めよ。
\( \int_{0}^{\infty} \frac{1}{e^x} dx \)
\(\displaystyle \lim_{ b \to \infty }\)\( \int_{0}^{b} \frac{1}{e^x} dx \)
\(=\displaystyle \lim_{ b \to \infty } -\left[ e^{-x} \right]_{0}^{b} \)
\(=\displaystyle \lim_{ b \to \infty } \left[ e^{-b}-e^{-0} \right] \)
\(=-[0-1]=1\)
(この結果は知っておくと便利)
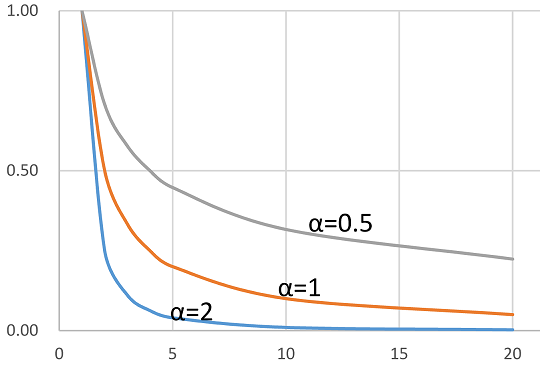
次の形の広義積分の存在が「有理式のべき乗の指数
\(α\)」によりどうなるかを調べよ。
\( \int_a^b \frac{1}{x^\color{red}{α}} dx\)
以下の結果より、計算しなくても広義積分の可否が分ります。
1)被積分関数が積分区間の下端で不連続の場合:
2)被積分関数は同上だが、積分区間の上端が無限大の場合:
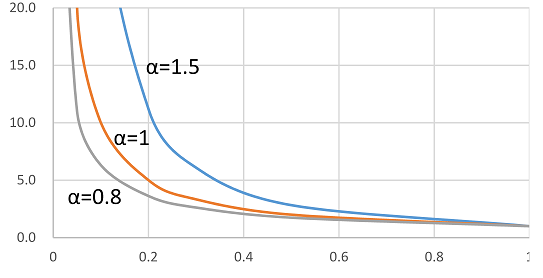
fig4 積分区間の上端が無限大
次に以下の広義積分を求めます>
\( \int_1^\infty \frac{1}{x^α} dx\)
前項と同様に「有理式のべき乗の指数\(α\)」によりどうなるかを調べます。
(a)\(α=1\) のとき:
\(\displaystyle \lim_{ b \to \infty }\)\( \int_{1}^b \frac{1}{x} dx \)
\(=\displaystyle \lim_{ b\to \infty } [ log |x|]_1^b \)
\(=\displaystyle \lim_{ b \to \infty } [logb- log 1] \)
\(=[\infty-0)]\)\(=\infty\)
\(\displaystyle \lim_{ b \to \infty }\)\( \int_{1}^b \frac{1}{x^α} dx \)
\(=\displaystyle \lim_{ b \to \infty } \frac{1}{1-α} \left[ x^{1-α} \right]_1^b \)
\(=\frac{1}{1-α} \displaystyle \lim_{ b \to \infty } \left( b^{1-α}- 1\right) \)
\(α\)により2通りの結果を得る
\(α>1 \color{red}{\rightarrow -\frac{1}{1-α}} \)
\(,\ \)\(0<α<1 \color{red}{ \rightarrow \infty } \)
結果をまとめると:
\(
\begin{cases}
-\dsfr{1}{1-α} & ( α>1 ) \\
\infty & ( 0<α ≤1 )
\end{cases}
\)
すなわち広義積分は:
\(
\begin{cases}
\color{red}{存在する} & (\color{red}{α>1} ) \\
\color{red}{存在しない} & (\color{red}{0<α ≤1} )
\end{cases}
\)
次の広義積分の存在と値を求めよ。(例題5の確認)
\( \int_{0}^1 \frac{1}{x} dx \)
\( \displaystyle \lim_{ ε \to 0 }\)\( \int_{0+ε}^1 \frac{1}{x} dx \)
\(=\displaystyle \lim_{ ε \to 0 } [log x]_ε^1\)
\(=\displaystyle \lim_{ ε \to 0 } [log1-log ε]\)\(=\infty\)
これより広義積分は存在しない。
次の広義積分の存在と値を求めよ。(例題5の確認)
\( \int_{1}^{\infty} \frac{1}{x} dx \)
\(\displaystyle \lim_{ b \to \infty }\)\( \int_{1}^{b} \frac{1}{x} dx \)
\(=\displaystyle \lim_{ b \to \infty } \left[log x \right]_{1}^{b} \)
\(=\displaystyle \lim_{ b \to \infty } \left[log b \right]\)\(=\infty\)
これより広義積分は存在しない。
例題8
次の広義積分の存在と値を求めよ。
\( \int_{0}^{\infty} \frac{x^n}{e^x} dx \)
部分積分を使い解く。【参照先】
積分しやすくなるように、つぎのいずれかの式をつかう
\( \int\ f'\ g \ dx\) \(= f\ g \ - \int \ f\ g'\ dx \)
\( \int \ f\ g'\ dx\) \(= f\ g \ - \int\ f'\ g \ dx \)
与式=
\(\displaystyle \lim_{ b \to \infty }\)\(\color{blue}{\int_{0}^{b}e^{-x}x^n dx}\)
\(f=e^{-x}, \quad g=x^n\)とおくと\(x^n\)の次数が減るので都合がよい。
\(\int_{0}^{b}e^{-x}x^n dx\)\(=\int_{0}^{b}(-e^{-x})' x^n dx\)
\(=[-e^{-x}x^n]_0^b-\int_{0}^{b}-e^{-x}x^{n-1}dx \)
\(\displaystyle \lim_{ b \to \infty }[-e^{-x} x^n]_0^b=0\)
ここで与式を \(I_n=\int_{0}^{\infty}e^{-x}x^n dx\)とおくと
\(\to I_{n-1}=\int_{0}^{\infty}e^{-x}x^{n-1} dx\)となる。
=\(\displaystyle\lim_{ b \to \infty }[-e^{-x}x^n]_0^b\)\(-\int_{0}^{b}(-e^{-x})n x^{n-1}dx \)
\(=0+n\int_{0}^{b}e^{-x}x^{n-1}dx\)
\(=n\underline{\int_{0}^{b}e^{-x}x^{n-1}dx}\)\(=n \underline{I_{n-1}}\)
同様にして
\(I_{n-1}=(n-1)I_{n-2}\), \(\ I_{n-2}=(n-2)I_{n-3}\) \( \cdots\) \(2I_1, \ 1I_0\)
\(I_0=\int_{0}^{\infty}e^{-x}x^0 dx\)
\(=\displaystyle\lim_{ b \to \infty }\) \(\int_{0}^{\infty}e^{-x}x^0 dx\)
\(=\displaystyle\lim_{ b \to \infty }\) \(\int_{0}^{\infty}e^{-x}dx\)
\(=-[e^{-x}]_0^{\infty}=1\)
これより
\( \int_{0}^{\infty} \frac{x^n}{e^x} dx \)\(=n(n-1)(n-2) \cdots 1=n!\)
(自然数の階乗となりました)
例題9不連続点のある区間の積分
次の広義積分の存在と値を求めよ。 (x=0 不連続)
\( \int_{-1}^{1} \frac{1}{\sqrt{|x|}} dx \)
・この関数はfig1 のグラフ全体
・区間の途中に不連続点がある例です。(上記3項の(1)を使う)
・例題1、2 ではこの関数を2つに分けた区間での広義積分を解いたのでした。
・2つに分けた領域は
[-1,0) と (0,1]です。
・絶対値を外して次の広義積分の式を作り解いていきます。
x が負の領域に注意
絶対値をただ外すだけでなく図をイメージしよう!(上のfig 1 を参照)
\(\displaystyle \lim_{ε \to 0}\)\(\int_{-1}^{-ε}\frac{1}{\sqrt{-x}} dx \)
\(=\displaystyle \lim_{ε \to 0}-2[\sqrt{-x}]_{-1}^{-ε}=-2[0-1]=2\)
\(\displaystyle \lim_{0 \to ε}\) \(\int_{ε}^{1}\frac{1}{\sqrt{x}} dx \)
\(\displaystyle \lim_{0 \to ε}\) \(2[\sqrt{x}]{ε}^{1}=2[1-0]=2\)
これより広義積分は収束し。以下が成り立つ。
\( \int_{-1}^{1} \frac{1}{\sqrt{|x|}} dx \)
\(=\int_{-1}^{0}\frac{1}{\sqrt{-x}} dx \)\(+\int_{0}^{1}\frac{1}{\sqrt{x}} dx=2+2=4 \)
例題10区間\(\pm \infty \)の積分
次の広義積分の存在と値を求めよ。 (x=0 不連続)
\( \int_{-\infty}^{\infty} \frac{1}{1+x^2} dx \)
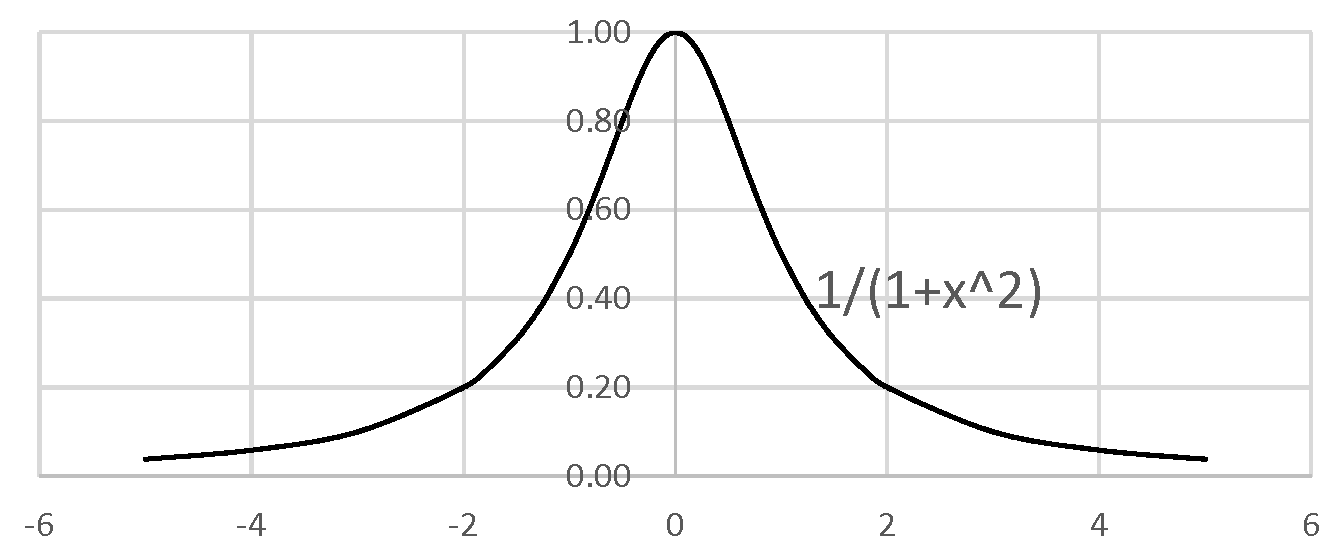
fig5 \(\frac{1}{1+x^2}\)
\( \int_{-\infty}^{\infty} \frac{1}{1+x^2} dx \)
\(=\underbrace{\int_{0}^{\infty} \frac{1}{1+x^2}dx}_{(1)} \)
\(+ \underbrace{ \int_{-\infty}^{0} \frac{1}{1+x^2}dx }_{(2)} \)
上記の(1)項と(2)項の両項が存在すれば、与式は存在(収束)します。
\((1)=\int_{0}^{\infty} \frac{1}{1+x^2} dx \)
\(=\displaystyle \lim_{a \to \infty}\)\(\int_{0}^{a} \frac{1}{1+x^2} dx \)
\(=\displaystyle \lim_{a \to \infty} [tin^{-1}x]_0^a\)
\(=\displaystyle \lim_{a \to \infty} [tin^{-1} a-tin^{-1} 0]\) \(=[\frac{\pi}{2}-0]=\frac{\pi}{2}\)
\((2)=\int_{-\infty}^{0} \frac{1}{1+x^2} dx \)
\(=\displaystyle \lim_{a \to -\infty}\)\(\int_{a}^{0} \frac{1}{1+x^2} dx \)
\(=\displaystyle \lim_{a \to -\infty} [tin^{-1}x]_a^0\)
\(=\displaystyle \lim_{a \to -\infty} [tin^{-1}0 -tin^{-1} a]\) \(=[0-(-)\frac{\pi}{2}]=\frac{\pi}{2}\)
(1)項と(2)項の存在が確認できた。⇒与式の定積分は収束し存在する。
∴\( \int_{-\infty}^{\infty} \frac{1}{1+x^2} dx=\pi \)
4.広義積分の存在
広義積分が存在(収束)する条件
今まで広義積分が解ける例題を解いてきましたが、現実は広義積分が解けることが難しいことが多い。
ここではよく使われる方法として、2つの関数 f(x)、g(x) が関わり合っているとき、一方の広義積分g(x) の収束から他の関数f(x)の収束・発散を判定する方法を説明します。
定理
比較判定法/優関数の定理
\(a\lt b\) として区間I\(=\color{fuchsia}{[a,\infty)}\)上の連続関数\(g(x),\ f(x)\) が存在し、
(区間I \(= \color{fuchsia}{ (-\infty,b],\quad [a,b),\quad (a,b] } \) についても同様です)
次の2つの条件が満たされているとき、広義積分\(\int_a^{\infty}f(x)dx\)は収束する。
ⓐ任意の\(x \in [a,\infty)\)について\(\ul{|f(x)|\le g(x)}\)が存在する
ⓑ広義積分\(\ul{\int_a^{\infty}g(x)dx}\) が収束する。
注:上記の条件を満たす\(g(x)\) を\(f(x)\) の優関数という。
|
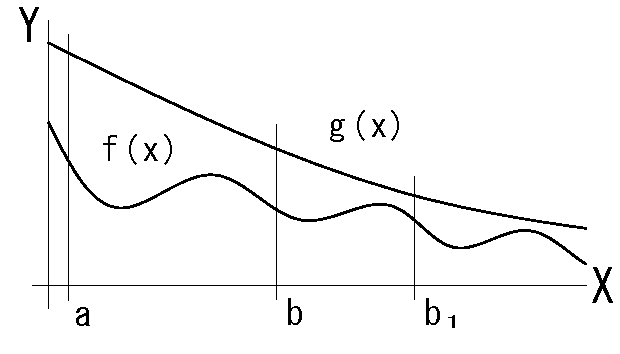
fig6 f(x)が非負
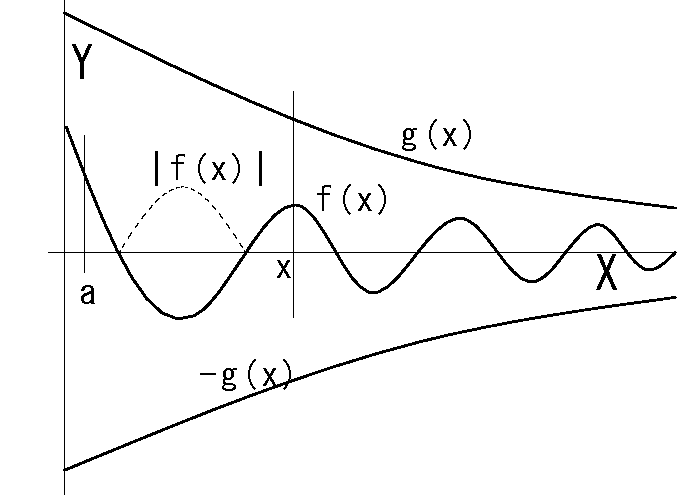
fig7 正負のとき|f(x)|
証明
ここでは
有界と単調性(「有界な単調数列は収束する」の定理)から証明します。(関数にも適用できる)
\(\color{fuchsia}{F(b),\ G(b)}\)(bは変数)の定義:
\(\displaystyle \lim_{ b \to \infty }\color{fuchsia}{F(b)}= \displaystyle \lim_{ b \to \infty }\)
\(\color{fuchsia}{\int_a^{b} f(b)dx}\)\(=\int_a^{\infty} f(x)dx\)
\(\displaystyle \lim_{ b \to \infty } \color{fuchsia}{G(b)}= \displaystyle \lim_{ b \to \infty }\)
\(\color{fuchsia}{\int_a^{b} g(b)dx}\)\(=\int_a^{\infty} g(x)dx\)
\(F(b)\)(面積)が単調増加、そして有界を示します。
1)fig 3 より変数b の増加による、面積(\(F(b)\))の単調増加は明白ですね、すなわち:
\(b_1 \lt b_2 \lt b_3 \cdots\) なら \(F(b_1) \le F(b_2) \le F(b_3) \cdots\)
これは広義単調増加です。
直感的に「関数\(F(b)\)は収束する関数\(G(b)\)に抑えられている」から有界だろうが、式で表わすと:
2)任意のb について:
\(\color{fuchsia}{F(b)}=\int_a^{b} f(b)dx\)\(\le \int_a^{b} g(b)dx\)\(=G(b)\)\(\color{fuchsia}{ \le \displaystyle \lim_{ b \to \infty } G(b)}\)
これより関数\(F(b)\)は有界です。
1)、2)より
\(\displaystyle \lim_{ b \to \infty } F(b)\)
が存在し
\(\displaystyle \lim_{ b \to \infty } F(b)\)\(=\int_a^{\infty} f(x)dx\)である。
上記\(f(x)\)が非負のときの証明ですが、\(f(x)\)は正負を含めて、上記定理のⓐでは\(\ul{|f(x)|}\le g(x)\)と
絶対値が付いています。
(以下の具体例2)を参照)
具体例
f(x)の広義積分 \(\Rightarrow\)右側が優関数g(x)とする。
1)
\(\int_1^{\infty} \frac{1}{x^2+1}dx\) \(\Rightarrow\) \(g(x)=\frac{1}{x^2}\)
\(\dsfr{1}{x^2+1}\le\dsfr{1}{x^2}\)である。
\(\int_1^{\infty} \dsfr{1}{x^2}dx=\displaystyle \lim_{b \to \infty}\)\(\ \int_1^{b} \dsfr{1}{x^2}dx\)
\(=\displaystyle\lim_{b \to \infty}\)\([-x^{-1}]_1^b\)\(==\displaystyle\lim_{b \to \infty}\)\((-b^{-1}+1^{-1})=1\)
\(\therefore \int_1^{\infty} \dsfr{1}{x^2}dx\) が収束したので与式も収束する。
2) \(\int_1^{\infty} \frac{sin x}{x^2}dx\) \(\Rightarrow\) \(g(x)=\frac{1}{x^2}\)
\(|sin x|\le 1\)であることに留意する。
\(|\frac{sin x}{x^2}| \le \frac{1}{x^2} \)
\(\frac{1}{x^2}\) の広義積分の収束は上記1) にて証明済み
3) \(\int_1^{\infty} \frac{sin x}{x^2+1}dx\) \(\Rightarrow\) \(g(x)=\frac{1}{x^2}\)
上記 1), 2)から 優関数が \(g(x)=\frac{1}{x^2}\)が明らかです。

[コーヒーブレイク/閑話]…お疲れ様でした。